| Вариант 11
1. Для проверки 7 групп студентов назначается 2 инспектора, один из которых проверяет 3 группы, а второй -4 группы. Чему равна вероятность того, что при случайном распределении групп между инспекторами ваша группа будет проверена инспектором, которому выделены три группы для проверки.
Решение:
Вероятность выигрыша можно рассчитать по формуле классической вероятности
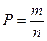 , где m – число благоприятных исходов, n – число полных исходов. , где m – число благоприятных исходов, n – число полных исходов.
Все билеты различные, значит число полных исходов определяется по формуле сочетаний:
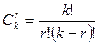 , где k=100, r=3, т.е. , где k=100, r=3, т.е.
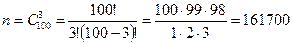 . .
2. Имеются две одинаковые урны, в одной из которых все шары белые, а в другой 2-белых и 2 черных шара. Вы подошли к одной из урн и извлекли белый шар, затем его возвратили обратно и снова наудачу извлекли шар из этой урны, и он оказался белым. Подобный опыт провели в третий раз и получили тот же результат. Определить вероятность того, что вы подошли к урне с белыми шарами.
Решение:
Задача 5
.
В одном ящике 3 белых и 5 черных шаров, в другом ящике – 6 белых и 4 черных шара. Найти вероятность того, что хотя бы из одного ящика будет вынут белый шар, если из каждого ящика вынуто по одному шару.
Решение
. Событие A={хотя бы из одного ящика вынут белый шар} можно представить в виде суммы 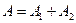 , где события , где события 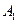 и и  означают появление белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна означают появление белого шара из первого и второго ящика соответственно. Вероятность вытащить белый шар из первого ящика равна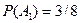 , а вероятность вытащить белый шар из второго ящика , а вероятность вытащить белый шар из второго ящика 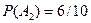 . Кроме того, в силу независимости . Кроме того, в силу независимости 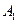 и и  имеем: имеем: 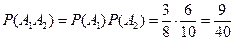 . По теореме сложения получаем: . По теореме сложения получаем:  . .
3. В розыгрыше первенства по футболу участвуют 18 команд, из которых случайным образом формируются две группы по 9 команд в каждой. Среди участников соревнований 5 команд экстра-класса. Найти вероятность того, что: а) все команды экстра-класса попадут в одну и ту же группу; б) две команды экстра-класса попадут в одну группу, а три – в другую.
Решение:
Для решения этой задачи воспользуемся формулами комбинаторики. В обоих случаях число возможных вариантов распределений 18-ти командам на 2 группы по 9 человек считается как число сочетаний без повторений:

Вычислим число благоприятных исходов, в зависимости от искомых вероятностей:
а: Нарисуем схему состава благоприятной группы:
5 мест в группе должны занимать команды экстра-класса (э), а 4 оставшихся места X займут 13 нераспределённых команд, т.е. число таких распределений будет таким: 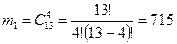 Следовательно, вероятность благоприятных исходов определяется отношением их количественного значения к количеству всех возможных исходов: Следовательно, вероятность благоприятных исходов определяется отношением их количественного значения к количеству всех возможных исходов: 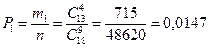
б: Нарисуем схемы состава благоприятных групп:
и
Рассмотрим первую группу. В ней 2 команды экстра-класса и 7 свободных мест, по которым и необходимо рассчитать распределение оставшихся 13-ти команд не экстра-класса: 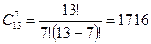 . Но на месте двух команд экстра-класса в первой группе могли бы быть каждая из 3-х, которые в другой группе, т. е. всего таких взаимных расположений может быть . Но на месте двух команд экстра-класса в первой группе могли бы быть каждая из 3-х, которые в другой группе, т. е. всего таких взаимных расположений может быть 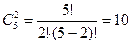 . Таким образом, число благоприятных исходов: . Таким образом, число благоприятных исходов: 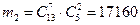 Вероятность этих исходов: Вероятность этих исходов: 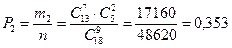
Ответ:  , ,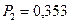 . .
4. Доходы некоторой категории семей распределены по нормальному закону со средним значением a=15000 р. И дисперсией 10000. Рассматривается часть этой категории семей, у которой доходы больше 14000 р. Найти закон распределения дохода у этой части и его среднее значение. (Определение характеристик усеченного распределения.)
Решение:
5. В ящике 20 деталей, из которых 7 деталей бракованных. Из ящика извлекается 9 деталей. Определить закон распределения числа бракованных деталей в выборке. Найти математическое ожидание и дисперсию этой случайной величины.
Решение:
Решается!!!!!!
6. Закон распределения случайного вектора (X,Y) определяется таблицей
| X
|
Y
|
| -1
|
0
|
1
|
2
|
| 1
|
0.05
|
0.10
|
0.15
|
0.10
|
| 2
|
0.05
|
0.15
|
0.15
|
0.05
|
| 3
|
0.10
|
0.05
|
0
|
0.05
|
а) Определить безусловные и условные законы распределения X и Y,
б) Определить математическое ожидание и дисперсию этих величин, а также коэффициент корреляции между ними.
Решение:
Задача 3
.
Совместный закон распределения случайных величин x и h задан c помощью таблицы
| x h
|
1
|
2
|
| –1
|
1/16
|
3/16
|
| 0
|
1/16
|
3/16
|
| 1
|
1/8
|
3/8
|
Вычислить частные законы распределения составляющих величин x и h. Определить, зависимы ли они. Вычислить вероятность 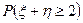 . .
Решение.
Частное распределение для x получается суммированием вероятностей в строках:
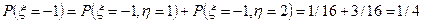 ; ;
 ; ;
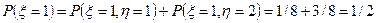 . .
Аналогично получается частное распределение для h:
 ; ;
 . .
Полученные вероятности можно записать в ту же таблицу напротив соответствующих значений случайных величин:
| x h
|
1
|
2
|
px
|
| –1
|
1/16
|
3/16
|
1/4
|
| 0
|
1/16
|
3/16
|
1/4
|
| 1
|
1/8
|
3/8
|
1/2
|
| ph
|
1/4
|
3/4
|
1
|
Теперь ответим на вопрос о независимости случайных величин x и h. С этой целью для каждой клетки совместного распределения вычислим произведение 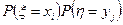 (т.е. сумм по соответствующей строке и столбцу) и сравним его со значением вероятности (т.е. сумм по соответствующей строке и столбцу) и сравним его со значением вероятности 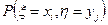 в этой клетке. Например, в клетке для значений x=-1 и h=1 стоит вероятность 1/16, а произведение соответствующих частных вероятностей 1/4×1/4 равно 1/16, т.е. совпадает с совместной вероятностью. Это условие так же проверяется в оставшихся пяти клетках, и оно оказывается верным во всех. Следовательно, случайные величины x и h независимы. в этой клетке. Например, в клетке для значений x=-1 и h=1 стоит вероятность 1/16, а произведение соответствующих частных вероятностей 1/4×1/4 равно 1/16, т.е. совпадает с совместной вероятностью. Это условие так же проверяется в оставшихся пяти клетках, и оно оказывается верным во всех. Следовательно, случайные величины x и h независимы.
Заметим, что если бы наше условие нарушалось хотя бы в одной клетке, то величины следовало бы признать зависимыми.
Задача 8
. Случайные приращения цен акций двух компаний за день x и h имеют совместное распределение, заданное таблицей:
| x h
|
-1
|
+1
|
| -1
|
0,3
|
0,2
|
| +1
|
0,1
|
0,4
|
Найти коэффициент корреляции.
Решение.
Прежде всего вычисляем Mxh=0,3-0,2-0,1+0,4=0,4. Далее находим частные законы распределения x и h:
| x h
|
-1
|
+1
|
px
|
| -1
|
0,3
|
0,2
|
0,5
|
| +1
|
0,1
|
0,4
|
0,5
|
| ph
|
0,4
|
0,6
|
|
Определяем Mx=0,5-0,5=0; Mh=0,6-0,4=0,2; Dx=1; Dh=1–0,22
=0,96; cov(x,h)=0,4. Получаем
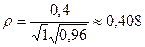 . .
7. Бла
Задача 2
.
Пусть двумерный случайный вектор (x, h) равномерно распределен внутри треугольника 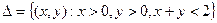 . Вычислить вероятность неравенства x>h. . Вычислить вероятность неравенства x>h.
Решение.
Площадь указанного треугольника 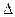 равна равна  (см. рис. 7.1). В силу определения двумерного равномерного распределения совместная плотность случайных величин x, h равна (см. рис. 7.1). В силу определения двумерного равномерного распределения совместная плотность случайных величин x, h равна
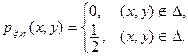
Событие 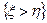 соответствует множеству соответствует множеству 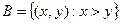 на плоскости, т.е. полуплоскости. Тогда вероятность на плоскости, т.е. полуплоскости. Тогда вероятность
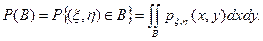

Рис. 7.1.
На полуплоскости B совместная плотность  равна нулю вне множества равна нулю вне множества 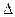 и 1/2 – внутри множества и 1/2 – внутри множества 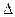 . Таким образом, полуплоскость B разбивается на два множества: . Таким образом, полуплоскость B разбивается на два множества: 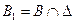 и и  . Следовательно, двойной интеграл по множеству B представляется в виде суммы интегралов по множествам . Следовательно, двойной интеграл по множеству B представляется в виде суммы интегралов по множествам  и и 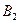 , причем второй интеграл равен нулю, так как там совместная плотность равна нулю. Поэтому , причем второй интеграл равен нулю, так как там совместная плотность равна нулю. Поэтому
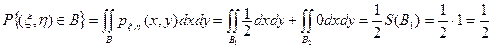 . .
Если задана совместная плотность распределения  случайной пары (x,h), то плотности случайной пары (x,h), то плотности 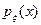 и и  составляющих x и h называются частными плотностями
и вычисляются по формулам: составляющих x и h называются частными плотностями
и вычисляются по формулам:

Для непрерывно распределенных случайных величин с плотностями рx
(х), рh
(у) независимость означает, что при любых х и у выполнено равенство
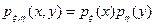 . .
8. Бла
9. Бла


10. Бла
11. Бла




|