| Задача 1. Построение и анализ однофакторной эконометрической модели
Однофакторная производственная функция накладных расходов в шахтном строительстве имеет вид
У=a0
+a1
x+e,
где У – накладные расходы, часть в затратах;
х – годовой объем затрат, тыс. грн;
На основании статистических данных по девяти шахтостроительным управлениям, используя 1МНК, найти оценки параметров производственной функции накладных расходов для шахтостроительного объединения. Дать общую характеристику достоверности и экономическую интерпритацию построенной модели.
Таблица 1 – Исходные данные
| № п\п
|
Накладные расходы
|
Объем работ
|
| 1
|
27
|
15,6
|
| 2
|
30
|
15,3
|
| 3
|
28
|
14,9
|
| 4
|
29
|
15,1
|
| 5
|
26
|
16,1
|
| 6
|
25
|
16,7
|
| 7
|
28
|
15,4
|
| 8
|
26
|
17,1
|
| 9
|
25
|
16,8
|
Построение и анализ классической однофакторной эконометрической модели
1. Спецификация модели.
1.1 Идентификация переменных
Y – накладные расходы – результирующий показатель;
Х – объем работ – показатель-фактор;
Таблица 2 – Исходные данные и элементарные превращения этих данных для оценки модели.
| № п\п
|
Накладные расходы
|
Объем работ
|
Х*X
|
Y*Y
|
ОценкаУ
|
Отклонение, е
|
Предсказанное Y
|
Остатки
|
| 1
|
27
|
15,6
|
243,36
|
729
|
27,64235
|
-0,642345002
|
27,642345
|
-0,642345
|
| 2
|
30
|
15,3
|
234,09
|
900
|
28,19401
|
1,805989034
|
28,19401097
|
1,805989
|
| 3
|
28
|
14,9
|
222,01
|
784
|
28,92957
|
-0,929565584
|
28,92956558
|
-0,9295656
|
| 4
|
29
|
15,1
|
228,01
|
841
|
28,56179
|
0,438211725
|
28,56178827
|
0,4382117
|
| 5
|
26
|
16,1
|
259,21
|
676
|
26,7229
|
-0,722901729
|
26,72290173
|
-0,7229017
|
| 6
|
25
|
16,7
|
278,89
|
625
|
25,61957
|
-0,619569802
|
25,6195698
|
-0,6195698
|
| 7
|
28
|
15,4
|
237,16
|
784
|
28,01012
|
-0,010122311
|
28,01012231
|
-0,0101223
|
| 8
|
26
|
17,1
|
292,41
|
676
|
24,88402
|
1,115984817
|
24,88401518
|
1,1159848
|
| 9
|
25
|
16,8
|
282,24
|
625
|
25,43568
|
-0,435681147
|
25,43568115
|
-0,4356811
|
| Сумма
|
244
|
143
|
2277,4
|
6640
|
244
|
0
|
244
|
0
|
| Среднее
|
27,11111111
|
15,88888889
|
253,04
|
737,78
|
27,11111
|
-
|
27,11111111
|
-
|
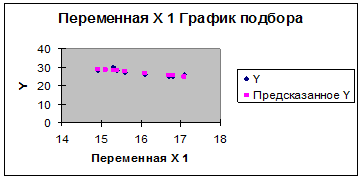
1.2 Общий вид линейной однофакторной модели и её оценки
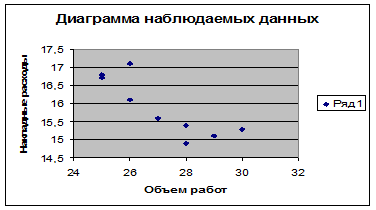
Полученная диаграмма свидетельствует о слабой обратной зависимости. Введем гипотезу, что между фактором Х и показателем У нет корреляционной зависимости.
1.3 Оценка тесноты связи между результативным показателем У и фактором Х на основании коэффициента парной корреляции
Парные коэффициенты корреляции вычисляем по формуле:
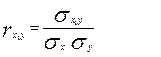
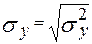 – среднее квадратическое отклонение показателя Y; – среднее квадратическое отклонение показателя Y;
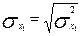 – среднее квадратическое отклонение фактора X; – среднее квадратическое отклонение фактора X;
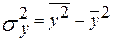 – дисперсия показателя Y; – дисперсия показателя Y;
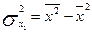 – дисперсия показателя X; – дисперсия показателя X;
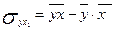 – коэффициент ковариации признаков Y и Х; – коэффициент ковариации признаков Y и Х;
| По формуле
|
Мастер функций
|
| Дисперсия Х
|
Ср. кв. отклон Х
|
Дисперсия Х
|
Ср. кв. отклон Х
|
| 0,658611111
|
0,811548588
|
0,658611111
|
0,811548588
|
| Дисперсия У
|
Ср. кв. отклон У
|
Дисперсия У
|
Ср. кв. отклон У
|
| 3,111111111
|
1,763834207
|
3,111111111
|
1,763834207
|
| Ковариация ХУ
|
Ковариация ХУ
|
| -1,07654321
|
-1,07654321
|
| rху
|
-0,8461
|
rху
|
-0,8461
|
Вывод: Поскольку коэффициент парной корреляции rху
=-0,8461, то это свидетельствует об отсутствии тесной связи между объемом работ и накладными расходами.
2. Оценка параметров модели методом 1МНК
Таблица 3 – Оценка параметров модели
| По формуле
|
Регрессия
|
| Коэффициенты
|
| 56,32897439
|
У-пересечение
|
56,32897512
|
| -1,8388865
|
Объем работ, Х
|
-1,838886546
|
Таким образом, оцененная эконометрическая модель:
у=56,32897439–1,838886546х
3. Общая характеристика достоверности модели
Для общей оценки адекватности принятой эконометрической модели данным, которые наблюдаем, воспользуемся коэффициентом множественной детерминации R2
.
Таблица 4 – Общая характеристика достоверности моделей
| По формуле
|
Регрессионная статистика
|
| R
|
-0,84608053
|
Множественный R
|
-0,84608053
|
| R2
|
0,715852263
|
R-квадрат
|
0,71585226
|
Вывод: Поскольку коэффициент множественной детерминации R2
= 0,71585226, то это свидетельствует, что вариация объема накладных расходов на 72% определяется вариацией объема работ и на 28% вариацией других факторов, которые не вошли в модель. Коэффициент корреляции R=-0,84608053 характеризует слабую связь между этими показателями. Модель не адекватна.
Задача 2. Построение и анализ многофакторной эконометрической модели
Условие задачи
По статистическим данным для 9 предприятий общественного питания за год построить линейную двухфакторную модель, которая характеризует зависимость между уровнем рентабельности (%), относительным уровнем затрат оборота (%) и трудоемкостью предприятий. Прогнозные значения факторов выбрать самостоятельно. Сделать экономический анализ характеристик взаимосвязи.
Исходные данные
| № п/п
|
Рентабельность
|
Затраты оборота
|
Трудоемкость
|
| 1
|
2,32
|
38,8
|
114
|
| 2
|
2,19
|
39,9
|
101,1
|
| 3
|
2,83
|
30,1
|
153,8
|
| 4
|
2,75
|
31,7
|
146
|
| 5
|
2,59
|
17,2
|
124,8
|
| 6
|
2,27
|
39,7
|
103,6
|
| 7
|
2,05
|
36,9
|
119
|
| 8
|
1,95
|
38,2
|
108,7
|
| 9
|
2,08
|
40,1
|
106,5
|
Построение и анализ классической многофакторной линейной эконометрической модели
1. Спецификация модели
1.1 Идентификация переменных
Многофакторная линейная эконометрическая модель устанавливает линейную зависимость между одним показателем и несколькими факторами.
Y – рентабельность – результирующий показатель;
Х1 – затраты оборота – показатель-фактор;
Х2 – трудоемкость – показатель-фактор.
Таблица 1 – Исходные данные и элементарные превращения этих данных для оценки модели
| № п/п
|
Y
|
X1
|
X2
|
Y*X1
|
Y*X2
|
X1*X2
|
Y*Y
|
X1*X1
|
X2*X2
|
| 1
|
2,32
|
38,8
|
114
|
90,016
|
264,48
|
4423
|
5,382
|
1505,44
|
12996
|
| 2
|
2,19
|
39,9
|
101,1
|
87,381
|
221,41
|
4034
|
4,796
|
1592,01
|
10221,2
|
| 3
|
2,83
|
30,1
|
153,8
|
85,183
|
435,25
|
4629
|
8,009
|
906,01
|
23654,4
|
| 4
|
2,75
|
31,7
|
146
|
87,175
|
401,5
|
4628
|
7,563
|
1004,89
|
21316
|
| 5
|
2,59
|
17,2
|
124,8
|
44,548
|
323,23
|
2147
|
6,708
|
295,84
|
15575
|
| 6
|
2,27
|
39,7
|
103,6
|
90,119
|
235,17
|
4113
|
5,153
|
1576,09
|
10733
|
| 7
|
2,05
|
36,9
|
119
|
75,645
|
243,95
|
4391
|
4,203
|
1361,61
|
14161
|
| 8
|
1,95
|
38,2
|
108,7
|
74,49
|
211,97
|
4152
|
3,803
|
1459,24
|
11815,7
|
| 9
|
2,08
|
40,1
|
106,5
|
83,408
|
221,52
|
4271
|
4,326
|
1608,01
|
11342,3
|
| ∑
|
21
|
312,6
|
1077,5
|
717,965
|
2558,5
|
36788
|
49,94
|
11309,1
|
131815
|
| Средн.
|
2,34
|
34,733
|
119,722
|
79,7739
|
284,28
|
4088
|
5,549
|
1256,57
|
14646,1
|
1.2 Оценка тесноты связи между показателем Y и факторами Х1 и Х2, а также межу факторами. (Диаграмма рассеяния)
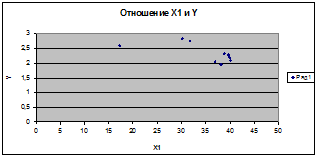
Связь обратная
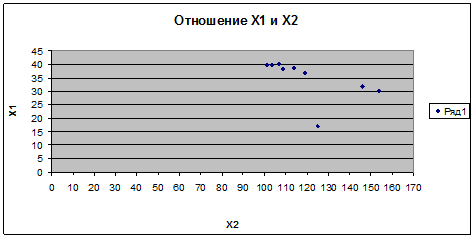
Связь обратная
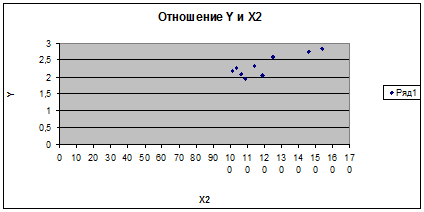
Связь тесная прямая
| Прозноз
|
| 1)
Отношение Х1 и У
|
| r
=-0,5
|
| 2)
Отношение Х1 и Х2
|
| r
=-0,4
|
| 3)
Отношение У и Х2
|
| r
=0,5
|
1.2.1 Парные коэффициенты корреляции, корреляционная матрица
Для оценки тесноты связи между показателем Y и факторами Х1 и Х2, а также между факторами вычисляем парные коэффициенты корреляции, а потом составляем корреляционную матрицу, учитывая ее особенности:
– корреляционная матрица является симметричной;
– на главной диагонали размещены единицы.
Парные коэффициенты корреляции вычисляем по формулам:
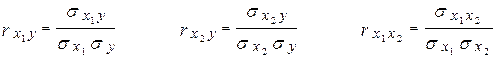
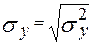 – среднее квадратическое отклонение показателя Y; – среднее квадратическое отклонение показателя Y;
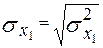 – среднее квадратическое отклонение фактора X1; – среднее квадратическое отклонение фактора X1;
 – среднее квадратическое отклонение фактора X2; – среднее квадратическое отклонение фактора X2;
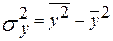 – дисперсия показателя Y; – дисперсия показателя Y;
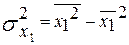 – дисперсия показателя X1; – дисперсия показателя X1;
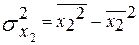 – дисперсия показателя X2; – дисперсия показателя X2;
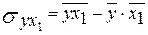 – коэффициент ковариации признаков Y и Х1; – коэффициент ковариации признаков Y и Х1;
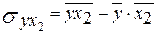 – коэффициент ковариации признаков Y и Х2; – коэффициент ковариации признаков Y и Х2;
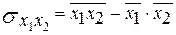 – коэффициент ковариации признаков X1 и Х2; – коэффициент ковариации признаков X1 и Х2;
Таблица 2 – Расчет парных коэффициентов корреляции
| По формуле
|
Мастер
функций
|
| Дисперсия У
|
Ср. кв. отклон У
|
Дисперсия У
|
Ср. кв. отклон У
|
| 0,089133333
|
0,298552061
|
0,089133333
|
0,298552061
|
| Дисперсия Х1
|
Ср. кв. отклон Х1
|
Дисперсия Х1
|
Ср. кв. отклон Х1
|
| 50,16666667
|
7,08284312
|
50,16666667
|
7,08284312
|
| Дисперсия Х2
|
Ср. кв. отклон Х2
|
Дисперсия Х2
|
Ср. кв. отклон Х2
|
| 312,6550617
|
17,68205479
|
312,6550617
|
17,68205479
|
| Ковариация УХ1
|
Ковариация УХ1
|
| -1,386333333
|
-1,386333333
|
| Ковариация УХ2
|
Ковариация УХ2
|
| 4,524851852
|
4,524851852
|
| Ковариация Х1Х2
|
Ковариация Х1Х2
|
| -70,76962963
|
-70,76962963
|
Коэффициенты парной корреляции
| rух1
|
-0,655601546
|
rух1
|
-0,655601546
|
| rух2
|
0,857139597
|
rух2
|
0,857139597
|
| rух1х2
|
-0,565075617
|
rух1х2
|
-0,565075617
|
| Корреляционная матрица
|
|
| 1
|
-0,655601546
|
0,857139597
|
| -0,655601546
|
1
|
-0,565075617
|
| 0,857139597
|
-0,565075617
|
1
|
1.2.2 Коэффициенты частичной корреляции
В многомерной модели коэффициенты парной корреляции измеряют нечистую связь между факторами и показателем. Поэтому при построении двухфакторной модели целесообразно оценить связь между показателем и одним фактором при условии, что влияние другого фактора не считается. Для измерения такой чистой связи вычисляют коэффициенты частичной корреляции.
Формула частичного коэффициента корреляции между признаками Хi и Xj имеет вид: имеет вид:
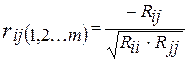
где 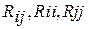 – алгебраические дополнения соответствующих элементов корреляционной матрицы. – алгебраические дополнения соответствующих элементов корреляционной матрицы.
Во время построения двухфакторной модели коэффициенты частичной корреляции рассчитываются по формулам:
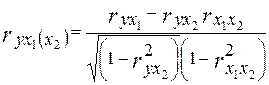
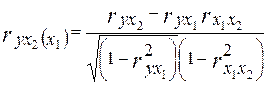
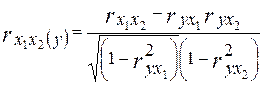
Для проверки полученных коэффициентов рассчитаем их матричным методом по формуле:
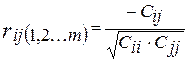
где 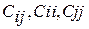 – элементы матрицы – элементы матрицы 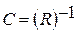 обратной корреляционной матрицы R. обратной корреляционной матрицы R.
Таблица 3 – Расчеты коэффициентов частичной корреляции
| По определению
|
Матричный метод
|
| ryx1 (x2)
|
-0,402981473
|
-0,402981473
|
| ryx2 (x1)
|
0,781189003
|
0,781189003
|
| rx1x2 (y)
|
-0,005029869
|
-0,005029869
|
| Корреляционная матрица, R
|
Матрица, обратная корреляционной, C
|
| y
|
x1
|
x2
|
| y
|
1
|
-0,655601546
|
0,857139597
|
4,499910061
|
1,13212031
|
-3,2173175
|
| x1
|
-0,655601546
|
1
|
-0,565075617
|
1,132120315
|
1,75392563
|
0,02071546
|
| x2
|
0,857139597
|
-0,565075617
|
1
|
-3,21731751
|
0,02071546
|
3,76939603
|
Значения коэффициентов, полученные двумя методами, совпали.
1.2.3 Выводы о том, являются ли факторы ведущими и возможной мультиколлнеарности
С помощью полученных корреляционной матрицы и коэффициентов частичной корреляции можно сделать выводы о значимости факторов и проверить факторы на мультиколлинеарность – линейную зависимость или сильную корреляцию.
1) Поскольку коэффициент парной корреляции между затратами оборота и рентабельностью rух1 = -0,655601546 и соответствующий коэффициент частичной корреляции ryx1 (х2) = – 0,402981473, это значит, что затраты оборота имеют обратное среднее влияние на рентабельность.
2) Поскольку коэффициент парной корреляции между трудоемкостью и рентабельностью rух2=0,857139597, а соответствующий коэффициент частичной корреляции rух2 (х1)= 0,781189003, то это свидетельствует о том, что трудоемкость существенно влияет на рентабельность.
3) Поскольку коэффициент парной корреляции между рентабельностью и затратами оборота = -0,565075617, а соответствующий коэффициент частичной корреляции rх1х2 (у) = -0,005029869 то можно сказать, что существует средняя обратная корреляционная зависимость.
3. Общий вид линейной двухфакторной модели и её оценка в матричной форме
В общем виде многофакторная линейная эконометрическая модель записывается так:
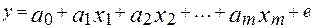
В матричной форме модель и ее оценка будут записаны в виде:
 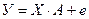 и и 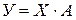 , , 
где У – вектор столбец наблюдаемых значений показателя;
У – вектор столбец оцененных значений фактора;
Х – матрица наблюдаемых значения факторов;
А – вектор столбец невидимых параметров;
А – вектор столбец оценок параметров модели;
е – вектор столбец остатков (отклонений).
| 2,32
|
1,0
|
38,8
|
114
|
| 2,19
|
1,0
|
39,9
|
101,1
|
| 2,83
|
1,0
|
30,1
|
153,8
|
| 2,75
|
1,0
|
31,7
|
146
|
| Y=
|
2,59
|
X=
|
1,0
|
17,2
|
124,8
|
| 2,27
|
1,0
|
39,7
|
103,6
|
| 2,05
|
1,0
|
36,9
|
119
|
| 1,95
|
1,0
|
38,2
|
108,7
|
| 2,08
|
1,0
|
40,1
|
106,5
|
| 1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
| Xtrans=
|
38,8
|
39,9
|
30,1
|
31,7
|
17,2
|
39,7
|
36,9
|
38,2
|
| 114,0
|
101,1
|
153,8
|
146,0
|
124,8
|
103,6
|
119,0
|
108,7
|
2. Оценка параметров модели 1МНК в матричной форме
Предположим, что все предпосылки классической регрессионной модели выполняются и осуществим оценку параметров модели по формуле:
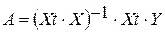
Алгоритм вычисления параметров модели
1. Вычисляем матрицу моментов Xt*X, но сначала найдем транспонированную матрицу Хt.
| 1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
1,0
|
| Xtrans=
|
38,8
|
39,9
|
30,1
|
31,7
|
17,2
|
39,7
|
36,9
|
38,2
|
40,1
|
| 114,0
|
101,1
|
153,8
|
146,0
|
124,8
|
103,6
|
119,0
|
108,7
|
106,5
|
Xt*X
| 9
|
312,6
|
1077,5
|
| 312,6
|
11309,14
|
36788,2
|
| 1077,5
|
36788,24
|
131815
|
2. Вычисляем матрицу ошибок 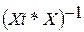
| 17,645098
|
-0,201192
|
-0,0881
|
| -0,2011917
|
0,003254
|
0,00074
|
| -0,0880866
|
0,000737
|
0,00052
|
3. Находим матрицу-произведение Xt*Y
4. Вычисляем вектор оценок параметров модели как произведение матрицы 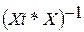 на матрицу Xt*Y на матрицу Xt*Y
| По формуле
|
Регрессия коэффициенты
|
| 1,2597249
|
а0
|
У – пересечение
|
1,25972
|
| -0,0106048
|
а1
|
Х1
|
-0,0106
|
| 0,012072
|
а2
|
Х2
|
0,01207
|
Таким образом, оценка эконометрической модели имеет вид
y=1,2597249–0,0106048+0,012072x2
3. Коэффициенты множественной детерминации и корреляции для оцененной модели
3.1 Расчет коэффициентов множественной детерминации и корреляции
Для оценки степени соответствия полученной модели наблюдаемым данным, то есть предварительной оценки адекватности модели, вычисляем коэффициенты множественной детерминации и множественной корреляции.
Коэффициент множественной корреляции является степень соответствия оцененной модели фактическим данным и рассчитывается как коэффициент корреляции между y
и 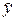 . .
Квадрат коэффициента множественной корреляции называется коэффициентом множественной детерминации. Коэффициент множественной детерминации характеризует часть дисперсии показателя у
, что объясняется регрессией, т.е. вариацией факторов, которые входят в модель:
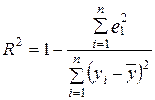
Коэффициент множественной корреляции удобно рассчитывать как корень из коэффициента множественной детерминации, т.е.
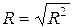
Алгоритм вычисления коэффициентов множественной детерминации и корреляции:
1. Скопируем с итогового листа инструмента анализа Регрессия
– Регрессия значения столбцов Предсказанное У
и Остатки
в таблицу 4.
2. Вычислим среднее значение у расчетного
3. В третий столбец введем формулу общих отклонений у-уср. и просчитаем ее для всех наблюдений.
4. Вычислим суммы квадратов общих отклонений и отклонений, которые не объясняются регрессией (остатков).
5. Вычислим коэффициент множественной детерминации 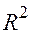 . .
6. Рассчитаем коэффициент множественной корреляции R.
7. Для проверки полученных коэффициентов скопируем с итогового листа Регрессия значения ячеек R-квадрат и Множественный R. Значения совпали.
Таблица 4 – Расчет коэффициентов 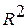 и и 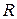
| Факт.
|
Предсказанное Y
|
Остатки
|
Y
|
Y-Y
|
| 2,48
|
2,22446
|
0,0955378
|
2,224462
|
-0,0167
|
| 2,62
|
2,05707
|
0,1329312
|
2,057069
|
-0,1467
|
| 2,88
|
2,79719
|
0,0328127
|
2,797187
|
0,4933
|
По формуле
|
Регрессия
|
| 2,68
|
2,68606
|
0,0639415
|
2,686058
|
0,4133
|
R-квадрат
|
| 2,52
|
2,5839
|
0,0060977
|
2,583902
|
0,2533
|
0,78
|
0,78
|
| 2,74
|
2,08937
|
0,1806303
|
2,08937
|
-0,0667
|
Коеф. мн. корреляций
|
| 2,56
|
2,30497
|
-0,254971
|
2,304971
|
-0,2867
|
0,88
|
0,88
|
| 2,68
|
2,16684
|
-0,2168438
|
2,166844
|
-0,3867
|
| 2,55
|
2,12014
|
-0,0401364
|
2,120136
|
-0,2567
|
| 2,3367
|
2,3367
|
| 0,17827
|
0,8022
|
3.2 Разложение коэффициента множественной детерминации на коэффициенты отдельной детерминации
Для определения доли влияния каждого фактора на показатель используют коэффициенты отдельной детерминации.
Коэффициентом отдельной детерминации
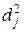 для фактора для фактора 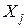 называется произведение коэффициента корреляции называется произведение коэффициента корреляции 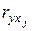 между фактором между фактором 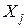 и показателем У на стандартизованный параметр регрессии и показателем У на стандартизованный параметр регрессии 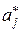 : :
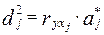 , ,
Сумма коэффициентов отдельной детерминации равняется коэффициенту множественной детерминации:
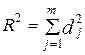
Во время анализа двухфакторной модели коэффициенты отдельной детерминации рассчитываются по формулам:
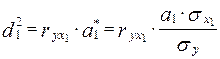

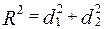
Теперь рассчитаем коэффициенты отдельной детерминации по этим формулам. Полученное значение 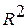 совпало с тем, которое рассчитали ранее. совпало с тем, которое рассчитали ранее.
Таблица 5 – Расчет коэффициентов отдельной детерминации
| d12
|
0,1649
|
| d22
|
0,6128
|
| R2
|
0,7778
|
3.3 Предварительные выводы об адекватности модели
С помощью полученных коэффициентов множественной детерминации, корреляции и отдельной детерминации можно сделать предварительные выводы об адекватности модели.
1) Поскольку коэффициент множественной детерминации R2
= 0,7778, то это свидетельствует про то, что вариация общих затрат на предприятиях на 77,78% определяется вариацией затрат оборота и трудоемкостью и на 22,22% вариацией показателей, которые не учитываются в модели.
2) Поскольку коэффициенты отдельной детерминации d1=0,1649, то это свидетельствует о том, что вариация общих затрат на предприятиях на 16,49% определяется вариацией затрат оборота
3) Коэффициент множественной корреляции R2
= 0,7778 характеризует сильную связь между общими затратами и факторами, которые их обуславливают.
4. Оценка дисперсионно – ковариационной матрицы оценок параметров модели
4.1 Оценка дисперсии отклонений
Вычислим оценку дисперсии отклонений по формуле
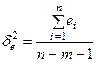 , ,
где  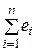 – сумма квадратов отклонений; – сумма квадратов отклонений;
n
– количество наблюдений;
m
– количество факторов модели.
Полученное значение проверим копированием с итогового листа Регрессии
значение ячейки Остаток
с таблицы дисперсийного анализа. Значения совпали.
Таблица 6 – Оценка дисперсии остатков
| По формуле
|
Регрессия
|
| MS
|
| 0,0297117
|
Остаток
|
0,0297117
|
4.2 Расчет дисперсии и ковариации оценок параметров модели
Для получения оценок ковариаций и дисперсий оценок параметров модели необходимо сложить ковариационную матрицу по формуле:
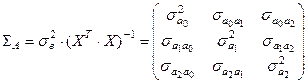
Таблица 7 – Оценка ковариационной матрицы оценок параметров модели
| 17,6451
|
-0,201192
|
-0,08809
|
0,5243
|
-0,006
|
-0,003
|
| 0,0297117
|
-0,20119
|
0,0032538
|
0,000737
|
-0,006
|
1E-04
|
2E-05
|
| -0,08809
|
0,0007365
|
0,000522
|
-0,0026
|
2E-05
|
2E-05
|
Мы получили дисперсии оценок параметров модели, которые расположены по главной диагонали:
| σ =
|
0,5243
|
σ =
|
1E-04
|
σ =
|
2E-05
|
4.3 Вычисление стандартных ошибок параметров и выводы о смещенности оценок параметров модели
Стандартные ошибки параметров модели рассчитаем по формуле 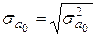 , , 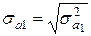 , , 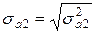 . Для получения стандартной ошибки оценки параметров а0 введем формулу возведения в степень 0,5. И аналогично получим стандартные ошибки оценок параметров а1 и а2. Для проверки полученных ошибок скопируем с итогового листа Регрессия
значения ячеек столбца Стандартная ошибка
. Значения совпали. . Для получения стандартной ошибки оценки параметров а0 введем формулу возведения в степень 0,5. И аналогично получим стандартные ошибки оценок параметров а1 и а2. Для проверки полученных ошибок скопируем с итогового листа Регрессия
значения ячеек столбца Стандартная ошибка
. Значения совпали.
Сравним каждую стандартную ошибку с соответствующим значением оценки параметра с помощью формулы:
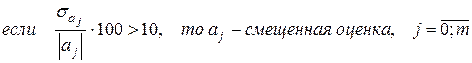
Таблица 8 – Расчет стандартных ошибок оценок параметров модели. Выводы о смещении оценок параметров модели
| Регрессия
|
| По формуле
|
Стандартная ошибка
|
Выводы о смещённости оценок параметров модели
|
| 0,72406211
|
0,7240621
|
57,47779
|
Оценка смещена
|
| 0,00983242
|
0,0098324
|
-92,717
|
Оценка не смещена
|
| 0,00393854
|
0,0039385
|
32,62555
|
Оценка смещена
|
5. Проверка гипотез о статистической значимости оценок параметров модели на основе F- и t-критериев
5.1 Проверка адекватности модели по критерию Фишера
Проверку адекватности модели по критерию Фишера проведем по представленному алгоритму.
Шаг 1
.
Формулирование нулевой и альтернативной гипотез.
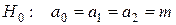 , т.е. не один фактор модели не влияет на показатель. , т.е. не один фактор модели не влияет на показатель.
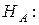 Хотя бы одно значение Хотя бы одно значение 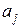 отменно от нуля, т.е. отменно от нуля, т.е. 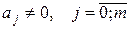
Шаг 2.
Выбор соответствующего уровня значимости.
Уровнем значимости 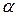 называется вероятность сделать ошибку 1-го рода, т.е. отвергнуть правильную гипотезу. Величина называется вероятность сделать ошибку 1-го рода, т.е. отвергнуть правильную гипотезу. Величина 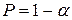 называется уровнем доверия или доверительной вероятностью. называется уровнем доверия или доверительной вероятностью.
Выбираем уровень значимости 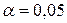 , т.е. доверительная вероятность – Р=0,95 , т.е. доверительная вероятность – Р=0,95
Шаг 3.
Вычисление расчетного значения F-критерия.
Расчетное значение F-критерия определяется по формуле:
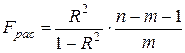
Для проверки полученного значения скопируем с итогового листа Регрессия расчетное значение F-критерия. Значения совпали 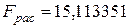
Шаг 4.
Определение по статистическим таблицам F-распределения Фишера критического значения F-критерия.
Критическое значение F-критерия находим по статистическим таблицам F-распределения Фишера по соответствующим данным:
- доверительной вероятности Р=0,95;
- степеней свободы 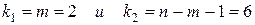
Определяем табличное значение критерия 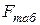 =5,14 =5,14
Шаг 5.
Сравнение рассчетного значения F-критерия с критическим и интерпритация результатов.
Вывод о принятии нулевой гипотезы, т.е. об адекватности модели делаем с помощью встроенной логической функции ЕСЛИ.
Поскольку 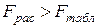 , то отвергаем нулевую гипотезу про незначимость факторов с риском ошибиться не больше чем на 5% случаев, т.е. с надежностью Р=0,95 можно считать, что принятая модель адекватна статистическим данным и на основе этой модели можно осуществлять экономический анализ и прогнозирование. , то отвергаем нулевую гипотезу про незначимость факторов с риском ошибиться не больше чем на 5% случаев, т.е. с надежностью Р=0,95 можно считать, что принятая модель адекватна статистическим данным и на основе этой модели можно осуществлять экономический анализ и прогнозирование.
5.2 Проверка значимости оценок параметров модели по критерию Стьюдента
Проверку гипотезы о значении каждого параметра модели проведем в соответствии с представленным алгоритмом.
Шаг 1
.
Формулирование нулевой и альтернативной гипотез.
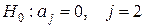 – оценка j-го параметра является статистически незначимой, т.е. j-й фактор никак не влияет на показатель у
; – оценка j-го параметра является статистически незначимой, т.е. j-й фактор никак не влияет на показатель у
;
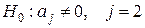 – оценка j-го параметра является статистически значимой, т.е. j-й фактор влияет на показатель у
. – оценка j-го параметра является статистически значимой, т.е. j-й фактор влияет на показатель у
.
Шаг 2.
Выбор соответствующего уровня значимости.
Выбираем уровень значимости 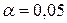 , т.е. доверительная вероятность – Р=0,95. , т.е. доверительная вероятность – Р=0,95.
Шаг 3.
Вычисление расчетного значения t-критерия.
Расчетное значение t-критерия определяется по формуле:
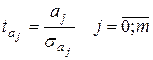
Во время анализа двухфакторной модели расчетные значения t-критерия определяются по формулам:
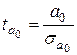 =-3,2333 =-3,2333 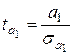 =3,4264 =3,4264 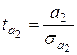 =4,9937 =4,9937
Для проверки полученного значения t-критерия скопируем с итогового листа Регрессия значения ячеек столбца t
-статистика
. Значения совпали.
Шаг 4.
Определение по статистическим таблицам t-распределения Стьюдента критического значения t-критерия.
Критическое значение t-критерия находим по статистическим таблицам t-распределения Стьюдента по соответствующим данным:
- доверительной вероятности Р=0,95;
- степеней свободы 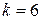
Определяем табличное значение критерия 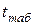 =2,45 =2,45
Шаг 5.
Сравнение рассчетного значения t-критерия с критическим и интерпритация результатов.
Выводы о принятии нулевой гипотезы, т.е. о значимости оценок параметров 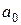 , , 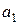 и и 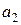 делаем с помощью встроенной логической функции ЕСЛИ. С надежностью Р=0,95 можно считать, что делаем с помощью встроенной логической функции ЕСЛИ. С надежностью Р=0,95 можно считать, что
– оценки 1-го и 2-го параметров модели значимые, т.е. оба фактора существенно влияют на показатель;
– оценка 0-го параметра модели не является статистически значимой.
Таблица 9 – Проверка гипотез о статистической значимости оценок параметров модели на основе F- и t – критериев
| F-критерий Фишера
|
| По формуле
|
Регресия
|
Р=0.95
|
| F
|
2,45
|
| 10,4997302
|
10,499730
|
Модель адекватна
|
| t-критерий Стьюдента
|
|
| По формуле
|
Регресия
|
Р=0.95
|
| t-статистика
|
5,14
|
| 1,73980232
|
1,739802
|
а0
|
Параметр не значимый
|
| -1,0785514
|
-1,07855
|
а1
|
Параметр не значимый
|
| 3,06508252
|
3,06508
|
а2
|
Параметр не значимый
|
6. Построение интервалов доверия для параметров модели.
Интервалом доверия
называется интервал, который содержит неизвестный параметр с заданным уровнем доверия.
Интервалы доверия для параметров находим аналогично процедуре тестирования нулевой гипотезы по t-критерию Стьюдента:
– выбираем уровнем значимости 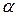 =0,05 и соответственно уровень доверия будет составлять – Р=0,95; =0,05 и соответственно уровень доверия будет составлять – Р=0,95;
– для каждого параметра вычисляем нижнюю и верхнюю границы интервала доверия по формуле, при этом делаем абсолютную ссылку на табличное значение t-критерия 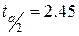 : :
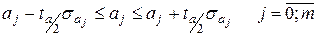
где 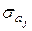 - стандартная ошибка параметров модели - стандартная ошибка параметров модели 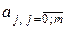
Для проверки полученных значений границ скопируем с итогового листа Регрессия значения ячеек столбцов Нижнее 95%
и Верхнее 95%
. Значения совпали.
Таблица 10 – Доверительные интервалы для оценок параметров
| По формуле
|
Регресия
|
| Нижние 95%
|
Верхние 95%
|
Нижние 95%
|
Верхние 95%
|
| -0,5119912
|
3,031441
|
-0,511991215
|
3,031441101
|
| -0,3466383
|
0,013454
|
-0,034663831
|
0,013454293
|
| 0,00243469
|
0,021709
|
0,00243469
|
0,02170921
|
Исходя из этого, 95% интервалы доверия для параметров модели имеют вид:
-0,5119912≤а0≤3,031441
-0,3466383≤а1≤0,013454
0,00243469≤а2≤0,021709
7. Расчет прогнозного значения рентабельности на основании оцененной модели
Так как оцененная модель является адекватной статистическим данным, то на основании этой модели можно осуществлять прогнозирование рентабельности для одного из предприятий объединения, деятельность которого исследовалась.
7.1 Точечный прогноз рентабельности
Сделаем точечный прогноз рентабельности для одного из предприятий при условии того, что затраты оборота составят 7 г.о. и трудоемкость – 50 г.о., т.е. 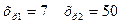 , по формуле: , по формуле:
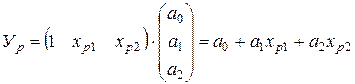
| Хр
|
| 1
|
16
|
100
|
1,25972494
|
| -0,01060477
|
2,297243652
|
| 0,01207195
|
7.2 Доверительный интервал для прогноза математического ожидания рентабельности
Рассчитаем значения верхней и нижней границ прогнозного интервала, используя табл. значения критерия Стьюдента 2,45, по формуле:
Оценку дисперсий матожидания вычислим по формуле:

Интервальный прогноз матожидания рентабельности:
Стандартная ошибка матожидания
| 0,524265941
|
-0,005977749
|
-0,0026172
|
1
|
| 1
|
16
|
100
|
-0,005977749
|
9,66765E-05
|
2,18828E-05
|
16
|
| -0,002617204
|
2,18828E-05
|
1,55121E-05
|
100
|
| 1
|
| 0,16690155
|
-0,002
|
-0,000716
|
16
|
0,059432144
|
| 100
|
оценка дисперсионного прогноза
| нижняя граница
|
1,7
|
| верхняя граница
|
2,895
|
Таким образом, 95% интервал доверия для прогноза матожидания рентабельности имеет вид 1,7 2,895. 2,895.
7.3 Доверительный интервал для прогноза рентабельности
Для нахождения интервального прогноза индивидуального значения рентабельности вычислим стандартную ошибку прогноза индивидуального значения по формуле:
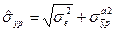
А значение нижней и верхней границ по формуле:
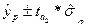
| Стандартная ошибка прогноза индивидуального значения
|
0,298569664
|
| нижняя граница
|
1,565747976
|
| верхняя граница
|
3,028739328
|
Таким образом можно утверждать, что прогнозное значение затрат принадлежит интервалу 1,565747976≤Ур≤3,028739328.
8. Экономический анализ по уцененной модели.
Т. к. оцененная модель является адекватной статистическим данным, то на основе этой модели можно осуществлять экономический анализ процесса, который исследуется, для этого рассчитаем граничные и средние показатели.
Средней эффективностью (продуктивность) фактора называется объем результирующего показателя, который приводится на ед. затрат фактора в среднем.
Средняя эффективность i-го фактора определяется по формуле:
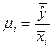 Предельной эффективностью(продуктивностью) называется изменение объема результирующего показателя за счет изменения этого фактора на единицу при неизменных других факторах, которые влияют на объем результирующего показателя. Предельной эффективностью(продуктивностью) называется изменение объема результирующего показателя за счет изменения этого фактора на единицу при неизменных других факторах, которые влияют на объем результирующего показателя.
Предельной эффективность i-го показателя определяется по формуле:
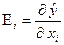 ; ; 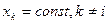
Частичный коэффициент эластичности показывает на сколько процентов изменится результирующий показатель, если i-ый фактор изменится на один процент при неизменных значениях других факторов.
Частичный коэффициент эластичности i-го показателя определяется по формуле:
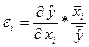 ; ; 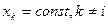
Суммарным коэффициентом эластичности называется сумма частичных коэффициентов эластичности.
Граничная норма замещения j-го фактора i-тым показывает количество единиц i-го фактора необходимую для замены j-го фактора при постоянном объеме результирующего показателя и других факторов и рассчитывается по формуле:
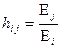 ; ; 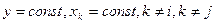
Таблица 11-Расчет средних и граничных показателей
| Средняя эффективность фактора
|
Граничная эффективность фактора
|
Частичная эластичность рентабельности
|
Суммарная эластичность
|
Граничная норма замещения факторов
|
| Затраты оборота, х1
|
0,067274472
|
0,019517401
|
3,446896993
|
5,063653297
|
0,290116009
|
| Трудоемкость, х2
|
0,019517401
|
0,01207195
|
1,616756304
|
3,446896993
|
Анализ полученных результатов приводит к таким выводам:
1) На основе значения средней эффективности затрат оборота можно утверждать, что на 1 д.е.затрат оборота приходится 0,067 общих затрат.
2) На основе значения средней эффективности трудоемкости можно утверждать, что на 1 д.е.трудоемкости приходится 0,0195 общих затрат.
3) На основе значения граничной эффективности затрат оборота можно утверждать, что при увеличении затрат оборота на 1 г.о. объем общих затрат увеличится на 0,0195 д.е. при неизменном объеме трудоемкости.
4) На основе значения граничной эффективности трудоемкости можно утверждать, что при увеличении затрат оборота на 1 г.о. объем общих затрат увеличится на 0,012 д.е. при неизменном объеме затрат оборота.
5) На основе значения коэффициента частичной эластичности по фактору Х1 можно утверждать, что при увеличении затрат оборота на 1% общих затрат увеличится на 3,44% при неизменном объеме трудоемкости.
6) На основе значения коэффициента частичной эластичности по фактору Х2 можно утверждать, что при увеличении трудоемкости на 1% объем общих затрат увеличится на 1,62% при неизменном объеме затрат оборота.
7) На основе граничной нормы замены 2-го фактора первым можно утверждать, что для замены 1 д.е. трудоемкости нужно будет 0,29 д.е.затрат оборота при сохранении неизменного объема общих затрат.
8) На основе граничной нормы замены 1-го фактора вторым можно утверждать, что для замены 1 д.е.затрат оборота нужно будет 3,5 д.е.трудоемкости при сохранении неизменного объема общих затрат.
Исследование наличия мультиколлениарности по алгоритму Феррара-Глобера
Условие задачи
Допустим, что на уровень рентабельности предприятий общественного питания существенно влияют такие показатели общественной деятельности:
Относительный уровень затрат оборота (%), часть продукции собственного производства (%) и численность работников в расчете на 1 тыс. товарооборота (чел.)
Чтобы построить эконометрическую модель этой зависимости по методу 1МНК необходимо быть уверенным, что между факторами относительного уровня затрат оборота, частью собственной продукции и трудоемкостью не существует мультиколлинеарности.
Мультиколлинеарность
обозначает существование тесной линейной зависимости или сильной корреляции между двумя или более факторами.
Исследовать наличие мультиколлинеарности между этими факторами по данным десяти предприятий общественного питания города, которые приведены в таблице.
Вариант 3.
| № п\п
|
Уровень затрат
|
Собственная продукция
|
Трудоемкость
|
| 1
|
16,9
|
40,4
|
20,2
|
| 2
|
16,2
|
18,9
|
21,3
|
| 3
|
15,5
|
16,6
|
31,4
|
| 4
|
18,2
|
41,4
|
18,9
|
| 5
|
17,3
|
12,2
|
24,8
|
| 6
|
17,1
|
31,4
|
19,4
|
| 7
|
16,4
|
32,6
|
19,3
|
| 8
|
16,7
|
38,7
|
19,6
|
| 9
|
14,2
|
44,3
|
25,7
|
| 10
|
17,2
|
39,3
|
22,1
|
Исследование наличия мультиколлинеарности по алгоритму Феррара-Глобера
1.
Идентификация переменных.
У – уровень рентабельности предприятий – результирующий показатель.
Х1 – относительный уровень затрат оборота – показатель-фактор.
Х2 – часть продукции собственного производства – показатель-фактор.
Х3 – трудоемкость – показатель-фактор.
Таблица 1- Исходные данные, построение матрицы стандартизированных переменных
| №п\п
|
Х1
|
Х2
|
Х3
|
Хi1-X1
|
Хi2-X2
|
Хi3-X3
|
Хi1*
|
Хi2*
|
Хi3*
|
| 1
|
15,6
|
19,2
|
21,1
|
-0,05
|
-24,79
|
-0,42
|
-0,015500616
|
-0,876
|
-0,0602
|
| 2
|
13,5
|
41
|
27,8
|
-2,15
|
-2,99
|
6,28
|
-0,666526495
|
-0,106
|
0,8998
|
| 3
|
15,3
|
41,3
|
21,7
|
-0,35
|
-2,69
|
0,18
|
-0,108504313
|
-0,095
|
0,0258
|
| 4
|
14,9
|
45,2
|
21,5
|
-0,75
|
1,21
|
-0,02
|
-0,232509242
|
0,0428
|
-0,0029
|
| 5
|
15,1
|
50,2
|
21,1
|
-0,55
|
6,21
|
-0,42
|
-0,170506778
|
0,2195
|
-0,0602
|
| 6
|
16,1
|
51,6
|
19,7
|
0,45
|
7,61
|
-1,82
|
0,139505545
|
0,2689
|
-0,2608
|
| 7
|
16,7
|
48
|
19,6
|
1,05
|
4,01
|
-1,92
|
0,325512939
|
0,1417
|
-0,2751
|
| 8
|
15,4
|
48,6
|
21,2
|
-0,25
|
4,61
|
-0,32
|
-0,077503081
|
0,1629
|
-0,0458
|
| 9
|
17,1
|
49,8
|
20,2
|
1,45
|
5,81
|
-1,32
|
0,449517869
|
0,2053
|
-0,1891
|
| 10
|
16,8
|
45
|
21,3
|
1,15
|
1,01
|
-0,22
|
0,356514172
|
0,0357
|
-0,0315
|
| Сумм
|
156,5
|
439,9
|
215,2
|
Матрица
|
| Средн
|
15,65
|
43,99
|
21,52
|
стандартизованных
|
| Суммкв
|
10,405
|
800,8
|
48,716
|
переменных Х*
|
2. Исследование наличия мультиколлинеарности по алгоритму Феррара-Глобера.
Шаг 1. Стандартизация переменных.
Элементы стандартизованных векторов рассчитываются по формулам:
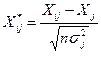 , i=1; n, j=1; m. , i=1; n, j=1; m.
где n – число наблюдений;
m – число факторов;
σj
2
– дисперсия j-го фактора.
Поскольку дисперсия рассчитывается по формуле:
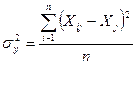 , ,
то формуле для стандартизации переменных примут вид:
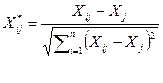 , i=1; n, j=1; m. , i=1; n, j=1; m.
Шаг 2. Нахождение корреляционной матрицы
R
(матрицы моментов стандартизованной системы нормальных уравнений).
Корелляционная матрица R определяется по формуле:
R=Х*Т
·Х*,
где Х* – матрица стандартизованных переменных.
Для нахождения элементов корелляционной матрицы R последовательно используем встроенные функции Транспонирование матриц – ТРАНСП и Произведение матриц – МУМНОЖ.
Проверку вычислений следует выполнять, и используя последовательно встроенную функцию КОРРЕЛ, учитывая при этом свойства корреляционной матрицы: корреляционная матрица является симметричной, на главной диагонали расположены единицы.
Таблица 2 – Нахождение корреляционной матрицы
| Транспонированная матрица стандартизированных переменных
|
| -0,01550062
|
-0,6665
|
-0,1085
|
-0,2325092
|
-0,171
|
0,14
|
0,32551
|
-0,0775
|
0,4495
|
0,3565
|
| -0,87603791
|
-0,1057
|
-0,09506
|
0,0427594
|
0,2195
|
0,269
|
0,14171
|
0,16291
|
0,2053
|
0,0357
|
| -0,06017464
|
0,89975
|
0,025789
|
-0,0028655
|
-0,06
|
-0,261
|
-0,2751
|
-0,0458
|
-0,189
|
-0,0315
|
| Корреляционная матрица
|
| 1
|
0,222996
|
-0,8092664
|
Проверка
|
1
|
0,223
|
-0,809
|
| R
|
0,223
|
1
|
-0,2146624
|
R
|
0,223
|
1
|
-0,215
|
| -0,8093
|
-0,21466
|
1
|
-0,8093
|
-0,2147
|
1
|
Коэффициент корреляции между факторами Х1 и Х2=0,223
Коэффициент корреляции между факторами Х1 и Х3=-0,8093
Коэффициент корреляции между факторами Х2 и Х3=-0,21466.
Вывод: на основании значения коэффициента корреляции rX
2
X
3
=-0,21466. можно сделать предварительный вывод о наличии возможной мультиколлинеарности между факторами Х2 и Х3.
Шаг 3. Критерий – Х2
.
Расчетное значение критерия Х2
определяется по формуле:
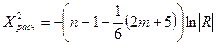 , ,
где 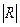 -определитель корреляционной матрицы R-детерминант корреляции. -определитель корреляционной матрицы R-детерминант корреляции.
По заданной доверительной вероятности Р и числу степеней свободы
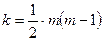 находится табличное значение критерия Х2
табл
, которое сравнивается с расчетным. находится табличное значение критерия Х2
табл
, которое сравнивается с расчетным.
– если Х2
расч
< Х2
табл
, то нет оснований отклонить гипотезу об отсутствии мультиколлинеарности в массиве факторов, то есть с принятой надежностью можно утверждать, что в массиве факторов мультиколлинеарность отсутствует;
– если Х2
расч
> Х2
табл
, то гипотеза об отсутствии мультиколлинеарности в массиве факторов отклоняется, то есть с принятой надежностью можно утверждать, что в массиве факторов мультиколлинеарность существует.
Примечание:
Если гипотеза об отсутствии мультиколлинеарности в массиве факторов принимается, то исследования мультиколлинеарности останавливаются.
Выберем уровень значимости ά=0,05, следовательно доверительная вероятность Р=0,95. Число степеней свободы k=3. Табличное значение критерия Х2
табл
=Х2
(0,95; 3)=7,8.
Исследование наличия мультиколлинеарности в массиве факторов по критерию Х2
в оболочке электронных таблиц
Excel
.
1. Находим определитель матрицы, используя встроенную функцию МОПРЕД.
2. Находим натуральный логарифм определителя, используя встроенную математическую функцию LN.
3. Находим расчетное значение критерия.
4. Вводим расчетное значение.
5. Делаем вывод о наличии мультиколлинеарности в массиве факторов, используя встроенную логическую функцию ЕСЛИ.
Таблица 3=Критерий Х2
.
| Таблица 3
|
| Определитель корреляционной матрицы
|
0,326758051
|
| Натуральный логарифм определителя
|
-1,118535287
|
| Расчетное значение критерия
|
8,016169558
|
| Табличное значение критерия
|
7,8
|
| Вывод о наличии в массиве факторов мультиколлиниарности
|
В массиве факторов существует мультиколлинеарность
|
Выводы:
– на основании значения детерминанта корреляции 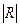 =0,33 (→0) можно сделать предварительный вывод о наличии мультиколлинеарности в массиве факторов; =0,33 (→0) можно сделать предварительный вывод о наличии мультиколлинеарности в массиве факторов;
– на основании критерия – Х2
с надежностью Р=0.95 можно утверждать, что в массиве факторов есть мультиколлинеарность.
Шаг 4.
F
-критерий Фишера.
Расчетные значения F-критерия для каждого фактора определяются по формуле:
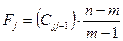 , j=1,2…m , j=1,2…m
где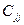 - диагональные элементы матрицы С=R-1
; - диагональные элементы матрицы С=R-1
;
По заданной доверительной вероятности Р и числом степеней свободы:
– k1
=m-1 – степень свободы знаменателя;
– k2
=n-m – степень свободы числителя(k1
< k2
).
Находится табличное значение F-критерия, которое сравнивается з расчетным:
– если Fj
расч
< Fj
табл
, то нет оснований отклонить гипотезу об отсутствии мультиколлинеарности между J-тым фактором и остальным массивом, то есть с принятой надежностью можно утверждать, что между J-тым фактором и другими мультиколлинеарность отсутствует;
– если Fj
расч
> Fj
табл
, то гипотеза об отсутствии мультиколлинеарности между J-тым фактором и остальным массивом отклоняется, то есть с принятой надежностью можно утверждать, что между J-тым фактором и другими мультиколлинеарность существует.
Выбираем уровень значимости ά=0,05, следовательно, доверительная вероятность Р=0,95. Число степеней свободы k1=2, k2=7. Табличное значение критерия F0,95
(2; 7)=4,74.
Исследования наличия мультиколлинеарности каждого фактора со всеми другими факторами массива по
F
-критерию Фишера в оболочке электронных таблиц
Excel
.
1. Находим расчетные значения критерия F1
, F2
, F3
соответственно.
2. Вводим табличное значение критерия.
3. Делаем вывод об отсутствии мультиколлинеарности фактора Х1 и факторами Х2 и Х3, используя встроенную логическую функцию ЕСЛИ.
Поскольку функция будет копироваться в остальные ячейки столбца, то при введении адрес ячеек, которые сравниваются, нужно использовать абсолютную и относительную ссылку.
4. Копируем полученную формулу в две нижние ячейки и делаем выводы о наличии мультиколлинеарности фактора Х2 с факторами Х1 и Х3 и Х3 с факторами Х1 и Х2.
Таблица 4-F-критерий Фишера
| Матрица,
|
2,91934678
|
-0,1508
|
2,3302
|
| обратная корреляционной С
|
-0,15080461
|
1,056096
|
0,1047
|
| матрице
|
2,330157238
|
0,104663
|
2,9082
|
| Значение F1 и вывод
|
6,71771373
|
Между факторм и другими мультиколлиниарность существует
|
| Значение F2 и вывод
|
0,196335919
|
Между фактором и другими мультиколлинеарность отсутствует
|
| Значение F3 и вывод
|
6,678648215
|
Между факторм и другими мультиколлиниарность существует
|
| Табличное значение
|
4,74
|
| F – критерия
|
Выводы:
– между фактором Х1 и факторами Х2 и Х3 существует мультиколлинеарность;
– между фактором Х2 и факторами Х1 и Х3 не существует мультиколлинеарности;
– между фактором Х3 и факторами Х2 и Х1 существует мультиколлинеарность;
Шаг 6. Расчет коэффициентов частичной корреляции.
Коэффициенты частичной корреляции рассчитываются по формулам:
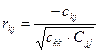 , k=1; m, j=1; m , k=1; m, j=1; m
где Cjj
, Ckk
– диагональные элементы матрицы С=R-1
Ckj
– элемент матрицы С=R-1
, который находится в k-той строке и в j-том столбце.
Поскольку для массива факторов, которые исследуются m=3, то необходимо рассчитывать 3 коэффициента частичной корреляции r12(3)
, r13(2)
, r23(1)
.
Шаг 7.
t
– критерий Стьюдента.
Расчетные значения t – критерия для каждой пары факторов определяются по формулам:
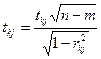 , k=1; m, j=1; m, , k=1; m, j=1; m,
где rkj
– соответствующие коэффициенты частичной корреляции.
По заданной доверительной вероятности З и числом степеней свободы k=n-m находится табличное значение, которое сравнивается с расчетным:
– если tjj
расч
<tjj
табл
, то нет оснований отклонить гипотезу об отсутствии мультиколлиниарности между k-тым и j-тым факторами, то есть с принятой надежностью можно утверждать, что между k-тым и j-тым факторами мультиколлинеарность отсутствует.
– если tjj
расч
>tjj
табл
, то гипотеза об отсутствии мультиколлинеарности между k-тым и j-тым факторами отклоняется, то есть с принятой надежностью можно утверждать, что между k-тым и j-тым факторами мультиколлинеарность существует.
Выберем уровень значимости ά=0,05, таким образом, доверительная вероятность Р= 0,95. Число степеней свободы k=7. Табличное значение критерия t0,95
(7)=1,89.
Исследование наличия мультиколлинеарности для каждой пары факторов по критерию Стьюдента в оболочке электронных таблиц
Excel
.
1. Расчетные значения находим по формуле.
2. Вводим табличное значение критерия.
3. Модуль расчетного значения критерия r12(3
находим, используя встроенную математическую функцию ABS, при этом делаем относительную ссылку на столбец.
4. Делаем вывод о наличии мультиколлиниарности между факторами Х1 и Х2, используя встроенную логическую функцию ЕСЛИ. При этом делаем относительную и абсолютную ссылку.
5. Полученную формулу копируем и делаем выводы о наличии мультиколлиниарности между факторами Х1 и Х3, Х2 и Х3.
Таблица 5 – t – критерий Стьюдента
| Коэффициэнты частичной корреляции
|
| r12 (3)
|
0,085885547
|
| r13 (2)
|
-0,79970784
|
| r23(1)
|
-0,10466296
|
| Значение t-критерия
|
Модули
|
Выводы о наличии мультиколлиниарности
|
| t12 (3)
|
0,228074533
|
0,228075
|
Между факторами отсутствует мультиколлинеарность
|
| t13 (2)
|
-3,52409329
|
3,524093
|
Между факторома существует мультиколлинеарность
|
| t23(1)
|
-0,27844144
|
0,278441
|
Между факторами отсутствует мультиколлинеарность
|
| tтабл
|
1,89
|
Выводы: с надежностью Р=0,95 можно утверждать, что:
– между факторами Х1 и Х2 мультиколлинеарность отсутствует;
– между факторами Х1 и Х3 мультиколлинеарность существует;
– между факторами Х2 и Х3 мультиколлинеарность отсутствует;
Общий вывод: Таким образом между факторами 1 и 3 модели, т.е. между относительным уровнем затрат оборота и трудоемкостью существует мультиколлинеарность. Построить модель методом 1МНК нельзя, так как между факторами существует мультиколлинеарность.
|