Лабораторная работа: Анализ накладных расходов
|
Название: Анализ накладных расходов Раздел: Рефераты по математике Тип: лабораторная работа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Всероссийский заочный финансово-экономический институт Кафедра экономико-математических методов и моделей
Лабораторная работа по эконометрике Вариант 8 Липецк 2007 Анализ накладных расходов По данным, представленным в табл. 1, исследуется зависимость между величиной накладных расходов 40 строительных организаций Y (млн. руб.) и следующими тремя основными факторами: x1 – объемом выполненных работ, млн. руб. x2 – численностью рабочих, чел. x3 – фондом зарплаты, млн. руб. Таблица 1
Задание 1
1. Построить уравнение множественной регрессии в линейной форме с полным набором факторов, отобрать информативные факторы в модель по t-критерию для коэффициентов регрессии. 2. Построить уравнение множественной регрессии только со значимыми факторами, рассчитать индекс корреляции R и оценить качество полученного уравнения регрессии с помощью коэффициента детерминации. 3. Оценить статистическую значимость уравнения регрессии, используя критерий Фишера F(α=0,05) и статистическую значимость параметров регрессии, используя критерий Стьюдента. 4. Дать сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности, β- и ∆-коэффициентов. 5. Проверить выполнение предпосылок МНК, в том числе провести тестирование ошибок уравнения регрессии на гетероскедастичность. Задание 1 С помощью инструмента Регрессия (Анализ данных в Excel) построим уравнение множественной регрессии в линейной форме с полным набором факторов:
Результат регрессионного анализа содержится в таблицах 2 – 4: Таблица 2
Таблица 3. Дисперсионный анализ
Таблица 4
Уравнение регрессии выглядит следующим образом: y= 1,132+ 0,060x1 + 0,001x2 +0,103x3 . Для отбора информативных факторов в модель воспользуемся инструментом Корреляция (Excel). Получим
Анализ матрицы коэффициентов парной корреляции показывает, что накладные расходы имеют тесную связь с фондом заработной платы (ryx 3 =0,815), с объемом работ и с численностью рабочих. Однако факторы X1 и X3 тесно связаны между собой (ryx 1 x3 =0,825), что свидетельствует о наличии мультиколлинеарности. Из этих двух переменных оставим в модели X1 – объем работ. Задание 2 С помощью инструмента Регрессия (Анализ данных в Excel) построим уравнение множественной регрессии только со значимыми факторами. Результат регрессионного анализа содержится в таблицах 5 – 8: Таблица 5. Регрессионная статистика
Таблица 6. Дисперсионный анализ
Таблица 7
Таблица 8. ВЫВОД ОСТАТКА
Уравнение регрессии имеет вид: y= 1,165+ 0,097x1 +0,001x2 . Индекс корреляции (R)=0,851 (табл.5). Коэффициент детерминации = 0,724. Следовательно, около 72% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов. Задание 3 Проверку значимости уравнения регрессии произведем на основе критерия Фишера. Значение F-критерия Фишера находится в таблице 6 и равен 48,636. Табличное значение при α=0,05 и k1 =2, k2 =37 составляет 3,252. Поскольку Fрас › Fтабл , то уравнение регрессии следует признать адекватным. Значимость коэффициентов уравнения регрессии оценим с использованием t-критерия Стьюдента. Расчетные значения для a1 и a2 приведены в таблице 7 и равны 4,883 и 2,848. Табличное значение найдем с помощью функции СТЬЮДРАСПОБР при α=0,05 и k=37. Оно составляет 2,026. Т.к. расчетные значения больше табличного, то коэффициенты уравнения регрессии значимы.
Задание 4 Коэффициент эластичности рассчитывается по формуле:
βj
= ∆j
= Таблица 9
Тогда Э1 (для X1 )=0,097*11,86/2,95=0,391 β1 =0,097*5,43/0,82=0,581 ∆1 =0,806*0,581/0,724=0,647. При изменении объема работ на 1% накладные расходы изменятся на 39%.При увеличении объема работ на 5,43 млн. руб. накладные расходы увеличатся на 476 тыс. руб. (0,581*0,82). Доля влияния объема работ в суммарном влиянии всех факторов составляет 64,7%. Таблица 10
Тогда Э2 =0,001*568,725/2,95=0,214 β2 =0,001*276,6/0,82=0,339 ∆2 =0,744*0,339/0,724=0,348. При изменении численности рабочих на 1% накладные расходы изменятся на 21%. При увеличении численности рабочих на 277 человек накладные расходы увеличатся на 280 тыс. руб. (276,6*0,82). Доля влияния численности рабочих в суммарном влиянии всех факторов составляет 35%. Задание 5
Проверим выполнение предпосылок МНК: · Отсутствие автокорреляции Отсутствие автокорреляции проверяется по d-критерию Дарбина - Уотсона:
d=1,46 (d1 =1,45 и d2 =1,59). Следовательно возникает неопределенность,
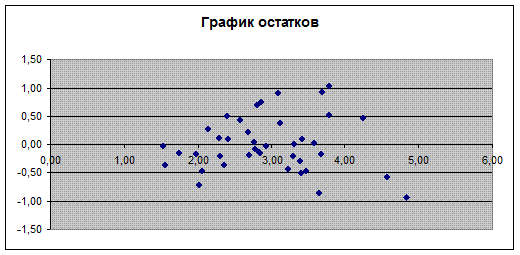
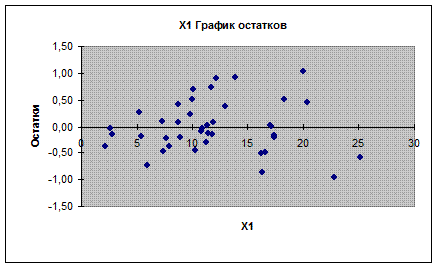
r=0,73 (rтабл =0,851), следовательно автокорреляция отсутствует. · Случайный характер остатков. Случайный характер остатков проверяется по графику. Как видно из графика в расположении точек Ei нет направленности, следовательно, Ei – случайные величины и применение МНК оправдано. · Средняя величина остатков или математическое ожидание равно нулю.
Так как расположение остатков на графике не имеет направленности, то они независимы от значений фактора x1 . · Остатки подчиняются нормальному закону распределения. · Проверка гомоскедастичности остатков: Гомоскедастичность остатков проверяется по тесту Голдфельда - Кванта. 1) Ранжируем наблюдение в порядке возрастания х. Делим их на две группы: с большим и меньшим x и для каждой группы определяем уравнение регрессии. Получаем следующие уравнения y=0,84+0,16x1 + 0,0006x2 и y=1,996+0,05x1 + 0,001x2 Рассчитываем остаточные суммы квадратов для каждой регрессии.
Вычисляются F- распределения. Fнабл.=S2ŷ /S1ŷ или Fнабл.= S1ŷ /S2ŷ из условий, что в числителе должна быть большая сумма квадратов. Fнабл. = S2ŷ /S1ŷ =2,67 Производится сравнение Fнабл. и Fтабл. 2,06<2,67(при k1 =40, k2 =18, α=0,05) следовательно, гетероскедастичность имеет место. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

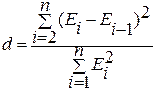 .
.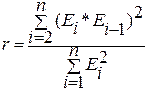
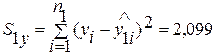 ,
,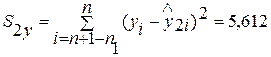 .
.