| Національний технічний університет України «КПІ»
Факультет Інформатики та Обчислювальної техніки
Кафедра Обчислювальної Техніки
Лабораторна робота №2-1
З курсу Алгоритми та Чисельні методи
Виконала:
Студентка 2-го курсу ФІОТ
Групи ІО-92
ГлуШко Ольга
З.к. №9204
Перевірив:
Флеров А.І.

Київ 2011
Вариант №4
Задание:
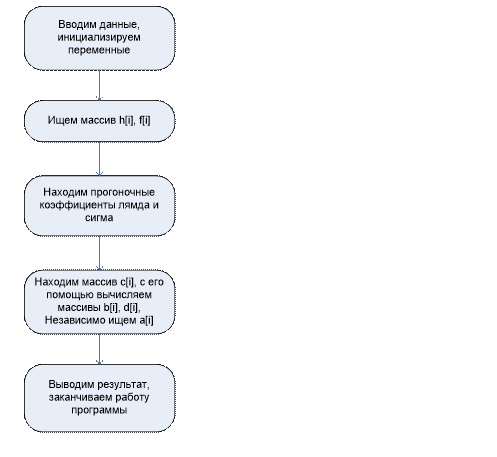
Выполнить аппроксимацию функции, заданной таблично, кубическим сплайном, разработать блок-схему и программу, оценить погрешность аппроксимации. Результаты представить в таблице вычислений: промежуточные значения вычисления по выбранной или заданной формуле метода, конечные результаты, погрешность вычисленного результата и предоставить формулы, которые были применены для вычисления.
| X
|
3.50
|
3.55
|
3.60
|
3.65
|
3.70
|
3.75
|
3.80
|
| Y
|
33.154
|
34.813
|
36.598
|
38.477
|
40.473
|
42.547
|
44.391
|
Использованные формулы
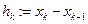
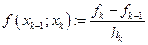
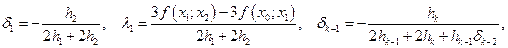
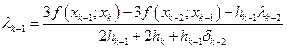
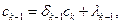
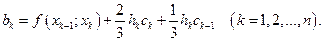
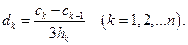
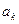 известны и равны известны и равны 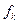 при любом при любом 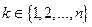
Т.к. значение первой (или второй) производной на границе неизвестно, то можно задать т.н. естественные граничные условия S''(A)=0, S''(B)=0, и получить естественный сплайн. Погрешность интерполяции естественным сплайном составляет O(h^2). Максимум погрешности наблюдается в окрестностях граничных узлов, во внутренних узлах точность интерполяции значительно выше. Погрешность сплайна 0,05*0,05=0,0025
Uses crt;
type massiv=array[0..6] of real;
const x:array[0..6] of real=
(3.50,3.55,3.60,3.65,3.70,3.75,3.80);
y:array[0..6] of real=(33.154, 34.813, 36.598, 38.477,
40.473, 42.547, 44.391);
var
a,b,c,d,sigma,lambda,h,f:massiv;
i,n,oo:integer;
begin
Clrscr;
n:=6;
writeln('array of h[i]');
for i:=1 to n do
begin
h[i]:= x[i]-x[i-1];
write(h[i]:0:3,' ');
end;
writeln;
writeln('array of f[i]');
for i:=1 to n do
begin
f[i]:=(y[i]-y[i-1])/h[i]; {nazvanie po starshemy Y}
write(f[i]:0:3,' ');
end;
writeln;
sigma[1]:=(-h[2])/(2*h[1]+2*h[2]);
lambda[1]:=(3*f[2]-3*f[1])/(2*h[1]+2*h[2]);
for i:=3 to n do
sigma[i-1]:=(-h[i])/(2*h[i-1]+2*h[i]+h[i-1]*sigma[i-2]);
for i:=3 to n do
begin
lambda[i-1]:=(3*f[i]-3*f[i-1]-h[i-1]*lambda[i-2]);
lambda[i-1]:=lambda[i-1]/(2*h[i-1]+2*h[i]+h[i-1]*sigma[i-2]);
end;
c[n]:=0;
for i:=n downto 1 do
c[i-1]:=sigma[i-1]*c[i]+lambda[i-1];
for i:=1 to n do
begin
b[i]:=f[i]+(2/3)*h[i]*c[i]+(1/3)*h[i]*c[i-1];
d[i]:=(c[i]-c[i-1])/(3*h[i]);
a[i]:=y[i];
end;
for i:=1 to n do
writeln ('g[',i,']=',a[i]:0:3,'+',b[i]:0:3,'*(x-',x[i]:0:3,')+',c[i]:0:3,'*(x-',
x[i]:0:3,')^2+',d[i]:0:3,'*(x-',x[i]:0:3,')^3');
readln;
end.

|