|
Система счисления – это способ представления чисел и соответствующие ему правила действия над числами. Разнообразные системы счисления, которые существовали ранее и существуют теперь, можно разделить на позиционные и непозиционные. Знаки, которые используются при записи чисел, называются цифрами.
В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает.
Примером непозиционной системы счисления является римская система (римские цифры). В римской системе в качестве цифр используются латинские буквы:
I V X L C в M
1 5 10 50 100 500 1000
Пример 1. Число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
Пример 2.
VI=5+1=6, а IV=5-1=4
Пример 3.
MCMXCVIII =1000+ (1000-100) + (-10+100) +5+1+1+1=1998
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием позиционной системы счисления.
Система счисления, применяемая в современной математике, является позиционной десятичной системой. Ее основание равно десяти, т.к. запись любых чисел производится с помощью десяти цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиционный характер этой системы легко понять при наличии любого многозначного числа. Например, в числе 333первая тройка означает три сотни, вторая – три десятка, а третья – три единицы.
Для записи чисел в позиционной системе счисления с основанием n нужно иметь алфавит из n цифр. Обычно для этого при n < 10 используют n первых арабских цифр, а при n > 10 к десяти арабским цифрам добавляют буквы. Вот примеры алфавитов нескольких систем:
| Основание
|
Название
|
Алфавит
|
| n=2
|
двоичная
|
0 1
|
| n=3
|
троичная
|
0 1 2
|
| n=8
|
восьмеричная
|
0 1 2 3 4 5 6 7
|
| n=16
|
шестнадцатеричная
|
0 1 2 3 4 5 6 7 8 9 A B C в E F
|
Если требуется указать основание системы, к которой относится число, то оно приписывается нижним индексом к этому числу. Например:
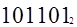 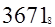 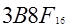
В системе счисления с основанием q (q-ичная система счисления) единицами разрядов служат последовательные степени числа q. q единиц какого-либо разряда образуют единицу следующего разряда. Для записи числа в q-ичной системе счисления требуется q различных знаков (цифр), изображающих числа 0,1,…,q-1. запись числа q в q-ичной системе счисления имеет вид 10.
Развернутой формулой записи числа называется запись в виде
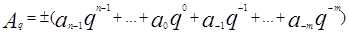
Здесь 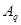 – само число, q – основание системы счисления, – само число, q – основание системы счисления, 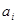 - цифры данной системы счисления, n – число разрядов целой части числа, m – число разрядов дробной части числа. - цифры данной системы счисления, n – число разрядов целой части числа, m – число разрядов дробной части числа.
Пример 4. получить развернутую форму десятичных чисел 32478; 26,387.
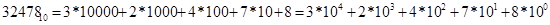
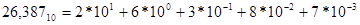
Пример 5. получит развернутую форму чисел
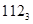 , , 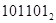 , , 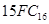 , , 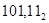
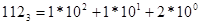
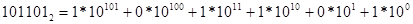
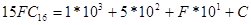
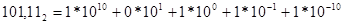
Обратите внимание, что в любой системе счисления ее основание записывается как 10.
Если все слагаемые в развернутой форме недесятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе, равное данному. По этому принципу производится перевод из недесятичной системы в десятичную.
Пример 6. Все числа из предыдущего примера перевести в десятичную систему.
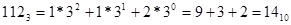
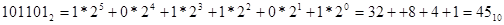
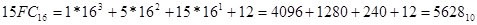
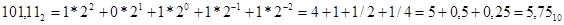
Задачи
№1
Какие числа записаны с помощью римских цифр:
MMMD, IV, XIX, MCXCIVII?
№2
Запишите год, месяц и число вашего рождения с помощью римских цифр.
№3
В старину на Руси широко применялась система счисления, отдаленно напоминающая римскую. С ее помощью сборщики податей заполняли квитанции об уплате податей. Для записи чисел употреблялись следующие знаки:
Звезда – тысяча рублей, колесо – сто рублей, квадрат – десять рублей,
Х – один рубль, I I I I I I I I I I – десять копеек, I – копейка.
Запишите при помощи старинной русской системы счисления сумму 3452 рубля 43 копейки.
№4
Какая сумма записана при помощи старинной русской системы счисления
 Х Х Х I I I I I I I I I I I I I Х Х Х I I I I I I I I I I I I I
№5
Придумайте свою непозиционную систему счисления и запишите в ней числа 45, 769, 1001.
№6
В некоторой системе счисления цифры имеют форму различных геометрических фигур. На рисунке приведены некоторые числа, записанные этой системе счисления:
 - 4 - 4  -190 -190
 - 6 - 6  - 1900 - 1900
 -19 -19
Какому числу соответствует следующая запись:

№7
Выполните действия и запишите результат римскими цифрами:
XXII-V; CV-LII; IC+XIX; MCM+VIII;
XX/V; X*IV; LXVI/XI; XXIV*VII.
№8
Какое количество обозначает цифра 8 в десятичных числах
6538, 8356, 87 и 831?
№9
Что вы можете сказать о числах 111 и I I I?
№10
Выпишите алфавит в 5-ричной, 7-ричной и 12-ричной системах счисления.
№11
Запишите первые 20 чисел натурального числового ряда в двоичной, 5-ричной, 8-ричной, 16-ричной системах счисления.
№12
Запишите в развернутом виде числа:
1) 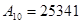 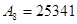 ; 2) ; 2) 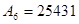 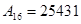
№13
Запишите в развернутом виде числа:
1) 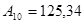 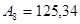 ; 2) ; 2) 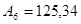 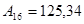
№14
Запишите в развернутой форме числа:
1) 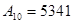 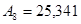 ; 2) ; 2) 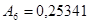 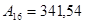
№15
Запишите десятичной системе счисления числа:
1) 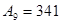 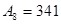 ; 2) ; 2) 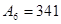 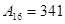
№16
Запишите в десятичной системе счисления числа:
1) 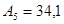 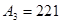 ; 2) ; 2) 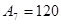 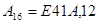
№17
Запишите десятичный эквивалент числа 110101, если считать его написанным во всех системах счисления – от двоичной до девятеричной включительно.
№18
Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 10, 21, 201, 1201?
№19
Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 403, 561, 666, 125?
№20
Какое минимальное основание должна иметь система счисления, если в ней могут быть записаны числа: 22, 964, 1010, А219?
№21
В каких системах счисления 10 – число нечетное?
№21
В каких системах счисления справедливы неравенства:
2*2=10, 2*3=11, 3*3=13?
Перевод десятичных чисел в другие системы счисления.
Перевод целых чисел
1. основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной системе счисления;
2. последовательно выполнять деление данного числа и получаемых неполных частых на основание новой системы счисления до тех пор, пока не получим неполное частное, меньшее делителя;
3. полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4. составить число в новой системе счисления, записывая его, начиная с последнего частного.
Пример 1. Перевести число 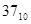 в двоичную систему. Для обозначения цифр используем символику: в двоичную систему. Для обозначения цифр используем символику: 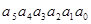
Перевод дробных чисел.
1. основание новой системы счисления выразить в десятичной системе и все последующие действия производить в десятичной системе счисления;
2. последовательно умножать данное число и полученные дробные части произведений на основание новой системы до тех пор, пока дробная часть не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;
3. полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
4. составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).
Пример 4. Перевести десятичное число 315,1875 в восьмеричную и шестнадцатеричную системы счисления.
Из рассмотренных выше примеров следует:
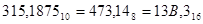 . .
Задачи
№23
Перевести целые числа из десятичной системы счисления в троичную:
1. 523; 65; 7000; 2307; 325
2. 12; 524; 76; 121; 56.
№24
Перевести целые числа из десятичной системы счисления в восьмеричную:
1. 856; 664; 5012; 6435; 78;
2. 214; 89; 998; 653; 111.
№25
Перевести десятичные дроби в двоичную систему счисления. В двоичной записи числа сохранить шесть знаков.
1. 0,654; 0,321; 0,6135; 0,9876;
2. 0,55; 0,333; 0,1213; 0,453.
№26
Перевести десятичные дроби в шестнадцатеричную систему счисления. В новой записи дроби сохранить шесть знаков
1. 0,745; 0,101; 0,8453; 0,3451;
2. 0,8455; 0,225; 01234; 0,455
№27
Перевести смешанные десятичные числа в троичную и пятеричную системы счисления, оставить пять знаков в дробной части нового числа:
1. 40,5; 34,25; 124,44;
2. 78,333; 225,52; 90,99.
№28
Перевести смешанные десятичные числа в двоичную и восьмеричную системы счисления, оставив пять знаков в дробной части нового числа:
1. 21,5; 432,54; 678,333;
2. 12,25; 97,444; 7896,2.
№29
Перевести из десятичной системы счисления следующие числа:
1. 345 - 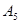 , 0,125 - , 0,125 - 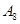 , 45,65 - , 45,65 - 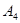 ; ;
2. 675 - 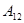 , 0,333 - , 0,333 - 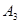 , 23,15. , 23,15.
№30
Перевести из десятичной системы счисления следующие числа:
1. 1,25 - 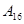 , 675 - , 675 - 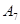 , 0,355 - , 0,355 - 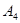 ; ;
2. 890 - 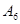 , 0,675 - , 0,675 - 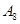 , 12,35 - , 12,35 - 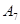
№31
Перевести из десятичной системы счисления следующие числа:
1. 425 - 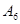 , 0,425 - , 0,425 - 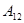 , 98,45 - , 98,45 - 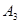 ; ;
2. 0,55 - 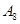 , 765 - , 765 - 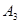 , 765,75 - , 765,75 - 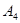 . .
№32
Перевести из десятичной системы счисления следующие числа:
1. 98 - 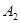 , 0,545 - , 0,545 - 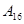 , 87,325 - , 87,325 - 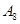 ; ;
2. 0,775 - 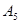 , 907 - , 907 - 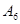 , 566,225 - , 566,225 - 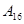
Системы счисления, используемые в ЭВМ (с основанием 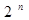 ) )
Для того чтобы целое двоичное число записать в системе счисления с основанием 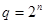 (4,8,16 и т.д.), нужно: (4,8,16 и т.д.), нужно:
1. данное двоичное число разбить справа налево на группы по n цифр в каждой;
2. если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов;
3. рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой системе счисления с основанием 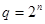 . .
Для того чтобы дробное двоичное число записать в системе счисления с основанием 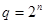 , нужно: , нужно:
1. данное двоичное число разбить слева направо на группы по n цифр в каждой;
2. если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов;
3. рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой системе счисления с основанием 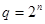 . .
Для того чтобы произвольное двоичное число записать в системе счисления с основанием 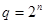 , нужно: , нужно:
1. данное двоичное число разбить слева и справа (целую и дробную части) на группы по n цифр в каждой;
2. если в последних правой и левой группах окажется меньше n разрядов, то их нужно дополнить нулями до нужного числа разрядов;
3. рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой системе счисления с основанием 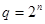 . .
Для того чтобы произвольное число, записанное в системе счисления с основанием 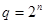 , перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления. , перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления.
Применительно к компьютерной информации часто используются системы счисления с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).
Пример 5. Перевести число 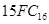 в двоичную систему. в двоичную систему.
Для решения задачи воспользуемся приведенной ниже двоично-шестнадцатеричной таблицей.
Двоично-шестнадцатеричная таблица
| 16
|
2
|
16
|
2
|
| 0
|
0000
|
8
|
1000
|
| 1
|
0001
|
9
|
1001
|
| 2
|
0010
|
A
|
1010
|
| 3
|
0011
|
B
|
1011
|
| 4
|
0100
|
C
|
1100
|
| 5
|
0101
|
D
|
1101
|
| 6
|
0110
|
E
|
1110
|
| 7
|
0111
|
F
|
1111
|
В одном столбце таблицы помещены шестнадцатеричные цифры, напротив, в соседнем столбце – равные им двоичные числа. Причем все двоичные числа записаны в четырехзначном виде (там, где знаков меньше четырех, слева добавлены нули).
А теперь проделаем следующее: каждую цифру в шестнадцатеричном числе 15FC заменим на соответствующую ей в таблице четверку двоичных знаков. Иначе говоря, перекодируем число 15FC по таблице в двоичную форму. Получается:
0001 0101 1111 1100
Если отбросить нули слева (в любой системе счисления они не влияют на значения числа), то получим искомое двоичное число. Таким образом:
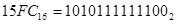
В справедливости этого равенства можно убедиться, производя тот же перевод через десятичную систему.
Пример 6. Перевести двоичное число 110111101011101111 в шестнадцатеричную систему.
Разделим данное число на группы по четыре цифры, начиная справа. Если в крайней левой группе окажется меньше четырех цифр, то дополним ее нулями.
0011 0111 1010 1110 1111
А теперь, глядя на двоично-шестнадцатеричную таблицу, заменим каждую двоичную группу на соответствующую шестнадцатеричную цифру.
3 7 А E F
Следовательно:
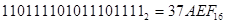 
Пример 7. Перевести смешанное число 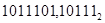 в шестнадцатеричную систему. в шестнадцатеричную систему.
Решение
Перевод дробных чисел производится аналогично. Группы по четыре двоичных знака выделяются от запятой как влево, так и вправо. Поэтому:
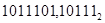 = 0101 1101, 1011 1000 = = 0101 1101, 1011 1000 = 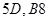 . .
Связь между двоичной и восьмеричной системами устанавливается аналогично. В этом случае используется двоично-восьмеричная таблица, приведенная ниже. Каждой восьмеричной цифре соответствует тройка двоичных цифр.
Двоично-восьмеричная таблица
| 8
|
2
|
| 0
|
000
|
| 1
|
001
|
| 2
|
010
|
| 3
|
011
|
| 4
|
100
|
| 5
|
101
|
| 6
|
110
|
| 7
|
111
|
Пример 8. Перевести смешанное число 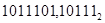 в восьмеричную систему. в восьмеричную систему.
Решение
Группы по три двоичных знака выделяются от запятой как влево, так и вправо. Затем производится перекодировка по таблице:
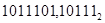 = 001 011 101, 101 110 = = 001 011 101, 101 110 = 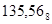 . .
Задачи
№33
Перевести двоичные числа в восьмеричную систему счисления:
1. 110000110101; 1010101; 0,1010011100100; 0,1111110001;
2. 0,1001111100000; 0,1100010; 11100001011001; 1000010101.
№34
Перевести двоичные числа в шестнадцатеричную систему счисления:
1. 11011010001; 111111111000001; 0,0110101; 0,11100110101;
2. 10001111010; 100011111011; 0,101010101; 01100110011.
№35
Перевести смешанные двоичные числа в восьмеричную и шестнадцатеричную системы:
1. 100010,011101; 1111000000,101; 101010,111001; 100011,111;
2. 101111,01100; 100000111,001110; 101010,0010; 1100011,11.
№36
Перевести восьмеричные числа в двоичную систему счисления:
1. 256; 0,345; 24,025; 0,25;
2. 657; 76,025; 0,344; 345,77.
№37
Перевести шестнадцатеричные числа в двоичную систему счисления:
1. 1АС7; 0,2D1; 2F,D8C; F0C,FF;
2. FACC; 0,FFD; FDA,12F; DDFF,A/
№38
Перевести числа из шестнадцатеричной системы в восьмеричную:
1. A45; 24A,9F; 0,FDD5; F12,0457$
2. A24,F9; 54A; 0,DFD3; 12D,567/
№39
Перевести числа из восьмеричной системы счисления в шестнадцатеричную:
1. 774; 765,25; 0,5432; 654,763;
2. 665; 546,76; 0,7654; 432,347.
№40
Перевести следующие числа:
1.  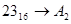 ; ; 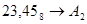 ; ; 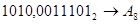 ; ; 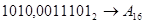 ; ;
2. 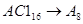 ; ; 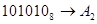 ; ; 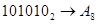 ; ; 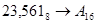
№41
Перевести следующие числа:
1. 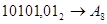 ; ; 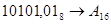 ; ;
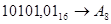 ; ; 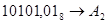
2. 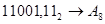 ; ; 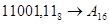 ; ;
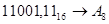 ; ; 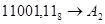
№42
Перевести следующие числа:
1. 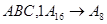 ; ; 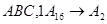 ; ;
2. 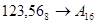 ; ; 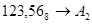 ; ;
3. 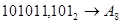 ; ; 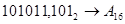 ; ;
4. 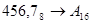 ; ; 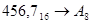 ; ;
№43
Опишите четверичную систему. Постройте двоично-четверичную таблицу.
№44
Перевести следующие числа:
1. 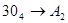 ; ; 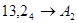 ; ; 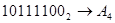 ; ; 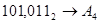 ; ;
2. 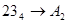 ; ; 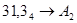 ; ; 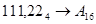 ; ; 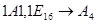 . .
№45
Перевести следующие числа:
1. 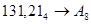 ; ; 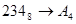 ; ; 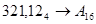 ; ; 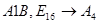 ; ;
2. 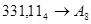 ; ; 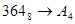 ; ; 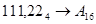 ; ; 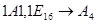 . .
Арифметика в позиционных системах счисления.
Любая позиционная система счисления определяется основанием системы, алфавитом и правилами выполнения арифметических операций. В основе правил арифметики лежат таблицы сложения и умножения однозначных чисел. Например, таблицы сложения и умножения в пятеричной системе счисления выглядят так:
Пятеричная таблица сложения пятеричная таблица умножения
| +
|
0
|
1
|
2
|
3
|
4
|
| 0
|
0
|
1
|
2
|
3
|
4
|
| 1
|
1
|
2
|
3
|
4
|
10
|
| 2
|
2
|
3
|
4
|
10
|
11
|
| 3
|
3
|
4
|
10
|
11
|
12
|
| 4
|
4
|
10
|
11
|
12
|
13
|
| 
|
1
|
2
|
3
|
4
|
| 1
|
1
|
2
|
3
|
4
|
| 2
|
2
|
4
|
11
|
13
|
| 3
|
3
|
11
|
14
|
22
|
| 4
|
4
|
16
|
22
|
31
|
|