|
Дано:
треугольник с вершинами в точках А [4; 0] B [3; 20]
и C
[5; 0].
Найти:
a) Уравнение прямой АВ
;
b) Уравнение высоты С
D
, проведенной к стороне АВ
;
c) Уравнение прямой СЕ
, параллельной стороне АВ;
d) Площадь треугольника АВС
Решение:
А) Уравнение прямой АВ
найдем по формуле:
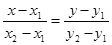 , где , где
X
1
,
Y
1
– координаты первой точки,
X
2
,
Y
2
– координаты второй точки.
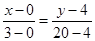
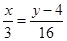
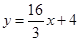
В) Уравнение высоты С
D
найдем, используя следующий алгоритм:
1. Найдем угловой коэффициент[1]
, используя условие перпендикулярности прямых[2]
:
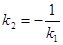 , где , где
K
1
– угловой коэффициент прямой АВ
K2
– угловой коэффициент прямой С
D
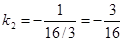
2. Найдем уравнение прямой с угловым коэффициентом k
2
, проходящая через точку С
[5; 0]:
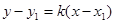 , где , где
X
1
,
Y
1
– координаты точки,
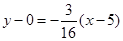
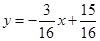
C) Уравнение прямой СЕ
найдем, используя следующий алгоритм:
1. Найдем угловой коэффициент, используя условие параллельности прямых:
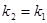 , где , где
K
1
– угловой коэффициент прямой АВ
K
2
– угловой коэффициент прямой СЕ
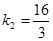
2. Найдем уравнение прямой с угловым коэффициентом k2
, проходящая через точку С
[5; 0]:
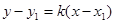 , где , где
X
1
,
Y
1
– координаты точки,
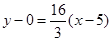
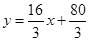
D) Найдем площадь треугольника по формуле:
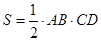
1. Найдем длину стороны АВ
по формуле:
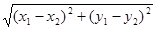 , где , где
X
1
,
Y
1
– координаты точки А
,
X
2
,
Y
2
– координаты точки В
,
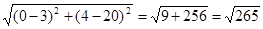
2. Найдем длину стороны СD по формуле:
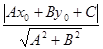 , где , где
X
0
,
Y
0
– координаты точки С
,
А,
B
,
C
– коэффициенты прямой АВ
(Ах+Ву+С – уравнение прямой).
Уравнение прямой АВ 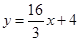 или
или 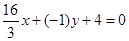
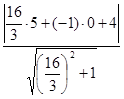
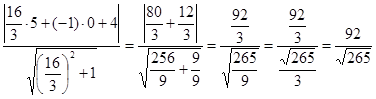
3. Найдем площадь S:
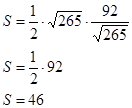
[1]
Угловой коэффициент прямой — коэффициент k
в уравнении y = kx + b
прямой на координатной плоскости
[2]
Высота треугольника (С
D
)— перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону (AB
)
|