|
 Федеральное агентство по образованию Российской Федерации Федеральное агентство по образованию Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
Контрольная работа
по дисциплине
«Управление техническими системами»
2008
Содержание
Модель «спроса-предложения» рыночного саморегулирования…………………………......3
Методы принятия решения в условиях дефицита информации……………………………...5
Деловые (хозяйственные) игры…………………………………………………………............6
Задача……………………………………………………………………………………………..7
Список литературы…………………………………………………………………………….12
Модель «спроса-предложения» рыночногосаморегулирования.
В рыночных условиях спрос - это готовность потребителя приобретать услуги в допустимом количестве Q и по данной цене Рс. Чем ниже цена Рс, тем больше сервисных или транспортных услуг может быть приобретено потребителем (1,рис.1).

Рисунок-1. Регулирование цены и объемов транспортных и сервисных услуг в рыночных условиях и свободной конкуренции:
1- исходная линия спроса;
2- исходная линия предложения;
3-измененная линия предложения;
4- измененная линия спроса
Предложение - желание перевозчика или сервисного предприятия осуществлять транспортные услуги или техническое обслуживание в данном объеме Q и при данной цене предложения Рп. Чем выше цена, тем больше предложений Q сервисных предприятий и перевозчиков (2,рис.1).
Зона левее точки равновесия 0, заключенная между линиями спроса и предложения 1 и 2, - это зона эффективных цен для СТО или перевозчика и потребителя.
Правее точки равновесия 0 находится зона неэффективной работы для стороны, предлагающей услуги (перевозки или сервис), так как предлагаемые ей цены при увеличении объема перевозок или услуг (линия спроса 1 правее точки О) ниже затрат на эти перевозки или сервис (линия предложения 2). Например, в точке А объем транспортных услуг (сервиса) QA
по цене РА
не будет реализован, так как фактическая цена (тариф) ниже затрат или себестоимости услуг, т.е. Р0
>РА
или Pп>Pc - цена предложения выше цены спроса.
В этой ситуации в реальных условиях возможны несколько решений, в том числе:
а) дополнительный объем сервисных услуг или перевозок
ΔQ=QА
-QО
не будет реализован, и рынок автоматически вернется, по крайней мере, в точку равновесия 0 или левее ее;
б) сторона, предоставляющая услуги, за счет внутренней экономии снижает тарифы (новая линия предложения 3 на рис.1) до уровня РА
. В этом случае точка равновесия перемещается в точку А (для спроса и предложений 1 и 3), а эффективная для стороны, предоставляющей услуги, зона увеличивается;
в) потребители идут на увеличение возможной цены на перевозки (линия спроса 4 на рис. 1) до Рв. При этом объем услуг QA
может быть реализован по цене РВ
>РА
;
г) или реализуется комбинация этих решений;
Таким образом, управляющим для этой системы сигналом является соотношение спроса и предложения при необходимом объеме транспортных или сервисных услуг
ΔP=Pc(Qi)-PП
(Qi) (1)
Включение в управление обратной связи позволяет дать прогноз работы системы, для которой могут происходить резкие изменения условий работы, что характерно для мелкого бизнеса. Мелкий бизнес (предоставление сервисных услуг, челночная торговля и др.) характерен сравнительно небольшим оборотом средств и малой массой прибыли. Поэтому изменение внешних условий (налогов, таможенных сборов, иен на оборудование и др.) существенно сказывается на рынке, обслуживаемом мелким бизнесом.
рассмотрим влияние значительного изменения внешних условий на объемы и цены услуг (рис.2).

Рисунок-2. Прогноз
изменения насыщения рынка и цен:
1, 2 - исходное положение,*
3 - линия предложения при сохранении объема торговли
на уровне Qo;
4 -линия спроса при компенсации дополнительных затрат стороны, предоставляющей услуги.
Исходная ситуация (до изменения внешних факторов) фиксируется линиями спроса (1,рис.2) и предложения (2, рис. 2). Дополнительное налогообложение СТО ремонтных мастерских, мелких перевозчиков, "челноков" приведет к росту цен (линии предложения 3) и смещению точки равновесия влево до О1
. Это приведет к росту цен Р1
>Po и одновременному сокращению объемов торговли или предоставления других услуг, т.е. сокращению насыщения рынка Qi<Q0
и возможно, к дефициту.
Если потребители стремятся сохранить объем приобретаемых услуг или товаров (Q0
), то это неизбежно приведет к еще большему росту цен Р2
> Р1
>Po, чем при относительном дефиците ( линия спроса 4).
МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЯ В УСЛОВИЯХ ДЕФИЦИТА ИНФОРМАЦИИ.
Как правило, при принятии инженерных, управленческих и других решений полная информация о состоянии системы, внешних условиях и последствиях принимаемых решений отсутствует.
Американские специалисты утверждают, что 80% решений принимается при наличии только 20% информации об управляемой, системе.
Например, принимая решение о числе постов на станции технического обслуживания, можно только предполагать о потенциальном числе клиентов и их распределении по часам суток, дням недели , месяцам года и т.п.
Аналогичная ситуация с числом возможных требований на конкретный вид ремонта автомобиля в течение "завтрашнего дня", возможности выхода или невыхода на работу конкретного специалиста или рабочего и т.д. Строго говоря полную информацию можно получить только после свершения того или иного события (например, отказы уже произошли), когда необходимость в упреждающем решении отпала, а система перешла в режим реактивного управления.
Поэтому при управлении необходимо уметь теми или иными способами восполнить или компенсировать дефицит информации. Такими способами укрупненно являются:
1) Сбор дополнительной информации, и ее анализ. Очевидно, это возможно, если система располагает определенным резервом времени и средств.
2) Использование опыта аналогичных предприятий или решений. При этом важно располагать банком решений или иметь надежный доступ к нему. Кроме того, опыт других не может быть использован без корректирования.
3) Использование коллективного мнения специалистов или экспертизы.
4) Применение специальных инструментальных методов и критериев, основанных на теории игр.
5) Использование имитационного моделирования, которое воспроизводит производственные ситуации, близкие к реальным, и ряд других методов.
ДЕЛОВЫЕ (ХОЗЯЙСТВЕННЫЕ) ИГРЫ
Возможность оценивать варианты решений, изменять входные данные, при необходимости упрощать ситуации позволяет использовать имитационное моделирование при обучении персонала и оценке его квалификации. Например, при исследовании производительности СМО (постов, участков) участником деловой игры может реализовываться определенная дисциплина очереди: пропускать в первую очередь требования на ремонт автомобилей, дающих наибольший доход, или требования с малой продолжительностью обслуживания. В многоканальных системах возможно перераспределение требований или исполнителей по постам.
С помощью комбинации ряда подобных моделей конструируют имитационные модели зоны, участка, цеха и предприятия. Имитационные модели используются при проведении деловых игр.
Деловые (хозяйственные) игры - это метод имитации принятия управленческих решений в различных производственных ситуациях. При этом обучающемуся создают ту или иную управленческую или производственную ситуацию, из которой необходимо найти рациональный выход, т.е. принять решение. Критерием является степень приближения решения к оптимальному, (которое известно организаторам деловых игр) и время принятия решения. Деловые игры проводятся по определенным правилам, регламентирующим поведение участников, их взаимодействие, критерии эффективности. В роли датчиков, имитирующих реальные производственные ситуации, выступают ПЭВМ (человеко-машинная система), наборы карточек случайных событий или организаторы деловой игры.
В деловых играх участвуют специалисты, которые в создаваемых имитационной моделью "производственных ситуациях" принимают решения.
Деловые игры используются при обучении и оценке персонала и исследовании сложных производственных систем.
При обучении персонала они используются для иллюстрации, разъяснения определенных закономерностей и понятий и закрепления знаний; для программного и целевого обучения определенных специалистов, например, диагноста, оператора ЦУП и др; для тренировки специалистов непосредственно на производстве. При обучении персонала деловые игры, как правило, разворачиваются в реальном масштабе времени. При исследовании, производственных ситуации применяется сжатый масштаб времени.
Деловые игры позволяют осуществлять предварительный отбор кадров, так как при этом можно оценить способности, профессиональные навыки и знания кандидатов на определенные рабочие места и должности специалистов и управленцев.
Задача.
Рассчитать значения и построить график функции w(t) – параметр потока замен машин при случайном списании по достижении машиной предельного состояния и мгновенной замене ее на новую.
Расчет функции w(t) выполнить для значений t=1,2,3… ti, где для ti выполняется условие:
/w(ti)-w(ti-1)/<0,01 и /w(ti)-wп/<0,01
где wп – предельное значение функции w(t) при увеличении времени t.
В расчетах использовать предложение о нормальном распределении срока службы машин с заданными значениями параметром m = 4,0 (математическое ожидание) и s = 1,1 (среднеквадратическое отклонение).
Для парка, в котором имеется N машин:
а) рассчитать точное значение математического ожидания, т. е. среднего числа машин, необходимых для замены за 6,5 лет работы от начала существования парка машин;
б) определить приближенное значение математического ожидания числа машин, необходимых для замены за период времени работы парка от а1
= 7 до b1
= 12, используя линейную аппроксимацию функции w(t) по расчетным значениям;
в) определить приближенное значение математического ожидания числа машин, необходимых для замены в установившемся режиме работы парка за период времени от а2
= 20 до b2
= 30 и оценить максимальную погрешность этого значения.
Значение числа машин в парке N = (7 + 30) = 37
Решение:
1. Расчет значений функции параметр потока замен
Проведем расчет значений функции параметр потока замен w(t).
Пусть заданы значения параметров нормального распределения m = 4,0 и s = 1,1. Тогда математическое ожидание срока службы машин tср
= m = 4,0.
Определяем предельное значение wп
функции w(t) при увеличении времени t:
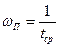 (1) (1)
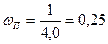
Для расчета значений функции w(t) воспользуемся формулой:
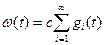 (2) (2)
где 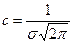 (3) (3)

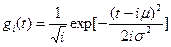 (4) (4)
Результаты расчета представим в виде таблицы. Значения gi
(t), меньше 10-3
, не входят в сумму и указаны в таблице, что бы показать, что при данном значении t дальнейшее увеличение значения t не требуется.
Таблица 1.
| t
|
i
|
gi(t)
|
Σgi(t)
|
w(t)
|
| 1
|
1
|
3
|
4
|
5
|
| |
1
|
0,02425801
|
0,02425801
|
|
| |
2
|
2,836E-05
|
0
|
|
| |
|
|
0,02425801
|
0,009
|
| 2
|
1
|
0,1914952
|
0,1914952
|
|
| |
2
|
0,0004161
|
0
|
|
| |
3
|
6,0176E-07
|
0
|
|
| |
|
|
0,1914952
|
0,07
|
| 3
|
1
|
0,66151466
|
0,66151466
|
|
| |
2
|
0,00403858
|
0,00403858
|
|
| |
3
|
8,2415E-06
|
0
|
|
| |
|
|
0,66555323
|
0,242
|
| 4
|
1
|
1
|
1
|
|
| |
2
|
0,0259299
|
0,0259299
|
|
| |
3
|
8,5694E-05
|
0
|
|
| |
|
|
1,0259299
|
0,372
|
| 5
|
1
|
0,66151466
|
0,66151466
|
|
| |
2
|
0,11013177
|
0,11013177
|
|
| |
3
|
0,00067647
|
0
|
|
| |
4
|
1,8633E-06
|
0
|
|
| |
|
|
0,77164643
|
0,28
|
| 6
|
1
|
0,1914952
|
0,1914952
|
|
| |
2
|
0,30943109
|
0,30943109
|
|
| |
3
|
0,00405427
|
0,00405427
|
|
| |
4
|
1,631E-05
|
0
|
|
| |
|
|
0,50498056
|
0,183
|
| 7
|
1
|
0,02425801
|
0,02425801
|
|
| |
2
|
0,57511506
|
0,57511506
|
|
| |
3
|
0,01844739
|
0,01844739
|
|
| |
4
|
0,00011612
|
0
|
|
| |
5
|
3,8437E-07
|
0
|
|
| |
|
|
0,61782046
|
0,224
|
| 8
|
1
|
0,00134472
|
0,00134472
|
|
| |
2
|
0,70710678
|
0,70710678
|
|
| |
3
|
0,06372598
|
0,06372598
|
|
| |
4
|
0,00067236
|
0
|
|
| |
5
|
3,0343E-06
|
0
|
|
| |
|
|
0,77217748
|
0,28
|
| 9
|
1
|
3,262E-05
|
0
|
|
| |
2
|
0,57511506
|
0,57511506
|
|
| |
3
|
0,1671313
|
0,1671313
|
|
| |
4
|
0,00316649
|
0,00316649
|
|
| |
5
|
2,0303E-05
|
0
|
|
| |
|
|
0,74541285
|
0,271
|
| 10
|
1
|
3,4627E-07
|
0
|
|
| |
2
|
0,30943109
|
0,30943109
|
|
| |
3
|
0,33278111
|
0,33278111
|
|
| |
4
|
0,01212901
|
0,01212901
|
|
| |
5
|
0,00011516
|
0
|
|
| |
6
|
5,6046E-07
|
0
|
|
| |
|
|
0,6543412
|
0,238
|
| 11
|
1
|
1,6085E-09
|
0
|
|
| |
2
|
0,11013177
|
0,11013177
|
|
| |
3
|
0,50305932
|
0,50305932
|
|
| |
4
|
0,03778694
|
0,03778694
|
|
| |
5
|
0,00055367
|
0
|
|
| |
6
|
3,5985E-06
|
0
|
|
| |
|
|
0,65097802
|
0,236
|
| 12
|
1
|
3,2698E-12
|
0
|
|
| |
2
|
0,0259299
|
0,0259299
|
|
| |
3
|
0,57735027
|
0,57735027
|
|
| |
4
|
0,0957476
|
0,0957476
|
|
| |
5
|
0,00225642
|
0,00225642
|
|
| |
6
|
2,0131E-05
|
0
|
|
| |
|
|
0,70128418
|
0,255
|
| 13
|
1
|
2,9087E-15
|
0
|
|
| |
2
|
0,00403858
|
0,00403858
|
|
| |
3
|
0,50305932
|
0,50305932
|
|
| |
4
|
0,19732577
|
0,19732577
|
|
| |
5
|
0,00779474
|
0,00779474
|
|
| |
6
|
9,813E-05
|
0
|
|
| |
|
|
0,71221841
|
0,259
|
На рисунке 1 представлен график функции w(t). Точками показаны рассчитанные значения функции от t = 1 до 13 с шагом h = 1.

График функции w(t) дает наглядное представление об изменении во времени вероятности замены машины. Чем больше значение функции при данном значении аргумента (времени), тем больше вероятность замены машины в ближайшей окрестности от этого значения времени.
2. Расчет среднего числа машин, необходимых для замены в парке за данное время.
Проведем расчет среднего числа машин, необходимых для замены в парке из N машин за время t = 6,5 лет. Результаты расчетов поместим в таблицу 2.
Таблица 2.
| i
|
iµ
|
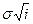
|

|

|
| 1
|
4
|
1,1
|
2,273
|
0,98819
|
| 2
|
8
|
1,556
|
-0,964
|
0,168
|
| 3
|
12
|
1,905
|
-2,887
|
0,00213
|
Ω(t) = Ф(zi
) =1,158
Значение функции «интеграл вероятностей» Ф(zi
) определяется по таблице приложения 1 с помощью линейной интерполяции.
При N = 37 за это время в парке потребуется в среднем машин для замены:
Н(0,6,5)=37*1,158=43
3. Расчет приближенного среднего значения числа замен машин в парке с использованием линейной аппроксимации параметра потока замен.
Рассчитаем приближенное значение математического ожидания числа замен машин в парке, пользуясь значениями функции w(t) и линейной аппроксимацией этой функции.
Пусть заданы нижняя граница интервала а1
= 7 и верхняя граница b1
= 12.
Тогда для одного места в парке приближенное значение среднего числа замен на этом интервале при шаге h = 1 будет:
Ω(7,12)=1{0,5[w(7)+w(12)]+w(8)+w(9)+w(10)+w(11)}=0,5(0,224+0,255)+0,28+0,271+0,238+0,236=1,265
При числе машин в парке N = 37 для замен потребуется в среднем машин:
H(7,12)=37×1,265=47
4. Вычисление среднего числа замен в парке при больших значениях времени.
Вычислим приближенное значение математического ожидания числа замен машин в парке при больших значениях времени t в установившиемся режиме, когда можно считать значение функции w(t) постоянным и равным wп
.
Если заданы нижняя граница интервала а2
= 20 и верхняя граница b2
= 30, то отклонение и, следовательно, погрешности при замене значений функции w(t) установившимся значением wп
, будет меньше 0,01.
При тех же значениях m = 4,0 и N = 37 предельное значение параметра потока замен
wп
= 0,25 и среднее число замен на данном интервале времени получим:
Ω(20,30)=0,25×(30-20)=2,5
Затем вычислим среднее число замен машин в парке:
H(6,13)=37×2,5=92,5
Список литературы
1. Кузнецов Е.С. Управление техническими системами. - М.: МАДИ (ГТУ), 2003, 248 с.
2. Техническая эксплуатация автомобилей: Учебник для ВУЗов / под ред. Кузнецова Е.С. - М.: Наука (4-е издание, переработанное и дополненное), 2001.
3. Лохов А.Н. Организация управления на автомобильном транспорте. Опыт, проблемы, перспективы. - М: Транспорт, 2001.
4. Кузнецов Е.С. Управление технической эксплуатацией автомобилей. Изд. 2-е переработанное и дополненное. - М.: Транспорт, 1990.
5. Бусленко Н.П. Моделирование сложных систем. - М.: Наука, 1978, 356 с.
6. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. - М.: Наука, 2001.
7. Прудовский Б.Д., Ухарский В.Б. Управление технической эксплуатацией автомобилей по нормативным показателям. - М.: Транспорт, 1990.
|