| Федеральное агентство по образованию
ГОУ ВПО «Российский государственный профессионально-педагогический университет»
Машиностроительный институт
Кафедра механики
Расчетно-графическая работа №1
«Структурный анализ зубострогального механизма»
030502.08.09.08 ПЗ
2009
Анализ кинематических пар, обозначенных на схеме буквами (см. рис. 1), сведен в таблицу 1.
Таблица 1
Анализ кинематических пар механизма
| Кинематич.
пара
|
О
|
А
|
А1
|
О1
|
В
|
С
|
Д
|
| Звенья,
Образующие
пару
|
0-1
|
1-2
|
2-3
|
3-0
|
3-4
|
4-5
|
5-0
|
| Класс пары
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
| Название
|
вращ.
|
вращ.
|
пост.
|
вращ.
|
вращ.
|
вращ.
|
пост.
|
Таким образом, n
= 5, р5
= 7, р4
= 0
Степень подвижности механизма определяется по формуле Чебышева:
W
= 3
n
– 2
p
5
–
p
4
,
где n – число подвижных звеньев,
р5
– число кинематических пар 5-го класса,
р4
– число кинематических пар 4-го класса
Следовательно, степень подвижности механизма будет равна: W
= 3*5-2*7-0 = 1
Вывод
: рассматриваемый механизм содержит один механизм первого класса, состоящий из входного звена (кривошипа) и стойки.
Разложение механизма на структурные составляющие (группы Ассура и механизм I класса)
Структурные составляющие механизма
а – группа Ассура II класса 2-го вида
б – группа Ассура II класса 3-го вида
в – механизм I класса
В итоге получаем следующую структурную формулу механизма:
I
->
II
3
->
II
2
Т.е. механизм образован присоединением к механизму I класса группы Ассура II класса 2-го вида.
Следовательно, делаем вывод: рассматриваемый механизм является механизмом II класса.
Построение плана положений механизма
План положений механизма строится с использованием масштабного коэффициента, начиная с разметки положения неподвижных шарниров и направляющих. Под масштабным коэффициентом
понимают отношение какой-либо физической величины к отрезку, изображающему эту физическую величину на плане.
μ
L
=Фактическая длина звена (м)/Длина отрезка на плане (мм)
Построение плана положений необходимо начинать с положения, в котором начинается рабочий ход механизма (одно из двух крайних положений, которое в дальнейшем будем называть нулевым
). Крайнее положение определяют по траектории движения исполнительного (выходного) звена, совершающего возвратное движение: скорость его в крайних положениях равна нулю, так как меняется направление движения.
В том случае, когда цикл движения механизма включает рабочий и холостой ход, положения рабочего хода определяются по заданному направлению силы полезного сопротивления, которая действует против движения выходного звена.
Если механизм не имеет холостого хода, т.е. при прямом и при обратном движениях выходного звена совершается полезная работа, то за нулевое можно принять любое из крайних положений.
Для определенных механизмов крайнее положение определяется легко: когда кривошип составляет с кулисой прямой угол или когда кривошип и шатун располагаются на одной прямой, для других - крайние положения следует определять подбором, контролируя определением скорости выходного звена.
Построив нулевое положение механизма, строят еще как минимум пять промежуточных положений. Для этого круговую траекторию конца кривошипа делят на шесть частей и нумеруют соответствующие положения в направлении вращения кривошипа. Остальные звенья в каждом из положений механизма строят последовательно засечками их длин, учитывая принятый масштабный коэффициент.
Следует учесть, что план положений должен включать оба крайних положения
механизма
, поэтому, если второе крайнее положение не вошло в число построенных шести, его строят дополнительно.
Одно из положений механизма, как правило, на рабочем ходу (лучше то, для которого будет проводиться силовой анализ) выделяется основными линиями, остальные изображаются контурными.
На плане положений при необходимости может быть определена траектория движения любой точки механизма, для чего последовательные положения выбранной точки соединяются плавной кривой.
Для механизма построен план семи положений. Масштабный коэффициент плана положений μ
L
=0,0038м/мм
. Размеры звеньев механизма равны
LOA
=0,15м,
LBC
=0,65м,
LBO
1
=0,65м
.
Точки О
и В
расположены на одной горизонтали на расстоянии 0,4м, и расстояние от точки О
до оси ползуна также равно 0,4м.
Сила полезного сопротивления направлена вверх, следовательно, рабочий ход ползуна механизма соответствует его движению вниз, поэтому нулевым будем считать верхнее крайнее положение ползуна. Второе крайнее положение механизма (нижнее), обозначено индексом k
.
Размещая нагрузочную диаграмму F
ПС
=f
(S
D
)
таким образом, чтобы перемещения ползуна (SD
) на диаграмме и плане положений соответствовали друг другу, мы сможем легко определить значение силы полезного сопротивления (F
ПС
) для любого положения механизма. Эти силы будут учитываться в расчете приведенного момента сил, при проектировании маховика в разделе «Динамика механизмов».
Для выполнения силового анализа следует выбрать одно из положений механизма, в котором сила сопротивления имеет наибольшее значение. Поэтому и план ускорений строится именно для этого положения. Максимальное значение силы полезного сопротивления Fmax
для нашего примера приходится на первое положение механизма.
Определение скоростей точек и угловых скоростей звеньев
План скоростей строится последовательно для отдельных структурных составляющих механизма в порядке, соответствующем синтезу механизма. Последовательность построения плана скоростей для одного положения механизма:
· Определяется скорость точки кривошипа, к которой присоединена первая группа Ассура, и строится вектор скорости этой точки в масштабе μ
v
из точки Р
, называемой полюсом плана скоростей. Конец вектора обозначается той же буквой (только строчной), что и соответствующая точка на плане положений.
·
Составляются векторные уравнения абсолютных скоростей точек в виде суммы переносной и относительной скоростей. В качестве переносного принимается движение точки, скорость которой известна, а относительное движение определяется в связи с этой точкой. Полученные уравнения решаются графически с использованием уже построенного вектора и известных направлений относительных скоростей.
·
Определяются истинные значения абсолютной и относительной скоростей рассматриваемой точки с помощью масштабного коэффициента.
·
Определяются величины и направления угловых скоростей звеньев, совершающих вращательное и плоскопараллельное движение, с помощью найденных относительных скоростей.
·
С помощью принципа подобия в плане скоростей, определяется скорость той точки данной группы Ассура, к которой свободным элементом кинематической пары присоединена следующая структурная группа, и строится вектор скорости этой точки на плане.
В таком же порядке строится план скоростей, и определяются все кинематические параметры для последующих групп Ассура.
По заданию кривошип вращается по часовой стрелке с угловой скоростью ω1
=9.8с-1
.
Скорость точки А
, принадлежащей оси шарнира, т.е. одновременно концу кривошипа и камню кулисы, равна
VA
=
ω
1
*
LOA
= 9.8
c
-1
*0.15м = 1.5м/с
и направлена перпендикулярно положению звена ОА в сторону, соответствующую угловой скорости. Выбрав полюс Р и величину отрезка Ра, Изображающего скорости точки А
(в данном примере Ра= 40мм), построим этот вектор и определим масштабный коэффициент.
μ
v
=
VA
/ Ра = 1,5мс-1
/ 100мм = 0,015мс-1
/ мм.
Рассмотрим группу Ассура, присоединенную к кривошипу и состоящую из звеньев 2 и 3, т.е. из кулисы ВС
и камня А
. Скорости точек А
и В
известны: скорость точки А
только что найдена, а скорость точки В равна нулю, так как она одновременно принадлежит и стойке. Следовательно, мы можем определить скорость точки, принадлежащей средней кинематической паре этой группы. Обозначим эту точку буквой А'
, поскольку на плане положений она совпадает с точкой А
, но принадлежит другому звену – кулисе ВС
. Составим два векторных уравнения, связывающих скорость точки А'
, с известными скоростями точек А
и В
:
→ → → →
VA
'
=
VA
+
VA
'
A
; (
VA
'
A
||
BC
)
→ → → →
VA
'
=
VB
+
VA
'
B
; (
VA
'
B
┴
BC
,
VB
= 0)
,
где VA
'
A
– вектор скорости в относительном поступательном движении точки А'
кулисы относительно точки А
камня (направление ее известно – вдоль кулисы ВС
, так как поступательная пара между звеньями 2 и 3 никакого другого относительного движения не допускает);
V
A
'
B
– вектор скорости в относительном вращательном движении точки А'
относительно точки В
(направление ее также известно – перпендикулярно кулисе ВС
, так как скорость во вращательном движении всегда перпендикулярна радиус - вектору точки)
Решить систему векторных уравнений можно, если число неизвестных составляющих (величин и направлений) векторов, входящих в систему, не превышает удвоенного количества уравнений. В данном случае система содержит четыре неизвестные составляющие: величину и направление вектора VA
'
, величину вектора VA
'
A
и величину вектора VA
'
B
. Следовательно, система решается.
Для решения системы необходимо в масштабе, используя правило сложения векторов, построить эти уравнения из одной точки, в данном случае из полюса Р
. Вектор Ра
, изображающий скорость VA
, на плане уже есть; вектор скорости VA
'
A
необходимо с ним сложить, поэтому через конец вектора VA
(через точку а
на плане скоростей) проводим известное направление (линию, параллельную ВС
). Это все, что пока можно получить из первого уравнения системы.
Из второго уравнения: скорость VB
= 0, следовательно, этот вектор представляет из себя точку, совпадающую с полюсом Р
. Вектор VA
'
B
, направление которого известно, необходимо сложить с вектором VB
, для чего через конец вектора VB
, (т.е. полюс) проводим нужное направление (линию, перпендикулярную ВС
) до пересечения с уже проведенной через точку а линией.
Точка их пересечения и дает искомое решение системы уравнений, т.е. определяет конец вектора скорости VA
'
, поэтому на плане скоростей эта точка получает обозначение а'
.
Действительное значение скорости точки А'
равно:
VA
'
=
Pa
' *
μ
v
= 76мм * 0,015мс-1
/мм = 1.14м/с
Отрезок аа
на плане изображает скорость VA
'
A
, ее действительное значение также может быть определено произведением длины отрезка аа на масштабный коэффициент μ
v
VA
'
A
=
aa
' *
μv
= 64мм * 0,015мс-1
/мм = 0,96м/с
Скорость VA
'
A
направлена от точки а
к точке а'
на плане скоростей (проверьте по правилу сложения векторов первое уравнение решенной системы).
Далее определим угловую скорость звеньев 2 и 3 (ω2
=ω3
), так как вращательное движение для них общее (относительное движение – поступательное)
ω 2
= ω3
=
VA
'
B
/
LA
'
B
=
VA
'
/ АВ * μ
L
= 1.14мс-1
/ (147мм * 0,0038м/мм) = 2с-1
Вектор скорости точки А'
относительно точки В
равен вектору абсолютной скорости точки А'
, т.е. VA
'
B
=
VA
'
. Расстояние от точки А'
до точки В (
LA
'
B
)
может быть определено с помощью плана положений.
Направление угловой скорости ω 3
определяется следующим образом: мысленно перенесем вектор скорости VA
'
B
в соответствующую точку плана положений (точку А'
) и рассмотрим ее движение относительно точки В
; ясно, что вращение звена 3 осуществляется по часовой стрелке, что и показано круговой стрелкой на плане положений механизма в положении 1.
Затем в соответствии с предложенной выше последовательностью следует определить скорость точки С
, к которой присоединена следующая группа Ассура. Воспользуемся принципом подобия: так как точки В, А', С,
принадлежащие одному жесткому звену, расположены на плане положений на одной прямой, то и точки b
, (она же полюс Р
) а', с
тоже должны располагаться на одной прямой на плане скоростей. Из подобия фигур имеем
Pa
' /
BA
' =
Pc
/
BC
Следовательно
Pδ
= (
BC
*
Pa
') /
BA
' = (171мм * 76мм) / 72мм = 88мм.
Построим этот вектор на плане скоростей и определим
VC
=
PC
*
μV
= 1.29м/с
Теперь можно переходить к рассмотрению второй и последней в данном механизме группы Ассура, состоящей из звеньев 4 и 5 т.е. из шатуна BC и ползуна C
.
Необходимо определить скорость точки C
, принадлежащей вращательной кинематической паре, т.е. одновременно звену BC
и звену C
. Так как звено 5 совершает поступательное движение, а значит, скорости всех точек этого звена равны и направлены в одну сторону – вдоль направляющей, то известно направление скорости точки C
. Скорость точки B
определена выше по правилу подобия. Составим векторное уравнение, связывающее скорость точек B
и C
:
→ → → →
VC
=
VB
+
VCB
(
VCB
┴
CB
),
VC
||
направляющей,
где VDC
– вектор скорости в относительном вращательном движении точки C
относительно точки B
, следовательно, направление этого вектора перпендикулярно положению звена BC
на плане положений.
Так как полученное уравнение содержит всего две неизвестные составляющие – величины векторов VC
и VCB
, то оно может быть решено. Для этого через точку b
на плане скоростей проведем линию, перпендикулярную положению звена CD
на плане положений, а через полюс – линию, параллельную направляющей (вертикальную линию). Точка их пересечения есть точка c
– конец вектора Pc
, изображающего на плане скорость точки C
. Тогда
VB
=
PB
*
μV
= 0,35м/с
Отрезок dc
на плане скоростей изображает скорость VDC
, которая направлена на плане в сторону точки d.
Угловая скорость звена CD
(ω4
)
может быть определена
ω 4
=
VBC
/
LCB
= (
cb
*
μ
V
) /
LCB
= 6.6с-1
.
Для определения направления угловой скорости звена BC
следует мысленно поместить вектор относительной скорости VCB
в соответствующую точку плана положений, т.е. в точку C
. Очевидно, что под действием этого вектора звено вращается по часовой стрелке.
Таким образом, строятся планы скоростей для всех положений механизма, приведенных на плане положений. Все планы можно строить из одного приведенного на плане положений. Все планы можно строить из одного полюса. Результаты расчетов сводят в таблицу, при этом в пояснительной записке не следует повторять формулы и расчеты для всех положений механизма.
Значения скоростей точек и угловых скоростей звеньев механизма.
| Положение
механизма
Кинематич.
параметры
|
0(6)
|
1
|
2
|
3
|
k
|
4
|
5
|
| VA
|
0
|
9,8
|
|
|
|
|
|
| VA
'
|
0
|
1.14
|
1.6
|
0.9
|
0
|
0.6
|
1.4
|
| VB
|
0
|
1.32
|
1.59
|
1.08
|
0
|
0.98
|
3.08
|
| VC
|
0
|
1.29
|
1.60
|
1.05
|
0
|
0.95
|
3.60
|
| ω3
|
0
|
2.0
|
2.6
|
1.8
|
0
|
1.5
|
3.68
|
| ω4
|
0
|
6.60
|
0.16
|
0.42
|
0
|
0.44
|
0.37
|
| VS3
|
0
|
0.65
|
0.80
|
0.53
|
0
|
0.48
|
1.80
|
| VS4
|
0
|
1.30
|
1.59
|
1.05
|
0
|
0.29
|
3.75
|
Определение ускорений точек и угловых ускорений звеньев
Решение этой задачи также проводится графоаналитическим методом, т.е. построением плана ускорений. В соответствии с заданием план ускорений строится только для одного положения – того, для которого будет проводиться силовой анализ (на рабочем ходу для наиболее нагруженного положения механизма).
Построение плана ускорений проводится в той же последовательности, что и плана скоростей. Свойства плана ускорений аналогичны свойствам плана скоростей, поэтому отдельно не описываются.
Построение плана ускорений проводим для первого положения механизма, так как
это наиболее нагруженное положение (сила полезного сопротивления максимальна).
Ускорение точки А
, совершающей вращательное движение вокруг точки О
, складывается из двух составляющих:
→ → →
аА
= аА
n
+
aA
τ
где аА
n
-
вектор нормальной составляющей ускорения точки А
, направленный к центру вращения и равный по модулю
аА
n
=
ω
1
2
*
LOA
= 9.82
с-2
* 0,15м = 14.4м/с-2
аА
τ
– вектор тангенциальной составляющей ускорения точки А
, направленный перпендикулярно вектору нормальной составляющей и равный по модулю
аτ
А
= ε1
*
LOA
= 0
поскольку в данном случае угловая скорость кривошипа задана постоянной, а значит угловое ускорение кривошипа ε1
= 0
.
Следовательно, ускорение точки А
конца кривошипа будет равно нормальной состаляющей аА
n
, и мы можем построить этот вектор. Для этого выберем полюс плана ускорений, обозначим его буквой π
, построим вектор, параллельный соответствующему положению кривошипа длиной, например, 75мм. Определим масштабный коэффициент
μ а
= а
n
A
/
πa
= 14.4мс-2
/ 100мм = 0,14м*с-2
/ мм
Соблюдая последовательность, принятую при построении плана скоростей, определяем ускорение точки А'
, для чего составляем и решаем систему векторных уравнений.
На основании теоремы сложения ускорений (вектор абсолютного ускорения точки равен сумме векторов ускорений в переносном движении, относительном и ускорения Кориолиса) можем записать:
→ → → →
аА'
= аА
+ аА'А
k
+
aA
'
A
o
(1)
→ → → →
aA
'
=
aB
+
aA
'
B
n
+
aA
'
B
τ
(2)
где аА
– вектор ускорения точки А
кривошипа и кулисного камня (величина и направление его известны);
аА'А
о
– вектор относительного ускорения точки А'
кулисы относительно точки А
(у него известно только направление – вдоль кулисы ОВ
);
аА'А
k
– вектор ускорения Кориолиса, по модулю равный
аА'А
k
= 2
ω
3
*
VA
'
A
= 2 * 2,3
c
-1
* 0,96м*с-1
= 4,14м/с2
Кориолисово ускорение возникает в том случае, когда вектор относительной скорости поворачивается (т.е. переносное движение – вращательное), поэтому его еще называют поворотным
ускорением. Направление его определяется поворотом вектора относительной скорости VA
'
A
на 90о
в направлении переносной угловой скорости ω3
.
аВ
– вектор ускорения точки В
(переносное ускорение, равное нулю, так как точка В
принадлежит еще и стойке);
аА'В
n
– нормальная составляющая вектора относительного ускорения точки А'
относительно точки В
, равная по модулю
аА'В
n
= ω3
2
*
LA
'
B
=0,16м/с-2
направленная к центру вращения, т.е. от точки А'
к точке О1
;
аА'В
τ
– тангенциальная составляющая вектора относительного ускорения точки А'
относительно точки В, для которого известно только направление, перпендикулярное нормальной составляющей (или кулисе ВС
).
Отметим, что в уравнении (2) Кориолисова ускорения нет, так как в этом случае переносное вращательное движение отсутствует.
Поскольку полученная система двух уравнений содержит четыре неизвестные составляющие векторов, то она может быть решена.
Решаем графически систему уравнений:
-
из точки а
плана ускорений проводим в соответствующем направлении вектор ak
, изображающий ускорение Кориолиса, в принятом масштабе
ak
=
aA
'
A
k
/
μa
= 29,6мм;
- через точку k
проводим направление вектора аА'А
о
;
- из полюса π
проводим в соответствующем направлении вектора π
n
1
,
изображающий нормальную составляющую аА'В
n
в принятом масштабе
π
n
1
=
aA
'
B
n
/
μa
= 0,16м*с-2
/ 0,012м*с-2
= 13мм.
Этот вектор проводим из полюса потому, что ускорение точки В
равно нулю, и следовательно, точка b
совпадает с полюсом;
- через точку n
1
проводим направление вектора аА'В
τ
до пересечения с направлением вектора аА'А
о
, проведенный ранее через точку k
.
Точка пересечения и будет точкой а'
, соединив которую с полюсом, получим величину и направление ускорения точки А'
.
Модуль ускорения точки А'
будет равен
аА'
= πа' * μа
= 29мм * 0,012м*с-2
/мм = 0,34м*с-2
,
а направление соответствует направлению вектора πа'
на плане ускорений.
Угловое ускорение третьего звена ε3
и равное ему ε2
можно определить с помощью найденной в результате решения уравнений тангенциальной составляющей ускорения вращательного движения:
ε3
=
aA
'
B
τ
/
LA
'
B
=(
n
1
a
'*
μa
)/(
A
'
B
*
μL
)=(25мм*0,012мс-2
/мм)/(72мм*0,005м/мм) = 0,83с-2
,
ибо вектор n
1
a
'
на плане ускорений изображает тангенциальную составляющую аА'В
τ
Направление углового ускорения определим, перенеся мысленно вектор n
1
a
'
с плана ускорений в точку А'
плана положений. Она не обозначена на плане, но мы помним, что она совпадает в данном случае с точкой А
. Направление углового ускорения на плане положений показано круговой стрелкой.
Ускорение точки С
найдем по принципу подобия в плане ускорений
πа' / πс = ВА' / ВС,
отсюда πс = (ВС*πа') / ВА' = (100мм*29мм) / 72мм = 40мм
Построим этот вектор на плане ускорений как продолжение вектора πа'
и найдем величину ускорения точки С
:
аС
= πс * μа
= 40мм * 0,012м*с-2
/мм = 0,48м*с-2
Определим далее ускорение точки D, для чего составим уравнение
→ → → →
aD
=
aC
+
aDC
n
+
aDC
τ
где аС
– в данном случае переносное ускорение, у которого известны величина и направление;
а
DC
n
– вектор нормальной составляющей относительного (вращательного) ускорения точки D
относительно точки С
, по модулю равный
aDC
n
=
ω
4
2
*
LDC
= 0,412
с-2
* 0,2м = 0,034м/с-2
и направленный вдоль звена DC
к точке С
;
а
DC
τ
– вектор тангенциальной составляющей того же ускорения, у которого известно только направление – перпендикулярно звену DC
.
Кроме того, нам известно направление ускорения точки D
(звено 5 движется поступательно), следовательно, уравнение содержит две неизвестные составляющие входящих в него векторов, и его можно решить графически на плане ускорений следующим образом:
- из точки b
в соответствующем направлении проведем вектор с
n
2
, изображающий составляющую а
DC
n
, в масштабе
cn
2
=
aCB
n
/
μa
= 0,034м*с-2
/ 0,012м*с-2
/мм = 3мм
;
через точку n
2
проведем направление вектора а
DC
τ
(линию, перпендикулярную DC
) до пересечения с направлением ускорения а
D
, т.е. с вертикальной линией, проведенной через полюс. Точка пересечения и есть точка d
плана ускорений, следовательно,
а
D
=
πd
*
μa
= 25мм * 0,012м*с-2
/мм = 0,3м*с-2
.
Угловое ускорение звена DC определяется
ε4
=
aDC
τ
/
LDC
=
n
2
d
*
μa
/
DC
*μ
L
=(17мм*0,012мс-2
/мм)/(40мм*0,005м/мм)=4,5с-2
Направление углового ускорения звена DC
определим с помощью вектора n
2
d
, изображающего тангенциальное ускорение а
DC
τ
. Мысленно перенося этот вектор в точку D
плана положений, покажем направление углового ускорения круговой стрелкой.
Силовой анализ механизма
Целью силового анализа является определение реакций в кинематических парах
, т.е. тех сил, которые передаются в кинематической цепи от одного звена к другому. При решении этой задачи методом кинетостатики (или методом Н.Г. Бруевича) появляется возможность определить и уравновешивающую силу
– силу, которую должен сообщить двигатель для нормального функционирования механизма технологической машины, или ту силу полезного сопротивления, которую может преодолеть двигатель.
Метод кинетостатики основан на применении принципа Даламбера
, который формулируется следующим образом: если в любой момент времени к каждой из точек системы, кроме действующих на нее внешних сил приложить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.
Это позволяет вести расчет неравномерно движущихся звеньев по уравнениям статики.
В общем случае, когда звено совершает плоское движение, силы инерции приводятся к главному вектору сил инерции
F
И
,
приложенному к центру масс звена и главному моменту пар сил инерции МИ
, определяемый по соотношениям:
→
F
И
= -m * aS
→
M
И
= -JS
* ε
где m – масса звена, кг;
aS
– ускорение центра масс звена, м/с2
JS
– осевой момент инерции звена относительно центра масс, кг*м2
ε – угловое ускорение звена, с2
Отметим, что реакция в кинематической паре 5-го класса всегда содержит две неизвестные составляющие (в поступательной – точку приложения и величину силы, во вращательной – величину и направление силы), и механизм без избыточных связей является статически определимым. Для упрощения расчетов значительно удобнее разложить его на группы Ассура, которые также являются статически определимым (доказательства этого утверждения см. в (3) или (4)).
Таким образом, силовой анализ механизма следует проводить по структурным группам, начиная с группы, наиболее удаленной от механизма I класса, и заканчивая сомим механизмом I класса.
Иными словами, силовой анализ механизма проводится в порядке, обратном кинематическому.
Рассмотрим проведение силового анализа для первого положения механизма, структурный и кинематический анализ которого приведены в работе (1). Решение этой задачи выполним графоаналитическим методом.
Для проведения силового анализа необходимо знать все внешние силы, в том числе силы инерции, действующие на механизм, поэтому необходимо задаться массами и моментами инерциизвеньев, а также координатами центров масс звеньев.
Массы звеньев, совершающих вращательное и плоскопараллельное движение, определяются по эмпирической формуле:
mi
=
q
*
li
где mi
– масса i-го звена, кг;
q
– массовый коэффициент, принимаемый 15кг/м.
li
– длина i-го звена,м.
Массы звеньев округляются до целых величин кратных 5.
Массы звеньев, совершающих поступательное движение, принимают равными: для строгальных, долбежных станков, пуансонов, прессов – 80…150кг, для камней кулисных механизмов – массе кривошипов.
Моменты инерции стержневых звеньев механизма принимать расчетом по формуле:
Ji
= (
mi
*
li
2
) / 10,
где Ji
– момент инерции массы i-го звена, кг*м2
;
mi
– масса i-го звена, кг;
li
– длина i-го звена,м.
Где J- момент инерции массы i-го звена, кг·м2
;
mi
- масса i-го звена, кг;
li
- длина i-го звена, м.
Моменты инерции массы округлить до двух значащих цифр кратных 5.
Центры тяжести звеньев расположены посередине звеньев, если в заданиях нет дополнительных указаний относительно их расположения. Центры масс треугольных звеньев лежат в точке пересечения медиан треугольника.
Максимальная величина силы полезного сопротивления принимается в 5…10 раз больше, чем сумма сил тяжести всех звеньев механизма.
n
Fп.с.
= 5…10·∑Gi
i
=1
где Gi
– сила тяжести i-го звена, Н.
Для простоты укажем только значения выбранных инерционных параметров:
m1,
m2,
m3,
m4,
m5,
JS
4,
JS
5
Моменты инерции остальных звеньев будем считать пренебрежимо малыми.
Выделим последнюю группу Ассура, состоящую из звеньев 4 и 5. Вычертим в масштабе μL
= 0,0038 м/мм план группы в соответствующем положении и определим все силы, действующие на звенья этой группы.
Сила полезного сопротивления определяется заданием, в данном случае приложена в точке D, направлена вверх. Величина определена по диаграмме Fп.с.
= f(SD
), которая вычерчивается в пределах величины хода 5-го звена; масштабный коэффициент силы Fп.с.
на диаграмме выбираем произвольно, с учетом свободного места рядом с планом положений.
Силы тяжести приложены в центрах масс звеньев (S4
иD), направлены вертикально вниз, по величине равны:
G4
=294 Н
G5
= 980 Н
Где g – ускорение свободного падения, g =9,8 м/с2
.
Силы инерции приложены также в центрах масс звеньев, направлены противоположно направлению ускорений центров масс и равны:
FИ4
= m4
·aS
4
= 30*6,58=197,4 Н
FИ5
= m5
·aD
=100*6,44=644 Н
Кроме того, на звено 4 будет действовать момент пар сил инерции:
МИ4
= JS
4
·ε4
=7,5*4,5= 33,75 Нм
направленный против углового ускорения звена 4, т.е. по часовой стрелке.
Любая сила (вектор) характеризуется величиной, направлением и точкой приложения ( центр шарнира), в поступательных известно направление ( перпендикуляр к оси движения).
Реакция F34
в кинематической паре С (воздействие отсоединенного третьего звена на четвертое) – известна точка приложения – центр шарнира, т.е. точка С, но неизвестны величина и направление силы. Для удобства расчета разложим неизвестную реакцию F34
на две составляющие: F34
n
, действующую вдоль звена CD, и F34
τ
, ей перпендикулярную. Направление векторов этих реакций – произвольное.
Реакция F05
в кинематической паре (реакция отсоединенной стойки 0 на ползун 5) – неизвестны величина силы, направленной перпендикулярно направляющей и приложенной в центре ползуна, и величина момента пар сил. Для удобства расчета силу и момент заменим одной силой F05
, смещенной от оси ползуна на неизвестное расстояние х.
Реакция F45
(или F54
) в кинематической паре в внутренняя для данной группы асура реакция между звеньями 5 и 4 (между шатуном и ползуном) также содержит две неизвестные составляющие: величину и направление, которые необходимо найти в результате силового анализа. На плане группы эти реакции не показаны, так как они являются внутренними силами, следовательно, взаимно уравновешены.
Под действием всех вышеперечисленных сил группа Асура (и любое из ее звеньев) находятся в равновесии, т.е. интересующие нас неизвестные составляющие реакции в кинематических парах могут быть определены из уравнений статики.
Ориентируясь на применение метода плана сил, который позволяет найти не более двух неизвестных составляющих из одного векторного уравнения статики, рекомендуется следующий порядок силового анализа данной группы.
Величину составляющей Fτ
34
найдем из условия равновесия звена 4:
∑
n
i
=1
MD
(
Fi
) =0
где MD
(
Fi
)
– момент i-ой силы относительно точки D
Для нашего примера
Fτ
34
*
lCD
+
M
и4
+
F
и4
*
h
1
*
μL
–
G
4
*
h
2
*
μL
= 0.
где h
1
и h
2
– плечи сил F
и4
и G
4
, соответственно, относительно точки D
, определяемые непосредственно на плане группы в мм.
Из полученного уравнения можно определить величину Fτ
34
:
Fτ
34
= (
G
4
*
h
2
*
μL
–
Fμ
4
*
h
1
*
μL
–
M
и4
) /
lCD
=
= (294 * 14 * 0,0038 – 197,4 * 33 * 0,0038 – 33,75) / 1,71 = 25,08Н.
Для построения плана сил составим векторное уравнение равновесия группы Ассура (сумма всех сил, действующих на группу, равна нулю), при этом соблюдая условие, впоследствии облегчающие решение нашей задачи:
- неизвестные составляющие (в нашем случае Fn
34
и F
05
), будем располагать по краям уравнений;
- в уравнение сначала включим все силы, принадлежащие одному звену, затем все силы, принадлежащие другому;
- составляющие одной и той же силы, например Fτ
34
и Fn
34
, не будем отрывать друг от друга.
Таким образом,
→ → → → → → → →
F
05
+
Fn
.
c
.
+
G
5
+
F
И5
+
F
И4
+
G
4
+
Fτ
34
+
Fn
34
=0.
Построение плана сил группы CD – в и есть решение этого уравнения. Последовательность решения (см. рис.: план сил группы CD – D):
- выберем масштабный коэффициент μF
равный 16Н/мм;
- проведем известное направление силы F05
– горизонтальную линию;
- выберем на ней произвольную точку и из нее отложим вектор Fn
.
c
.
в принятом масштабе (при μF
=85,3 Н/мм, Fn
.
c
.
=12794/85,3 = 150мм) и в соответствующем направлении (в нашем примере – вверх);
- из конца вектора Fn
.
c
.
отложим в соответствии с направлением действия вектор силы G5
в том же масштабе, т.е. G5
=980/85,3 = 11,5мм (на построенном плане для наглядности вектор G5
сдвинут вправо);
- далее в последовательности, соответствующей порядку суммирования векторов в решаемом уравнении, в том же масштабе и соответствующих направлениях откладываем все известные векторы, т.е. FИ
, FИ4
, G4
, Fτ
34
(в данном случае векторы FИ5
, FИ4
, изображаются точкой ввиду их малости);
- из конца вектора Fτ
34
проведем направление вектора Fn
34
до пересечения с проведенным в начале решения направлением вектора F05
.
Равенство нулю суммы сил на плане сил равнозначно замкнутости многоугольника сил, следовательно, из полученного решения можно определить величины и направление действия искомых сил: F05
=
и направлена влево, как это было предварительно принято при составлении расчетной схемы группы CD-D.
Вектор силы F34
имеет смысл определить полностью, а не по составляющим. Для этого сложим составляющие прямо на плане, т.е. соединим начало вектора Fτ
34
и конец Fn
34
. Итак реакция F34
= 65,75 Н
С помощью этого же плана может быть определена и реакция в шарнире D. Действительно, из равновесия звена 5 можем записать (сумма всех сил, действующих на звено 5, равна нулю):
→ → → → → → →
F
05
+
Fn
.
c
.
+
G
5
+
F
И5
+
F
И
+
G
4
+
F
45
=0.
План сил звена 5 можно построить отдельно, а можно выделить силы, действующие на 5-е звено на плане сил группы звеньев 4-5.
Все эти векторы (кроме F45
) уже просуммированы на построенном плане сил, следовательно, вектор F45
будет их замыкающим вектором: соединим конец вектора FИ
, а так как он представлен точкой, то конец вектора G5
, с началом вектора F05
.
Это и будет F45
=
Оставшуюся неизвестную (координату х точки приложения силы F05
)
можно определить из другого уравнения равновесия звена 5. Если взять сумму моментов сил, которая могла бы составить момент – сила F05
, следовательно,
F05
· х = 0,
А так как F05
не равна нулю, то х=0.
Это значит, что реакция F
05
также проходит через точку D
.
Далее рассмотрим силовой анализ следующей группы Ассура, состоящей из звеньев
3 и 2
. Вычертим план группы в соответствующем положении механизма (см. рис.: группа Ассура II класса 3-го вида). Прикладываем все внешние силы, действующие на звенья группы (для лучшего представления внутренней реакции (F
32
=-
F
23
) на построенной расчетной схеме группа разделена на два звена).
Реакция со стороны ранее анализированной группы
F
43
действует на звено 3 механизма (кулису) в точке С
. Величина и направление ее были определены при анализе предыдущей группы: реакция F
43
равна по величине и противоположна по направления реакции F
34
.
Сила тяжести
приложена в центрах масс звеньев (в точках S
3
и A
), направлены вертикально вниз и равны:
G
3
=
m
3
*
g
= 30 * 9,8 = 294
H
,
G
2
=
m
2
*
g
= 10 * 9,8 = 98
H
.
Силы инерции
приложены также в центрах масс звеньев, направлены противоположно направлениям ускорений центров масс (см. план ускорений) и равны:
F
И
3
= m3
* aS3
= m3
* πs3
* μa
= 30 * 26 * 0,14 = 109,2 H,
F
И2
=
m
2
*
aA
= 10 * 0,9 = 4,5
H
.
Кроме того, на звено 3 будет действовать момент пар сил инерции:
M
И3
=
JS
3
*
ε
3
= 7,5 * 9,3 = 69,75 Н*м
,
направленный против углового ускорения звена 3 (против часовой стрелки).
Реакции в кинематических парах
и являются целью анализа, т.е. в каждой реакции необходимо определить по две неизвестные составляющие.
Реакция F
03
в кинематической паре В
(реакция отсоединенной стойки 0 на кулисе 3) неизвестна по величине и направлению, но известна точка приложения – центр шарнира В
. В данном случае раскладывать ее на две составляющие нецелесообразно, поэтому просто покажем эту реакцию пунктиром на плане групп.
Реакция F
23
в кинематической паре А'
(реакция со стороны кулисного камня 2, на кулису 3) известна по направлению – перпендикулярно направляющей, но известны ее величина и точка приложения (как для любой поступательной пары 5-го класса).
Реакция F
32
действует на второе звено, равна по величине и противоположна по направлению реакции F
23
.
Реакция F
12
в кинематической паре А
(отсоединенного кривошипа 1, на звено 2) неизвестна по величине и направлению; известна точка приложения – центр шарнира А
(на плане положений группы также показана пунктиром).
Наиболее просто поставленная задача может быть решена следующим образом:
Из равновесия звена 2 (камня кулисы) можно определить точку приложения реакции F
32
: так как сумма моментов всех сил относительно точки А
должна быть равна нулю, то, следовательно, реакция F
32
проходит через точку А
, как и все остальные силы, действующие на звено 2. На третьем звене, следовательно, точкой приложения реакции F
23
будет точка А'
.
Из условий равновесия звена 3 составим уравнение моментов всех сил относительно точки В:
F
23
*
lBA
'
+
G
3
*
h
3
*
μL
–
M
И3
–
F
И3
*
h
4
*μ
L
–
F
43
*
h
5
* μ
L
= 0,
где hi
– плечи соответствующих сил, измеряемых на плане группы.
Из приведенного уравнения можно найти величину реакции F
23
как единственную неизвестную величину:
F
23
= (
M
И3
+
F
И3
*
h
4
* μ
L
+
F
43
*
h
5
* μ
L
–
G
3
*
h
3
* μ
L
) /
lBA
'
F
23
= (69,75 + 93,2 * 65 * 0,0038 + 167 * 159 * 0,0038 – 294 *85 * 0,0038) / 151* 0,0038 = 15020 Н
Величина реакции получилась положительной, следовательно, на плане положений направление силы было выбрано верно.
Далее составим и решим векторное уравнение равновесия звена 3 (неизвестную реакцию в уравнении запишем последней):
→ → → → →
F
43
+
F
23
+
F
И3
+
G
3
+
F
03
= 0.
Выбрав масштабный коэффициент (для данного плана также μ
F
= 16 Н/мм
) на плане сил звена 3 суммируем силы, откладывая их по порядку, начиная с F
43
и замыкая многоугольник вектором F
03
. Измерив полученный вектор на плане и умножив его на масштабный коэффициент, получим:
F
03
= 84 мм * 85,3 Н/мм = 7165,2 Н
.
Аналогично построим план сил звена 2:
→ → → →
G
2
+
F
И2
+
F
32
+
F
12
= 0
По правилу сложения векторов в масштабе (μ
F
= 85,3 Н/мм
) откладываем векторы сил, входящих в уравнение. Замыкающим вектором будет искомая F
12
, величина которой определяется также произведением длины соответствующего вектора на плане сил на масштабный коэффициент:
F
12
= 176мм * 85,3Н/мм = 15012,8Н
Осталось провести силовой анализ начального механизма – механизма 1-го класса. Будем считать, что механизм приводится в движение от двигателя через зубчатую передачу, последнее зубчатое колесо которой с числом зубьев Z
2
= 30
находится на одном валу с кривошипом ОА
. В зацеплении с ним находится колесо с числом зубьев Z
1
= 20
, модуль передачи m
= 6мм
. Вычертим план механизма 1 класса в соответствующем положении совместно с указанной парой зубчатых колес (см. рис.: механизм 1 класса). Для этого необходимо определить диаметры делительных окружностей колес:
D
2
=
m
*
Z
2
= 6мм * 19 * 10-3
м/мм = 0,114м;
D
1
=
m
*
Z
1
= 6мм * 20 * 10-3
м/мм = 0,08м
.
Диаметры делительных окружностей вычерчиваем в принятом ранее масштабе μ
L
=
=0,0038 м/мм.
Определим силы, действующие на кривошип ОА и соединенное с ним зубчатое колесо.
Реакция со стороны присоединяемой группы Ассура
F
21
(давление звена 2 на звено 1) определена при анализе предыдущей группы Ассура, равна реакции F
12
и направлена противоположно ей.
Сила тяжести приложена в точке О
(считаем кривошип уравновешенным звеном), направлена вертикально вниз и равна:
G
1
=
m
1
*
g
= 10 * 9,8 = 98
H
Реакция
F
01
(внутренняя реакция действия стойки О на кривошип 1) – неизвестна по величине и направлению (на плане показана пунктирной линией).
Уравновешивающая сила Fy
– cила, сообщаемая двигателем и приводящая в движение механизм. В данном случае она может рассматриваться как реакция в зацеплении зубчатых колес. Поскольку это высшая пара, то для нее известны и точка приложения – полюс зацепления (на плане точка «к»
) и направление – линия зацепления. Для стандартных нулевых колес линия зацепления образует угол 20о
с перпендикуляром к межосевому расстоянию (3,4). Так как для пары колес в зависимости от их направления вращения и передачи мощности возможны две линии зацепления, воспользуемся следующим правилом для нахождения действующей линии зацепления у колес с внешним зацеплением: повернем вектор скорости точки «к»
(в данном случае направленной вверх) на угол зацепления α
W
в сторону вращения ведомого колеса. Ведомым колесом в нашем случае является колесо 2, соединенное с кривошипом, т.к. сила F
21
создаем момент, направленный против вращения колеса и является силой сопротивления. Меньшее колесо является ведущим, а сила Fy
является движущей силой. Она создает крутящий момент, действующий в направлении угловой скорости ω1
.
Величину уравновешивающей силы можем определить из уравнения моментов всех сил относительно точки О.
Fy
·hy
- F
21
·h =0,
Откуда
Fy
= (
F
21
·h)/ hy
Отметим, что силы инерции для данного механизма не учитываются, так как центр масс кривошипа находится в неподвижной точке, а угловое ускорение равно нулю.
Оставшуюся неизвестную реакцию F
01
определим на плане сил, для чего составим векторное уравнение кривошипа:
→ → → →
F
21
+
F
у
+
G
1
+
F
01
= 0.
Величина и направление F
01
определяется также с помощью плана сил. Складываем первые три силы с учетом масштабного коэффициента; замыкая силовой многоугольник, получаем изображение реакции F
01
.
Измерив величину данного вектора на плане и умножив ее на масштабный коэффициент, получим:
F
01
=141*26,89= 37631,49
Проверить правильность выполненных расчетов следует, определив с помощью метода Н.Е. Жуковского значение уравновешивающей силы F и сравнив полученные результаты.
Определение Уравновешивающей силы по методу Н.Е. Жуковского
Теорема Н.Е. Жуковского основана на принципе возможных перемещений: «для равновесия механической системы необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю».
Сформулируем теорему Жуковского: если все внешние силы, действующие на механизм в рассматриваемый момент времени, в том числе силы инерции, перенести параллельно самим себе в соответствующие точки повернутого на 90° плана скоростей, то такой план скоростей можно рассматривать как жесткий рычаг с опорой в полюсе плана, находящийся под действием всех рассматриваемых сил в равновесии.
Действующие на звенья моменты следует заменить парами сил.
Метод Жуковского может быть применен для нахождения любой одной неизвестной силы, если точка приложения и линия действия этой силы неизвестны.
Воспользуемся данным методом для проверки правильности выполненного силового анализа механизма. Определим уравновешивающую силу, считая ее неизвестной по величине и в случае, если величина Fy
, найденная по методу Жуковского, совпадает или будет отличаться в пределах 5% от величины, найденной кинетостатическим методом, будем считать силовой расчет выполненным верно.
На свободном поле листа графических расчетов вычертим повернутый на 90° план скоростей механизма для того же первого положения. Здесь же на плане поместим и вектор скорости точки «к» – токи приложения уравновешивающей силы. Для определения точки «к» на плане скоростей можно воспользоваться принципом подобия в плане скоростей.
На полученный жесткий рычаг действуют силы:
- в точке «к» - уравновешивающая сила Fy
;
- в точке «а» - силы тяжести G
2
и инерции F
И2
;
- в точке «S3
» - силы тяжести G
3
и инерции F
И3
;
- в точке «S4
» - силы тяжести G
4
и инерции F
И4
;
- в точке «d» - силы полезного сопротивления Fп.с.
, тяжести G
5
и инерции F
И5.
-
в токе «с» - силы F
М3
и F
М4,
полученные в результате замены моментов инерции МИ3
и МИ4
парами сил F
М3
= МИ3
/ lBC
,
F
М4
= МИ4
/ lCD
,
Вторые составляющие пар сил приложены соответственно в точка «b» и «d» ;
Запишем уравнение равновесия рычага Жуковского под действием всех приложенных сил:
Fy
·hy
+
G
2
·
h
1
+
G
3
·
h
2
-
F
М3
·pc+ F
М4
·
h
4
-
F
И4
·
h
5
+
G
4
·
h
6
-
F
М4
·
h
1
–
pd
(
Fn
.
c
.
+
F
И5
–
G
3
)=0,
где hy
–
плечо уравновешивающей силы;
h
1
–
плечи соответствующих сил относительно полюса, измеренные непосредственно на рычаге Жуковского.
Отсюда определим уравновешивающую силу:
Fy
=
G
2
·
h
1
+
G
3
·
h
2
-
F
М3
·pc+ F
М4
·
h
4
-
F
И4
·
h
5
+
G
4
·
h
6
-
F
М4
·
h
1
–
pd
(
Fn
.
c
.
+
F
И5
–
G
3
)/
hy
=0,
Fy
=25697,2; δ=3,71%
Расчет и построение диаграммы приведенного момента сил полезного сопротивления
Определение закона движения механизма, состоящего из n подвижных звеньев, осуществляется путем решения основного уравнения движения, связывающего работу внешних сил с изменением кинетической энергии
∑(Ad-Ac)=∆T (3)
где Ад
, Ас
– соответственно работа движущих сил и сил сопротивления, дж;
ΔТ – изменение кинетической энергии за тот же промежуток времени, дж.
Для упрощения записи основного уравнения движения используется прием, называемый приведением сил и масс. Это позволяет заменить сложный, многозвенный механизм моделью, представляющей собой механизм I класса, к которому приложена одна сила (или момент пары сил), эквивалентная по своему действию всем силам, действующим на звенья реального механизма, и который характеризуется одной массой (или осевым моментом инерции), эквивалентной массам и осевым моментам инерции всех звеньев реального механизма.
Такая замена реального механизма одномассовой моделью возможна при соблюдении двух условий:
1) – мощность приведенной силы (приведенного момента пары сил) должна быть равна сумме мощностей всех внешних сил, действующих на звенья механизма;
2) – кинетическая энергия звена приведения должна быть равна сумме кинетических энергий всех звеньев реального механизма.
В качестве звена приведения обычно выбирают кривошип (начальное звено), поскольку задача динамического расчета состоит в том, чтобы определить истинную скорость кривошипа в течение цикла движения, т.е. определить закон движения начального звена.
Из первого условия определяют приведенный момент сил сопротивления, который для механизма. состоящего из n подвижных звеньев, совершающих поступательное, вращательное и плоскопараллельное движение, рассчитывается по формуле
Мпр
=∑(Fi
Vi
cosαi
+Mi
ωi
)/ωi
(4)
где Fi
,
Mi
– соответственно, сила и момент пары сил, приложенные к i – му звену;
Vi
– скорость точки приложения i- й силы;
αi
– угол между вектором силы Fi
и вектором скорости Vi
;
ωi
-угловая скорость i- го звена.
Из второго условия определяют приведенный осевой момент инерции, который для механизма, состоящего из n подвижных звеньев, совершающих поступательное, вращательное и плоскопараллельное движение, рассчитывается по формуле
Jпр
= ∑(mi
VSi
2
+JSi
ωi
2
)/ωi
2
(5)
где mi
, Ji
–соответственно, масса и осевой момент инерции I –го звена;
Vsi
– скорость центра масс I –го звена.
Для замены рассматриваемого механизма одномассовой моделью к начальному звену приводятся силы тяжести звеньев (Gi
) и силы полезного сопротивления (Fпс
). значения сил тяжести и полезного сопротивления, а также значения скоростей определены при выполнении первого листа курсового проекта; углы между направлениями векторов силы и скорости измеряются на плане скоростей, построенном на первом листе проекта. Для рассматриваемого нами механизма формула (4) примет вид:
Мпр
= (6) (6)
Представляя формулу (6) значения соответствующих скоростей, углов и силы полезного сопротивления для 1-го, 2-го, … 6-го положений механизма, получим значения приведенного момента сил сопротивления, значения которого свожу в таблицу
Приведенный момент сил
| Положение
механизма
|
0-6
|
1
|
2
|
3
|
4
|
5
|
| Величина Мпр
(Нм)
|
-1,7
|
-1500,6
|
-1496,7
|
-385,74
|
-145,33
|
-250
|
Знак «-» показывает, что приведенные моменты сил сопротивления направлены против скорости, поэтому диаграмма всегда располагается ниже оси абсцисс. Fпс
в положении холостого хода равна нулю, в нашем примере это 4 и 5 положения механизма.
По этим значениям в масштабе μм
= =21,43 строю диаграмму Мпр
=f(φ) за весь цикл установившегося движения, т.е. за один оборот кривошипа, тогда L2
= -83,18мм, L3
= - 46,8мм, L4
=-7,2мм, L5
=-18,5мм, L0
≈L6
≈0мм. =21,43 строю диаграмму Мпр
=f(φ) за весь цикл установившегося движения, т.е. за один оборот кривошипа, тогда L2
= -83,18мм, L3
= - 46,8мм, L4
=-7,2мм, L5
=-18,5мм, L0
≈L6
≈0мм.
Построение диаграммы работ сил сопротивления методом графического интегрирования
На оси абсцисс построенной диаграммы Мпр
=f(φ) участки движения 0-1, 1-2, … 5-6, соответствующие углу поворота кривошипа φ, делим пополам. Значения Мпр
, соответствующие серединам отрезков (на чертеже показаны пунктиром), сносим на ось ординат и полученные точки пересечения с осью ординат соединяю с точкой Р – полюсом интегрирования. Точка Р располагается на расстоянии Н=50мм от начала координат.
Углы наклона лучей, выходящих из точки Р, определяют изменение работы сил сопротивления на участках 0 -1; 1 - 2; ... 5 - 6. Поэтому в новой системе координат А
– φ1
,
расположенной ниже, проводим параллельно этим лучам отрезки в пределах соответствующих участков. Полученная ломаная линия представляет собой диаграмму работ сил сопротивления Ас
=f(φ1
). Масштабный коэффициент этой диаграммы рассчитывается по формуле
μА
=Н μм
μφ
,
Дж/мм (7)
где μм
, μφ
масштабные коэффициенты диаграммы Мпр
=
f
(
φ1
).
μφ
= рад/мм, тогда μА
=50∙21,43∙0,026=27,8 Дж/мм. рад/мм, тогда μА
=50∙21,43∙0,026=27,8 Дж/мм.
Согласно основному уравнению движения (3) при установившемся режиме за полный цикл движения Δ Т = 0,
то есть в начале и в конце цикла Ад
= Ас
.
Это означает, что ординаты диаграммы работ в положениях 0 и 6
равны и противоположны по знаку. Соединив начало координат с последней точкой диаграммы Ас
=
f
(φ1
),
которая соответствует значению работы Ас
в положении 6, получим угол наклона α, под которым должна располагаться диаграмма изменения работ движущих сил. Эта диаграмма располагается выше оси абсцисс, поскольку работа движущих сил - величина положительная. Поэтому под тем же углом α
проводим из начала координат прямую, в результате чего получаем диаграмму работ движущих сил А д
=
f
(φ1
).
Графически дифференцируя диаграмму Ад
=
f
(φ1
),
строим диаграмму момента движущих сил Мд
= f
(φ1
).
Для этого проводим из точки Р под углом α прямую до пересечения ее с осью ординат. Полученное значение определяет момент движущих сил, который является величиной постоянной, а значит диаграмма Мд
= f
(φ1
)
представляет собой прямую, параллельную оси абсцисс.( см. Приложение).
Как было отмечено ранее, работы сил сопротивления и движущих сил внутри цикла не равны между собой, поэтому ΔТ≠0. Чтобы построить диаграмму изменения кинетической энергии измеряют на диаграмме А – φ1
разность между значениями Ад
и Ас
. По этим значениям строят диаграмму ΔТ= f
(φ1
),
в том же масштабе что и предыдущую диаграмму.
Расчет и построение диаграммы изменения приведенного момента инерции
Для рассматриваемого механизма, формула (5) примет вид:
Jпр
= (8) (8)
Расчет по формуле (8) проводится для каждого из 6-ти положений. Соответствующие значения скоростей точек и угловых скоростей звеньев принимаю из таблицы скоростей, полученной в результате расчетов, выполненных на первом листе проекта. Значения Jпр
свожу в таблицу, а затем строю диаграмму Jпр
= f
(φ1
)
, в повернутой системе координат, с масштабным коэффициентом μJ
= Jпр
/ LJ
1
кг м2
/мм,
где LJ
1
– произвольно выбранный размер (40мм).
 Приведенный момент инерции Приведенный момент инерции
| Положение
механизма
|
0-6
|
1
|
2
|
3
|
4
|
5
|
| Величина Jпр
(кгм2
)
|
2,29
|
77,6
|
135,8
|
64,02
|
23,28
|
213,4
|
В соответствии с масштабным коэффициентом: LJ
2
=70мм, LJ
3
=33мм, LJ
4
=12мм, LJ
5
=110мм.
Построение диаграммы Виттенбауэра. Определение закона движения начального звена
Решение основной задачи динамики, т.е. определение истинной скорости начального звена производится с помощью кривой Виттенбауэра, которая строится путем исключения переменной φ1
из полученных ранее диаграмм ΔТ= f
(φ1
)
и Jпр
= f
(φ1
)
. Новое начало координат определяется пересечением осей абсцисс этих диаграмм. Проводятся новые координатные оси: вертикальная, на которой откладываю значения ΔТ, и горизонтальная, на которой откладываю значения Jпр
. Точки пересечения (0, 1,2, … и т. д.) соответствующих значений ΔТ и Jпр
соединяю последовательно плавной кривой, которая и называется диаграммой Виттенбауэра.
Из теоретического курса известно, что тангенс угла наклона секущей, проведенной из начала координат в любую точку кривой Виттенбауэра, пропорционален квадрату угловой скорости начального звена[4].
tgψ=ω1
μJ
/2μT
(9)
Отсюда можно определить скорость в любом положении механизма, при этом максимальное и минимальное значение угловой скорости соответствуют верхней и нижней касательным, проведенным к диаграмме Виттенбауэра под углами ψmax
и ψmin
(см. Приложение 3). Значения этих углов вычисляю согласно формулам:
tgψmax
=ω1
2
(1+δ) μJ
/2μT
tgψmin
=ω1
2
(1-δ) μJ
/2μT
,
Подставив числовые значения, получаю :
tgψmax
=9,82
(1+0,1)1,94/2∙26=3,9
tgψmin
=9,82
(1-0,1)1,94/2∙26=0,3
Определяю значения углов ψmax
=4,7°, ψmin
=3,7° и провожу касательные к диаграмме, которые отсекают на оси ординат отрезок АВ.
Тогда ωmax
=√ tgψmax
(2μT
/ μJ
)= 10м/с-1
ωmin
==√ tgψmin
(2μT
/ μJ
)=8.1м/с-1
Для определения значения скорости кривошипа во всех шести положениях, использую метод интерполяции, тогда:
 , отсюда , отсюда
ωi
= , ,
где АDi
– отрезки, полученные при пересечении касательных к точкам 1,2,…6, параллельных ψmax
и оси ординат.
Значения угловой скорости кривошипа в 6 положениях сведены в таблицу:
Истинные значения угловой скорости начального звена
| Положение
Механизма
|
0(6)
|
1
|
2
|
3
|
к
|
4
|
5
|
| Угловая
Скорость
ω, м/с-1
|
10
|
9,80
|
8,10
|
8,95
|
9,08
|
9,44
|
9,60
|
Определение момента инерции маховика
Поскольку отрезок АВ на диаграмме Виттенбауэра изображает в масштабе μТ
изменение кинетической энергии за цикл движения, то с учетом коэффициента неравномерности момент инерции маховика определяется по формуле[4]:
JM
=AB μТ
/δ ω1
2
(10)
АВ – значение отрезка на диаграмме, мм
JM
=64∙20/0,12∙7,72
=180,3
После определения момента инерции маховика рассчитывается средний диаметр обода D, на котором сосредоточена масса маховика
D= (11) (11)
где k1
,k2
– коэффициенты, принимаемые по конструктивным соображениям в размере 0,1 – 0,2. Эти коэффициенты показывают относительные размеры поперечного сечения обода маховика (аЧb) в долях от среднего диаметра а=k1
D ; b= k2
В
γ- удельный вес материала маховика (для стали принимают 78000Н/м3
).
отсюда
D=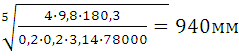
Размер маховика превышает допустимый (D<750 мм), то, по конструктивным соображениям маховик устанавливают на более быстроходный вал
JM
’
= JM
(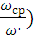 2 2
где ω,
- скорость вращения двигателя, ω,
= , n – частота вращения кривошипа. , n – частота вращения кривошипа.
тогда JM
’
=180,3(7,7∙30/3,14∙1430)2
= 0,47, подставляя это значение в (11), получаю, что D=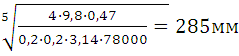 . .
а=0,2∙285=57мм,
b=0,2∙285=57мм.
Затем вычерчиваю эскиз маховика на листе
Список литературы
1. Методические указания по выполнению курсового проекта по ТММ (Раздел: Структурный и кинематический анализ). Екатеринбург: Изд-во Рос.гос.проф.-пед.ун-та, 2004. 38с.
2. Методические указания к выполнению курсового проекта по дисциплине «Теория механизмов и машин» (Раздел: Силовой анализ). Екатеринбург: Рос.гос.проф.-пед.ун-та, 2004. 24с.
3. Методические указания по выполнению курсового проекта по ТММ (Раздел: Динамика механизмов). Екатеринбург: ГОУ ВПО Рос.гос.проф.-пед.ун-та, 2007. 17с.
|