| 1. Основные принципы построения цифровых измерительных приборов. Определения
Цифровой измерительный прибор (ЦИП)
– средство измерений, автоматически вырабатывающее сигналы измерительной информации в цифровой форме. Цифровой измерительный прибор имеет ряд преимуществ перед аналоговыми приборами: удобство отсчитывания значений измеряемой величины, возможность полной автоматизации процесса измерений, регистрация результатов измерения с помощью цифропечатающих устройств и перфораторов. Поскольку результат измерения в ЦИП выражен в цифровом коде, измерительную информацию можно вводить в цифровую ЭВМ.
Не следует, однако, считать, что ЦИП в будущем полностью вытесняет аналоговые приборы. Аналоговые приборы просты и надежны. В тех случаях, когда оператору необходимо следить за уровнями изменяющихся во времени сигналов, стрелочные указатели более удобны из-за наглядности представления об изменениях величины, о ее минимальном значении, приближении к порогу и т. п.
В ЦИП происходит преобразование непрерывной измеряемой величины в цифровой код. Осуществляется этот процесс с помощью аналого-цифрового преобразователя (АЦП), в котором сигнал измерительной информации подвергается дискретизации, квантованию и кодированию.
Дискретизация, т. е. процесс преобразования непрерывного сигнала измерительной информации в дискретный, может осуществляться как по времени, так и по уровню. Дискретизация по времени выполняется путем взятия отсчетов сигнала X(t) в определенные детерминированные моменты времени. Таким образом, от сигнала измерительной информации сохраняется только совокупность отдельных значений. Промежуток времени Δt между двумя моментами дискретизации называют шагом дискретизации. Обычно моменты отсчетов на оси времени выбираются равномерно, т. е. шаг дискретизации Δt постоянен.
Дискретизация значений измерительного сигнала по уровню носит название квантования. Операция квантования сводится к тому, что непрерывная по времени и амплитуде величина заменяется ближайшим фиксированным значением по установленной шкале дискретных уровней. Эти дискретные (разрешенные) уровни образованы по определенному закону с помощью мер. Разность ΔХ между двумя разрешенными уровнями называют интервалом (шагом или ступенью) квантования. Интервал квантования может быть как постоянным, так и переменным. Временная дискретизация измерительного сигнала имеет смысл, когда его величина изменяется во времени. Если измерительный сигнал постоянен, достаточно осуществить квантование. Особым случаем является измерение времени (временного интервала).
Процесс дискретизации здесь теряет смысл, и осуществляется квантование самого времени.
Следующим преобразованием измерительного сигнала, является кодирование. Цифровым кодом называется последовательность цифр или сигналов, подчиняющаяся определенному закону, с помощью которой осуществляется условное представление численного значения величины. Графически описанные преобразования поясняются на рис.1. Исходный измерительный сигнал Х(t) (рис.1,а) представляет собой непрерывную функцию времени. Дискретизация  выполняется с интервалом Δt .Моменты дискретизации отмечены на рис.1,а цифрами 1, 2,... ..., 9. Практически такую дискретизацию можно осуществить путем амплитудной модуляции исходным сигналом Х(t) последовательности коротких импульсов с периодом Δt. Как видно из рис.1.б, значения сигнала Х(ti
), полученные после дискретизации, точно соответствуют мгновенным значениям функции Х(t). Если на том же рисунке отметить уровни квантования, расположенные друг от друга на расстоянии ΔХ, то часть дискретных значений сигнала окажется в промежутках между ними. Процесс квантования по уровню сводится к округлению дискретных значений сигнала до значений, соответствующих ближайшим разрешенным уровням. Так, в момент 1 мгновенное значение сигнала превышает уровень Х3
на величину, несколько меньшую ΔХ/2 (см. рис.1,б). Округление производится в сторону выполняется с интервалом Δt .Моменты дискретизации отмечены на рис.1,а цифрами 1, 2,... ..., 9. Практически такую дискретизацию можно осуществить путем амплитудной модуляции исходным сигналом Х(t) последовательности коротких импульсов с периодом Δt. Как видно из рис.1.б, значения сигнала Х(ti
), полученные после дискретизации, точно соответствуют мгновенным значениям функции Х(t). Если на том же рисунке отметить уровни квантования, расположенные друг от друга на расстоянии ΔХ, то часть дискретных значений сигнала окажется в промежутках между ними. Процесс квантования по уровню сводится к округлению дискретных значений сигнала до значений, соответствующих ближайшим разрешенным уровням. Так, в момент 1 мгновенное значение сигнала превышает уровень Х3
на величину, несколько меньшую ΔХ/2 (см. рис.1,б). Округление производится в сторону  уменьшения, и квантованное значение выбирается равным Х3
. В момент 2 значение сигнала превышает уровень X4
, на величину, большую чем ΔХ/2. Квантованное значение принимается равным Х5
(рис.1,в). Последний этап заключается в преобразовании квантованного сигнала X(ti
)кв
в цифровой код. На рис.1,г представлен для примера унитарный код X(ti
)код
, соответствующий значениям квантованного сигнала. При таком способе кодирования число импульсов в кодовой группе прямо пропорционально уровню квантованного сигнала. Например, отсчету 7 соответствует уровень квантования X6
, и в кодовой группе n7
, содержится шесть импульсов. уменьшения, и квантованное значение выбирается равным Х3
. В момент 2 значение сигнала превышает уровень X4
, на величину, большую чем ΔХ/2. Квантованное значение принимается равным Х5
(рис.1,в). Последний этап заключается в преобразовании квантованного сигнала X(ti
)кв
в цифровой код. На рис.1,г представлен для примера унитарный код X(ti
)код
, соответствующий значениям квантованного сигнала. При таком способе кодирования число импульсов в кодовой группе прямо пропорционально уровню квантованного сигнала. Например, отсчету 7 соответствует уровень квантования X6
, и в кодовой группе n7
, содержится шесть импульсов.
Из рис.1 ясно, что при дискретизации и квантовании сигнала возникает погрешность преобразования. Непрерывная функция X(t) анализируется только в моменты дискретизации. На интервале Δt между двумя отсчетными точками сигнал предполагается неизменным. Уменьшением интервала Δt, т. е. сближением отсчетных точек можно добиться снижения погрешности до допустимой величины. При измерении постоянных величин погрешность преобразования, связанная с дискретизацией, равна нулю. Погрешность, возникающая при квантовании непрерывной измеряемой величины, обусловлена конечным числом уровней квантования. Эта погрешность характерна для всех ЦИП, она носит название погрешности дискретности Δд
. При равномерном квантовании погрешность Δд
находится в пределах 0 Δд Δд
 ΔХ. ΔХ.
Следующий этап преобразований в ЦИП заключается в превращении цифрового кода в показания цифрового отсчетного устройства. Для этого необходим дешифратор, который превращает кодовые группы в соответствующие напряжения, управляющие работой цифрового индикатора.
Рассмотренная последовательность преобразований, осуществляемая в аналого-цифровом преобразователе (АЦП), дешифраторе и цифровом индикаторе, конечно, дает упрощенное представление о работе ЦИП. Примером может служить случай измерения постоянной величины. Для этого достаточно одного цикла преобразований, в результате которого получится кодовая группа. Но кодовая группа это «пакет» импульсов, передаваемый в течение короткого интервала времени. Результат измерений должен сохраняться на экране достаточно долго, например, до следующего цикла. Поэтому в состав ЦИП должно входить запоминающее устройство (ЗУ).
В заключение перечислим возможные режимы работы ЦИП и их характеристики.
Режим однократного измерения.
Этот режим удобен, когда измеряемый параметр постоянен. Команда на проведение измерения подается оператором, результат измерения хранится в запоминающем устройстве и воспроизводится на цифровом индикаторе. В ЦИП осуществляется квантование измерительного сигнала и его кодирование.
Режим периодического измерения.
Процесс измерения повторяется периодически через интервал Δt, установленный оператором. В ЦИП осуществляются операции дискретизации, квантования и кодирования. После каждого цикла измерения результат на экране цифрового индикатора обновляется.
Следящий режим измерения.
Цикл измерения повторяется, после того как изменение измеряемой величины превысит ступень квантования.
Помимо погрешности измерения, к числу важных характеристик
ЦИП относится его быстродействие, время измерения и помехоустойчивость. Под быстродействием ЦИП понимается максимальной число измерений, выполняемых в единицу времени с нормированной погрешностью. Время измерения – интервал от начала цикла преобразования измеряемой величины до получения результата. Под помехоустойчивостью понимают способность ЦИП с нормированной погрешностью производить измерения при наличии помех.
Быстродействие ЦИП очень высокое. Современная элементная база позволяет строить ЦИП, обеспечивающие до 107
преобразований в секунду. Это, однако, оказывается излишним, поскольку регистрирующие устройства обеспечивают фиксацию не более 100 результатов измерений в секунду. При визуальном наблюдении требования к быстродействию резко снижаются, поскольку оператор способен оценить не более 2—3 результатов измерений в секунду.
2. Коды, применяемые в цифровых средствах измерений
Дискретизированные и квантованные значения функции в ЦИП кодируются. На рис.1,г показан унитарный код, при котором число передаваемых импульсов пропорционально квантованному значению измеряемой величины. Представление числового значения в унитарном коде имеет недостатки. Число импульсов в кодовых группах различно, чем больше представляемое число, тем больше импульсов содержит кодовая группа. Так, для представления числа 82 необходимо передать 82 импульса. Привычная для нас десятичная система счисления более экономна. Действительно, в ней для построения чисел используется десять цифр: 0, 1, 2, 3, .... 9. Число представляется в виде последовательности цифр. Каждая цифра занимает в нем определенную позицию (разряд). Например, число 482 содержит три цифры. Однако крайняя правая цифра 2 относится к разряду единиц, цифра 8 к разряду десятков, 4 – к разряду сотен. Таким образом, для представления данного числа в десятичной системе количество необходимых разрядов равно числу записанных цифр, т. е. трем. Запись этого же числа с помощью унитарного кода потребовала бы 482 импульса (знака). Экономность десятичной системы объясняется тем, то перемещение цифры влево на соседнюю позицию увеличивает ее значение в 10 раз. Цифра 10 является основанием десятичной системы счисления. Принципиально можно образовать систему счисления, используя любое число 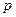 в качестве ее основания. в качестве ее основания.
Десятичная система позволяет легко выразить дробную часть величины. Для этого достаточно отделить целую часть запятой и цифры, записанные правее запятой, будут представлять десятые, сотые и т.д. доли. Прежде чем перейти к рассмотрению других систем счисления, рассмотрим позиционный принцип представления чисел с помощью ряда. В качестве примера используем число 482, 317:
482,317= 4·102
+8·101
+ 2·100
+ 3·10-1
+ 1·10-2
+7·10-3
.
Каждое слагаемое относится к определенному разряду, например 4·102
– к разряду сотен. Здесь 102
весовой коэффициент, а 4 – разрядный коэффициент. В общем случае число в произвольной системе счисления с основанием 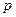 представляется рядом: представляется рядом:
 , (1) , (1)
где 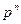 , , 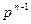 , ... , , ... , – весовые коэффициенты соответствующих разрядов, а – весовые коэффициенты соответствующих разрядов, а  , ,  , ... , , ... , 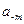 – разрядные коэффициенты. – разрядные коэффициенты.
Используя (1), можно на позиционном принципе строить различные системы счисления. Наибольший интерес для измерительной техники представляет двоичная система с основанием 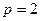 . Основное ее достоинство заключается в том, что для представления цифр разряда используется лишь два символа: 0 и 1. Например, число 11011,01 записано в двоичной системе счисления. Соответствующее ему число в привычной десятичной системе определяется с помощью (4.1): . Основное ее достоинство заключается в том, что для представления цифр разряда используется лишь два символа: 0 и 1. Например, число 11011,01 записано в двоичной системе счисления. Соответствующее ему число в привычной десятичной системе определяется с помощью (4.1):
11011,01 = 1·24
+1·23
+0·22
+1·21
+1·20
+0·2-1
+ 1·2-2
= 27,25.
Весовые коэффициенты разрядов, расположенных слева от запятой, равны соответственно 20
=1; 21
= 2; 22
= 4; 23
= 8, т. е. 1, 2, 4, 8, 16 и т. д. Таким образом, весовой коэффициент старшего разряда превышает весовой коэффициент предыдущего (младшего) разряда в 2 раза (а не в 10 раз, как в десятичной системе). Удобство применения двоичной системы счисления в цифровой технике связано с простотой построения запоминающих устройств (ЗУ). Хранить n-разрядные числа можно с помощью устройств, содержащих n элементов, каждый из которых запоминает соответствующую цифру числа. Для запоминания цифры каждого разряда двоичного числа могут использоваться устройства с двумя устойчивыми состояниями (триггеры). Одному из состояний триггера ставится в соответствие цифра 1, другому – 0.
Однако число, записанное в двоичной системе счисления, неудобно для визуального определения. Перевод его в десятичное число требует довольно сложных схем, поскольку нет непосредственной разбивки на десятичные разряды. По этой причине в ЦИП пользуются так называемым двоично-десятичным кодом. Двоично-десятичный код образуется путем представления каждой цифры десятичного числа соответствующим двоичным числом. Например, число 27 в десятичной системе преобразуется следующим образом. Цифра 2 записывается как 0010, а цифра 7 как 0111, т. е. 2710
=0010 01112/10
. Здесь индекс 10 свидетельствует о записи в десятичной системе, а 2/10 – в двоично-десятичной.
Отметим, что представление десятичного числа в двоично-десятичной системе с точки зрения числа символов менее экономно, чем в двоичной системе. Например, для числа 27 в двоично-десятичной системе надо иметь 8 символов, а в двоичной только 5 (11011). Но простота реализации ЦИП, работающих в двоично-десятичной системе, компенсирует этот недостаток.
В двоично-десятичном коде для представления каждой десятичной цифры используются четыре символа. Меньшим количеством обойтись нельзя, так как с помощью трех символов можно образовать лишь 8 комбинаций, а количество возможных цифр в каждом разряде десятичного числа равно 10 (0...9). Вместе с тем четыре символа (тетрада) позволяют построить 16 комбинаций, т. е. 6 комбинаций оказываются лишними. На первый взгляд вполне естественным кажется исключение тех комбинаций, которые выражают десятичные цифры более 9. Например, число 1011 равно 10, оно превышает возможный разрядный коэффициент в десятичной системе и может быть удалено. Код I, содержащий 10 начальных комбинаций (табл. 1)б соответствующих выражению цифр от 0 до 9 в двоичной системе счисления, называют кодом «8421». Однако он не является единственно возможным. Для каждой из десяти цифр вполне допустимо совершенно произвольное закрепление кодовых комбинаций. Поэтому число принципиально возможных тетрадно-десятичных кодов довольно велико. Код II в табл. 1 аналогичен коду I в пределах от 0 до 8, а число 9 закодировано с пропуском шести кодовых комбинаций. Это привело к невозможности выражения кода весами отдельных разрядов. Этот код называется символическим, в отличие от кода 1, который является позиционным. Код III также позиционный. Он имеет разрыв между числами 7 и 8, что меняет вес первого разряда. Его называют кодом «2421».
Таблица 1.

Код IV (код Айкена) имеет разрыв между цифрами 4 и 5. В этом месте проходит ось симметрии. Каждая кодовая комбинация над осью отличается от симметричной комбинации под осью инверсными значениями разрядных коэффициентов. Так десятичное число 3 воспроизводится кодовой комбинацией 0011. Симметрично расположенное относительно оси число 6 – комбинацией 1100. Эта комбинация может быть получена из 0011, если нули заменить единицами, а единицы нулями. Это свойство, называемое самодополнением, полезно при реализации арифметических операций с двоичными числами и, в частности, вычитания. ГОСТ 12814-74 рекомендует для использования в ЦИП тетрадно-десятичный код «2421».
  
        
     
      
      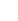 
   
    
   
    
5. Список использованной литературы
1. Б. П. Хромой, Ю.Г.Моисеев. Электрорадиоизмерения.
М.: «Радио и связь», 1985.
|