| САНКТ- ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ ФАКУЛЬТЕТ
Кафедра строительной механики и теории упругости
Контрольная работа
по дисциплине “Динамика сооружений”
Определение прогибов железобетонной балки и усилий в её сечениях при установившихся гармонических колебаниях
(шифр задания 3305)
Выполнил:
студент гр. 5015/10
Смирнов Д. В.
Преподаватель:
Константинов И. А.
С.-Петербург
2008 г.
Постановка задачи
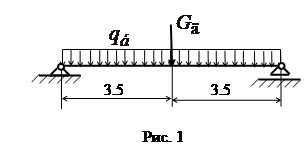
Дана железобетонная балка (рис. 1) со следующими параметрами: длина балки 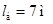 ; размеры прямоугольного поперечного сечения ; размеры прямоугольного поперечного сечения 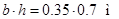 ; железобетон класса В25 (объемный вес ; железобетон класса В25 (объемный вес 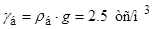 ; модуль упругости ; модуль упругости 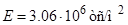 ). ).
В соответствии с заданными параметрами объем 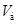 материала балки, площадь материала балки, площадь 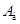 её поперечного сечения, полная масса её поперечного сечения, полная масса 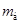 и её полный вес и её полный вес 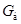 составляют соответственно величины: составляют соответственно величины: 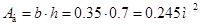 ; ; 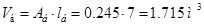 ; ; 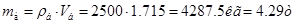 ; ; 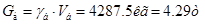 . .
По середине пролета балки расположен электродвигатель (он воздействует на балку силой 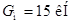 ; сила веса ротора ; сила веса ротора 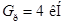 ; частота вращения ротора ; частота вращения ротора 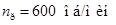 ). ).
На расчетной схеме балки для статического расчета ее вес представлен в виде равномерно распределенной нагрузки, а вес электромотора в виде сосредоточенной силы (см. рис. 1, а).
Расчетная схема для динамического расчета балки представляется в виде системы с одной степенью свободы. Такая расчетная схема получится (рис.1, б), если представить балку как систему двух элементов (тип 2 в программе SCAD) с узлами на опорах и по середине балки и заменить равномерно распределенную массу элементов двумя равными массами по концам элементов.
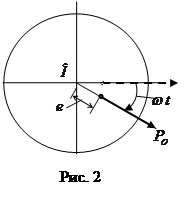
За возмущающую динамическую нагрузку, вызывающую поперечные колебания балки, в примере принята вертикальная составляющая центробежной силы (см. рис. 1, б), вызванной вращающимся ротором, имеющим эксцентриситет 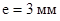 между центром массы ротора и его геометрической осью. между центром массы ротора и его геометрической осью.
Возмущающее гармоническое воздействие представляется в виде 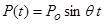 , где , где 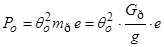 – амплитуда центробежной силы (рис. 2); – амплитуда центробежной силы (рис. 2); 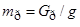 – масса ротора; – масса ротора;  – ускорение свободного падения. – ускорение свободного падения.
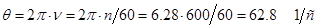
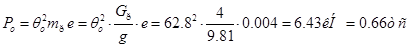
Требуется определить максимальный прогиб балки и максимальный изгибающий момент в ее среднем сечении:
· от статической нагрузки в виде собственного веса балки и электромотора;
· от динамической нагрузки в виде 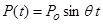 при установившихся гармонических колебаниях; при установившихся гармонических колебаниях;
· от суммарного воздействия обеих нагрузок
Статический и динамический расчет выполнить вручную и с помощью программы SCAD.
1 Выполнение задания при использовании для динамического расчета балки системы с одной степенью свободы
1.1 Расчет на ПК с использованием программы SCAD
1. Составляем расчетную схему балки для статического расчета и динамического расчета как системы с одной степенью свободы
С этой целью изобразим балку как систему двух элементов типа 2 (по классификации в программе SCAD) с узлами на опорах и в месте расположения двигателя (рис. 4).
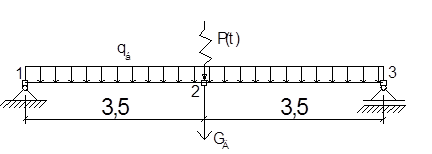
Рис. 4
На приведенной схеме показаны статические нагрузки от собственного веса балки и собственного веса двигателя и вертикальная составляющая динамической нагрузки, вызванной вращением ротора двигателя.
Так как мы рассматриваем эту систему как линейно деформируемую, то воспользуемся принципом независимости действия сил и определим прогибы балки и усилия в её сечениях отдельно от каждой нагрузки.
------------------------------------------------------------------------------------------
| Р А С П Р Е Д Е Л Е Н И Е В Е С О В М А С С |
------------------------------------------------------------------------------------------
| 1 2 3 |
------------------------------------------------------------------------------------------
| 3 - ( гарм-1) |
| Z 3.67 |
------------------------------------------------------------------------------------------
------------------------------------------------------------------------
|Загpу: N : COБCTB. : Ч A C T O T Ы : ПEPИOДЫ |
| : П/П : :-----------------------------:---------------|
|жение: : ЗHAЧEHИЯ : 1/C : ГЦ : C |
------------------------------------------------------------------------
| 3 1 .0093448 107.0104 17.03988 .0586858 |
------------------------------------------------------------------------
------------------------------------------------------------------------------------------
| Ф О Р М Ы К О Л Е Б А Н И Й |
------------------------------------------------------------------------------------------
| 1 2 3 |
------------------------------------------------------------------------------------------
| 3 - 1 ( гарм-1) |
| Z 1. |
------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
| И Н Е Р Ц И О Н Н Ы Е Н А Г Р У З К И |
------------------------------------------------------------------------------------------
| 1 2 3 |
------------------------------------------------------------------------------------------
| 3 - 1 ( гарм-1) |
| Z .988 |
| 3 - 2 |
| Z -.1356 |
Анализ результатов расчета
Прежде всего, отметим, что структура таблиц и их названия предназначены для систем с несколькими степенями свободы, что объясняет использование множественного числа в их названиях. В рассматриваемом примере имеем систему с одной степенью свободы.
Введенные результаты в первой и второй таблицах понятны: в первой – показано, что в узле 2 составленной расчетной схемы МКЭ находится сосредоточенная масса весом 3.67 тс; во второй – приведены результаты определения собственной круговой частоты ω, частоты f и периода T.
В третьей таблице для каждой собственной формы колебаний (СФК) отражаются относительные перемещения масс расчетной схемы по направлению их степеней свободы. При этом наибольшее перемещение в СФК принято равным единице. В рассматриваемом примере для системы с одной степенью свободы имеется только одна форма колебаний с одной ординатой, равной единице.
В четвертой таблице приведены амплитуды составляющих S1 и S2 суммарной силы S. Полная амплитуда So суммарной силы получается по формуле:
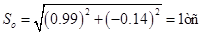
Аналогично, из таблиц для перемещений и для усилий в узле 2 загружения 3 соответственно получаем составляющие перемещения узла 3 расчетной схемы (см. рис. 1) и момента в этом сечении и максимальные значения этих величин:
| П Е Р Е М Е Щ Е Н И Я У З Л О В |
------------------------------------------------------------------------------------------
| 1 2 3 |
------------------------------------------------------------------------------------------
| 1 - ( СВ) |
| Z -.62551 |
| 2 - ( Вес двиг.) |
| Z -.357142 |
| 3 - 1 ( гарм-1) |
| Z -.230647 |
| 3 - 2 |
| Z .031663 |
------------------------------------------------------------------------------------------
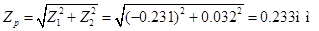
------------------------------------------------------------------------------------------
| У С И Л И Я /НАПРЯЖЕНИЯ/ В ЭЛЕМЕНТАХ |
------------------------------------------------------------------------------------------
| 2_ 1-1 1-2 1-3 2-1 2-2 2-3 |
| 1 1 1 2 2 2 |
| 2 2 2 3 3 3 |
------------------------------------------------------------------------------------------
| 1 - ( СВ) |
| M 2.81367 3.75156 3.75156 2.81367 |
| 2 - ( Вес двиг.) |
| M 1.33875 2.6775 2.6775 1.33875 |
| 3 - 1 ( гарм-1) |
| M .864582 1.72916 1.72916 .864582 |
| 3 - 2 |
| M -.118689 -.237378 -.237378 -.118689 |
| 3 - S1 |
| M .872691 1.74538 1.74538 .872691 |
------------------------------------------------------------------------------------------
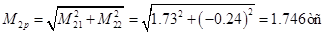
Контроль результатов расчетов на ПК с использованием известных формул для систем с одной степенью свободы
1. Определяем собственную частоту системы с одной степенью свободы
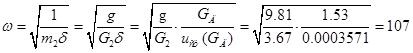 1/с. 1/с.
Здесь 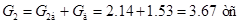 - вес массы, сосредоточенной в узле 2. - вес массы, сосредоточенной в узле 2.
2. Вычисляем динамический коэффициент 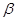 для двух вариантов решения задачи об установившихся колебаниях балки. для двух вариантов решения задачи об установившихся колебаниях балки.
Вариант 1 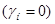 : :

Вариант 2  : :
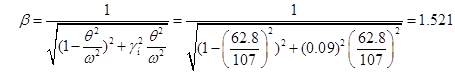
3. Вычисляем амплитуды искомых величин.
Амплитуда установившихся колебаний 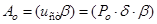 : :
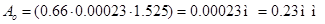
Величина 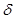 здесь получена пересчетом по прогибу здесь получена пересчетом по прогибу 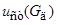 , подсчитанному выше от действия силы веса двигателя , подсчитанному выше от действия силы веса двигателя 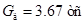 . .
Амплитуда суммарной силы для варианта 1: 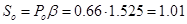 тс. тс.
Амплитуда изгибающего момента в среднем сечении балки для этого же варианта расчета:

4. Определяем суммарные значения искомых величин в среднем сечении балки с учетом знакопеременности динамических амплитуд, относящиеся к нижней и верхней сторонам балки:

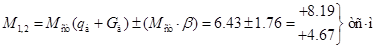
Полученные данные показывают, что в результате установившихся колебаний в балке максимальный во времени прогиб и изгибающий момент не изменяют знак, т.е. растянутой всегда будет нижняя сторона балки.
Как видим результаты расчетов вручную и с помощью ПК практически совпадают.
Эпюры изгибающих моментов при рассмотренных загружениях 1,2,3 соответственно изображены на рис. 3,а-3,г. В третьем (динамическом) загружении получаются две эпюры (рис. 3,в,г). Они соответствуют разложению суммарной нагрузки на колебания по синусу и косинусу. На рис. 3,д изображена эпюра расчетных изгибающих моментов при динамическом загружении, полученная по формуле для 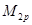 . .
Если предположить, что возмущающая частота совпала с собственной частотой системы (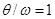 ), то коэффициент динамичности, амплитуда перемещений и амплитуда максимального изгибающего момента при резонансе получились бы соответственно равными: ), то коэффициент динамичности, амплитуда перемещений и амплитуда максимального изгибающего момента при резонансе получились бы соответственно равными:



Тогда соответствующие суммарные величины для прогиба и изгибающего момента в среднем сечении балки получились бы равными:
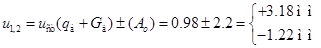
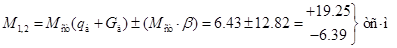
Полученные результаты показывают, что в результате установившихся колебаний в балке попеременно (с периодом 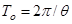 ) в среднем сечении максимальный во времени прогиб и максимальный изгибающий момент изменяют значения и знак, т. е. растянутыми будут то нижняя (знак +), то верхняя (знак − ), стороны балки. ) в среднем сечении максимальный во времени прогиб и максимальный изгибающий момент изменяют значения и знак, т. е. растянутыми будут то нижняя (знак +), то верхняя (знак − ), стороны балки.
Примерный вид эпюр изгибающих моментов в балке при установившихся колебаниях с коэффициентов динамичности 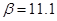 показан точечными линиями на рисунке 3,е. показан точечными линиями на рисунке 3,е.
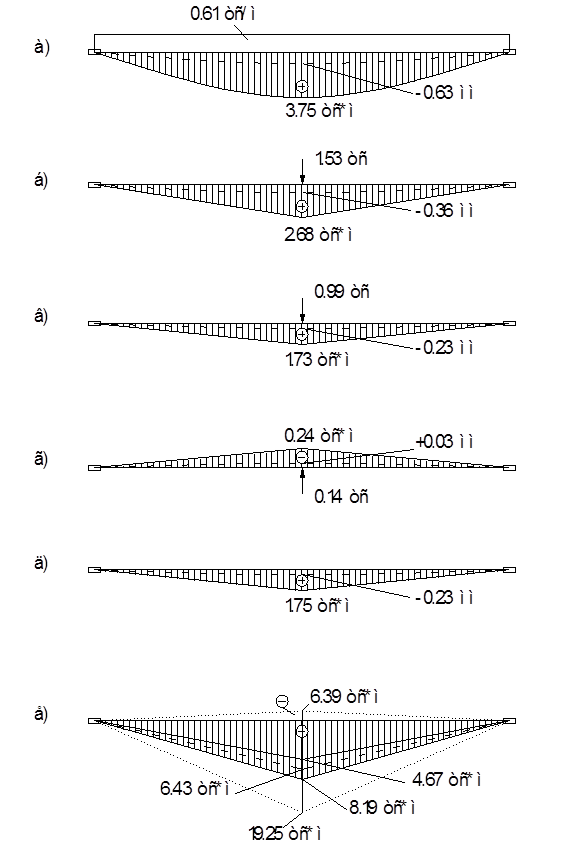
Рис. 3
2 Выполнение задания при использовании для динамического расчета балки системы с несколькими степенями свободы
2.1 Расчет на ПК с использованием программы SCAD
В варианте 1.1. задания 1 было рассмотрено решение задачи об определении максимального прогиба железобетонной балки с электродвигателем, расположенным по ее длине. Расчет выполнялся от двух статических и одного динамического загружений по расчетной схеме балки в виде системы с одной степенью свободы.
Рассмотрим решение этой же задачи с использованием расчетной схемы МКЭ, когда балка по длине пролета разделена на 4 равных конечных элемента типа 2. В этом случае при загружении узла 3 динамической нагрузкой получим расчетную схему в виде системы с тремя степенями свободы, которая может быть представлена в виде, приведенном на рис. 4.
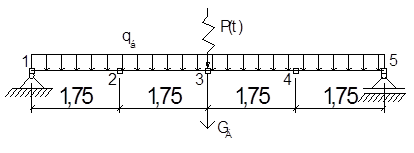
Рис. 4
Результаты расчета:
------------------------------------------------------------------------------------------
| Р А С П Р Е Д Е Л Е Н И Е В Е С О В М А С С |
------------------------------------------------------------------------------------------
| 1 2 3 4 5 |
------------------------------------------------------------------------------------------
| 3 - ( гарм-3) |
| Z 1.067 2.597 1.067 |
------------------------------------------------------------------------------------------
-----------------------------------------------------------------------------------|
|Загpу: N : COБCTB. : Ч A C T O T Ы : ПEPИOДЫ |
| : П/П : :-----------------------------:-------------- -|
|жение: : ЗHAЧEHИЯ : 1/C : ГЦ : C |
------------------------------------------------------------------------
| 3 1 .009285 107.7001 17.1497 .05831 |
| 2 .0017818 561.2033 89.36359 .0111902 |
| 3 .0012916 774.1783 123.2768 .0081118 |
------------------------------------------------------------------------
1-ая СФК

2-ая СФК
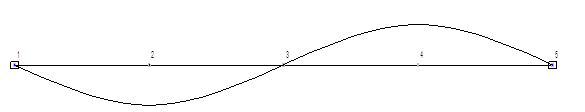
3-я СФК

------------------------------------------------------------------------------------------
| И Н Е Р Ц И О Н Н Ы Е Н А Г Р У З К И |
------------------------------------------------------------------------------------------
| 1 2 3 4 5 |
------------------------------------------------------------------------------------------
| 3 - 1 ( гарм-3) |
| Z .0665 .8888 .0665 |
| 3 - 2 |
| Z -.0152 -.1125 -.0152 |
------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
| П Е Р Е М Е Щ Е Н И Я У З Л О В |
------------------------------------------------------------------------------------------
| 1 2 3 4 5 |
------------------------------------------------------------------------------------------
| 1 - ( СВ) |
| Z -.445676 -.62551 -.445676 |
| 2 - ( Вес двиг.) |
| Z -.245535 -.357142 -.245535 |
| 3 - 1 ( гарм-3) |
| Z -.158161 -.228817 -.158161 |
| 3 - 2 |
| Z .021624 .03117 .021624 |
------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------
| У С И Л И Я /НАПРЯЖЕНИЯ/ В ЭЛЕМЕНТАХ |
------------------------------------------------------------------------------------------
| 2_ 1-1 1-2 2-1 2-2 3-1 3-2 4-1 4-2 |
| 1 1 2 2 3 3 4 4 |
| 2 2 3 3 4 4 5 5 |
------------------------------------------------------------------------------------------
| 1 - ( СВ) |
| M 2.81367 2.81367 3.75156 3.75156 2.81367 2.81367 |
| 2 - ( Вес двиг.) |
| M 1.33875 1.33875 2.6775 2.6775 1.33875 1.33875 |
| 3 - 1 ( гарм-3) |
| M .894092 .894092 1.6718 1.6718 .894092 .894092 |
| 3 - 2 |
| M -.125189 -.125189 -.223664 -.223664 -.125189 -.125189 |
| 3 - S1 |
| M .902814 .902814 1.6867 1.6867 .902814 .902814 |
------------------------------------------------------------------------------------------

Рис. 5
Расчет вручную.
Исходными данными для расчета вручную считаем определенные в результате модального анализа СЧ и СФК для рассматриваемой балки как системы с тремя степенями свободы.
1. Вычисление векторов инерционных сил в СФК
Вычисление для первой СФК (i=1)
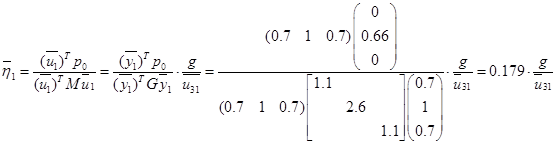
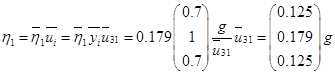
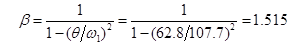
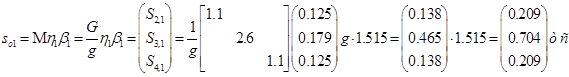
Вычисление для первой СФК (i=3)
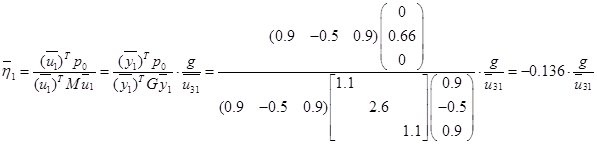
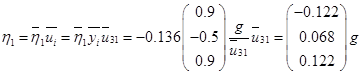
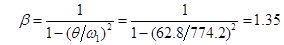
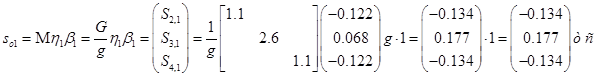
Результаты расчета сведем в таблицу 1.
Таблица 1
| 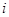
|
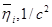
|
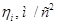
|
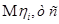
|
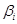
|
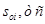
|
| 1
|
0.179
|
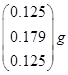
|
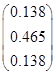
|
1.517
|
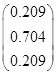
|
| 2
|
0
|
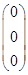
|
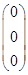
|
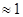
|
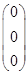
|
| 3
|
-0.136
|
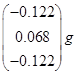
|
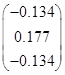
|
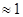
|

|
2. Выполнение контроля разложения вектора 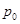 по СФК по СФК
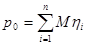
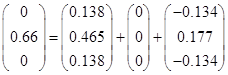
В данном случае проверка выполняется.
3. Вычисление перемещений и усилий в СФК в любом сечении 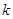 балки балки
Вектору инерциональных нагрузок 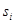 соответствует вектор прогибов балки соответствует вектор прогибов балки 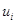 и усилия и усилия 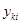 в любом сечении в любом сечении  . Для сокращения ручных вычислений ограничимся вычеслением прогиба и изгибающего момента только в среднем сечении балки. Результаты расчета сведем в таблицу 2. . Для сокращения ручных вычислений ограничимся вычеслением прогиба и изгибающего момента только в среднем сечении балки. Результаты расчета сведем в таблицу 2.
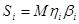 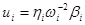
Таблица 2
4. Сопоставление суммарного вектора инерционных нагрузок по всем СФК
Этот вектор во всех СФК (при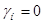 ) определяется при синусе равном 1. ) определяется при синусе равном 1.
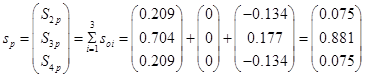 тс. тс.
В приведенной таблице результатов расчета инерционных сил в программе SCAD приводятся не векторы 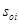 СФК, а векторы СФК, а векторы 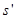 и и 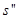 . Тогда расчетный вектор вычислим по формуле: . Тогда расчетный вектор вычислим по формуле:
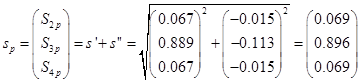 тс. тс.
Как видим, результаты практически совпали.
5. Вычисление расчетного изгибающего момента в среднем сечении балки
Суммирование амплитудных значений изгибающего момента, вычисленных в среднем сечении балки для всех трех СФК выполняется по формуле:
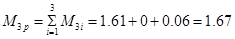 тс*м тс*м
В программе SCAD:
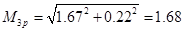 тс*м тс*м
Расчеты, выполненные в программе SCAD и вручную практически совпадают.
Сопоставления результатов расчета по двум расчетным схемам
Сопоставление результатов расчета рассматриваемой балки по определению её максимального прогиба и максимального изгибающего момента по рассмотренным 2 расчетным схемам показывает, что даже использование для динамического расчета расчетной схемы с одной степенью свободы дает удовлетворительные результаты.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Константинов И.А., Лалина И.И. Строительная механика. Расчет стержневых систем. Учеб. пособие. СПб.: Изд-во Политехн. ун-та. 2005. 155 с.
2. Константинов И.А. Строительная механика. Использование программы SCAD для расчета стержневых систем. Ч.I: Учеб. пособие. СПб.: Изд-во СПбГПУ, 2004. 81с.
3. Константинов И.А., Лалина И.И. Строительная механика. Использование программы SCAD для расчета стержневых систем. Ч.2: Учеб. пособие. СПб.:Изд-во Политехн. ун- та, 2005. 82с.
4. Лалин В.В., Константинов И.А., Лалина И.И.Динамика сооружений. Использование программы SCAD для решения задач динамики сооружений. Ч.1: Сайт каф. ЭиПГС, ФОДО,
2005. 92с.
|