Курсовая работа: Розвязання задачі Коші для звичайного диференціального рівняння першого порядку методом Ейлера
|
Название: Розвязання задачі Коші для звичайного диференціального рівняння першого порядку методом Ейлера Раздел: Рефераты по информатике Тип: курсовая работа |
| МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ Кафедра інформатикиКУРСОВА РОБОТАЗ програмування На тему: “Розв’язання задачі Коші для звичайного диференціального рівняння першого порядку методом Ейлера” Суми – 2006 р. План 1. Постановка задачі 2. Визначення. Загальні відомості про задачу Коші для звичайних диференціальних рівнянь першого порядку 3. Розв’язання задачі Коші для звичайних диференціальних рівнянь першого порядку методом Ейлера а) похибка при вирішенні задачі Коші для звичайних диференціальних рівнянь першого порядку методом Ейлера. Алгоритм розв’язання диференціального рівняння першого порядку методом Ейлера 4. Блок – схема 5. Реалізація алгоритму у середовищі Borland Pascal 6. Результат роботи програми 7. Умовні позначення 8. Список використаних джерел
Постановка задачі
ПОСТАНОВКА ЗАДАЧІ ТА МЕТОД ВИРІШЕННЯ Вирішити диференціальне рівняння чисельним методом ( у/ =f(x,y)) це означає для заданої послідовності аргументів х0 , х1 …, хn і числа у0 , не визначаючи функцію у=F(x),знайти такі значення у1 , у2 ,…, уn , що уi =F(xi )(i=1,2,…, n) і F(x0 )=y0 . Таким чином численні методи дозволяють замість знаходження функції У=F(x) отримати таблицю значень цієї функції для заданої послідовності аргументів. . Величина h=xk -xk-1 називаеться кроком інтегрування. Метод Ейлера відноситься до численних методів, що дають відповідь у вигляді таблиці наближених значень шуканої функціїу(х). він є порівняно грубим та використовуеться в основному для приблизних розрахунків. Визначення. Загальні відомості про задачу Коші для звичайних диференціальних рівнянь першого порядку Звичайним диференціальним рівнянням називається рівняння виду :
де порядок старшої похідної к називається порядком звичайного диференціального рівняння. Звичайне диференціальне рівняння має безліч розв’язків. Для знаходження хоча б одного розв’язку потрібні додаткові умови. Ці умови можуть бути двох типів – задача Коші та Краєва задача. Згідно теми курсової роботи розглянемо лише перший тип умови, тобто задачу Коші. При розв’язанні задачі Коші додаткові умови задаються при одному значенні незалежної змінної. Наприклад, при х = а задані значення функції 1. Апроксимація рядом Тейлора 2. Методи Рунне – Кутта 3. Методи прогнозу та корекції Нульовим наближенням всіх вище перерахованих методів вирішення задачі Коші є метод Ейлера. Розв ’ язання задачі Коші для звичайних диференціальних рівнянь першого порядку методом Ейлера Розглянемо найпростіший метод вирішення задачі Коші. Проілюструємо його на прикладі звичайного диференціального рівняння першого порядку.
Підстановка ПУ в початкове ЗДР* дає значення похідної
При цьому допускається похибка : Отже узагальнена формула методу Ейлера набуває вигляду:
Похибка, що допускається на кожному кроці :
Похибка при вирішенні задачі Коші для звичайних диференціальних рівнянь першого порядку методом Ейлера Для ЗДР першого порядку
Кали ми визначаємо приріст функції
та вводимо умовні позначення
то можливо оцінити
Якщо припустити, що початкова похибка рівна нулю, то випливає висновок :
Тепер, якщо замінити
З останнього співвідношення видно, що при
Мал. 1 На мал.1 приведені підрахунки для рівняння
Алгоритм розв’язання диференціального рівняння першого порядку методом Ейлера Нижче поданий алгоритм чисельно інтегрує звичайне диференціальне рівняння першого, другого та третього порядку з використанням модифікованого прямого методу Ейлера При чисельному інтегруванні диференціального рівняння першого порядку y' = F(x,y) З початковою умовою y(x0 ) = y0 (задача Коші) спочатку вибираємо порядок похідної – у нашому випадку згідно з варіантом курсової – порядок 1 (диференціальне рівняння першого порядку). Далі визначаємо коефіцієнти та коефіцієнт при х. Вводимо границі відрізку . Фіксований приріст аргументу h = (xf -x0 )/n, де xf - кінцева точка інтервалу інтегрування , n – кількість кроків. Потім, використовуючи процедуру модифікованого методу Ейлера, , обчислюємо yk згідно з рекурсивною формулою: yk = yk-1 +h[Fk-1 +F(xk , yk-1 +hFk-1 )]/2 де Fk = F(xk , yk ). Можна використовувати іншу рекурсивну формулу: yk = yk-1 +F(xk-1 +h/2, yk-1 +Fk-1 h/2) Після визначення кроку, вводимо значення початкової умови. Отримуємо таблицю відповідей.
Реалізація алгоритму у середовищі Borland Pascal uses wincrt; var yx,xy,l,v,p,ff,ay,by,x:array [0..10] of real; y,a,b:array[0..10,0..1] of real; i,n,o:integer; c,d,h,k:real; label lap1; begin clrscr; writeln('введите наивысший порядок производной (в нашем случае - 1)'); readln(n); if n=0 then begin writeln('это прямолинейная зависимость и решается без метода Эйлера'); goto lap1;end; writeln('введите коэффициенты {a0,a1}'); for i:=0 to n do readln(l[i]); if (n=1) and (l[1]=0) or (n=2) and (l[2]=0) or (n=3) and (l[3]=0) then begin writeln('деление на ноль'); goto lap1; end; writeln('введите коэффициент при x'); readln(k); writeln('введите отрезок '); readln(c,d); o:=5; h:=abs(d-c)/o; writeln('шаг=',h:1:1); writeln('задайте начальные условия y(x)= '); for i:=0 to n-1 do readln(v[i]); if n=3 then begin yx[0]:=v[0]; ay[0]:=v[1]; by[0]:=v[2]; p[0]:=(k*c-l[0]*v[0]-l[1]*v[1]-l[2]*v[2])/l[3]; x[0]:=c; gotoxy(32,1); write(' '); gotoxy(32,2); write(' x y a b '); gotoxy(32,3); write(' ',c:7:7,' ',yx[0]:7:7,' ',ay[0]:7:7,' ',by[0]:7:7,' '); for i:=0 to o-1 do begin x[i]:=x[i]+h/2; y[i,1]:=yx[i]+(h/2)*ay[i]; a[i,1]:=ay[i]+(h/2)*by[i]; b[i,1]:=by[i]+(h/2)*p[i]; ff[i]:=(k*x[i]-l[0]*y[i,1]-l[1]*a[i,1]-l[2]*b[i,1])/l[3]; xy[i]:=x[i]+h/2; yx[i+1]:=yx[i]+h*a[i,1]; ay[i+1]:=ay[i]+h*b[i,1]; by[i+1]:=by[i]+h*ff[i]; x[i+1]:=x[i]+h/2; p[i+1]:=(k*xy[i]-l[0]*yx[i+1]-l[1]*ay[i+1]-l[2]*by[i+1])/l[3]; end; for i:=0 to o-1 do begin gotoxy(32,4+i); write(' ',xy[i]:7:7,' ',yx[i+1]:7:7,' ',ay[i+1]:7:7,' ',by[i+1]:7:7,' '); end; gotoxy(32,4+o); write(' '); end; if n=2 then begin x[0]:=c; yx[0]:=v[0]; ay[0]:=v[1]; p[0]:=(k*c-l[0]*yx[0]-l[1]*v[1])/l[2]; gotoxy(32,1); write(' '); gotoxy(32,2); write(' x y a '); gotoxy(32,3); write(' ',c:7:7,' ',yx[0]:7:7,' ',ay[0]:7:7,' '); for i:=0 to o-1 do begin x[i]:=x[i]+h/2; y[i,1]:=yx[i]+(h/2)*ay[i]; a[i,1]:=ay[i]+(h/2)*p[i]; ff[i]:=(k*x[i]-l[0]*y[i,1]-l[1]*a[i,1])/l[2]; xy[i]:=x[i]+h/2; yx[i+1]:=yx[i]+h*a[i,1]; ay[i+1]:=ay[i]+h*ff[i]; x[i+1]:=x[i]+h/2; p[i+1]:=(k*xy[i]-l[0]*yx[i+1]-l[1]*ay[i+1])/l[2]; end; for i:=0 to o-1 do begin gotoxy(32,4+i); write(' ',xy[i]:7:7,' ',yx[i+1]:7:7,' ',ay[I+1]:7:7,' '); end; gotoxy(32,4+o); write(' '); end; if n=1 then begin x[0]:=c; yx[0]:=v[0]; p[0]:=(k*x[0]-l[0]*yx[0])/l[1]; for i:=0 to o-1 do begin x[i]:=x[i]+h/2; y[i,1]:=yx[i]+(h/2)*p[i]; xy[i]:=x[i]+h/2; ff[i]:=(k*x[i]-l[0]*y[i,1])/l[1]; yx[i+1]:=yx[i]+h*ff[i]; x[i+1]:=x[i]+h/2; p[i+1]:=(k*xy[i]-l[0]*yx[i+1])/l[1]; end; gotoxy(32,1); write(' '); gotoxy(32,2); write(' x____________ y '); write('___________________'); gotoxy(32,3); write(' ',c:7:7,' ',yx[0]:7:7,' '); for i:=0 to o-1 do begin gotoxy(32,4+i); write(' ',xy[i]:7:7,' ',yx[i+1]:7:7,' '); end; gotoxy(32,o+4); write(' '); end; lap1:readln; clrscr; end. Результат роботи програми
У випадку, коли порядок похідної = 0:
Умовні позначення 1. ПУ * - початкова умова 2. ЗДР* – звичайне диференціальне рівняння 3. ДР* - диференціальне рівняння Список використаних джерел :
Щодо реалізації алгоритму у середовищі Borland Pascal : · Боровик В.О., Тиркусова Н.В. програмування: Навч. посібник.-Суми: Вид-во СумДУ, 2004.-Частина 1.-107с. – Рос. Мовою · Боровик В.О., Тиркусова Н.В. програмування: Навч. посібник.-Суми: Вид-во СумДУ, 2004.-Частина 2.-107с. – Рос. Мовою · http:// www.forum.pascla.net · http://pascalclub.ru Щодо математичного обґрунтування методa: · Диференціальні рівняння : Навчю посібник А.М. Самійленко, С.А. Кривошия, М.О. Перестук. – К.: Либідь, 2003-504 с. · http:// www.alglib.sources.ru · http:// www.alglib.ru · http:// www.users.kpi.kharkov.ua |
 .
. 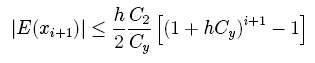 .
. 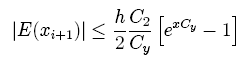 .
. 
 Блок - схема
Блок - схема

