Лабораторная работа: Измерение длины световой волны с помощью дифракционной решетки

Федеральное государственное образовательное учреждение

высшего профессионального образования

"Сибирский федеральный университет"

Институт градостроительства, управления и региональной экономики

Кафедра Физики

Отчет по лабораторной работе

Измерение длины световой волны с помощью дифракционной решетки

Преподаватель

В.С Иванова

Студент ПЭ 07-04

К.Н. Дубинская

Красноярск 2009

Цель работы

Изучение дифракции света на одномерной решетке, измерение длины световой волны.

Краткое теоретическое введение

Одномерная дифракционная решетка представляет собой ряд прозрачных параллельных щелей одинаковой ширины а, разделенных равными непрозрачными промежутками b. Сумму размеров прозрачного и непрозрачного участков принято называть периодом, или постоянной решеткой d.

d = a + b

Период решетки связан с числом штрихов на одном миллиметре n соотношением

d = 1/n

Общее число штрихов решетки N равно

N = 1/d = 1n

где l – ширина решетки.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех N щелей, т.е. дифракционная решетка осуществляет многолучевую интерференцию когерентных дифрагированных пучков света, идущих от всех щелей.

Пусть на решетку падает параллельный пучок монохроматического света с длиной волны 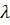. За решеткой в результате дифракции лучи будут распространяться по разным направлениям. Так как щели находятся на одинаковых расстояниях друг от друга, то разности хода ∆ вторичных лучей, образующихся согласно принципу Гюйгенса – Френеля и идущих от соседних щелей в одном направлении 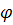, будут одинаковы в пределах всей решетки и равны

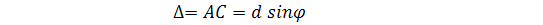
Если эта разность хода кратна целому числу длин волн, т.е.

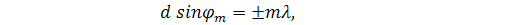
то при интерференции в фокальной плоскости линзы возникнут главные максимумы. Здесь m = 0,1,2, … - порядок главных максимумов.

Главные максимумы расположены симметрично относительно центрального, или нулевого, с m = 0, соответствующего лучам света, прошедшим через решетку без отклонений (недифрагированным, 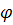= 0). Равенство (2) называют условием главных максимумов на решетке. Каждая щель также образует свою дифракционную картину. В тех направлениях, в которых одна щель дает минимумы, будут наблюдаться минимумы и от других щелей. Эти минимумы определяются условием

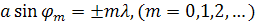
Положение главных максимумов зависит от длины волны λ. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (т = 0), разложатся в спектр, фиолетовая часть которого будет обращена к центру дифракционной картины, а красная - наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света, т.е. дифракционная решетка может быть использована как спектральный прибор.

Обозначим расстояние между серединой нулевого максимума и максимумами 1,2, ... m- го порядков, соответственно, х₁ х₂ ... х_т а расстояние между плоскостью дифракционной решетки и экраном -L. Тогда синус угла дифракции

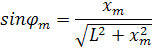
Используя последнее соотношение, из условия главных максимумов можно определить λ любой линии спектра.

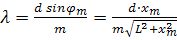
В экспериментальной установке имеются:

S- источник света, КЛ- коллиматорная линза, Щ- щель для ограничения размеров пучка света, ФЛ- фокусирующая линза, ДР- дифракционная решетка с периодом в = 0.01 мм, Э- экран для наблюдения дифракционной картины. Для работы в монохроматическом свете используются светофильтры.

Порядок выполнения работы

1. Расположим детали установки по 1 оси в указанном порядке, закрепляем на экране лист бумаги.

2. Включаем источник света S. Устанавливаем светофильтр белого цвета.

3. Измеряем прикрепленной к установке линейкой расстояние L от решетки до экрана.

L₁ = 13.5см=0.135м, L₂ =20.5см=0.205м.

4. Отмечаем на листе бумаги середины нулевого, первого и других максимумов вправо и влево от центра. С предельной точностью измерить расстояние х_1, х₂ .

5. Рассчитаем длины волн, пропускаемых светофильтром.

6. Найдем среднеарифметическое значение длины волны по формуле

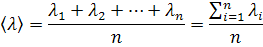
7. Рассчитаем абсолютную погрешность измерений по формуле

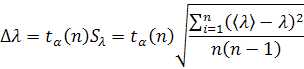
где n – число изменений, ɑ - доверительная вероятность измерения, t_ɑ (n) – соответствующий коэффициент Стьюдента.

8. Окончательный результат записываем в виде

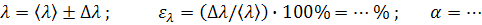
9. Сравниваем полученную длину волны с теоретическим значением. Записываем вывод по работе.

Ход работы