| Лабораторная работа 1
Численные методы решения
обыкновенных дифференциальных уравнений (4 часа)
При решении многих физических и геометрических задач приходится искать неизвестную функцию по данному соотношению между неизвестной функцией, ее производными и независимыми переменными. Такое соотношение называется дифференциальным уравнением
, а отыскание функции, удовлетворяющей дифференциальному уравнению, называется решением дифференциального уравнения.
Обыкновенным дифференциальным уравнением
называется равенство
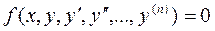 , (1) , (1)
в котором 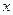 - независимая переменная, изменяющаяся в некотором отрезке - независимая переменная, изменяющаяся в некотором отрезке 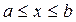 , а , а 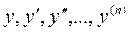 - неизвестная функция y
(
x
)
и ее первые n
производные. - неизвестная функция y
(
x
)
и ее первые n
производные.
Число 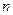 называется порядком уравнения
. называется порядком уравнения
.
Задача заключается в нахождении функции y, удовлетворяющей равенству (1). Более того, не оговаривая это отдельно, будем предполагать, что искомое решение обладает той или иной степенью гладкости, необходимой для построения и «законного» применения того или иного метода.
Различают два типа обыкновенных дифференциальных уравнений
- уравнения без начальных условий
- уравнения с начальными условиями.
Уравнения без начальных условий - это уравнение вида (1).
Уравнение с начальными условиями
- это уравнение вида (1), в котором требуется найти такую функцию 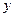 , которая при некотором , которая при некотором 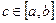 удовлетворяет следующим условиям: удовлетворяет следующим условиям:
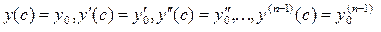 , ,
т.е. в точке 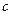 функция функция 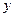 и ее первые и ее первые 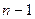 производных принимают наперед заданные значения. производных принимают наперед заданные значения.
Задачи Коши
При изучении способов решения дифференциальных уравнений приближенными методами основной задачей
считается задача Коши.
Рассмотрим наиболее популярный метод решения задачи Коши – метод Рунге-Кутта. Этот метод позволяет строить формулы расчета приближенного решения практически любого порядка точности.
Выведем формулы метода Рунге-Кутта второго порядка точности. Для этого решение представим куском ряда Тейлора, отбрасывая члены с порядком выше второго. Тогда приближенное значение искомой функции в точке x
1
можно записать в виде:
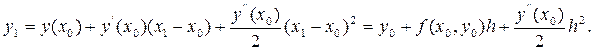 (2) (2)
Вторую производную y
"(
x
0
)
можно выразить через производную функции f
(
x
,
y
)
, однако в методе Рунге-Кутта вместо производной используют разность
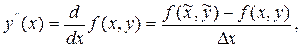
соответственно подбирая значения параметров 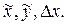
Тогда (2) можно переписать в виде:
y
1
=
y
0
+
h
[
β
f
(
x
0
,
y
0
) +
α
f
(
x
0
+
γh
,
y
0
+
δh
)],
(3)
где α
,
β
,
γ
и δ
– некоторые параметры.
Рассматривая правую часть (3) как функцию аргумента h
,
разложим ее по степеням h
:
y
1
=
y
0
+(
α
+
β
)
h
f
(
x
0
,
y
0
) +
αh
2
[
γ
fx
(
x
0
,
y
0
) +
δ
fy
(
x
0
,
y
0
)],
и выберем параметры α
,
β
,
γ
и δ
так, чтобы это разложение было близко к (2). Отсюда следует, что
α
+
β
=1,
αγ
=0,5,
α
δ
=0,5
f
(
x
0
,
y
0
).
С помощью этих уравнений выразим β
,
γ
и δ
через параметры α
,
получим
y
1
=
y
0
+
h
[(1 -
α
)
f
(
x
0
,
y
0
) +
α
f
(
x
0
+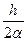 ,
y
0
+ ,
y
0
+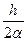 f
(
x
0
,
y
0
)],
(4)
f
(
x
0
,
y
0
)],
(4)
0 <
α
≤ 1.
Теперь, если вместо (x
0
,
y
0
) в (4) подставить (x
1
,
y
1
), получим формулу для вычисления y
2
–
приближенного значения искомой функции в точке x
2
.
В общем случае метод Рунге-Кутта применяется на произвольном разбиении отрезка [
x
0
,
X
]
на n
частей, т.е. с переменным шагом
x0
, x1
, …,xn
; hi
= xi+1
– xi
, xn
= X.
(5)
Параметры α
выбирают равными 1 или 0,5. Запишем окончательно расчетные формулы метода Рунге-Кутта второго порядка с переменным шагом для α
=1:
yi+1
=yi
+hi
f(xi
+
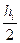 , yi
+
, yi
+
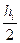 f(xi
, yi
)),
(6.1)
f(xi
, yi
)),
(6.1)
i
= 0,
1,…,
n
-1.
и α
=0,5:
yi+1
=yi
+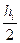 [f(xi
, yi
) + f(xi
+ hi
, yi
+ hi
f(xi
, yi
))],
(6.2) [f(xi
, yi
) + f(xi
+ hi
, yi
+ hi
f(xi
, yi
))],
(6.2)
i
= 0, 1,…,
n
-1.
Наиболее употребляемые формулы метода Рунге-Кутта – формулы четвертого порядка точности:
yi+1
=yi
+
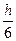 (k1
+ 2k2
+ 2k3
+ k4
),
(k1
+ 2k2
+ 2k3
+ k4
),
k1
=f(xi
, yi
), k2
= f(xi
+
 , yi
+
, yi
+
 k1
),
(7)
k1
),
(7)
k3
= f(xi
+
 , yi
+
, yi
+
 k2
), k4
= f(xi
+h, yi
+hk3
).
k2
), k4
= f(xi
+h, yi
+hk3
).
Для метода Рунге-Кутта применимо правило Рунге для оценки погрешности. Пусть y
(
x
;
h
)
– приближенное значение решения в точке x
,
полученное по формулам (6.1), (6.2) или (7) с шагом h
,
а p
–
порядок точности соответствующей формулы. Тогда погрешность R
(
h
)
значения y
(
x
;
h
)
можно оценить, используя приближенное значение y
(
x
; 2
h
)
решения в точке x
,
полученное с шагом 2
h
:
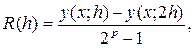 (8) (8)
где p
=2
для формул (6.1) и (6.2) и p
=4
для (7).
Уточненное решение пишем в виде
 . (9) . (9)
В алгоритмах с автоматическим выбором шага предварительно задают погрешность в виде положительного параметра ε, и на каждом этапе вычисления следующего значения yi
+1
подбирают такой шаг h
,
при котором выполняется неравенство
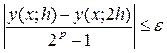 , (10) , (10)
Метод Рунге-Кутта применим и к задаче Коши для системы m
дифференциальных уравнений первого порядка с m
неизвестными функциями
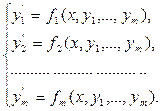 x x 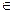 (x0
, X),
(11) (x0
, X),
(11)
y1
(x0
)=y1,0
, y2
(x0
)=y2,0
,…, ym
(x0
)=ym,0
.
(12)
Приведем для задачи (11), (12) расчетные формулы метода Рунге-Кутта четвертого порядка. Пусть требуется найти систему m
функций y
1
(
x
),
y
2
(
x
),…,
ym
(
x
),
удовлетворяющих в интервале (
x
0
,
X
)
дифференциальным уравнениям (11), а в точке x
0
– начальным условиям (12). Предположим, что отрезок [
x
0
,
X
]
разбит на N
частей:
xi
=
x
0
+
i
hi
, 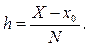
Тогда каждую l
-ю функцию yl
(
x
)
можно приближенно вычислять в точках xi
+1
по формулам Рунге-Кутта
Kl,1
=fl
(xi
, y1,i
, y2,i
,…,ym,i
), i=1, 2, …, m,
Kl,2
=fl
(xi
+  , y1,i
+ , y1,i
+  K1,1
, y2,i
+ K1,1
, y2,i
+  K2,1
,…,ym,i
+ K2,1
,…,ym,i
+  Km,1
), i=1, 2, …, m, Km,1
), i=1, 2, …, m,
Kl,3
=fl
(xi
+  , y1,i
+ , y1,i
+  K1,2
, y2,i
+ K1,2
, y2,i
+  K2,2
,…,ym,i
+ K2,2
,…,ym,i
+  Km,2
), i=1, 2, …, m,
(13) Km,2
), i=1, 2, …, m,
(13)
Kl,4
=fl
(xi
+ h, y1,i
+ hK1,3
, y2,i
+ hK2,3
,…,ym,i
+ hKm,3
), i=1, 2, …, m,
Yl,i+1
= yl,i
+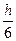 ( Kl,1
+ 2 Kl,2
+ 2 Kl,3
+ Kl,4
), i=1, 2, …, m, ( Kl,1
+ 2 Kl,2
+ 2 Kl,3
+ Kl,4
), i=1, 2, …, m,
Здесь через yl
,
i
обозначается приближенное значение функции yl
(
x
)
в точке xi
.
Обратите внимание
на порядок вычислений по формулам (13). На каждом шаге сначала вычисляются коэффициенты Kl
,
i
в следующем порядке:
K1,1
, K2
,1
,…, Km,1
,
K1,2
, K2
,2
,…, Km,2
,
K
1,3
,
K
2
,3
,…,
Km
,3
,
K
1,4
,
K
2
,4
,…,
Km
,4
,
и лишь затем приближенные значения функций y
1,
i
+1
,
y
2,
i
+1
,…,
ym
,
i
+1
.
Задачи Коши для дифференциальных уравнений n
-го порядка
y(n)
=f(x, y, y', …, y(n-1)
), x 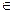 (x0
, X),
(14) (x0
, X),
(14)
y(x0
)=y0
, y'(x0
)=y1,0
, …, y(n-1)
(x0
)=yn-1,0
(15)
сводятся к задаче Коши для системы дифференциальных уравнений первого порядка с помощью замены переменных
z
0
=
y
,
z
1
=
y
',…
,
zn-1
=
y(n-1)
.
(16)
Учитывая (16), из уравнения (14) получим систему дифференциальных уравнений
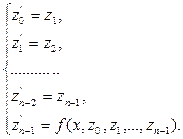 (17) (17)
Начальные условия (15) для функций zl
переписываются в виде
z0
(x0
)= y0
, z1
(x0
)= y1,0
,…, zn-1
(x0
)= y
п
-1,0
.
(18)
Запишем для полученной системы метод Рунге-Кутта:
zl,i+1
= zl,i
+
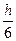 (Kl,1
+ 2Kl,2
+ 2Kl,3
+ Kl,4
),
(19)
(Kl,1
+ 2Kl,2
+ 2Kl,3
+ Kl,4
),
(19)
i
=0, 1, …,
N
,
l
=0, 1, …,
n
-1.
Для вычисления коэффициентов Kl
,1
,
Kl
,2
,
Kl
,3
и Kl
,4
имеем следующие формулы:
K
0,1
=
z
1,
i
,
K1
,1
=
z2
,
i,
…………
Kn-1,1
= f(xi
, z0,i
, z1,i
,…, zn-1,i
,),
K
0,2
=
z
1,
i
+
 K
1,1
, K
1,1
,
K1
,2
=
z2
,
i
+
 K2
,1
, K2
,1
,
…………………
Kn-1,2
= f(xi
+  , z0,i
+ , z0,i
+  K0,1
, z1,i
+ K0,1
, z1,i
+  K1,1
,…, zn-1,i
+ K1,1
,…, zn-1,i
+  Kn-1,1
), Kn-1,1
),
K0,3
= z
1,
i
+
 K
1,
2
, K
1,
2
,
K1,3
= z2,i
+  K2
,2
, K2
,2
,
……………………
Kn-1,3
= f(xi
+  , z0,i
+ , z0,i
+  K0,2
, z1,i
+ K0,2
, z1,i
+  K1,2
,…, zn-1,i
+ K1,2
,…, zn-1,i
+  Kn-1,2
), Kn-1,2
),
K0,4
= z1,i
+ hK1,3
,
K1,4
= z2,i
+ hK2,3
,
……………………
Kn-1,4
= f(xi
+ h, z0,i
+ hK0,2
, z1,i
+ hK1,2
,…, zn-1,i
+ hKn-1,2
).
Задания лабораторной работы 1
1. Написать файл-функции для решения поставленных далее задач.
2. Сохранить их в отдельных m-файлах (среда Матлаб)
3. Выполнить и оформить в виде отчета поставленные далее задачи.
Задача №
1
. Решить задачу Коши на отрезке [x0
,X] методом Рунге-Кутта четвертого порядка, применяя деление отрезка на N частей. Оценить погрешность.
Варианты заданий в табл.1.
Табл.1.
| № варианта
|
Уравнение 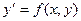
|
Начальное условие
|
[
x
0
,
X
]
|
N
|
| 1
|
y'(x)=sin(xy2
)
|
y(0)=1
|
[0,2]
|
10
|
| 2
|
y'(x)=cos(x) + y2
|
y(0)=2
|
[0,2]
|
20
|
| 3
|
y'(x)= cos(xy2
)
|
y(0)=3
|
[0,2]
|
30
|
| 4
|
y'(x)=sin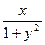
|
y(0)=1
|
[0,2]
|
40
|
| 5
|
y'(x)=tg 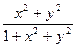
|
y(0)=2
|
[0,2]
|
50
|
| 6
|
y'(x)=x + y2
|
y(1)=3
|
[1,2]
|
10
|
| 7
|
y'(x)= 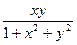
|
y(1)=1
|
[1,2]
|
20
|
| 8
|
y'(x)=cos 
|
y(1)=2
|
[1,2]
|
30
|
| 9
|
y'(x)=sin
(
x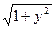 )
)
|
y(1)=3
|
[1,2]
|
40
|
| 10
|
y'(x)= 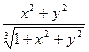
|
y(1)=1
|
[1,2]
|
50
|
| 11
|
y'(x)=x ln(1+y2
)
|
y(1)=2
|
[1,3]
|
10
|
| 12
|
y'(x)=y cos(x+y2
)
|
y(1)=3
|
[1,3]
|
20
|
| 13
|
y'(x)=ex
x+y2
|
y(1)=1
|
[1,3]
|
30
|
| 14
|
y'(x)=sin(x(1+y2
))
|
y(1)=2
|
[1,3]
|
40
|
| 15
|
y'(x)=lg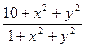
|
y(1)=3
|
[1,3]
|
50
|
| 16
|
y'(x)=x+y2
3x
|
y(-1)=1
|
[-1,1]
|
10
|
| 17
|
y'(x)=|x-y|(1+x2
+y2
)
|
y(-1)=2
|
[-1,1]
|
20
|
| 18
|
y'(x)= 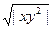
|
y(-1)=3
|
[-1,1]
|
30
|
| 19
|
y'(x)=x+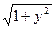
|
y(-1)=1
|
[-1,1]
|
40
|
| 20
|
y'(x)=
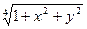
|
y(-1)=2
|
[-1,1]
|
50
|
| 21
|
y'(x)= 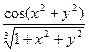
|
y(0)=3
|
[0,π]
|
10
|
| 22
|
y'(x)=sin(x) ln(1+y2
)
|
y(0)=1
|
[0,π]
|
20
|
| 23
|
y'(x)=sin(y) cos(x+y2
)
|
y(0)=2
|
[0,π]
|
30
|
| 24
|
y'(x)=ex
sin(y)+x2
ey
|
y(0)=3
|
[0,π]
|
40
|
| 25
|
y'(x)= cos(x) (x+y2
)
|
y(0)=1
|
[0,π]
|
50
|
| 26
|
y'(x)= 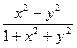
|
y(
π/2
)=2
|
[π/2,π]
|
10
|
| 27
|
y'(x)=x 2y+y 2x
|
y(
π/2
)=1
|
[π/2,π]
|
20
|
| 28
|
y'(x)= |x - y| cos(x2
+ y2
)
|
y(
π/2
)=3
|
[π/2,π]
|
30
|
| 29
|
y'(x)= 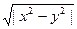
|
y(
π/2
)=2
|
[π/2,π]
|
40
|
| 30
|
y'(x)=(y + x 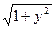 ) )
|
y(
π/2
)=3
|
[π/2,π]
|
50
|
Задача №
2
. Решить задачу Коши для дифференциального уравнения сведением к задачи Коши для системы уравнений первого порядка.
Табл.2.
| № варианта
|
Дифференциальное уравнение
|
Начальное условие
|
[
x
0
,
X
]
|
N
|
| 1
|
y(x)=x y(x)+ sin(x)
|
y
(0)=1,
y'
(0)
=2
|
[0,2]
|
10
|
| 2
|
y"'(x)=2x2
y(x) y"(x)
|
y(0)=2,
y'
(0)
=2,
y"(0)=1
|
[0,2]
|
20
|
| 3
|
y"(x) – 3cos(x) y(x)=tg(x)
|
y(0)=3,
y'
(0)
=2
|
[0,2]
|
30
|
| 4
|
"'y(x)=x y'(x)
|
y(0)=1,
y'
(0)
=1,
y"(0)=1
|
[0,2]
|
40
|
| 5
|
y"'(x)=-cos(x) y"(x) – y(x) sin(x)
|
y(0)=2,
y'
(0)
=2
,
y"(1)=1
|
[0,2]
|
50
|
| 6
|
y"(x)– sin(x) y(x)=sin(x)
|
y(1)=3,
y'
(
1
)
=1
|
[1,2]
|
10
|
| 7
|
y"(x) – 2x2
y(x)=cos(x)
|
y(1)=1,
y'
(
1
)
=1
|
[1,2]
|
20
|
| 8
|
y"'(x)=(x – 1) y(x) + x y"(x)
|
y(1)=2,
y'
(
1
)
=1,
y"(1)=1
|
[1,2]
|
30
|
| 9
|
y"(x) - sin(x) y(x)=sin3
(x)
|
y(1)=3,
y'
(
1
)
=1
|
[1,2]
|
40
|
| 10
|
y"'(x)=x y(x) - sin(x) y'(x)
|
y(1)=1,
y'
(
1
)
=1,
y"(1)=1
|
[1,2]
|
50
|
| 11
|
y"(x)-cos(x) y(x)=x
|
y(1)=2,
y'
(
1
)
=1
|
[1,3]
|
10
|
| 12
|
y"'(x) – 2x2
y(x)=x2
|
y(1)=3,
y'
(0)
=1,
y"(0)=1
|
[1,3]
|
20
|
| 13
|
y"(x) - lgx y(x)=2x
|
y(1)=1,
y'
(
1
)
=1
|
[1,3]
|
30
|
| 14
|
y"'(x) - 2|sin(x)| y'(x)=3x3
|
y(1)=2,
y'
(
1
)
=1,
y"(1)=1
|
[1,3]
|
40
|
| 15
|
y"(x) – 2lnx y(x)=1+x
|
y(1)=3,
y'
(
1
)
=1
|
[1,3]
|
50
|
| 16
|
y"'(x) - |cos(x)| y(x)=x
|
y(-1)=1,
y'
(
-1
)
=1,
y"(-1)=1
|
[-1,1]
|
10
|
| 17
|
y"(x) - 2|x| y(x)=cos2
(x)
|
y(-1)=2,
y'
(
1
)
=1
|
[-1,1]
|
20
|
| 18
|
y"'(x) - y(x)=e2x
|
y(-1)=3,
y'
(
-1
)
=1,
y"(-1)=1
|
[-1,1]
|
30
|
| 19
|
y"(x) – ln(1+x2
) y(x)=sin(2x)
|
y(-1)=1,
y'
(
1
)
=1
|
[-1,1]
|
40
|
| 20
|
y"'(x) – sin|x| y(x)=sin(x)
|
y(-1)=2,
y'
(
-1
)
=1,
y"(-1)=1
|
[-1,1]
|
50
|
| 21
|
y"(x) - 2y(x)=sin(x)
|
y(0)=3,
y'
(0)
=2
|
[0,π]
|
10
|
| 22
|
y"'(x)=3y(x)+y"(x) cos(x)
|
y(0)=1,
y'
(0)
=1,
y"(0)=1
|
[0,π]
|
20
|
| 23
|
y"(x) - 2x y(x)=x3
|
y(0)=2,
y'
(0)
=2
|
[0,π]
|
30
|
| 24
|
y"'(x) - x y(x)=x4
y'(x)
|
y(0)=3,
y'
(0)
=1,
y"(0)=1
|
[0,π]
|
40
|
| 25
|
y"(x) - 2x2
y(x)=x2
|
y(0)=1,
y'
(0)
=2
|
[0,π]
|
50
|
| 26
|
y"'(x)=cos(x) y(x)+ex
y"(x)
|
y(
2
)=2,
y'
(
2
)
=1,
y"(2)=1
|
[2,π]
|
10
|
| 27
|
y"(x) - 2x2
y(x)=2x ex
|
y(
2
)=3,
y'
(0)
=2
|
[2,π]
|
20
|
| 28
|
y"'(x) - 5y"(x)=32x
|
y(
2
)=1,
y'
(
2
)
=1,
y"(2)=1
|
[2,π]
|
30
|
| 29
|
y"(x) - 2sin(x) y(x)=sin(3x)
|
y(
2
)=2,
y'
(0)
=2
|
[2,π]
|
40
|
| 30
|
y"'(x) - lnx y'(x)=1
|
y(
2
)=3,
y'
(
2
)
=1,
y"(2)=1
|
[2,π]
|
50
|
Задача №
3
.
Найти методом Рунге-Кутта с точностью ε = 10-8
решение задачи Коши y
'(
x
)=2
x
(1+
y
2
),
y
(0)=0
в точке x
=1
.
(Точным решением является функция y
(
x
)=
tg
(
x
2
)
)
Задача №
4
.
Решить методом Эйлера на отрезке [1, 2] задачу Коши
y
'(
x
)=
 ,
y
(1)=0.
,
y
(1)=0.
(Точным решением данной задачи является функция y
(
x
)=
tg
(
ln ).
).
Контрольные вопросы:
1. Какое уравнение называется обыкновенным дифференциальным уравнением?
2. Какие методы решения задач для дифференциальных уравнений вы знаете?
3. В каком случае решение дифференциального уравнения единственно?
4. Рассказать правило Рунге для оценки погрешности.
|