Учебное пособие: Система оценивания по математике и информатике
|
Название: Система оценивания по математике и информатике Раздел: Рефераты по педагогике Тип: учебное пособие | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Контроль и оценка знаний и умений учащихся средней школы образовательной области математика 1.1 Контроль и оценка знаний и умений учащихся по математике Цель проверки знаний и умений учащихся: проверка качества усвоения знаний и умений учащихся. Таблица 1.
Таблица 2. Соотношение баллов и отметки при оценке заданий на трех уровнях требований к знаниям и умениям учащихся
Реализация экологической направленности в обучении школьников ведется по программам с вариативным компонентом. Контрольная работа по математике: 9 класс, нулевой срез, 2004-2005 учебный год.Учитель высшей категории М.Ю.Симатова 1 вариант.Уровень А (репродуктивный). 1. Найдите значение выражения А. 2. Чему равно произведение (1,6 × 10–8 )×(4 × 104 )? А. 0,064 Б. 0,000064 В. 0,00064 Г. 640 3. Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет? А. 960 р. Б. 820 р. В. 160 р. Г. 1600 р. 4. Из формулы пути равноускоренного движения А. t
= 5. Стоимость a карандашей равна х р. Сколько стоят b таких же карандашей? А. a
х
b
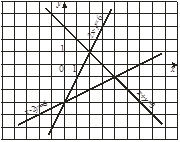
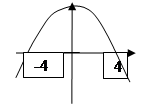
Б. 6. Укажите выражение, тождественно равное многочлену 6a – 8ab . А. –2a (3 – 4b ) Б. –2a (3 + 4b ) В. –2a (4b – 3) Г. –2a (–3 – 4b ) 7. Выполните действие: А. 8. Решите уравнение 10 – 7х = 3 – 2(5х + 1). А. –2,25 Б. –5,5 В. –3 Г. 6 9. В цирке перед началом представления было продано А. 40 Б. 80 В. 120 Г. 160 Уровень В (конструктивный). 10. Найдите корни уравнения 32 – 2х 2 = 0. Ответ : __________________________ 11. Пользуясь рисунком, решите систему уравнений
А. (2; 1) Б. (4; –1) В. (0; –3) Г. (–1; 4) 12. На координатной прямой отмечены числа a , b и c . Какое из приведенных утверждений об этих числах неверно? А. ab < 0 Б. b – c < 0 В. b + a > 0 Г. abc < 0 13. На каком рисунке изображено решение неравенства 2х + 3 ³ 6х – 5? А. В. Б. Г. 14. Установите соответствие между графиками функций и формулами.
1.2. 3.4 A. у
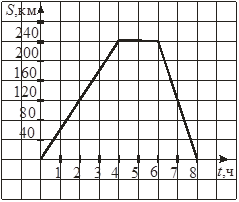
= 15.На рисунке изображен график движения автобуса от одного города до другого и обратно. На сколько километров в час автобус увеличил скорость на обратном пути?
А. 10 км/ч. Б. 20 км/ч. В. 60 км/ч. Г. 30 км/ч. Уровень С (творческий). 1. Упростите выражение:
2. Токарь должен изготовить 80 одинаковых деталей. Он увеличил норму выработки на одну деталь в день. В результате он закончил работу на 4 дня раньше срока. Сколько деталей в день по плану должен был делать токарь? 3. На каждого жителя города Челябинска ежесуточно выбрасывается 3,5 кг вредных веществ. Какое количество вредных веществ в год выбрасывается на всех жителей города Челябинска, если сейчас в нём проживает 1,2 миллиона человек? Результат представить в стандартном виде. Спрогнозируйте ситуацию на 10 лет. 4. Найдите значение m, при котором точки А(-3;18), В(0;-6), С(m;-2) лежат на одной прямой. Вариант 2. Уровень А (репродуктивный). 1. Найдите значение выражения А. 2. Чему равно произведение (1,2 × 10–8 )×(3 × 104 )? А. 0,036 Б. 0,000036 В. 0,00036 Г. 360 3. Сберегательный банк начисляет на срочный вклад 30% годовых. Вкладчик положил на счет 900 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет? А. 1270 р. Б. 270 р. В. 7200 р. Г. 1170 р. 4. Из формулы пути равноускоренного движения А. t
= 5. Стоимость a карандашей равна у р. Сколько стоят b таких же карандашей? А. a
у
b
Б. 6. Укажите выражение, тождественно равное многочлену 4a2 -8ab. А. –4a(a– 4b ) Б. –4a (a + 4b ) В. –4a (2b – a) Г. –4a (a – 2b ) 7. Выполните действие: А. 8. Решите уравнение 10 – 3х = 5 – 2(3х - 1). А. –1,25 Б. –5,5 В. –1Г. 6 9. В цирке перед началом представления было продано А. 40 Б. 240 В. 24 Г. 160 Уровень В (конструктивный). 10. Найдите корни уравнения 64 – 4х 2 = 0. Ответ : __________________________ 11. Пользуясь рисунком, решите систему уравнений
А. (2; 1) Б. (4; –1) В. (0; –3) Г. (–1; 4) 12. На координатной прямой отмечены числа a , b и c . Какое из приведенных утверждений об этих числах неверно?
А. ab < 0 Б. b – c < 0 В. b + a < 0 Г. abc > 0 13. На каком рисунке изображено решение неравенства 2х + 3 ³ 6х – 5? А. В. Б. Г. 14. Установите соответствие между графиками функций и формулами.
1.2. 3 A. у
=- 15.На рисунке изображен график движения автобуса от одного города до другого и обратно. На сколько километров в час автобус увеличил скорость на обратном пути?
А. 60 км/ч. Б. 20 км/ч. В. 10 км/ч. Г. 30 км/ч. Уровень С (творческий). 1. Упростите выражение:
2. Бригада рабочих должна была за определенный срок изготовить 768 пылесосов. Первые пять дней бригада выполняла ежедневно установленную норму, а затем каждый день изготовляла на 6 пылесосов больше, чем намечалось, поэтому уже за день до срока было изготовлено 844 пылесоса. Сколько пылесосов в день должна была изготовить бригада по плану? 3.На каждого жителя города Магнитогорска ежесуточно выбрасывается 5 кг вредных веществ. Какое количество вредных веществ в год выбрасывается на всех жителей города Челябинска, если сейчас в нём проживает 0,8 миллиона человек? Результат представить в стандартном виде. Спрогнозируйте ситуацию на 10 лет. 4. Найдите значение m, при котором точки А(-3;18), В(0;-6), С(2;-m) лежат на одной прямой. Контрольная работа по алгебре: 9 класс, промежуточный срез, 2004-2005 учебный год.Учитель высшей категории М.Ю.Симатова 1 вариант. Уровень А (репродуктивный). 1. На каком из рисунков изображен график квадратичной функции:
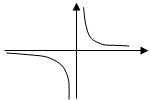
А) Б) В) 2. Функция задана формулой f(x)=-3х2 +5х-2. Найдите f(1/2). а) 1; б) -1/4;в) Ѕ. 3. На каком из рисунков изображен график функции у=
а)б)в) 4. Найдите нули функции у= a) Нулей нет;б) 3 и -5;в) -3 и 5. 5. Какие из линейных функций являются убывающими: у=7-2х; у=3х; у=-2; у=-5х+7. а) у=7-2х, у=-5х+7;б) у=-5х+7, у=-2;в) у=7-2х, у=-2, у=-5х+7. Уровень В (конструктивный). 6. Найдите корни квадратного трехчлена –х2 +4х-3: а) 1 и 3;б) -3 и 1;в) -5 и -3. 7. Разложите на множители квадратный трехчлен 6-7х+х2 . а) -7(х-6)(х-1);б) (х+1)(х+6);в) (х-1)(х-6). 8. Сократите дробь ответ: _________________. 9. Решить неравенство Х2 -2х-8<0. Ответ: _________________. 10. Найдите нули функции у=х3 +2х2 -х-2. Ответ: ___________________. Часть С (творческий). 11. Решить неравенство 12. Постройте график функции у=х2 +2х-3. 13. Найдите область определения функции 14. Периметр прямоугольника равен 22 см, а его площадь равна 30 см2 . Найдите стороны прямоугольника. 15. Определите значение х, при котором функция у=-х2 +2х-1 принимает наибольшее значение. Найдите это значение. 2 вариант. Уровень А (репродуктивный). 1. На каком из рисунков изображен график квадратичной функции:
А) Б) В) 2. Функция задана формулой f(x)=3х2 -5х-2. Найдите f(2). а) -6; б) 0;в) -24. 3. На каком из рисунков изображен график функции у=х3 :
а)б)в) 4. Найдите нули функции у= a) Нулей нет;б) 4 и -6;в) -4 и 6. 5. Какие из линейных функций являются убывающими: у=3-4х; у=5х; у=5; у=-9х+2. а) у=3-4х, у=-9х+2;б) у=-9х+2, у=5;в) у=3-4х, у=5, у=-9х+2. Уровень В (конструктивный). 6. Найдите корни квадратного трехчлена –х2 +3х-10: а) 2 и 5;б) -2 и 5;в) -5 и -2. 7. Разложите на множители квадратный трехчлен 15-8х+х2 . а) -8(х-5)(х-3);б) (х+5)(х+3);в) (х-5)(х-3). 8. Сократите дробь 9. Решить неравенство 3х2
-4х+1 10. Найдите нули функции у=х3 -х2 -9х+9. Ответ: ___________________. Часть С (творческий). 11. Решить неравенство 12. Постройте график функции у=х2 -2х-3. 13. Найдите область определения функции 14. Периметр прямоугольника равен 18 см, а его площадь равна 20 см2 . Найдите стороны прямоугольника. 15. Определите значение х, при котором функция у=-х2 -6х-9 принимает наибольшее значение. Найдите это значение. Итоговая контрольная работа по алгебре, 9 класс, 2004-2005 учебный год. Уровень требований - низкий. Учителя высшей категории: Н.П.Карпенко, Г.А. Кузнецова., И.Г. Сазыкина 1 вариант. Уровень А (репродуктивный). Заполните пропуски: 1. Функцией называют такую зависимость переменной ______ от переменной _______ , при которой каждому значению переменной _____ соответствует единственное значение переменной _____. 2. Все значения независимой переменной образуют область __________________ функции. 3. Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует _______________ значение функции. 4. Корнем n-й степени из числа а называется такое число _______________, степень которого равна _____________. 5. Геометрической прогрессией называют последовательность отличных от нуля чисел, каждый член которой, начиная со второго равен предыдущему члену, _____________ на одно и то же число. Уровень В (конструктивный). 1. Среди выражений выбери ту функцию, которая является квадратичной: а) у=2х+3;б) у= 2. Схематически изобразите график квадратичной функции. 3. Функция здана формулой у= -2х+1. Найдите значений функции при х=2. а) 5;б) 3;в) -3;г) -5. 4. Проходит ли график функции у= а) (4; 0);б) (1; -0,25);в)(-1; 0,25);г) (0; 4). Ответ: ___________________________. 5. При каких значениях х функция принимает отрицательные значения
а) (4; -4);б) (0; 6);в) (0; 3);г) (-4; 4). Ответ: ____________________________. 6. Составьте формулу n-го члена арифметической прогрессии а1 =2,4; d=-0,8. а) аn =2n-6;б) аn =2n-2;в) аn =2n-5;г) аn =2n-3. 7. Найдите сумму первых пяти членов арифметической прогрессии а1 =-4; d=2. а) 0;б) -40;в) -32;г) 10. 8. Вычислите а) -6;б) 6;в) 0;г) -2. 9. Вычислите а) 25,1;б) 25,2;в) 0,14;г) -2. 10. Решите уравнение 1) х4 =625 а) 5;б) -5; 5;в) 25;г) -25. 2) х3 +7=0 а) Уровень С (творческий). 1. Среди выражений выберите те, которые являются функциями а) х2
-3=0;б) у= 2. Постройте график функции у=-х2 -3х+4. 3. Решите неравенство (х-3)(х+5)>0. 4. Сократите дробь 5. Периметр прямоугольника равен 22 см, а его площадь равна 30 см2 . Найдите стороны прямоугольника. 2 вариант. Уровень А (репродуктивный). Заполните пропуски: 1. Функцией называют такую зависимость переменной ______ от переменной _______ , при которой каждому значению переменной _____ соответствует единственное значение переменной _____. 2. Все значения, которые принимает зависимая переменная образуют область __________________ функции. 3. Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует ________________ значение функции. 4. Арифметическим корнем n-й степени из неотрицательного числа а называется такое число _______________, n –я степень которого равна _____________. 5. Арифметической прогрессией называют последовательность отличных от нуля чисел, каждый член которой, начиная со второго равен предыдущему члену, _____________ с одним и тем же числом. Уровень В (конструктивный). 2. Среди выражений выбери ту функцию, которая является линейной: а) у=х-5;б) у= 2. Схематически изобразите график линейной функции. 3. Функция задана формулой у= х2 +1. Найдите значений функции при х=-1. а) -2;б) 2;в) 0;г) -1. 4. Проходит ли график функции у= а) (0; 0);б) (-1; -1/3);в)(0; 3);г) (1; -1/3). Ответ: ___________________________. 5. При каких значениях х функция принимает положительные значения
а) (-2; 4);б) (-2; 1);в) (0; 4);г) (1; 4). Ответ: ____________________________. 6. Составьте формулу n-го члена геометрической прогрессии b1 =48; q=0,5. а) bn =-1+3n -1 ;б) bn =-3n -1 ;в) bn =-1+3n ;г) bn =-1•3n +1 7. Найдите сумму первых пяти членов геометрической прогрессии а1 =-1; q=3. а) -3;б) 20,25;в) -20,25;г) 20. 8. Вычислите а) 1;б) -1;в) -5;г) 5. 9. Вычислите а) 9,2;б) 9,4;в) 3,2;г) 10. Решите уравнение 1) х6 =64 а) 2;б) -2; 2;в) 8;г) -8. 2) х5 +5=0 а) Уровень С (творческий). 1. Среди выражений выберите те, которые являются функциями а) у=х2 ;б) 2х-3=0;в) х2 =4;г) (х-1)2 . 2. Постройте график функции у=х2 +3х-4. 3. Решите неравенство (х-8)(х+4)>0. 4. Сократите дробь 5. Периметр прямоугольника равен 18 см, а его площадь равна 20 см2 . Найдите стороны прямоугольника. Уровень требований - средний. 1 вариант. Уровень А (репродуктивный). Заполните пробелы: 1. Функция называется возрастающей в некотором промежутке, если _______ значению аргумента из этого промежутка соответствует _______; 2. Квадратным трехчленом называется многочлен вида _________________, где х-переменная, а, b и с - _______________________________________________, причем а≠0; 3. Арифметической прогрессией называют _____________________________, каждый член которой, _______________________________ равен предыдущему члену, ____________________________________; 4. Записать формулу n-го члена арифметической прогрессии и формулу суммы n первых членов арифметической прогрессии; 5. Функция y=f(x) называется четной, если область ее определения ________________ и для любого значения аргумента х верно равенство ___________________________. Уровень В (конструктивный). 1. Найдите значения х, при которых р(х)=0, если р(х)=(2х+4)(х2 +3) А) -2;б) 2;в) -2; - 2. Найдите область определения функции у= а) (- 3. Разложите на множители квадратный трехчлен х2 -8х-9 а) (х-1)(х+9);б) (х+1)(х-9);в) (х-1)(х-9). 4. Для параболы, которая является графиком функции у=-2х2 +12х-19, определите координаты вершины а) (3;-1);б) (-3;1);в) (3;1). 5. При каких значениях х значения функции у=-х2 -2х+8 положительны? а) (- 6. Решите неравенство а) (- 7. Найдите значение Р, при которых уравнение 3х2 +Рх+3=0 имеет два корня а) (- 8. В арифметической прогрессии а3 =6 и d=1,2. Найдите сумму первых семи членов а) 50,4;б) 42,6;в) 54. 9. Найдите знаменатель q геометрической прогрессии (аn ), в которой а2 =3, а4 =0,75 а) 0,5;б) -0,5;в) 0,5 или -0,5. 10. Представьте в виде обыкновенной дроби число 0,(5) а) Уровень С (творческий). 1. Упростите выражение 2. Решите уравнение (х2 -3х)2 -2(х2 -3х)=8. 3. Найдите количество отрицательных членов арифметической прогрессии: -9,6; -8,3 … 4. Среди решений данного уравнения найдите те, которые удовлетворяют данному неравенству: 5. Из пункта А в пункт В выехал автобус и одновременно с ним из В в А выехал автомобиль. Они встретились в пункте С, причем расстояние, пройденное автомобилем до места встречи, оказалось на 50 км больше пройденного автобусом. Автобус прибыл в конечный пункт через 3 часа после встречи, а автомобиль – через 1 час 20 минут. На каком расстоянии от пункта А произошла встреча? За какое время автомобиль прошел все расстояние? 2 вариант. Уровень А (репродуктивный). Заполните пробелы: 1. Функция называется убывающей в некотором промежутке, если ______________________ значению аргумента из этого промежутка соответствует __________________________________________; 2. Квадратичной функцией называется функция, которую можно задать формулой _______________, где х-переменная, а, b и с - _______________________________________________, причем а≠0; 3. Геометрической прогрессией называют _____________________________, каждый член которой, _______________________________ равен предыдущему члену, ____________________________________; 4. Записать формулу n-го члена геометрической прогрессии и формулу суммы n первых членов геометрической прогрессии; 5. Функция y=f(x) называется нечетной, если область ее определения ____________________________ и для любого значения аргумента х верно равенство ___________________________. Уровень В (конструктивный). 1. Найдите значения х, при которых g(х)=0, если g(х)=(3х-9)(х2 +5) А) 3;б) -3;в) 3; - 2. Найдите область определения функции у= а) (- 3. Разложите на множители квадратный трехчлен 3х2 +17х-6 а) 3(х- 4. Для параболы, которая является графиком функции у=х2 -4х+7, определите координаты вершины а) (-2; 17);б) (2; 3);в) (2; -3). 5. При каких значениях х значения функции у=-х2 -3х+4 отрицательны? а) (-1; 4);б) (-4; 1);в) (- 6. Решите неравенство а) (- 7. Найдите значение Р, при которых уравнение 9х2 +Рх+1=0 имеет два корня а) (-6; 6);б) (- 8. В арифметической прогрессии а4 =-3 и d=-0,8. Найдите сумму первых восьми членов арифметической прогрессии а) -27,2;б) -28,6;в) -8,6. 9. Найдите знаменатель q геометрической прогрессии (аn ), в которой а1 =162, а3 =18 а) 3;б) -3;в) 3 или -3. 10. Представьте в виде обыкновенной дроби число 0,(15) а) Уровень С (творческий). 1. Упростите выражение 2. Решите уравнение (2х2 -х+1)2 -2(2х2 -х+1)+1=0. 3. Найдите количество положительных членов арифметической прогрессии: 14; 13,2 … 4. Среди решений данного уравнения найдите те, которые удовлетворяют неравенству: 5. Два трактора разной мощности, работая одновременно, вспахали поле за 2 часа 40 мин. Если бы первый трактор увеличил скорость вспашки в 2 раза, а второй – в 1,5 раза, то поле было бы вспахано за 1 ч 36 мин. За какое время вспахал бы поле первый трактор, работая с первоначальной скоростью? Уровень требований - высокий. 1 вариант. Уровень А (репродуктивный). 1. Записать определение функции, возрастающей на множестве х. 2. Запишите определение арифметической прогрессии, формулу n-го члена арифметической прогрессии, формулу суммы n первых членов арифметической прогрессии. 3. Дайте определение корня n-ой степени. 4. Дайте определение синуса угла. 5. Запишите основное тригонометрическое тождество. Уровень В (конструктивный). 1. Найдите корни квадратного трехчлена х2 -8х+23. 2. Решите неравенство х2 +х-6<0/ 3. Решите неравенство методом интервалов (х-3)(х-8)2 (х-10)>0. 4. Решите уравнение 5. Решите систему 6. найдите сумму первых десяти членов арифметической прогрессии 15,4; 13,8; 12,2; … 7. В геометрической прогрессии (bn ) найти S6 , если b1 =256, q=1/4. 8. Вычислите 9. Найдите значение выражения 10. Найдите значение tgα(ctgα +cosα), если sinα=-0,3. Уровень С (творческий). 1. Постройте график функции у= 2. Представьте выражение в виде степени с основанием а: 3. Упростить выражение 4. Найдите первый положительный член арифметической прогрессии -10,8; -10,2; -9,6;… 5. Решите уравнение х3 +2х2 +2х+1=0. 2 вариант. Уровень А (репродуктивный). 1. Записать определение функции, убывающей на множестве х. 2. Запишите определение геометрической прогрессии, формулу n-го члена геометрической прогрессии, формулу суммы n первых членов геометрической прогрессии. 3. Дайте определение степени с дробным показателем. 4. Дайте определение косинуса угла. 5. Запишите знаки тригонометрических функций в координатных четвертях. Уровень В (конструктивный). 1. Найдите корни квадратного трехчлена х2 -5х-24. 2. Решите неравенство х2 -х-20≥0. 3. Решите неравенство методом интервалов (х+10)2 (х+6)(х-7)≤0. 4. Решите уравнение 5. Решите систему 6. Найдите сумму первых десяти членов арифметической прогрессии 12,6; 11,1; 9,6; … 7. В геометрической прогрессии (bn ) найти S4 , если b1 =2, q=-3. 8. Вычислите 9. Найдите значение выражения 10. Найдите значение ctgα(tgα +sinα), если cosα=-0,2. Уровень С (творческий). 11. Постройте график функции у= 12. Представьте выражение в виде степени с основанием а: 13. Упростить выражение 14. Найдите первый положительный член арифметической прогрессии 10,1; 9,9; 9,7;… 15. Решите уравнение х3 +11х2 +11х+1=0. Контрольная работа по алгебре: 10 класс, нулевой срез, 2004-2005 учебный год.Учитель высшей категории М.Ю.Симатова Вариант 1. Уровень А (репродуктивный) 1. Найдите значение выражения А. 2. Чему равно произведение (1,6 × 10–8 )×(4 × 104 )? А. 0,064 Б. 0,000064 В. 0,00064 Г. 640 3. Из формулы пути равноускоренного движения А. t
= 4. Стоимость a карандашей равна х р. Сколько стоят b таких же карандашей? А. a
х
b
Б. 5. Укажите выражение, тождественно равное многочлену 6a – 8ab . А. –2a (3 – 4b ) Б. –2a (3 + 4b ) В. –2a (4b – 3) Г. –2a (–3 – 4b ) Уровень В (конструктивный). 1. Выполните действие: А. 2. Решите уравнение 10 – 7х = 3 – 2(5х + 1). А. –2,25 Б. –5,5 В. –3 Г. 6 3. В цирке перед началом представления было продано А. 40 Б. 80 В. 120 Г. 160 4. Найдите корни уравнения 32 – 2х 2 = 0. Ответ : __________________________ 5. На координатной прямой отмечены числа a , b и c . Какое из приведенных утверждений об этих числах неверно?
А. ab < 0 Б. b – c < 0 В. b + a > 0 Г. abc < 0 6.На каком рисунке изображено решение неравенства 2х + 3 > 6х – 5? А. В. Б. Г. 7.Последовательности заданы формулой n –ого члена. У какой из них каждый следующий член меньше предыдущего? А. an
= 2×10n
Б. an
= 2×(–10)n
В. an
= Уровень С (творческий). 1. Упростите выражение: 2.Найдите область определения функции у
= 3.На каждого жителя города Челябинска ежесуточно выбрасывается 3,5 кг вредных веществ. Какое количество вредных веществ в год выбрасывается на всех жителей города Челябинска, если сейчас в нём проживает 1,2 миллиона человек? Результат представить в стандартном виде. Спрогнозируйте ситуацию на 10 лет. 4.Решите систему уравнений: Вариант 2. Уровень А (репродуктивный) 1. Найдите значение выражения А. 2. Чему равно произведение (1,2× 10–8 )×(3 × 104 )? А. 0,036 Б. 0,000036 В. 0,00036 Г. 360 3. Из формулы пути равноускоренного движения А. t
= 4. Стоимость a карандашей равна у р. Сколько стоят b таких же карандашей? А. a
у
b
Б. 5. Укажите выражение, тождественно равное многочлену 4a2 -8ab. А. –4a(a– 4b ) Б. –4a (a + 4b ) В. –4a (2b – a) Г. –4a (a – 2b ) Уровень В (конструктивный). 1. Выполните действие: А. 2. Решите уравнение 10 – 3х = 5 – 2(3х - 1). А. –1,25 Б. –5,5 В. –1Г. 6 3. В цирке перед началом представления было продано А. 40 Б. 240 В. 24 Г. 160 4.Найдите корни уравнения 64 – 4х 2 = 0. Ответ : __________________________ 5.На координатной прямой отмечены числа a , b и c . Какое из приведенных утверждений об этих числах неверно?
А. ab < 0 Б. b – c < 0 В. b + a < 0 Г. abc > 0 6.На каком рисунке изображено решение неравенства 2х + 3 ³ 6х – 5?
А. В. Б. Г. 7.Последовательности заданы формулой n –ого члена. У какой из них каждый следующий член меньше предыдущего? А. an
= 5×10n
Б. an
= 5×(–10)n
В. an
= Уровень С (творческий). 1. Упростите выражение: 2. Найдите область определения функции у
= 3. На каждого жителя города Магнитогорска ежесуточно выбрасывается 5 кг вредных веществ. Какое количество вредных веществ в год выбрасывается на всех жителей города Челябинска, если сейчас в нём проживает 0,8 миллиона человек? Результат представить в стандартном виде. Спрогнозируйте ситуацию на 10 лет. 4. Решите систему уравнений: Контрольная работа по алгебре: 10 класс, промежуточный срез, 2004-2005 учебный год.Учитель высшей категории М.Ю.Симатова 1 вариант. Уровень А (репродуктивный). 1. На каком из рисунков изображен график показательной функции:
А) Б) В) 2. Укажите область определения у = 3х . а) (- 3. На каком из рисунков изображен график функции у=х-2 :
а)б)в) 4. Вычислить log5 125: a) 5;б) 3;в) 2;г) 25. 5. Найдите значение выражения 5log 5 25 : а) 5;б) 25;в) 2;г) 1. Уровень В (конструктивный). 6. Решить уравнение 4х-1 =1: а) 0;б) 1;в) 2;г) 4. 7. Решить уравнение: а) 8;б) 10;в) 2;г) 4. 8. Решить неравенство: а) [11;+ 9. Решить уравнение 32х-1 +32х =108: а) 2;б) 1,5;в) 27;г) 4. 10. Решить неравенство а) (- 11. Решить неравенство 9х -3х -6>0; а) (1; + 12. Решить уравнение log а) 5;б) 2;в) Ѕ;г) 4. 13. Вычислить 14. Вычислить 15. Вычислить log36 2-1/2log1/6 3. Ответ: ______________. Уровень С (творческий). Решить уравнение: 16. 2х+4
+2х+2
=5х+1
+3 18. Решить неравенство 19. Упростить выражение 20. При различных значениях а решить неравенство 2 вариант. Уровень А (репродуктивный). 1. На каком из рисунков изображен график степенной функции при p=2n:
А) Б) В) 2. Укажите область определения у = х1/2 . а) (- 3. На каком из рисунков изображен график функции у=х-5 :
а)б)в) 4. Вычислить log5 125: a) 5;б) 3;в) 2;г) 25. 5. Найдите значение выражения 2log 2 5 : а) 5;б) 25;в) 2;г) 1. Уровень В (конструктивный). 6. Решить уравнение 2х+1 =1: а) 0;б) 1;в) -1;г) 2. 7. Решить уравнение: а) 26;б) 9;в) 24;г) 11. 8. Решить неравенство: а) [21;+ 9. Решить уравнение 2х-1 +2х =192: а) 2;б) 5;в) 63;г) 4. 10. Решить неравенство а) (- 11. Решить неравенство 4х -2х -2>0; а) (1; + 12. Решить уравнение а) 33,5;б) 39;в) 30Ѕ;г) 40. 13. Вычислить 14. Вычислить 15. Вычислить 2log25 30+log0,2 6. Ответ: ______________. Уровень С (творческий). Решить уравнение: 16. 18. Решить неравенство 19. Упростить выражение 20. При различных значениях а решить неравенство Контрольная работа по алгебре: 10 профильный класс, итоговый срез, 2004-2005 учебный год.Учитель высшей категории Т.А.Шевченко 1 вариант. Уровень А (репродуктивный). 1. На тригонометрическом круге покажите расположение чисел а) arcsin 2) Запишите формулы корней уравнений и укажите область их применения (множество значений входящих в них букв) а) sin x=a;б) cos x=1. 3. Выясните, является ли функция четной, нечетной или не обладает этими свойствами y=- 4. Запишите с помощью формул правило для вычисления производной функции в точке х0 . 5.Функция у=f(x) задана графиком. Укажите: а) критические точки функции;б) точки экстремумов;в) точки области определения, где производная функции не определена. Уровень В (конструктивный) . 1. Найдите производную функции у=(2х-3)2 . 2. Решите уравнение х3 +6х2 +3х-10=0. 3. Решите неравенство sin 2x<0,5. 4. Найдите область определения функции у= 5. Упростите выражение 6. вычислите tg(arcsin 7. Написать уравнение наклонной асимптоты при х→ + 8. Функция у=f(x) определена на промежутке (а; 6). График ее производной изображен на рисунке. Укажите точку максимума функции у=f(x). 9. Решите уравнение 10. Найдите значение выражения Уровень С (творческий). 1. Решите уравнение 5tgx+cos2 x+sin 2x=1. 2. Найдите множество значений функции у=2sinx+ 3. Вычислите предел 4. Решите уравнение касательной к графику функции у= f(x)=6х2 -х-4, проходящего через точку М(0; -100). 5. В прямоугольном параллелепипеде две грани с общим ребром покрасили в голубой цвет, а остальные грани – в белый. Площадь белых граней равна 504, а одна из голубых граней – квадрат. Найдите наименьшее значение суммы длин всех ребер параллелепипеда, не являющихся ребрами голубых граней. 2 вариант. Уровень А (репродуктивный). 1. На тригонометрическом круге покажите расположение чисел а) arccos (- 2) Запишите формулы корней уравнений и укажите область их применения (множество значений входящих в них букв) а) cos x=a;б) sin x=0. 3. Выясните, является ли функция четной, нечетной или не обладает этими свойствами y= 4. Запишите с помощью формул правило для вычисления производной частного двух функций. 5.Функция у=f(x) задана графиком. Укажите: а) критические точки функции;б) точки экстремумов;в) точки области определения, где производная функции не определена. Уровень В (конструктивный). 1. Найдите производную функции у= 2. Решите уравнение х3 +4х2 -7х-10=0. 3. Решите неравенство cos 3x>0,5. 4. Найдите область определения функции у= 5. Упростите выражение 6. Вычислите tg(arccos 7. Написать уравнение наклонной асимптоты при х→ + 8. Функция у=f(x) определена на промежутке (а; 6). График ее производной изображен на рисунке. Укажите длину промежутка возрастания функции у=f(x). 9. Решите уравнение 10. Найдите значение выражения Уровень С (творческий). 1. Решите уравнение 12сtgx-2sin 2x=1+cos 2x. 2. Найдите множество значений функции у=2 3. Вычислите предел 4. Решите уравнение касательной к графику функции у= f(x)=7х2 -2х-5, проходящего через точку М(2; -93). 5. На графике функции f(x)=х2 -2 найдите точку, ближайшую к точке А(0,5; -0,75). 3 вариант. Уровень А (репродуктивный). 1. На тригонометрическом круге покажите расположение чисел а) arctg 1,5;б) arccos (-0,7). 2) Запишите формулы корней уравнений и укажите область их применения (множество значений входящих в них букв) а) tg x=a;б) cos x =1. 3. Выясните, является ли функция четной, нечетной или не обладает этими свойствами y= 4. Запишите с помощью формул правило для вычисления производной произведения двух функций. 5.Функция у=f(x) задана графиком. Укажите: а) критические точки функции;б) точки экстремумов;в) точки области определения, где производная функции не определена. Уровень В (конструктивный). 1. Найдите производную функции у=(1+sinx)2 . 2. Решите уравнение х3 -6х2 +3х+10=0. 3. Решите неравенство tg 4. Найдите область определения функции у= 5. Упростите выражение 6. Вычислите сtg(arcsin 0,8). 7. Написать уравнение наклонной асимптоты при х→ + 8. Функция у=f(x) определена на промежутке (а; 6). График ее производной изображен на рисунке. Укажите точку минимума функции у=f(x). 9. Решите уравнение 10. Найдите значение выражения Уровень С (творческий). 1. Решите уравнение sin 2x +1= sin2 x+6ctgx. 2. Найдите множество значений функции у=3sinx- 2cosx + 1. 3. Вычислите предел 4. Решите уравнение касательной к графику функции у= f(x)=4х2 -8х-2, проходящего через точку М(3; -90). 5. В прямоугольном параллелепипеде две грани с общим ребром покрасили в фиолетовый цвет, а остальные грани – в белый. Площадь белых граней равна 1080. белые грани, имеющие по два общих ребра с фиолетовыми гранями, являются квадратами. Найдите наименьшее значение суммы длин всех ребер параллелепипеда, исключая общее ребро фиолетовых ранней. Контрольная работа по алгебре: 11 класс, нулевой срез, 2004-2005 учебный год.Учитель высшей категории И.Г. Сазыкина. I вариант. Уровень А (репродуктивный) 3+х 1. Решите неравенство ------------ ≤ 0 (х+9)(х-1) 1) (-∞;-3]3) (-∞;-9) 2) [-3;1)U(9;+∞)4) (-∞;-3]U(1;9) 2. Решите уравнение sinx - √3/2=0
3. Укажите промежуток, которому принадлежит корень уравнения 34х+9 =27 1) (1;3)2) [-1;0]3) [-3;-1]4) (0;1] 4. Какому промежутку принадлежит корень уравнения log4 х =log4 7+log4 3? 1) (8;12)2) (24;28)3) (18;22)4) (2;6) 5. Вычислите 7-3•641/6 1) 12) 83) –54) -17 Уровень В (конструктивный). 5 √а11 1. Упростите выражение----- 5 √а 1) а12/5 2) а5 3) а2 4) а11/5 2. На каком из следующих рисунков функция, заданная графиком, возрастает на промежутке [-2;1]?
3. Какое из следующих чисел входит в множество значений функции у=(1/8)х -2? 1) –12) –23) –34) –6. 4. Укажите область определения функции у=4 √1-23х+9 1) [–3;+∞)2) (-∞;-3]3) (-3/5;-1/3]4) [–1/3;+∞) Уровень С (творческий). 1. Сколько корней имеет уравнение (sin4 x-cos4 x)log2 (1-x2 )=0? 2. Сплав алюминия и магния отличается большой прочностью и пластичностью. Взяли два таких сплава, сплавили их и получили сплав, содержащий 4% магния. Отношение масс первого и второго сплавов равно 3:2. Определите процент содержания магния во втором сплаве, если первый сплав содержит 6% магния. 3. Решите систему уравнений
II вариант. Уровень А (репродуктивный). (х-8)(х+5) 1. Решите неравенство ------------ ≥ 0 4+х 1) [8;+∞)3) (-∞;-5]U(-4;8] 2) [-5;+∞)4) [-5;-4)U[8;+∞) 2. Решите уравнение cosx - 1/2=0
3. Укажите промежуток, которому принадлежит корень уравнения 26х+7 =32 1) (1;3)2) (-3;-1]3) (-1;0)4) (0;1] 4. Какому промежутку принадлежит корень уравнения log5 х =log5 6+log5 3? 1) (17;21)2) (6;10)3) (13;17)4) (2;6) 5. Вычислите 3•125⅓ - 0,3 1) 142) 14,73) 15,34) 15 Уровень В (конструктивный). 5 √а11 1. Упростите выражение----- 5 √а 1) а12/5 2) а5 3) а2 4) а11/5 2. На каком из следующих рисунков функция, заданная графиком, убывает на промежутке [3;7]?
3. Какое из следующих чисел входит в множество значений функции у=11Х +11? 1) 12) 113) 124) 10 4. Укажите область определения функции у=8 √1-0,255х-8 1) [0;+∞)2) (-3;+∞)3) [1,6;+∞)4) [0,625;+∞) Уровень С (творческий). 1. Сколько корней имеет уравнение (sin4 x-cos4 x)log2 (1-x2 )=0? 2. Из двух сплавов, содержащих алюминий и магний, получили 4 кг нового сплава, в котором содержится 5% магния. Масса первого сплава, в котором 4% магния, в 4 раза меньше массы второго сплава. Сколько граммов магния содержалось во втором сплаве? 3. Решите систему уравнений
Таблица 6. Контроль знаний и умений учащихся по математике.
Таблица 7. Результаты тестовой формы контроля (нулевой и промежуточный срезы).
Выводы: Учащиеся с работой справились хорошо, показав достаточно высокий результат остаточных знаний и умений в классах 11в , 9б , 9а , 10а , учителя Сазыкина И.Г., Федорова Н.В., Шевченко Т.А. Подобрать систему заданий для учащихся, допустивших типичные ошибки при выполнении контрольной работы. Таблица 8.
Выводы: Учащиеся достаточно хорошо усвоили основные понятия и термины, особенно в классах с более высоким уровнем подготовки (9г, 10 а, в, г), поэтому первая часть работы тестовое задание выполнили практически все. Задание части В вызвало больше затруднений, так как требует хорошее знание алгоритмов и умение делать выводы. Наибольший интерес вызвало тестовое задание. В целом с работой справились все учащиеся. Много ошибок было сделано по темам: нахождение части от числа, действия с числами с разными знаками, свойства степеней, свойства неравенств, нахождение области определения функции, сопоставление графика с функцией. Следовательно, необходимо обратить внимание на данные темы в ходе повторения. Работа, составленная по трем этапам заданий, позволяет более глубоко оценить усвоенные знания учащихся и выявить пробелы. Таблица 9. Результаты итоговой контрольной работы.
Выводы: Все экспериментальные классы справились с контрольной работой. Высокие результаты показали 10г класс (учитель Симатова М.Ю.). Задание части В вызвало больше затруднений, так как требует хорошее знание алгоритмов и умение делать выводы. К заданиям части С многие учащиеся не приступили, т.к. оно требует умения использовать алгоритмы, но и уметь переносить знания из одной области в другую, выполнять анализ данных. В ходе повторения необходимо подобрать систему заданий учащимся, допустившим типичные ошибки при выполнении контрольной работы. 1.2 Контроль и оценка знаний и умений учащихся по информатики Учитель 1 категории Т.Ю.Ерёмина Классы: 10 Б, 10 В (химико-биологический), 10 Г (гуманитарный), 10 Д, 10 Е. Таблица 10. Структура учебной нагрузки
3. Формы контроля знаний, умений и навыков экспериментальных классов Таблица 11
Знания и умения учащихся по уровням требований по информатике. Таблица 12.
Контрольная работа по информатике: 10 класс, итоговый срез, 2004-2005 учебный год. Учитель 1 категории Т.Ю. Еремина Часть А. 1. За минимальную единицу измерения количества информации принят… 1) 1 бод2) 1 пиксель3) 1 байт4) 1 бит 2. Основной микросхемой, управляющей работой всех блоков компьютера и производящей обработку информации, является… 1) регистр2) процессор3) контроллер4) адаптер 3. Файл – это … 1) единица измерения информации; 2) программа или данные на диске, имеющие имя; 3) программа в оперативной памяти; 4) текст, распечатанный на принтере. 4. В растровом графическом редакторе изображение формируется из … 1) линий; 2) окружностей; 3) прямоугольников; 4) пикселей. 5. Гипертекст – это… 1) очень большой текст; 2) текст, в котором могут осуществляться переходы по выделенным ссылкам; 3) текст, набранный на компьютере; 4) текст, в котором используется шрифт большого размера. Часть В. 6. В барабане для розыгрыша лотереи находится 64 шара, причем среди них нет шаров с одинаковыми номерами. Сколько информации несет сообщение, что из барабана достали шар с номером 21? 1) 1 бит2) 8 байт3) 6 бит4) 21 бит 7. Для записи фрагмента текста из 80 символов использовался алфавит, который состоит из 32 букв. Какой объем информации содержит такой фрагмент текста? 1) 400 бит2) 32 бита3) 80 бит4) 8 байт 8. Черно-белое (без градаций серого) растровое графическое изображение имеет размер 10х10 точек. Какой объем памяти займет это изображение? 1) 100 бит2) 100 байт3) 10Кбайт4) 1000бит 9. Как записывается десятичное число 1210 в двоичной системе счисления? 1) 11112) 11003) 10114) 1001 10. Файл с именем r _ w . exe находится на логическом диске D , в каталоге TRANSFER , в подкаталоге WORK . Путем доступа к файлу r _ w . exe является … 1) TRANSFER\r_w.exe; 2) D:\TRANSFER\WORK\r_w.exe; 3) D:\r_w.exe; 4) D:\WORK\r_w.exe; 11. Для приведенного ниже абзаца текста выберите номер варианта, в котором правильно указаны использованные при наборе элементы форматирования…
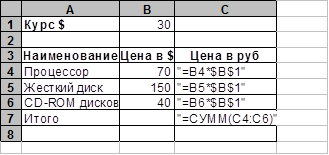
12. Какой вид примет содержащая абсолютную и относительную ссылку формула, записанная в ячейке С1, после ее копирования в ячейку С2?
1) =$A$1*B23) =$A$2*B1 2) =$A$1*B14) =$A$2*B2 13. Какой результат будет вычислен в ячейке С2 после копирования в нее формулы из ячейки С1, которая содержит абсолютную и относительную ссылку?
1) 03) 50 2) 254) 75 14. Какова таблица истинности логической функции F=A&B? 1)
2)
3)
4)
Часть С. 16. Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержат 5 страниц текста? 17. 256-цветный рисунок содержит 120 байт информации. Из скольких точек он состоит? 18. Сложить числа 11012 и 810 . Сумму представить в двоичной системе счисления. 9. По данным электронной таблицы построена диаграмма. Укажите имя столбца таблицы, данные которого отражены на диаграмме?
Средний уровень Часть А. 1. Чему равен 1 байт? 1) 8 бит2) 210 бит3) 10 бит4) 103 бит 2. Где должна находиться программа, команды которой в текущий момент выполняет процессор? 1) в оперативной памяти; 2) на жестком диске; 3) на устройстве ввода; 4) в постоянном запоминающем устройстве. 3. Операционная система – это … 1) программа, обеспечивающая управление базами данных; 2) антивирусная программа; 3) программа, управляющая работой компьютера; 4) система программирования. 4. В растровом графическом редакторе минимальным объектом, цвет которого можно изменить, является… 1) точка экрана (пиксель); 2) графический примитив (точка, линия, окружность и т.д.) 3) знакоместо (символ); 4) выделенная область. 5. Абзацем в текстовом редакторе является… 1) фрагмент документа между двумя маркерами абзаца; 2) выделенный фрагмент документа; 3) строка символов; 4) фрагмент документа, начинающийся с отступа (красной строки). Часть В. 6. Какое количество информации получит второй игрок при игре в крестики-нолики на поле 8х8, после первого хода первого игрока, играющего крестиками? 1) 4 бита2) 5 бит3) 6 бит4) 7 бит 7. Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, с помощью которого было записано это сообщение? 1) 4 символа2) 16 символов3) 32 символа4) 8 символов 8. Цветное (с палитрой из 256 цветов) растровое графическое изображение имеет размер 10х10 точек. Какой объем памяти займет это изображение? 1) 100 бит2) 400 бит3) 800 бит4) 10 байт 9. Как записывается восьмеричное число 678 в десятичной системе счисления? 1) 532) 543) 554) 56 10. Файловую систему обычно изображают в виде дерева, где «ветки» - это каталоги (папки), а «листья» - это файлы (документы). Что может располагаться непосредственно в корневом каталоге, т.е. на «стволе» дерева? 1) каталоги и файлы;3) только файлы; 2) только каталоги;4) ничего 11. Для приведенного ниже абзаца текста использовались элементы форматирования…
1) отрицательный выступ, выравнивание по левому краю, шрифт с засечками, обычное и полужирное начертание; 2) красная строка, выравнивание по левому краю, шрифт с засечками, обычное и полужирное начертание; 3) красная строка, выравнивание по ширине, шрифт рубленый, полужирное и курсивное начертание; 4) выравнивание по центру, шрифт с засечками, полужирное начертание 12. В результате использования функции в ячейке D1 появилось число, равное 9. В ячейке D1 записана функция…
1) СЧЁТ2) МАКС3) СУММ4) СРЗНАЧ 13.В электронных таблицах в столбцах А и В хранятся данные, а в столбец С введены формулы. Какие значения будут храниться в ячейках столбца С ?
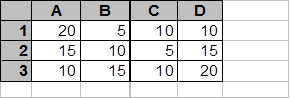
1) 0 и 12) 1 и 13) 0 и 04) 1 и 0 14. Какова таблица истинности логической функции F=AvB? 1)
2)
3)
4)
1) A2) B3) B4) A Часть С. 16. Система оптического распознавания символов позволяет преобразовывать отсканированные изображения страниц документа в текстовый формат со скоростью 4 страницы в минуту и использует алфавит мощностью 65536 символов. Какое количество информации будет нести текстовый документ после 5 минут работы приложения, страницы которого содержат 40 строк по 50 символов? 17. Для хранения изображения размером 64х32 точек выделено 64Кбайт памяти. Определите, какое максимальное число цветов допустимо использовать в этом случае. 18. Вычислить арифметическое выражение: 32Е16 -1111012 +2078 . Результат выражения записать в десятичной системе счисления. 19. По данным электронной таблицы построен график. Укажите имя столбца таблицы, данные которого отражены на графике?
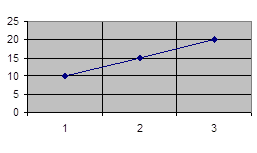
Высокий уровень Часть А. 1. Чему равен 1Мбайт? 1) 106 бит2) 106 байт3) 1024 Кбайт4) 1024байт 2. Процессор обрабатывает информацию… 1) в десятичной системе счисления; 2) на языке программирования высокого уровня; 3) на алгоритмическом языке; 4) на машинном языке (в двоичном коде). 3. В процессе загрузки операционной системы происходит… 1) копирование файлов операционной системы с гибкого диска на жесткий диск; 2) копирование файлов операционной системы с CD-ROM на жесткий диск; 3) последовательная загрузка файлов операционной системы в оперативную память; 4) копирование содержимого оперативной памяти на жесткий диск. 4. Векторные графические изображения хорошо поддаются масштабированию (изменению размеров), так как… 1) используют большую глубину цвета; 2) формируются из пикселей; 3) формируются из графических примитивов (линий, окружностей, прямоугольников и т.д.) 4) используют эффективные алгоритмы сжатия. 5. Какой универсальный (доступный для различных текстовых редакторов) формат текстовых файлов полностью сохраняет форматирование документа? 1) HTM2) RTF3) DOC4) TXT Часть В. 6. В школьной библиотеке 16 стеллажей с книгами. На каждом стеллаже 8 полок. Библиотекарь сообщил ученику, что нужная ему книга находится на пятом стеллаже на третьей сверху полке. Какое количество информации библиотекарь передал ученику. 1) 4 бита2) 5 бит3) 6 бит4) 7 бит 7. Во сколько раз уменьшится информационный объем страницы текста при его преобразовании из кодировки Unicode (таблица кодировки содержит 65536 символов) в кодировку WindowsCP1251 (таблица кодировки содержит 256 символов)? 1) в 256 раз2) в 8 раз3) в 4 раза4) в 2 раза 8. Для кодирования черно-белого полутонового изображения размером 64х32 точек использовались 16 уровней серого. Какой объем памяти потребуется для хранения такого изображения, если каждой точке изображения соответствует один из 16 уровней серого? 1) 32 Кбайта2) 16 Кбайт3) 1 Кбайт4) 4 Кбайта 9. Укажите, какое число из предложенных будет соответствовать числу 1А16 1) 110112 2) 2910 3) 328 4) 111002 10. Системная дискета необходима для: 1) первоначальной загрузки операционной системы; 2) систематизации файлов; 3) хранения важных файлов; 4) лечения компьютера от вирусов. 11. Выберите последовательность операций форматирования, которые были применены к исходному фрагменту теста:
1) Выделить строку, Установить полужирный шрифт, Выравнивание по центру, выравнивание по левому краю; 2) Выделить фрагмент текста, Удалить, Выделить строку, Установить полужирный шрифт; 3) Выделить строку, Установить полужирный шрифт, Выравнивание по центру, Выделить строку, Установить подчеркнутый шрифт; 4) Выделить фрагмент текста, Удалить, Выделить строку, Изменить размер шрифта. 12. В электронных таблицах хранятся данные, а в столбец С введены формулы. Какие значения будут храниться в ячейках столбца С ?
1) 702) 21003) 2104) 100 150 4500 450 180 40 1200 120 70 260 7800 780 350 13. В электронных таблицах хранится база данных о процессорах. В каком порядке расположатся записи с данными после их сортировки по возрастанию по текстовому столбцу С ?
1) Запись 22) Запись 43) Запись 14) Запись 1 Запись 3 Запись 3 Запись 2 Запись 4 Запись 4 Запись 2 Запись 3 Запись 2 Запись 1 Запись 1 Запись 4 Запись 3 14. Какова таблица истинности логической функции F=A&B? 1)
2)
3)
4)
1) A2) B3) B4) A Часть С. 16. Определить длительность звукового файла, который уместится на гибкой дискете 3,5’. Для хранения данных на такой дискете выделяется 2847 секторов объемом 512 байт. а) при низком качестве звука: моно, 8 бит, 8КГц; б) при высоком качестве звука: стерео, 16 бит, 48КГц. 17. Используются графические режимы с глубинами цвета 8, 16, 24 и 32 бита. Вычислить объемы видеопамяти, необходимые для реализации данных глубин цвета при разрешающей способности экрана 800х600. 18. Заполнить таблицу:
19. Представлен фрагмент электронной таблицы и график, построенный после удаления одной из строк таблицы. Укажите номер удаленной строки.
20. Составить таблицу истинности для формулы XvYvX&Z. Защита проекта. Учащиеся должны продемонстрировать умения и навыки по созданию мультимедийной компьютерной презентации:- выбор дизайна презентации из коллекции или создание фона; - вставка различных объектов в презентацию (рисунки, графические примитивы, таблицы, графики и т.д.); - создание анимации в презентации; - настройка переходов между слайдами, а также создание управляющих кнопок; - и, конечно, содержание презентации. Таблица 13 Критерии оценивания презентаций учащихся.
Таблица 14 Итоги защиты проекта
Таблица 15
Итоговый тест Таблица 16
Таблица 17
Таблица18. Результаты защиты проекта
Таблица 19 Результаты итоговой работы
Выводы: Учащиеся справились с работой хорошо. Причем при выполнении контрольных срезов учащиеся показали стабильные знания. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 .
.
 .
.


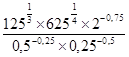 .
. .
.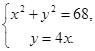
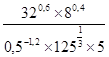 .
.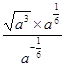 .
.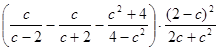 .
.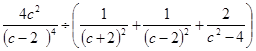 .
.

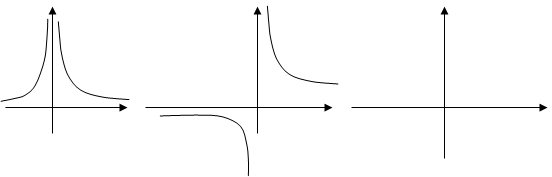
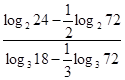 . Ответ: _______________.
. Ответ: _______________.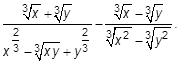
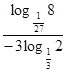 . Ответ: ___________.
. Ответ: ___________.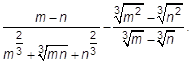
 .
.