Задача 11
. Найти производную.
11.1. 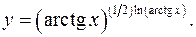
lny= 1/2*ln2
arctgx
y'= (arctgx)1/2*ln(arctgx)
(lnarctgx)/(arctgx*(1+x2
))
11.2. 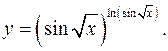
lny= ln2
sin√x
y'= ((sin√x)lnsin√x
*ctg√x*lnsin√x)/√x
11.3. 
lny= 5ex
lnsinx
y'= (sinx)5e^x
(5ex
lnsinx+5ex
ctgx)
11.4. 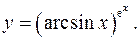
lny= ex
lnarcsinx
y'= (arcsinx)e^x
(ex
lnarcsinx+ex
/√(1-x2
))
11.5. 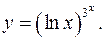
lny= 3x
lnlnx
y'= (lnx)3^x
(3x
ln3lnlnx+3x
/(xlnx))
11.6. 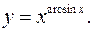
lny= arcsinxlnx
y'= xarcsinx
(lnx/√(1-x2
)+arcsinx/x)
11.7. 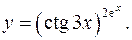
lny= 2ex
lnctg3x
y'= 2(ctg3x)2e^x
(ex
lnctg3x-3ex
/(ctg3x*sin2
3x))
11.8. 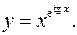
lny= etgx
lnx
y'= xe^tgx
((etgx
lnx)/cos2
x+etgx
/x)
11.9. 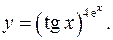
lny= 4exlntgx
y'= (tgx)4e^x
(4ex
lntgx+ 4ex
) = (tgx)4e^x
(4ex
lntgx+ 4ex
) =
tgxcos2
x sinxcosx
11.10. 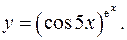
lny=exlncos5x
y'= (cos5x)e^x
(ex
lnco5x-5ex
sin5x
)= ex
(cos5x)e^x
(lncos5x-5tg5x)
cos5x
11.11. 
lny= 8ln2
(xsinx)
y'= 16(xsinx)8ln(xsinx)
ln(xsinx)(sinx+xcosx)
11.12. 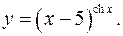
lny= chxln(x-5)
y'= (x-5)chx
(shxln(x-5)+chx/(x-5))
11.13. 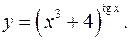
lny= tgxln(x3+4)
y'= (x3
+4)tgx
(ln(x3
+4)/cos2
x+(3x2
tgx)/(x3
+4))
11.14. 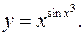
lny= sinx3
lnx
y'= xsinx^3
(3x2
cosx3
lnx+(sinx3
)/x)
11.15. 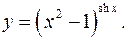
lny= shxln(x2
-1)
y'= (x2
-1)shx
(chxln(x2
-1)+(2xshx)/(x2
-1))
11.16. 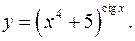
lny= ctgxln(x4+5)
y'= (x4
+5)ctgx
(-(ln(x4
+5))/sin2
x+(4x3
ctgx)/(x4
+5))
11.17. 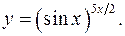
lny= 5x/2*lnsinx
y'= (sinx)5x/2
(2,5lnsinx+(5xcosx)/sinx)= (sinx)5x/2
(2,5lnsinx+5xctgx)
11.18. 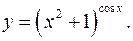
lny= cosxln(x2+1)
y'= (x2
+1)cosx
(-sinxln(x2
+1)+(2xcosx)/(x2
+1))
11.19. 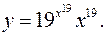
lny= x19
ln19+19lnx
y'= 19x^19
x19
(19x18
ln19+19/x)
11.20. 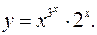
lny= 3x
lnx+xln2
y'= x3^x
2x
(3x
ln3lnx+3x
/x+ln2)
11.21. 
lny= e1/x
lnsin√x
y'= (sin√x)e^1/x
(-(e1/x
lnsin√x)/x2
+(e1/x
cos√x)/(2√xsin√x))=
= e1/x
(sin√x)e^1/x
((ctg√x)/(2√x)-(lnsin√x)/x2
)
11.22. 
lny= ectgx
lnx
y'= xe^ctgx
(-(ectgx
lnx)/sin2
x+ectgx
/x)= ectgx
xe^ctgx
(1/x-(lnx)/sin2
x)
11.23. 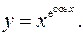
lny= ecosx
lnx
y'= xe^cosx
(-ecosx
sinxlnx+ecosx
/x)= ecosx
xe^cosx
(1/x-sinxlnx)
11.24. 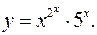
11.25. 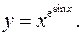
lny= esinx
lnx
y'= xe^sinx
(esinx
cosxlnx+esinx
/x)= ecosx
xe^cosx
(cosxlnx+1/x)
11.26. 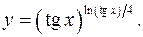
lny= ln2
(tgx)/4
y'= (tgx)ln(tgx)/4
/*(ln(tgx))/(2cos2
x)
11.27. 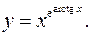
lny= earctgx
lnx
y'= xe^arctgx
((earctgx
lnx)/(1+x2
)+ earctgx
/x)
11.28. 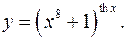
lny= thxln(x8
+1)
y'= (x8
+1)thx
((ln(x8
+1))/ch2
x+(8x7
thx)/(x8
+1))
11.29. 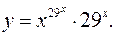
lny= 29x
lnx+xln29
y'= x29^x
29x
(29x
ln29lnx+29x
/x+ln29)
11.30. 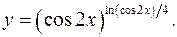
lny= ln2
(cos2x)/4
y'= (cos2x)ln(cos2x)/4
(-ln(cos2x)sin2x)/cos2x
11.31. 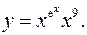
lny= ex
lnx+9lnx
y'= xe^x
x9
(ex
lnx+ex
/x+9/x)
|