СОДЕРЖАНИЕ
| ВВЕДЕНИЕ………………………………………………………………... |
3 |
| ГЛАВА 1. Эконометрические модели .……………………………....….. |
5 |
| 1.1 Основные понятия и особенности эконометрических моделей …………………………………………………………. |
5 |
| 1.2 Структурная и приведенная формы моделей …………….. |
7 |
| 1.3 Проблема идентификации……………………………...…... |
9 |
| 1.4 Оценивание параметров структурной модели……………. |
10 |
| 1.4.1 КМНК………………………………………………....... |
11 |
| 1.4.2 ДМНК………………………………………………....... |
12 |
| 1.5 Большие эконометрические модели………………………. |
13 |
| 1.5.1 Математические основы больших эконометрических моделей…………………………………….................................. |
14 |
| 1.5.2. Исторические примеры больших эконометрических моделей………………………………………………………….. |
22 |
| ГЛАВА 2. Эконометрическая модель национальной экономики Турции …………………………………………………………………….. |
25 |
| 2.1 План работы …………………………………………….….. |
25 |
| 2.2 Идентификация модели…………………………………….. |
26 |
| 2.3 Прогнозирование эндогенных переменных………………. |
30 |
| 2.4 Выводы……………………………………………………… |
32 |
| ЗАКЛЮЧЕНИЕ…………………………………………………………… |
33 |
| СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………………… |
34 |
| ПРИЛОЖЕНИЯ…………………………………………………………… |
35 |
ВВЕДЕНИЕ
Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточны для описания таких систем и объяснения механизма их функционирования. При использовании отдельных уравнений регрессии, например, для экономических расчетов в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение одной переменной, как правило, не может происходить при абсолютной неизменности других. Ее изменение повлечет за собой изменения во всей системе взаимосвязанных признаков [4].
Следовательно, отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в экономических, биометрических социологических исследованиях важное место заняла проблема описания структуры связей между переменными системы так называемых одновременных уравнений или структурных уравнений.
Эконометрические методы применяются для построения крупных эконометрических систем моделей, описывающих экономику той или иной страны и включающих в качестве составных элементов производственную функцию, инвестиционную функцию, а также уравнения, характеризующие движение занятости, доходов, цен и процентных ставок и другие блоки.
Одним из традиционных подходов к исследованию макроэкономических процессов является подход, основанный на использовании эконометрических моделей.[11]
Эконометрические модели позволяют решать достаточно широкий круг задач исследования: анализ причинно-следственных связей между экономическими переменными; прогнозирование значений экономических переменных; построение и выбор вариантов (сценариев) экономической политики на основе имитационных экспериментов с моделью. Моделирование и прогнозирование макроэкономических процессов является, несомненно, актуальной проблемой экономики. [9]
В последние десятилетия методы эконометрики сыграли решающую роль в освоении и развитии автоматизации экономических расчетов разного уровня и назначения.
Цель курсовой работы – рассмотреть системы эконометрических уравнений (большие эконометрические модели), их применение в эконометрике.
Предмет работы – эконометрика как набор математическо-статистических методов.Объект работы – системы эконометрических уравнений.
В связи с поставленной целью, мной были выделены задачи данной курсовой работы:
· Понятие больших эконометрических моделей;
· Сущность проблемы идентифицируемости;
· Особенности системы линейных одновременных эконометрических уравнений;
· Методы наименьших квадратов;
· Применение эконометрических уравнений.
ГЛАВА 1. Эконометрические модели.
1.1
Основные понятия и особенности эконометрических моделей.
Эконометрическая модель — основное понятие эконометрии, экономико-математическая модель, параметры которой оцениваются с помощью методов математической статистики. Она выступает в качестве средства анализа и прогнозирования конкретных экономических процессов как на макро-, так и на микроэкономическом уровне на основе реальной статистической информации.
Наиболее распространены эконометрические модели, представляющие собой системырегрессионных уравнений, в которых отражается зависимость эндогенных величин (искомых) от внешних воздействий (текущих экзогенных величин) в условиях, описываемых параметрами модели, а также лаговыми переменными. Кроме регрессионных (как линейных, так и нелинейных) уравнений, применяются и другие математико-статистическиемодели.[2]
Эконометрическая модель может быть представлена в двух формах: структурной и приведенной.
Эконометрический метод включает решение следующих проблем:
· качественный анализ связей экономических переменных - выделение зависимых и независимых переменных;
· подбор данных;
· оценка параметров модели;
· проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты (гипотезы о средней, дисперсии и ковариации);
· анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, выявление переменных, ответственных за мультиколлинеарность;
· введение фиктивных переменных;
· выявление автокорреляции, лагов;
· выявление тренда, циклической и случайной компонент;
· проверка остатков на гетероскедастичность;
· анализ структуры связей и построение системы одновременных уравнений;
· проверка условия идентификации;
· оценивание параметров системы одновременных уравнений (двухшаговый и трехшаговый метод наименьших квадратов, метод максимального правдоподобия);
· моделирование на основе системы временных рядов: проблемы стационарности и коинтеграции;
· построение рекурсивных моделей, ARIMA- и VAR- моделей;
· проблемы идентификации и оценивания параметров.
Эконометрическая модель, как правило, основана на теоретическом предположении о круге взаимосвязанных переменных и характере связи между ними. При всем стремлении к «наилучшему» описанию связей приоритет отдается качественному анализу.[3]
Поэтому в качестве этапов эконометрического исследования можно указать:
· постановку проблемы;
· получение данных, анализ их качества;
· спецификацию модели;
· оценку параметров;
· интерпретацию результатов.
Этот список менее подробен, чем предыдущий, и включает те стадии, которые проходит любое исследование, независимо от того, на использование каких данных оно ориентировано: пространственных или временных.[3]
1.2 Структурная и приведенная формы моделей
 Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях - в правую часть системы: Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях - в правую часть системы:
y1
= b12
y2
+ b13
y3
+… + b1n
yn
+ a11
x1
+ a12
x2
+…+ a1m
xm
+ e1
,
y2
= b21
y1
+ b23
y3
+… + b2n
yn
+ a21
x1
+ a22
x2
+…+ a2m
xm
+ e2
,
…………………………………………………………………,
yn
= bn1
y1
+ bn2
y2
+… + bnn-1
yn-1
+ an1
x1
+ an2
x2
+…+ anm
xm
+ en
.
Система взаимозависимых уравнений получила название система совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные у одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от других систем каждое уравнение системы одновременных уравнений не может рассматриваться самостоятельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.[4]
Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.
 Простейшая структурная форма модели имеет вид: Простейшая структурная форма модели имеет вид:
y1
= b12
y2
+ a11
x1
+ e1
,
y2
= b21
y1
+ a22
x2
+ e2
.
Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.
Структурная форма модели в правой части содержит при эндогенных и экзогенных переменных коэффициенты bi
и aj
(bi
— коэффициент при эндогенной переменной, aj
- коэффициент при экзогенной переменной), которые называются структурные коэффициенты модели. Все переменные в модели выражены в отклонениях от среднего уровня, т. е. под х подразумевается x — хср
, а под у — соответственно у —yср
. Поэтому свободный член в каждом уравнении системы отсутствует.
Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.
Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:
 y1
= δ11
x1
+ δ12
x2
+ … + δ1m
xn
, y1
= δ11
x1
+ δ12
x2
+ … + δ1m
xn
,
y2
= δ11
x1
+ δ12
x2
+ … + δ1
m
xn
,
………………………………..,
yn
= δn
1
x1
+ δn
2
x2
+ … + δnm
xn
.
δij
– коэффициенты приведенной формы модели.
По виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным методом наименьших квадратов. Применяя МНК, можно оценить δ, а затем оценить значения эндогенных переменных через экзогенные.
Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели.[6]
1.3 Проблема идентификации.
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация – это единственность соответствия между приведенной и структурной формами модели.
С позиции идентификации структурные модели можно подразделить на три вида [5]:
· идентифицируемые;
· неидентифицируемые;
· сверхидентифицируемые.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной модели, т.е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели и модель идентифицируема.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов.[7]
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверить на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неидентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы.
Чтобы уравнение было идентифицируемо, необходимо, чтобы число экзогенных переменных (D), отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении (H) без одного.
D+1=H – уравнение идентифицируемо;
D+1<H – уравнение неидентифицируемо;
D+1>H – уравнение сверхидентифицируемо.
Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, определитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.[6]
Целесообразность проверки условия идентификации модели через определитель матрицы, коэффициентов, отсутствующих в данном уравнении, но присутствующих в других уравнениях, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие идентификации.
1.4 Оценивание параметров структурной модели.
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:
• косвенный метод наименьших квадратов (КМНК);
• двухшаговый метод наименьших квадратов (ДМНК);
• трехшаговый метод наименьших квадратов (ТМНК);
• метод максимального правдоподобия с полной информацией (ММПf
);
• метод максимального правдоподобия при ограниченной информации (ММПs
).
Косвенный и двухшаговый методы наименьших квадратов подробно описаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели. Эти методы достаточно легкореализуемы. Косвенный метод наименьших квадратов применяется для идентифицируемой системы одновременных уравнений, а двухшаговый метод наименьших квадратов - для оценки коэффициентов сверхидентифицируемой модели. Перечисленные методы оценивания также используются для сверхидентифицируемых систем уравнений.[5]
Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации. В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой.[6]
1.4.1 КМНК.
Как уже отмечалось, косвенный метод наименьших квадратов используется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы:
· структурная модель преобразовывается в приведенную форму модели;
· для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты (δij
);
· для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты (δij
);
· коэффициенты приведенной формы модели трансформируются в параметры структурной модели.
При сравнении результатов, полученных традиционным методом наименьших квадратов и с помощью косвенного метода наименьших квадратов, следует иметь в виду, что традиционный МНК, применяемый к каждому уравнению структурной формы модели, взятому в отдельности, дает смещенные оценки структурных коэффициентов.
1.4.2 ДМНК.
Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут применяться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов.
Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название «двухшаговый метод наименьших квадратов», ибо МНК используется дважды: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной ŷi
= δi
1
x1
+ δi
2
x2
+ … + δij
xj
и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.
Свёрхидентифицируемая структурная модель может быть двух типов:
· все уравнения системы сверхидентифицируемы;
· система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.
Если все уравнения системы сверхидентйфицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Двухшаговый метод наименьших квадратов является наиболее общим и широко распространенным методом решения системы одновременных уравнений. [6]
1.5 Большие эконометрические модели.
Большие эконометрические модели (LSEM) — это комплексная система эконометрических уравнений для описания мировой экономики или экономики конкретного региона. Подобная система может включать сотни, а то и тысячи уравнений. Конечно же, нет человека, который был бы способен решать такие модели, хотя необходимые расчеты можно выполнить с помощью компьютера. Тем не менее по своей базовой структуре такие модели очень похожи на изученные нами. Сложности возникают при неочевидном нарушении связей между потреблением, инвестициями, спросом на деньги и т.д. LSEM применяется в моделировании в основном для ответа на вопрос: какое количественное воздействие оказывают на эндогенные переменные (выпуск, цены и пр.) изменения экзогенных переменных (например, фискальной, денежной политики, обменного курса).[8]
1.5.1 Математические основы больших эконометрических моделей.
Основной областью применения эконометрических моделей
является построение макроэкономических моделей экономики целой страны. Это, главным образом, мультипликаторные модели кейнсианского типа
. Более совершенными по сравнению со статическими моделями являются динамические модели
экономики, которые содержат в правой части лаговые переменные
и учитывают тенденцию развития (фактор времени). Значительные трудности создает невыполнение условия независимости факторов, которое в корне нарушается в системах одновременных (взаимозависимых) уравнений [1].
Отметим, что наличие множества прикладных моделей для решения одного и того же класса задач не случайно. Наиболее ярко это проявляется при построении макроэкономических моделей, когда, например, одна и та же функция потребления может включать в себя разный набор экономических переменных.
Рассмотрим основные направления практического использования эконометрических систем уравнений (больших эконометрических моделей).
Наиболее широко системы одновременных уравнений применяются для построения макроэкономических моделей функционирования экономики той или иной страны. Большинство из них представляют собой мультипликаторные модели кейнсианского типа с той или иной степенью сложности. Статическая модель Кейнса для описания народного хозяйства страны в наиболее простом варианте имеет следующий вид:
 C = a + by + e, C = a + by + e,
Y = C + I,
где С — личное потребление в постоянных ценах;
у - национальный доход в постоянных ценах;
е - случайная составляющая;
I - инвестиции в постоянных ценах.
В силу наличия тождества в модели (второе уравнение системы) структурный коэффициент bне может быть больше 1. Он характеризует предельную склонность к потреблению. Так, если b = 0,65, то из каждой дополнительной 1 тыс. руб. дохода на потребление расходуется в среднем 650 руб. и 350руб. инвестируется т. е. С и у выражены в тысячах рублей. Если b > 1 , то у < C + 1, т. е. на потребление расходуются не только доходы, но и сбережения. Параметр а Кейнс истолковывал как прирост потребления за счет других факторов. Поскольку прирост во времени может быть не только положительным, но и отрицательным (снижение), такой вывод возможен. Однако суждение о том, что параметр а характеризует конкретный уровень потребления, обусловленный влиянием других факторов, неправильно.[6]
Структурный коэффициент bиспользуется для расчета мультипликаторов. По данной функции потребления можно определить два мультипликатора - инвестиционный мультипликатор потребления Мс
и инвестиционный мультипликатор национального дохода Му
.
Инвестиционный мультипликатор потребления рассчитывается по формуле
Mc
= b/ (1-b)
Инвестиционный мультипликатор национального дохода можно определить как
Му
= 1 / (1 — b),
Рассматриваемая модель Кейнса точно идентифицируема, и для получения величины структурного коэффициента bприменяется КМНК, т.е. строится система приведенных уравнений.
Таким образом, приведенная форма модели содержит мультипликаторы, интерпретируемые как коэффициенты линейной регрессии, отвечающие на вопрос, на сколько единиц изменится значение эндогенной переменной, если экзогенная переменная изменится на одну единицу своего измерения. Этот смысл коэффициентов приведенной формы делает приведенную модель удобной для прогнозирования.
В более поздних исследованиях статическая модель Кейнса включала уже не только функцию Потребления, но и функцию сбережений:
 C = a + by + e1
, C = a + by + e1
,
r = T + K(C + I) + e2
,
y = C +I + r,
где С, y и I – те же по смыслу переменные, что и в предыдущей модели;
r - сбережения.
Данная модель содержит три эндогенные переменные — С, г, у и одну экзогенную переменную I.Система идентифицируема: в первом уравнении Н = 2 и в =1, во втором H=1 и в = 0;С + I рассматривается как предопределенная переменная.
 Наряду со статическими широкое распространение получили динамические модели экономики. В отличие от статических они содержат в правой части лаговые переменные, а также учитывают тенденцию (фактор времени). Например, модели Клейна, разработанные им для экономики США в 1950-1960 гг. В упрощенном варианте модель Клейна рассматривается как конъюнктурная модель. Наряду со статическими широкое распространение получили динамические модели экономики. В отличие от статических они содержат в правой части лаговые переменные, а также учитывают тенденцию (фактор времени). Например, модели Клейна, разработанные им для экономики США в 1950-1960 гг. В упрощенном варианте модель Клейна рассматривается как конъюнктурная модель.
Ct
= b1
St
+ b2
Pt
+ b3
+ e1
,
It
= b4
Pt
+ b5
Pt-1
+ b6
+e2
,
St
= b7
Rt
+ b8
Rt-1
+ b9
t + b10
+ e3
,
Rt
= St
+ Pt
+ Tt
,
Rt
= Ct
+ It
+ Gt
,
где Ct
- функция потребления в период t;
St
- заработная плата в период t;
Pt
- прибыль в период t;
Pt
-1
- прибыль в период t - 1, т. е. в предыдущий год;
Rt
- общий доход в период t;
Rt
-1
- общий доход в предыдущий период;
t - время;
Tt
- чистые трансферты в пользу администрации в период t;
It
- капиталовложения в период t,
Gt
- спрос административного аппарата, правительственные расходы в период времени t.
Модель содержит пять эндогенных переменных - Ct
,It
,St
,
Rt
(расположены в левой части системы) и Pt
(последняя — зависимая переменная, определяемая по первому тождеству), три экзогенные переменные - Tt
,Gt
t и две предопределенных, лаговых переменных - Pt
-1
и Rt
-1 .
Как и большинство моделей такого типа, данная модель сверхидентифицируема и решаема ДМНК. Для прогнозных целей используется приведенная форма модели
 Ct
= d1
T + d2
G + d3
t + d4
Pt-1
+ d5
Rt-1
+u1
, Ct
= d1
T + d2
G + d3
t + d4
Pt-1
+ d5
Rt-1
+u1
,
It
= d6
T + d7
G + d8
t + d9
Pt-1
+ d10
Rt-1
+u2
,
St
= d11
T + d12
G + d13
t + d14
Pt-1
+ d15
Rt-1
+u3
,
Rt
= d16
T + d17
G + d18
t + d19
Pt-1
+ d20
Rt-1
+u4
,
Pt
= d21
T + d22
G + d23
t + d24
Pt-1
+ d25
Rt-1
+u5
.
В этой системе мультипликаторами являются коэффициенты при обычных экзогенных переменных. Они отражают влияние экзогенной переменной на эндогенную переменную. Мультипликаторами в нашей системе выступают коэффициенты при Т и С. Коэффициенты d1,
d6,
d11,
d16,
d21
- мультипликаторы чистых трансфертов в пользу администрации относительно личного потребления d1
, инвестиций d6
, заработной платы d11
, дохода d16
и прибыли d21.
Соответственно коэффициенты d2,
d7,
d12,
d17,
d22
являются мультипликаторами правительственных расходов относительно соответствующих эндогенных переменных.[6]
Динамическая модель может и не содержать учет тенденции, но лаговые переменные в ней обязательны. Динамическая модель Кейнса представлена следующими тремя уравнениями:
 Ct
= a + b1
Y1
+ b2
Yt
-1
+e1
, Ct
= a + b1
Y1
+ b2
Yt
-1
+e1
,
Yt
= Ct
+ Gt
+ It
+ Lt
,
Pt
= Yt
+ Zt
.
Yt
, -- имеющийся в распоряжении доход в период времени t;
Ct
, -- частное потребление в период времени t;
Pt
-- валовой национальный продукт (ВНП) в период времени t.
Кроме того, модель содержит пять предопределенных переменных: Yt
-1
- доход предыдущего года;
Ct
, -- частное потребление;
It
- валовые капиталовложения;
Lt
- изменение складских запасов;
Zt
- сальдо платежного баланса.
Случайная переменная e1
характеризует ошибки в первом уравнении ввиду его статистического характера. Параметр а отражает влияние других не учитываемых в данном уравнении факторов потребления (например, цен). Первое уравнение данной системы является сверхидентифицируемым, а второе и третье — определениями.
Если в модели Кейнса доход рассматривается как лаговая переменная, то в других исследованиях функции потребления в виде лаговой переменной используется потребление предыдущего года, т. е. считается, что потребление текущего года зависит не только от дохода, но и от достигнутого в предыдущий период уровня потребления.
 Примером динамической модели экономики, учитывающей для каждой эндогенной переменной лаговые переменные соответствующего экономического содержания, может служить модель открытой экономики с экономической активностью со стороны государства. Примером динамической модели экономики, учитывающей для каждой эндогенной переменной лаговые переменные соответствующего экономического содержания, может служить модель открытой экономики с экономической активностью со стороны государства.
Ct
= a0
+ a1
Yt
+ a2
Ct-1
+e1
,
It
= b0
+ b1
Yt
+ b2
Ut-1
+ e2
,
IMt
= k0
+ k1
Yt
+ k2
IMt-1
+ e3
,
Yt
= Ct
+ It
+ Gt
– IMt
.
В этой модели четыре эндогенные переменные:
Ct
— личное потребление в период времени t;
It
— частные чистые инвестиции в отрасли экономики в период времени t;
IMt
—импорт в период времени t;
Yt
— национальный доход за период времени t.
Все переменные приведены в постоянных ценах.
Предопределенными переменными в модели являются следующие три переменные:
Ct
-1
— личное потребление за предыдущий период;
Ut
-1
— доход личных домохозяйств от предпринимательской деятельности за предыдущий период и доход от имущества плюс нераспределенная прибыль предприятий до налогообложения;
IMt
-1
— импорт за предыдущий период времени t-1.
В качестве экзогенной переменной в модели рассматривается переменная Gt
— общественное потребление плюс государственные чистые капиталовложения в экономику страны плюс изменение запасов минус косвенные налоги плюс, дотации плюс экспорт.
Первые три уравнения системы являются сверхидентифицируемыми, а четвертое представляет собой балансовое тождество.
 Система одновременных уравнений нашла применение в исследованиях спроса и предложения. Линейная модель спроса и предложения имеет вид: Система одновременных уравнений нашла применение в исследованиях спроса и предложения. Линейная модель спроса и предложения имеет вид:
Qd
= a0
+ a1
P + e1
,
Qs
= b0
+ b1
P +e2
,
Qd
= Qs
,
где Qd
— спрашиваемое количество благ (объем спроса);
Р - цена;
Qs
- предлагаемое количество благ (объем предложения).
В этой системе три эндогенные переменные Qd
, Qs
и P. При этом если Qd
и Qs
представляют собой эндогенные переменные исходя из структуры самой системы (они расположены в левой части), то Р является эндогенной по экономическому содержанию (цена зависит от предлагаемого и испрашиваемого количества благ), а также в результате наличия тождества Qd
= Qs
.
Рассматриваемая модель спроса и предложения не содержит экзогенной переменной. Однако для того, чтобы модель имела статистическое решение и можно было убедиться в ее справедливости, в модель вводятся экзогенные переменные.
 Одним из вариантов модели спроса и предложения является модель вида Одним из вариантов модели спроса и предложения является модель вида
Qd
= a0
+ a1
P + a2
R + e1
,
Qs
= b0
+ b1
P + b2W + e2,
Qd
= Qs
,
где R - доход на душу населения;
W — климатические условия (предположим, что речь идет о спросе и предложении зерна).
Переменные Rи W экзогенные. Введя их в модель, получим идентифицируемую структурную модель, оценки параметров которой могут быть даны с помощью КМНК.
Широкий класс моделей в эконометрике представляют производственные функции:
Р =f ( x1
,x2
,..,xn
), где
Р — объем выпуска (уровень производства);
x1
,x2
,..,xn
- факторы производства (труд, капитал и др.).
Однако реализация такого рода моделей, как правило, не связана с системой одновременных уравнений. Производственная функция в упрощенном виде может быть включена в систему одновременных уравнений. Так, в 1962 г. Б. Хохенбалкен и Г. Тинтнер предложили следующую модель экономики для каждой из одиннадцати стран — членов Организации экономического содружества:
logX = a2
+ b2
logD,
dx/dD = W/p,
Y =C + K,
X = Y/P.
Здесь эндогенными переменными являются:
С - величина личного потребления в текущих ценах;
Y- ВНП в текущих ценах;
X- ВНП в постоянных ценах;
Р - индекс цен;
D — общая занятость.
В качестве экзогенных переменных приняты:
N— численность населения;
W- средняя годовая заработная плата работника;
K — государственное потребление плюс инвестиции и внешнеторговое сальдо.
В системе имеются только два структурных уравнения -функция потребления (первое уравнение) и производственная функция (второе уравнение). Остальные составляющие модели представляют собой априорно разработанную функцию спроса на труд (третье уравнение) и два тождества, относящиеся к ВНП.
Параметры функции потребления оцениваются с помощью КМНК с учетом тождества Y= С + К, а параметры производственной функции — при комбинации ее с функцией спроса на труд.
Как уже отмечалось, не все эконометрические модели имеют вид системы одновременных уравнений. Так, широкий класс функций спроса на ряд потребительских товаров часто представляет собой рекурсивную систему, в которой с уравнениями можно работать последовательно и проблемы одновременного оценивания не возникают. В этом плане система одновременных уравнений — лишь один из возможных вариантов построения экономических моделей.[6]
1.5.2. Исторические примеры больших эконометрических моделей.
Первой версией модели LSEM в международном масштабе был Проект LINK, созданный Л.Клейном и его ассистентами из Пенсильванского университета в конце 60-х годов. LINK состоит из 79 субмоделей, каждая из которых описывает страну или отдельный географический регион, а все вместе они охватывают весь мир. В свою очередь, каждая субмодель является широкомасштабной моделью.
Проект LINK, вероятно, наиболее широко известен, но это только одна из моделей подобного рода. Перечислим несколько других подобных моделей, которые были разработаны государственными агентствами во всем мире: ЕРА — мировая эконометрическая модель, созданная Японским агентством экономического планирования, содержащая модели для восьми стран: Австралии, Канады, Франции, Италии, Японии, Великобритании, Соединенных Штатов и Западной Германии, и шесть моделей для остальных регионов мира; EEC — модель Европейской экономической комиссии, содержащая четыре субмодели: для Соединенных Штатов, Японии, Европы и остального мира; MINIMOD — сравнительно небольшая модель Международного валютного фонда, состоящая , всего из двух субмоделей: для США и остальных стран, входящих в Организацию экономического сотрудничества и развития (ОЭСР), созданная совместными усилиями Ричарда Хааса и Пола Массона.
Широкомасштабные модели были также разработаны частными фирмами, которые занимались экономическими консультациями и прогнозами. В числе этих моделей можно отметить: DRI — модель объединенных данных о ресурсах, включающая субмодели для Канады, Японии, Соединенных Штатов и региональную модель для Европы; наконец, WHARTON — модель Вартоновской эконометрической ассоциации прогнозов, включающая 23 субмодели для каждой из стран ОЭСР, одну для Южной Африки и шесть региональных моделей для остальных стран мира. Наконец, ученые из университетов разработали собственные модели. Например, модель MSG — глобальная модель Мак-Кибина—Сакса, разработанная Варвиком Мак-Кибином и Джеффри Саксом из Гарвардского университета. Она состоит из пяти субмоделей, представляющих Японию, США, блок стран ОЭСР, страны ОПЕК и другие развивающиеся страны.
Недавно Ральф Брайант, Джон Хелливелл и Питер Хупер смоделировали различные виды экономической политики в США, основываясь на хорошо известных моделях LSEM. Эти модели обеспечивают возможность получения "усредненных" результатов, нивелируя тем самым крайности частных моделей. Основываясь на модели IS-LM, можно предсказать сокращение выпуска, цен и процентной ставки. Брайант, Хелливелл и Хупер смоделировали ежегодное сокращение государственных расходов на 1% ВВП в течение 6 лет. В соответствии с этим за первый год выпуск упал немногим более чем на 1%, во втором году несколько увеличился, не достигнув, однако, первоначального уровня. Цены в первом году снизились незначительно (менее чем на 0,1%), а краткосрочная ставка процента упала на 1,09.
Другим политическим решением, рассмотренным авторами, было увеличение предложения денег в США на 1% в течение 6 лет. Теоретическая модель предсказывает понижение процентных ставок, рост выпуска и цен. В имитационной модели ставки процента в США действительно сильно упали в первом году и постепенно увеличивались в дальнейшем. Выпуск увеличился на 0,25% в первом году, еще немного во втором, а затем начал падать, возвращаясь к исходному уровню.[8]
Таким образом, количественные результаты, полученные на базе данной теоретической модели, совпадают с результатами, которые дают большие эконометрические модели. Конечно же, реальный мир очень сложен, и это многообразие может быть отражено только большими, а не простыми эконометрическими моделями. Например, мы не можем точно учесть результаты многообразных видов политики и лагов. Но ведь главное требование к простой модели — отражать наиболее важные аспекты действительности и давать реальные прогнозы. Модель IS-LM в сочетании с моделью QS/QP удовлетворяет этим требованиям для многих случаев краткосрочных изменений в политике.[8]
Глава 2.
Эконометрическая модель национальной экономики Турции.
2.1 План работы.
План работы следующий:
1. Собрать исходные данные в виде временных рядов с 1970 года по 2007 год следующих макроэкономических показателей: валовой внутренний продукт, непроизводственное потребление, государственные расходы, инвестиции.
2. Идентифицировать по косвенному или двухшаговому методу наименьших квадратов, следующую экономическую модель:

где c1
– склонность к потреблению, i1
– склонность к инвестированию.
3. Осуществить по модели прогноз на 2008,2009,2010гг. эндогенных показателей Ct
, It
, Yt
, используя при этом прогноз по тренду экзогенного показателя Gt
.
4. Описать результаты указанных выше работ.
2.2 Идентификация модели
.
Для составления эконометрической модели национальной экономики Турции идентифицируем следующую эконометрическую модель:
 , ,
, где
,
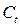 - потребление за год - потребление за год 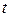 , ,
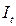 - инвестиции за год - инвестиции за год 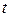 , ,
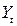 - ВВП за год - ВВП за год 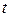 (без чистого экспорта и прироста запасов), (без чистого экспорта и прироста запасов),
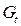 - государственные расходы за год - государственные расходы за год 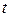 , ,
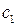 - склонность к потреблению, - склонность к потреблению,
 - склонность к инвестированию, - склонность к инвестированию,
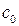 , , 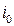 - свободные члены уравнения, - свободные члены уравнения,
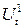 , ,  - случайные остатки уравнения. - случайные остатки уравнения.
В этой системе три эндогенных переменных  и одна экзогенная переменная и одна экзогенная переменная . .
Проверим модель на идентифицируемость:
Необходимое условие:
1-е уравнение:
H=2 (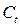 , ,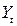 ) D=1( ) D=1(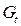 ) )
D+1=H => уравнение точно идентифицируемо
2-е уравнение:
H=2 (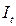 , ,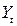 ) D=1( ) D=1(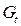 ) )
D+1=H => уравнение точно идентифицируемо
Достаточное условие:
1-е уравнение:
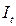 |
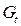 |
| 2 |
-1 |
0 |
| 3 |
1 |
1 |
det = -1 ≠ 0
rang = 2
Число эндогенных переменных равно 3 , 3-1=2, т.е. ранг равен числу эндогенных переменных без одного => уравнение точно идентифицируемо. , 3-1=2, т.е. ранг равен числу эндогенных переменных без одного => уравнение точно идентифицируемо.
2-е уравнение:
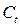 |
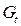 |
| 1 |
-1 |
0 |
| 3 |
1 |
1 |
det = -1 ≠ 0
rang = 2
Число эндогенных переменных равно 3 , 3-1=2, т.е. ранг равен числу эндогенных переменных без одного => уравнение точно идентифицируемо. , 3-1=2, т.е. ранг равен числу эндогенных переменных без одного => уравнение точно идентифицируемо.
Из необходимого и достаточного условий следует, что система точноидентифицируема, применяется КМНК (косвенный метод наименьших квадратов).
Идентификация модели состоит в нахождении по исходным данным оценок коэффициентов модели c0
, с1
, i0
, i1
для структурной формы модели.
Приведем систему уравнение модели к структурному виду, в которой нет балансовых переменных. Подставим для этого балансовую переменную в остальные уравнения.
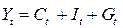 Исключим из системы уравнений (1) балансовое уравнение : Исключим из системы уравнений (1) балансовое уравнение :

, ,
. .

,
- структурная форма модели
.
 Разрешаем уравнение структурной формы (2) относительно эндогенных переменных Разрешаем уравнение структурной формы (2) относительно эндогенных переменных  и и 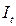 и получаем приведенную форму модели: и получаем приведенную форму модели:
,
. где

,
,
,
,
,
.
   Проведя вычисления с помощью программы Excel, используя МНК (см. таблицы № 2,3 Приложения), получим следующие оценочные коэффициенты. Чтобы упростить процедуру расчетов будем работать с отклонениями от средних уровней, т.е. Сt
- Сt
, Gt
- Gt
, It
- It
. Проведя вычисления с помощью программы Excel, используя МНК (см. таблицы № 2,3 Приложения), получим следующие оценочные коэффициенты. Чтобы упростить процедуру расчетов будем работать с отклонениями от средних уровней, т.е. Сt
- Сt
, Gt
- Gt
, It
- It
.
 Система нормальных уравнений в общем виде : Система нормальных уравнений в общем виде :
∑y = na + b1
∑x1
+ b2
∑x2
+ … +bp
∑xp
,
∑yx1
= a∑ x1
+ b1
∑ (x1
)2
+ b2
∑x1
x2
+ … + bp
∑xp
x1
, (5)
……………………………………………………. ,
∑yxp
= a∑xp
+ b1
∑x1
xp
+ b2
∑x2
xp
+ … + bp
∑(xp
)2
.
 Из системы нормальных уравнений для каждого из уравнений следует, что: Из системы нормальных уравнений для каждого из уравнений следует, что:
(6)
Подставив найденные оценки 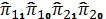 в систему (3), получим: в систему (3), получим:
Ĉ = 26209,95+5,77 , ,
Î = -2133,10+ 2,17 . .
Теперь найдем 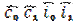 на основании системы (4): на основании системы (4):

  Подставим полученные коэффициенты в исходную модель (1): Подставим полученные коэффициенты в исходную модель (1):
2
2.3 Прогнозирование эндогенных переменных
.
Для прогноза эндогенных переменных на  шагов вперед (в моем случае на три шага) необходимо задать значения предопределенных переменных шагов вперед (в моем случае на три шага) необходимо задать значения предопределенных переменных 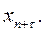 Предопределенная переменная в моей работе (в моем случае экзогенная) – Предопределенная переменная в моей работе (в моем случае экзогенная) –  (государственные расходы в год (государственные расходы в год 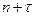 ). Поскольку у меня нет данных о будущих государственных расходах, то получим их путем прогноза по линейному тренду: ). Поскольку у меня нет данных о будущих государственных расходах, то получим их путем прогноза по линейному тренду:  . .
Для прогноза на 2008, 2009, 2010 года воспользуемся следующим уравнением:
 , где n – номер последнего года из Приложения №1 , где n – номер последнего года из Приложения №1
Найдем методом наименьших квадратов коэффициенты.
 ; ;  2486,29. 2486,29.
 ; ;  691,37. 691,37.
Уравнение регрессии примет следующий вид:
 где где  ; ;
Таким образом, получаем:
для прогноза на 2008 год, т.е. при  =1 , =1 ,
для прогноза на 2009 год, т.е. при  =2, =2,
для прогноза на 2010 год, т.е. при  =3. =3.
Затем осуществляем прогноз эндогенных показателей:
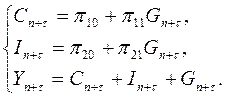
Находим прогноз будущих значений государственных расходов на 2008 г., 2009 г., 2010 г. ( и и  и и 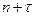 = 41 ). = 41 ).
Исходя из уравнения регрессии, находим:
G39
= 29449,71,
G40
= 30141,08,
G41
= 30832,45.
Подставив эти значения в формулы для выровненных значений эндогенных переменных, получим:
Прогноз на 2008 г.
C39
= 26209,95+5,77G39
= 196126,38
I39
= - 2133,1+2,17 G39
=61745,71
Y39
= 29449,71+196126+61746 =287321,81
Прогноз на 2009 г.
C40
= 26209,95+5,77G40
= 200115,39
I40
= - 2133,1+2,17 G40
=63245,35
Y40
= 29449,71+196126+61746 =293501,82
Прогноз на 2010 г.
C
41
= 26209,95+5,77G41
= 204104,40
I41
= - 2133,1+2,17 G41
=64744,99
Y41
= 29449,71+196126+61746 =299681,84
Сведем прогнозные оценки в таблицу :
| Год
|
G
|
C
|
I
|
Y
|
| 2008
|
29449,71 |
196126,38 |
61745,71 |
287321,81 |
| 2009
|
30141,08 |
200115,39 |
63245,35 |
293501,82 |
| 2010
|
30832,45 |
204104,40 |
64744,99 |
299681,84 |
2.4 Выводы
В ходе работы была проведена идентификация эконометрической модель национальной экономики Турции с помощью косвенного метода наименьших квадратов. На основе полученной модели, которая отражает взаимосвязь макроэкономических показателей (ВВП, непроизводственного потребления, инвестиций и государственных расходов) за 1970-2007гг, был сделан прогноз на 2008 г.,2009 г и 2010 г. Полученные данные позволяют сделать вывод о развитии экономики Турции.
В результате анализа данных за 1970-2007 гг. можно прийти к следующим выводам:
1) наблюдается стабильный рост по всем показателям;
2) высокими темпами растут ВВП, непроизводственное потребление, затем чистые инвестиции, государственные расходы, что свидетельствует о развитии экономики страны.
Что касается перспектив развития, то согласно составленному прогнозу объемы ВВП, инвестиций и непроизводственного потребления, гос. расходов значительно упадут в 2008 году. Потом эти показатели начнут постепенно увеличиваться в последующих годах. [11]
ЗАКЛЮЧЕНИЕ
Эконометрическая модель может представлять собой как очень сложную систему, так и простую формулу, которая может быть легко подсчитана на калькуляторе. В любом случае она требует знаний по экономике и статистике. Сначала для определения соответствующих взаимосвязей применяются знания по экономике, а затем для оценки количественной природы взаимосвязей полученные за прошедший период данные обрабатываются с помощью статистических методов.
Большие эконометрические модели насчитывают большое число уравнений, которые описывают большое число важных взаимосвязей. Преимущество больших эконометрических моделей состоит в том, что с их помощью существует возможность проводить расчеты по широкому спектру макроэкономических и отраслевых исследований. В качестве основных препятствий на пути дальнейшего развития системы моделей следует отметить традиционные трудности, связанные с качеством текущей экономической статистики. Тем не менее, представленный комплекс моделей нашел практическое использование как при разработке долгосрочного прогноза развития экономики страны, так и при проведении исследований в отдельных регионах.[1]
Проблема исследования больших эконометрических моделей носит актуальный характер в современных условиях. В настоящее время макроэкономическим вопросам развития страны посвящено множество различных работ, которые позволяют увидеть, насколько необходимы знания в области эконометрического моделирования, в частности, изучение и разработка больших эконометрических моделей.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник для вузов. - М.: ЮНИТИ, 1998. - 1022 с.
2. Колемаев В.А. Эконометрика, учебник – М.: Инфра М, 2005 г.
3. Орлов А.И. Эконометрика. Учебник. М.: Издательство "Экзамен", 2002.
4. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордиенко и др. - М.: Финансы и статистика, 2001. - 192 с.
5. Тихомиров Н.П., Дорохина Е.Ю. Эконометрика. – М.: Экзамен, 2003.
6. Эконометрика./Под ред. И.И. Елисеевой, - М.: Финансы и статистика, 2002.
7. Я.Р. Магнус, П.К.Катышев, А.А. Пересецкий. «Эконометрика начальный курс» М.: изд-во «Дело» 2000.
ИНТЕРНЕТ – РЕСУРСЫ:
8. Большие эконометрические модели (LSEM) [Электронный ресурс] // Режим доступа:meconomics.info/makroekonomicheskaya-politika-i-opredelenie-vypuska-v- zakrytoj-ekonomike.html (дата обращения 22.11.10).
9. В.И.Малюгин, М.В.Пранович, Д.Л.Мурин, Д.Л.Калечиц. Система эконометрических моделей для анализа, прогнозирования и оценки вариантов денежно-кредитной политики [Электронный ресурс] // Режим доступа: www.nbrb.by/publications/research/research_2.pdf (дата обращения 22.11.10).
10. Системы эконометрических уравнений, их применение в эконометрике [Электронный ресурс] // Режим доступа: studentbank.ru/view.php?id=67001 (дата обращения 22.11.10).
11. Эконометрическая модель национальной экономики Турции [Электронный ресурс] // Режим доступа: revolutionemodel/00171225.html (дата обращения 22.11.10).
ПРИЛОЖЕНИЯ
Таблица 1
Макроэкономические показатели Турции в сопоставимых ценах 1995 г. (в млн. долларах США)
| Год |
В сопоставимых ценах 1995 г. (млн. $) |
| ВВП |
Потребление |
Госрасходы |
Инвестиции |
| 1 |
2 |
3 |
4 |
5 |
| 1970 |
62352 |
51900 |
4671 |
10551,00 |
| 1971 |
65702 |
56475 |
4952 |
9695,00 |
| 1972 |
70911 |
60151 |
5316 |
11545,00 |
| 1973 |
73632 |
61293 |
5770 |
12494,00 |
| 1974 |
78406 |
57187 |
6250 |
18788,00 |
| 1975 |
84429 |
62578 |
7643 |
19610,00 |
| 1976 |
92942 |
68873 |
8862 |
23460,00 |
| 1977 |
97539 |
81393 |
9201 |
18397,00 |
| 1978 |
95032 |
82683 |
8938 |
15256,00 |
| 1979 |
94314 |
81615 |
8723 |
15676,00 |
| 1980 |
96477 |
84912 |
7110 |
13051,00 |
| 1981 |
99300 |
81322 |
10583 |
17179,00 |
| 1982 |
101132 |
85583 |
9460 |
16198,00 |
| 1983 |
106853 |
92011 |
11026 |
16617,00 |
| 1984 |
113841 |
98980 |
11236 |
16772,00 |
| 1985 |
117626 |
99557 |
12823 |
18694,00 |
| 1986 |
125814 |
105677 |
14008 |
20262,00 |
| 1987 |
137680 |
106320 |
15331 |
29404,00 |
| 1988 |
136612 |
107361 |
15167 |
29098,00 |
| 1989 |
138292 |
106454 |
15292 |
29738,00 |
| 1990 |
157127 |
119850 |
16516 |
34459,00 |
Продолжение таблицы 1
| 1 |
2 |
3 |
4 |
5 |
| 1991 |
156396 |
123204 |
17120 |
34608,00 |
| 1992 |
165951 |
127228 |
17742 |
36808,00 |
| 1993 |
187098 |
138152 |
19262 |
46509,00 |
| 1994 |
165566 |
130694 |
18196 |
39082,00 |
| 1995 |
183856 |
137279 |
19436 |
42655,00 |
| 1996 |
197291 |
148943 |
21105 |
48656,00 |
| 1997 |
214653 |
160795 |
21975 |
55875,00 |
| 1998 |
216868 |
162946 |
23700 |
53698,00 |
| 1999 |
208437 |
160235 |
25239 |
45277,00 |
| 2000 |
228301 |
170302 |
27041 |
52923,00 |
| 2001 |
190801 |
154788 |
24733 |
36229,00 |
| 2002 |
208178 |
158615 |
26069 |
35830,00 |
| 2003 |
226397 |
167451 |
25432 |
39408,00 |
| 2004 |
256057 |
182569 |
25567 |
52162,00 |
| 2005 |
277954 |
197403 |
26187 |
64693,00 |
| 2006 |
293741 |
208527 |
28704 |
73742,00 |
| 2007 |
306700 |
215643 |
30398 |
80007,00 |
Таблица 2
| Год |
 |
 |
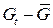 |
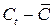 |
 |
 |
 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 1970 |
4671 |
51900 |
-11297 |
-66441 |
127622209 |
750581301 |
4414375009 |
| 1971 |
4952 |
56475 |
-11016 |
-61866 |
121352256 |
681513247 |
3827372651 |
| 1972 |
5316 |
60151 |
-10652 |
-58190 |
113465104 |
619837357 |
3386048536 |
| 1973 |
5770 |
61293 |
-10198 |
-57048 |
103999204 |
581773089 |
3254447281 |
| 1974 |
6250 |
57187 |
-9718 |
-61154 |
94439524 |
594292270 |
3739782748 |
| 1975 |
7643 |
62578 |
-8325 |
-55763 |
69305625 |
464225003 |
3109485755 |
Продолжение таблицы 2
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 1976 |
8862 |
68873 |
-7106 |
-49468 |
50495236 |
351517925 |
2447059592 |
| 1977 |
9201 |
81393 |
-6767 |
-36948 |
45792289 |
250025513 |
1365137202 |
| 1978 |
8938 |
82683 |
-7030 |
-35658 |
49420900 |
250674075 |
1271476073 |
| 1979 |
8723 |
81615 |
-7245 |
-36726 |
52490025 |
266078154 |
1348781680 |
| 1980 |
7110 |
84912 |
-8858 |
-33429 |
78464164 |
296111984 |
1117482206 |
| 1981 |
10583 |
81322 |
-5385 |
-37019 |
28998225 |
199346040 |
1370388826 |
| 1982 |
9460 |
85583 |
-6508 |
-32758 |
42354064 |
213187523 |
1073071047 |
| 1983 |
11026 |
92011 |
-4942 |
-26330 |
24423364 |
130121690 |
693256428 |
| 1984 |
11236 |
98980 |
-4732 |
-19361 |
22391824 |
91615131 |
374839150 |
| 1985 |
12823 |
99557 |
-3145 |
-18784 |
9891025 |
59074935 |
352829758 |
| 1986 |
14008 |
105677 |
-1960 |
-12664 |
3841600 |
24820976 |
160370897 |
| 1987 |
15331 |
106320 |
-637 |
-12021 |
405769 |
7657226 |
144498747 |
| 1988 |
15167 |
107361 |
-801 |
-10980 |
641601 |
8794790 |
120555199 |
| 1989 |
15292 |
106454 |
-676 |
-11887 |
456976 |
8035452 |
141295138 |
| 1990 |
16516 |
119850 |
548 |
1509 |
300304 |
827062 |
2277796 |
| 1991 |
17120 |
123204 |
1152 |
4863 |
1327104 |
5602449 |
23651073 |
| 1992 |
17742 |
127228 |
1774 |
8887 |
3147076 |
15765958 |
78982979 |
| 1993 |
19262 |
138152 |
3294 |
19811 |
10850436 |
65258214 |
392485105 |
| 1994 |
18196 |
130694 |
2228 |
12353 |
4963984 |
27523012 |
152602460 |
| 1995 |
19436 |
137279 |
3468 |
18938 |
12027024 |
65677805 |
358656815 |
| 1996 |
21105 |
148943 |
5137 |
30602 |
26388769 |
157203691 |
936496900 |
| 1997 |
21975 |
160795 |
6007 |
42454 |
36084049 |
255022601 |
1802362226 |
| 1998 |
23700 |
162946 |
7732 |
44605 |
59783824 |
344887691 |
1989627154 |
| 1999 |
25239 |
160235 |
9271 |
41894 |
85951441 |
388401470 |
1755127081 |
| 2000 |
27041 |
170302 |
11073 |
51961 |
122611329 |
575366776 |
2699970134 |
| 2001 |
24733 |
154788 |
8765 |
36447 |
76825225 |
319460031 |
1328401073 |
| 2002 |
26069 |
158615 |
10101 |
40274 |
102030201 |
406810066 |
1622014153 |
Продолжение таблицы 2
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 2003 |
25432 |
167451 |
9464 |
49110 |
89567296 |
464779281 |
2411815363 |
| 2004 |
25567 |
182569 |
9599 |
64228 |
92140801 |
616526845 |
4125266408 |
| 2005 |
26187 |
197403 |
10219 |
79062 |
104427961 |
807936998 |
6250837294 |
| 2006 |
28704 |
208527 |
12736 |
90186 |
162205696 |
1148611912 |
8133557316 |
| 2007 |
30398 |
215643 |
14430 |
97302 |
208224900 |
1404071278 |
9467725294 |
| Итого |
606784 |
4496949 |
0 |
0 |
2239108404 |
12919016822 |
77244410549 |
Таблица 3
| Год |
 |
 |
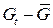 |
 |
 |
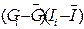 |
 |
| 1970 |
4671 |
10551 |
-11297 |
-21952 |
127622209 |
247989366 |
481881061 |
| 1971 |
4952 |
9695 |
-11016 |
-22808 |
121352256 |
251250609 |
520195261 |
| 1972 |
5316 |
11545 |
-10652 |
-20958 |
113465104 |
223242373 |
439228940 |
| 1973 |
5770 |
12494 |
-10198 |
-20009 |
103999204 |
204049635 |
400351656 |
| 1974 |
6250 |
18788 |
-9718 |
-13715 |
94439524 |
133280324 |
188095450 |
| 1975 |
7643 |
19610 |
-8325 |
-12893 |
69305625 |
107332472 |
166224020 |
| 1976 |
8862 |
23460 |
-7106 |
-9043 |
50495236 |
64258062 |
81772041 |
| 1977 |
9201 |
18397 |
-6767 |
-14106 |
45792289 |
95453877 |
198973297 |
| 1978 |
8938 |
15256 |
-7030 |
-17247 |
49420900 |
121244930 |
297451747 |
| 1979 |
8723 |
15676 |
-7245 |
-16827 |
52490025 |
121910090 |
283140844 |
| 1980 |
7110 |
13051 |
-8858 |
-19452 |
78464164 |
172303951 |
378372114 |
| 1981 |
10583 |
17179 |
-5385 |
-15324 |
28998225 |
82518606 |
234818524 |
| 1982 |
9460 |
16198 |
-6508 |
-16305 |
42354064 |
106111570 |
265846160 |
| 1983 |
11026 |
16617 |
-4942 |
-15886 |
24423364 |
78507572 |
252358307 |
| 1984 |
11236 |
16772 |
-4732 |
-15731 |
22391824 |
74438096 |
247457737 |
| 1985 |
12823 |
18694 |
-3145 |
-13809 |
9891025 |
43428643 |
190682667 |
| 1986 |
14008 |
20262 |
-1960 |
-12241 |
3841600 |
23991947 |
149836927 |
| 1987 |
15331 |
29404 |
-637 |
-3099 |
405769 |
1973929 |
9602496 |
Продолжение таблицы 3
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 1988 |
15167 |
29098 |
-801 |
-3405 |
641601 |
2727236 |
11592591 |
| 1989 |
15292 |
29738 |
-676 |
-2765 |
456976 |
1868998 |
7644061 |
| 1990 |
16516 |
34459 |
548 |
1956 |
300304 |
1072003 |
3826760 |
| 1991 |
17120 |
34608 |
1152 |
2105 |
1327104 |
2425203 |
4431911 |
| 1992 |
17742 |
36808 |
1774 |
4305 |
3147076 |
7637443 |
18534838 |
| 1993 |
19262 |
46509 |
3294 |
14006 |
10850436 |
46136457 |
196173933 |
| 1994 |
18196 |
39082 |
2228 |
6579 |
4963984 |
14658481 |
43286011 |
| 1995 |
19436 |
42655 |
3468 |
10152 |
12027024 |
35207866 |
103067379 |
| 1996 |
21105 |
48656 |
5137 |
16153 |
26388769 |
82979042 |
260926210 |
| 1997 |
21975 |
55875 |
6007 |
23372 |
36084049 |
140396869 |
546260225 |
| 1998 |
23700 |
53698 |
7732 |
21195 |
59783824 |
163881368 |
449236949 |
| 1999 |
25239 |
45277 |
9271 |
12774 |
85951441 |
118429706 |
163180455 |
| 2000 |
27041 |
52923 |
11073 |
20420 |
122611329 |
226112991 |
416984998 |
| 2001 |
24733 |
36229 |
8765 |
3726 |
76825225 |
32660235 |
13884645 |
| 2002 |
26069 |
35830 |
10101 |
3327 |
102030201 |
33608154 |
11070330 |
| 2003 |
25432 |
39408 |
9464 |
6905 |
89567296 |
65350912 |
47681932 |
| 2004 |
25567 |
52162 |
9599 |
19659 |
92140801 |
188708762 |
386484559 |
| 2005 |
26187 |
64693 |
10219 |
32190 |
104427961 |
328951761 |
1036209654 |
| 2006 |
28704 |
73742 |
12736 |
41239 |
162205696 |
525222585 |
1700672485 |
| 2007 |
30398 |
80007 |
14430 |
47504 |
208224900 |
685485758 |
2256650018 |
| Итого |
606784 |
1235106 |
0 |
0 |
2239108404 |
4856807884 |
12464089192 |
|