Задача №1
Зависимости координат от времени при движении материальной точки в плоскости 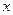 и и 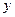 имеют вид: имеют вид:
 
Определить модуль скорость (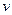 ) и ускорение ( ) и ускорение (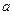 ) этой точки в момент времени ) этой точки в момент времени  . .
Решение
А. Модуль скорости материальной точки от времени выражается по формуле:
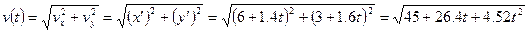
Следовательно, 
Б. . Модуль ускорения материальной точки от времени выражается по формуле:

Данные уравнения описывают движение материальной точки с постоянным ускорением  . .
Задача №2
Спутник вращается вокруг земли по круговой орбите на высоте 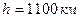 . Определите линейную и угловую скорости спутника. Ускорение свободного падения у поверхности Земли . Определите линейную и угловую скорости спутника. Ускорение свободного падения у поверхности Земли 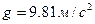 . Радиус Земли . Радиус Земли 
Решение
На спутник, движущийся по круговой орбите, действует сила тяжести  , которая во много раз превосходит силы тяготения, действующие на него со стороны других небесных тел, поэтому по второму закону Ньютона , которая во много раз превосходит силы тяготения, действующие на него со стороны других небесных тел, поэтому по второму закону Ньютона 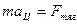 . Здесь . Здесь  — масса спутника, — масса спутника,  его центростремительное ускорение. По закону всемирного тяготения его центростремительное ускорение. По закону всемирного тяготения  . Здесь . Здесь  — гравитационная постоянная, — гравитационная постоянная, 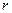 — расстояние от спутника до центра Земли, т.е. радиус круговой орбиты спутника ( — расстояние от спутника до центра Земли, т.е. радиус круговой орбиты спутника ( ), ),  — масса Земли. Центростремительное ускорение спутника — масса Земли. Центростремительное ускорение спутника  связано с линейной скоростью спутника связано с линейной скоростью спутника 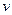 соотношением соотношением 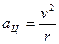 или или  . Следовательно, получаем уравнение движения спутника на высоте . Следовательно, получаем уравнение движения спутника на высоте 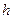 : :  или или 
Эту формулу можно упростить следующим образом. На тело массой  , находящееся на Земле, действует сила тяжести , находящееся на Земле, действует сила тяжести 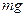 , равная по закону всемирного тяготения силе тяготения этого тела к Земле, поэтому , равная по закону всемирного тяготения силе тяготения этого тела к Земле, поэтому  или или  , откуда , откуда  . .
Таким образом, линейная скорость спутника равна 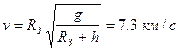 , ,
а угловая скорость 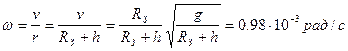
Задача №3
Шар массой 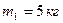 движется со скоростью движется со скоростью  и сталкивается с покоящимся шаром массой и сталкивается с покоящимся шаром массой  и скоростью и скоростью 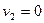 . Определить скорости шаров . Определить скорости шаров  и и 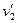 после удара, если он абсолютно упругий, прямой, центральный. после удара, если он абсолютно упругий, прямой, центральный.
Решение
Рассматриваемые в задаче оба шара образуют замкнутую систему и в случае упругого удара и импульс системы, и механическая (кинетическая) энергия сохраняется. Запишем оба закона сохранения (с учётом неподвижности второго шара до удара):
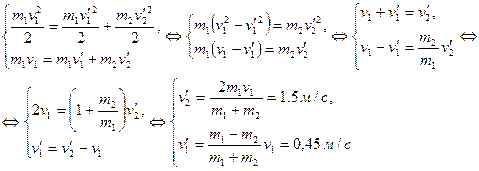
Таким образом, налетающий (первый) шар в результате удара уменьшил свою скорость с 1,05 м/с до 0,45 м/с, хотя и продолжил движение в прежнем направлении, а ранее неподвижный (второй) шар приобрёл скорость, равную 1,5 м/с и теперь оба шара движутся по одной прямой, и в одном направлении.
Задача №4
Баллон вместимостью 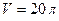 наполнен азотом при температуре наполнен азотом при температуре  . Когда часть газа израсходовалась давление понизилось на . Когда часть газа израсходовалась давление понизилось на  . Определить массу . Определить массу 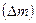 израсходованного газа. Процесс считать изотермическим (при постоянной температуре). израсходованного газа. Процесс считать изотермическим (при постоянной температуре).
Решение
Пусть  — молярная масса азота; — молярная масса азота;
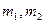 — начальная и конечная масса газа; — начальная и конечная масса газа; 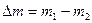 — расход газа. — расход газа.
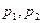 — начальное и конечное давление газа в баллоне; — начальное и конечное давление газа в баллоне; 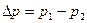 — снижение давления газа; — снижение давления газа;
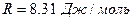 — универсальная газовая постоянная. — универсальная газовая постоянная.
Так как масса газа в баллоне меняется, то начальное и конечное состояния газа в баллоне нельзя связывать ни законом Бойля-Мариотта, ни законом Шарля.равнением газа в баллоне меняется, то начальное и конечное состояния газа в баллоне нельзя связывать законом Бойля-Мариотт Нужно для каждого состояния записать уравнение Менделеева-Клапейрона
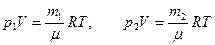 , тогда , тогда 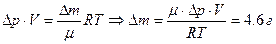
Задача №5
Вычислить плотность азота 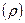 , находящегося в баллоне под давлением , находящегося в баллоне под давлением 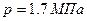 и имеющего температуру и имеющего температуру 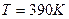 . .
Решение
Пусть  — молярная масса азота; — молярная масса азота;
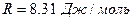 — универсальная газовая постоянная; — универсальная газовая постоянная;
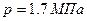 — давление газа в баллоне; — давление газа в баллоне;
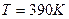 — температура газа в баллоне. — температура газа в баллоне.
Запишем уравнение Менделеева-Клапейрона для текущего состояния газа (с учётом, что 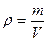 ): ):
 . .
|