Министерство образования и науки Российской Федерации
Курсовая работа
По дисциплине: Высшая математика
(Основы линейного программирования)
На тему: КРАТНЫЕ ИНТЕГРАЛЫ
Выполнил: ______________
Преподаватель:___________
Дата ___________________
Оценка _________________
Подпись ________________
ВОРОНЕЖ 2008
Содержание
1 Кратные интегралы
1.1 Двойной интеграл
1.2 Тройной интеграл
1.3 Кратные интегралы в криволинейных координатах
1.4 Геометрические и физические приложения кратных интегралов
2 Криволинейные и поверхностные интегралы
2.1 Криволинейные интегралы
2.2 Поверхностные интегралы
2.3 Геометрические и физические приложения
Список используемой литературы
1 Кратные интегралы
1.1
Двойной интеграл
Рассмотрим в плоскости Оху замкнутую область D, ограниченную линией L. Разобьем эту область какими-нибудь линиями на п частей  , а соответствующие наибольшие расстояния между точками в каждой из этих частей обозначим d1
, d2
, ..., dn
. Выберем в каждой части , а соответствующие наибольшие расстояния между точками в каждой из этих частей обозначим d1
, d2
, ..., dn
. Выберем в каждой части  точку Рi
. точку Рi
.
Пусть в области в задана функция z = f(x, y). Обозначим через f(P1
), f(P2
),…, f(Pn
) значения этой функции в выбранных точках и составим сумму произведений вида f(Pi
)ΔSi
:
 , (1) , (1)
называемую интегральной суммой для функции f(x, y) в области D.
Если существует один и тот же предел интегральных сумм (1) при  и и  , не зависящий ни от способа разбиения области в на части, ни от выбора точек Pi
в них, то он называется двойным интегралом от функции f(x, y) по области в и обозначается , не зависящий ни от способа разбиения области в на части, ни от выбора точек Pi
в них, то он называется двойным интегралом от функции f(x, y) по области в и обозначается
 . (2) . (2)
Вычисление двойного интеграла по области D, ограниченной линиями  x = a, x = b( a < b ), где φ1
(х) и φ2
(х) непрерывны на [a, b] (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла: x = a, x = b( a < b ), где φ1
(х) и φ2
(х) непрерывны на [a, b] (рис. 1) сводится к последовательному вычислению двух определенных интегралов, или так называемого двукратного интеграла:

Рис. 1
 = =  (3) (3)
1.2
Тройной интеграл
Понятие тройного интеграла вводится по аналогии с двойным интегралом.
Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Зададим в этой замкнутой области непрерывную функцию f(x, y, z). Затем разобьем область V на произвольные части Δvi
, считая объем каждой части равным Δvi
, и составим интегральную сумму вида
 , (4) , (4)
Предел при  интегральных сумм (11), не зависящий от способа разбиения области V и выбора точек Pi
в каждой подобласти этой области, называется тройным интегралом от функции f(x, y, z) по области V: интегральных сумм (11), не зависящий от способа разбиения области V и выбора точек Pi
в каждой подобласти этой области, называется тройным интегралом от функции f(x, y, z) по области V:
  . (5) . (5)
Тройной интеграл от функции f(x,y,z) по области V равен трехкратному интегралу по той же области:
  . (6) . (6)
1.3 Кратные интегралы в криволинейных координатах
Введем на плоскости криволинейные координаты, называемые полярными. Выберем точку О (полюс) и выходящий из нее луч (полярную ось).
 
Рис. 2 Рис. 3
Координатами точки М (рис. 2) будут длина отрезка МО – полярный радиус ρ и угол φ между МО и полярной осью: М(ρ,φ). Отметим, что для всех точек плоскости, кроме полюса, ρ > 0, а полярный угол φ будем считать положительным при измерении его в направлении против часовой стрелки и отрицательным – при измерении в противоположном направлении.
Связь между полярными и декартовыми координатами точки М можно задать, если совместить начало декартовой системы координат с полюсом, а положительную полуось Ох – с полярной осью (рис. 3). Тогда x=ρcosφ, у=ρsinφ . Отсюда  , tg , tg . .
Зададим в области D, ограниченной кривыми ρ=Φ1
(φ) и ρ=Φ2
(φ), где φ1 <
φ < φ2
, непрерывную функцию z = f(φ, ρ) (рис. 4).

Рис. 4
Тогда
 (7) (7)
В трехмерном пространстве вводятся цилиндрические и сферические координаты.
Цилиндрические координаты точки Р(ρ,φ,z) – это полярные координаты ρ, φ проекции этой точки на плоскость Оху и аппликата данной точки z (рис.5).
 
Рис.5 Рис.6
Формулы перехода от цилиндрических координат к декартовым можно задать следующим образом:
x = ρcosφ, y = ρsinφ, z = z. (8)
В сферических координатах положение точки в пространстве определяется линейной координатой r – расстоянием от точки до начала декартовой системы координат (или полюса сферической системы), φ – полярным углом между положительной полуосью Ох и проекцией точки на плоскость Оху, и θ – углом между положительной полуосью оси Оz и отрезком OP (рис.6). При этом

Зададим формулы перехода от сферических координат к декартовым:
x = rsinθcosφ, y = rsinθsinφ, z = rcosθ. (9)
Тогда формулы перехода к цилиндрическим или сферическим координатам в тройном интеграле будут выглядеть так:
 , (10) , (10)
где F1
и F2
– функции, полученные при подстановке в функцию fвместо x, y, z их выражений через цилиндрические (8) или сферические (9) координаты.
1.4 Геометрические и физические приложения кратных интегралов
1) Площадь плоской области S: (11) (11)
Пример 1.
Найти площадь фигуры D, ограниченной линиями 
у = 2, у = 5.
Решение.

Эту площадь удобно вычислять, считая у внешней переменной. Тогда границы области задаются уравнениями  и и

где  вычисляется с помощью интегрирования по частям: вычисляется с помощью интегрирования по частям:

Следовательно,

2) Объем цилиндроида, то есть тела, ограниченного частью поверхности S:z = f(x,y) , ограниченной контуром L, проекцией в этой поверхности на плоскость Оху и отрезками, параллельными оси Оz и соединяющими каждую точку контура L с соответствующей точкой плоскости Оху:
 (12) (12)
3) Площадь части криволинейной поверхности S, заданной уравнением z = f(x,y), ограниченной контуром L:
 (13) (13)
где в – проекция S на плоскость Оху.
4) Момент инерции относительно начала координат О материальной плоской фигуры D:
 (14) (14)
Пример 2.
Найти момент инерции однородной круглой пластинки
(x – a)2
+ (y – b)2
< 4b2
относительно начала координат.
Решение.
В силу однородности пластинки положим ее плотность γ(х,у) = 1.

Центр круга расположен в точке C(a, b), а его радиус равен 2b.
Уравнения границ пластинки имеют вид


Вычислим каждый из полученных интегралов отдельно.
Для вычисления интеграла I1
сделаем замену: 
 при x = a – 2b при x = a – 2b  при x = a + 2b при x = a + 2b 

Для вычисления интеграла I2
преобразуем подынтегральную функцию по формуле разности кубов:

Тогда

Следовательно, 
Моменты инерции фигуры в относительно осей Ох и Оу:
 (15) (15)
5) Масса плоской фигуры в переменной поверхностной плотности γ = γ (х, у):
 (16) (16)
Пример 3.
Найти массу пластинки в плотности γ = ух3
, если 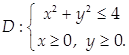
Решение.


Координаты центра масс плоской фигуры переменной поверхностной плотности γ = γ (х, у):
 (17) (17)
Пример 4.
Найти центр тяжести однородной пластины D, ограниченной кривыми у2
= ах и 
Решение.
Так как пластина однородна, т.е. ее плотность постоянна, то можно принять ее за единицу.

Тогда 
Найдем массу пластины, а для этого определим абсциссу точки пересечения ограничивающих ее линий:

Соответственно
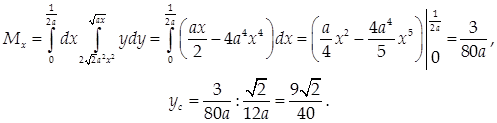
6) Объем тела V:
 (18) (18)
Пример 5.
Найти объем тела V, ограниченного поверхностями 

Решение.
Найдем проекцию тела на плоскость Оху (при этом заметим, что плоскость  проектируется на эту плоскость в виде прямой х = 0): проектируется на эту плоскость в виде прямой х = 0):

Определим абсциссу точки пересечения кривых у = х2
и х + у = 2:
 посторонний корень. Тогда, используя формулу (18), получаем: посторонний корень. Тогда, используя формулу (18), получаем:

7) Масса тела V плотности γ = γ (x, y, z):
 (19) (19)
8) Моменты инерции тела V относительно координатных осей и начала координат:

 (20) (20)

 (21) (21)
где γ (х, y, z) – плотность вещества.
Статические моменты тела относительно координатных плоскостей Oyz, Oxz, Oxy:
 (22) (22)
9) Координаты центра масс тела:

 
II
. Криволинейные и поверхностные интегралы
2.1
Криволинейные интегралы
Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части Δsi
длиной Δsi
и выберем на каждой из частей точку Mi
. Назовем в длину наибольшего отрезка кривой:  . .
Криволинейным интегралом первого рода от функции f по кривой L называется предел интегральной суммы  , не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi
: , не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi
:
 (24) (24)
Если кривую L можно задать параметрически:
x = φ(t), y = ψ(t), z = χ(t), t0
≤ t ≤ T,
то способ вычисления криволинейного интеграла первого рода задается формулой
 (25) (25)
В частности, если кривая L задана на плоскости явным образом:
у=φ(х), где х1
≤ х ≤ х2
, формула (40) преобразуется к виду:
 . (26) . (26)
Теперь умножим значение функции в точке Mi
не на длину i-го отрезка, а на проекцию этого отрезка, скажем, на ось Ох, то есть на разность xi
– xi
-
1
= Δxi
.
Если существует конечный предел при  интегральной суммы интегральной суммы  , не зависящий от способа разбиения кривой на отрезки и выбора точек Mi
, то он называется криволинейным интегралом второго рода от функции f(M) по кривой L и обозначается , не зависящий от способа разбиения кривой на отрезки и выбора точек Mi
, то он называется криволинейным интегралом второго рода от функции f(M) по кривой L и обозначается
  . (27) . (27)
Подобным образом можно определить и криволинейные интегралы 2-го рода вида

Если вдоль кривой L определены функции P(M)=P(x, y, z), Q(M) = Q(x, y, z), R(M) = R(x, y, z), которые можно считать компонентами некоторого вектора  , и существуют интегралы , и существуют интегралы
 , ,
тогда их сумму называют криволинейным интегралом второго рода (общего вида) и полагают
 . .
Если кривая L задана параметрическими уравнениями
x = φ(t), y = ψ(t), z = χ(t), α ≤ t ≤ β ,
где φ, ψ, χ – непрерывно дифференцируемые функции, то
 . (28) . (28)
Связь между двойным интегралом и криволинейным интегралом 2-го рода задается формулой Грина:
 (29) (29)
где L – замкнутый контур, а в – область, ограниченная этим контуром.
Необходимыми и достаточными условиями независимости криволинейного интеграла

от пути интегрирования являются:
 . (30) . (30)
При выполнении условий (30) выражение Pdx + Qdy +Rdzявляется полным дифференциалом некоторой функции и. Это позволяет свести вычисление криволинейного интеграла к определению разности значений и в конечной и начальной точках контура интегрирования, так как
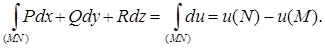
При этом функцию и можно найти по формуле
 (31) (31)
где (x0
, y0
, z0
) – точка из области D, aC – произвольная постоянная.
2.2
Поверхностные интегралы
Рассмотрим некоторую поверхность S, ограниченную контуром L, и разобьем ее на части S1
, S2
,…, Sп
(при этом площадь каждой части тоже обозначим Sп
). Пусть в каждой точке этой поверхности задано значение функции f(x, y, z). Выберем в каждой части Si
точку
Mi
(xi
, yi
, zi
) и составим интегральную сумму
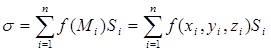
Если существует конечный предел при  этой интегральной суммы, не зависящий от способа разбиения поверхности на части и выбора точек Mi
, то он называется поверхностным интегралом первого рода от функции f(M) = f(x, y, z) по поверхности S и обозначается этой интегральной суммы, не зависящий от способа разбиения поверхности на части и выбора точек Mi
, то он называется поверхностным интегралом первого рода от функции f(M) = f(x, y, z) по поверхности S и обозначается
 . (32) . (32)
Если поверхность S задается явным образом, то есть уравнением вида z = φ(x, y), вычисление поверхностного интеграла 1-го рода сводится к вычислению двойного интеграла:
 (33) (33)
где Ω – проекция поверхности S на плоскость Оху.
Разобьем поверхность Sна части S1
, S2
,…, Sп
, выберем в каждой части Si
точку Mi
(xi
, yi
, zi
), и умножим f(Mi
) на площадь Di
проекции части Si
на плоскость Оху. Если существует конечный предел суммы
 , ,
не зависящий от способа разбиения поверхности и выбора точек на ней, то он называется поверхностным интегралом второго рода от функции f(M) по выбранной стороне поверхности S и обозначается
 (34) (34)
Подобным образом можно проектировать части поверхности на координатные плоскости Оxzи Оyz. Получим два других поверхностных интеграла 2-го рода:
 и и 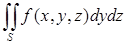 . .
Рассмотрев сумму таких интегралов по одной и той же поверхности соответственно от функций P(x, y, z), Q(x, y, z), R(x, y, z), получим поверхностный интеграл второго рода общего вида:
 (35) (35)
Если D, D΄ и D΄΄ - проекции поверхности S на координатные плоскости Оху, Oxz и Oyz, то
 (36) (36)
Связь между тройным интегралом по трехмерной области V и поверхностным интегралом 2-го рода по замкнутой поверхности S, ограничивающей тело V, задается формулой Гаусса-Остроградского:
  (37) (37)
где запись «S+
» означает, что интеграл, стоящий справа, вычисляется по внешней стороне поверхности S.
Формула Стокса устанавливает связь между поверхностным интегралом 1-го рода по поверхности σ и криволинейным интегралом 2-го рода по ограничивающему ее контуру λ с учетом ориентации поверхности:
 (38) (38)
2.3 Геометрические и физические приложения
1) Длина кривой.
Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:
 (39) (39)
2) Масса кривой.
Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле
 (40) (40)
Пример 6.
Найти массу кривой с линейной плотностью  заданной в полярных координатах уравнением ρ = 4φ, где заданной в полярных координатах уравнением ρ = 4φ, где 
Решение.
Используем формулу (40) с учетом того, что кривая задана в полярных координатах:

3) Моменты кривой l:
 - (41) - (41)
- статические моменты плоской кривой l относительно осей Ох и Оу;
 - (42) - (42)
- момент инерции пространственной кривой относительно начала координат;
 - (43) - (43)
- моменты инерции кривой относительно координатных осей.
4) Координаты центра масс кривой вычисляются по формулам
 . (44) . (44)
5) Работа силы  , действующей на точку, движущуюся по кривой (АВ): , действующей на точку, движущуюся по кривой (АВ):
 , (45) , (45)
Пример 7.
Вычислить работу векторного поля  вдоль отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2). вдоль отрезка прямой от точки А(-2;-3;1) до точки В(1;4;2).
Решение.
Найдем канонические и параметрические уравнения прямой АВ:

6) Площадь криволинейной поверхности, уравнение которой
z = f(x, y), можно найти в виде:
 (46) (46)
(Ω – проекция S на плоскость Оху).
7) Масса поверхности
 (47) (47)
Пример 8.
Найти массу поверхности 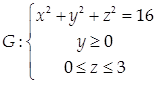 с поверхностной плотностью γ = 2z2
+ 3. с поверхностной плотностью γ = 2z2
+ 3.
Решение.

На рассматриваемой поверхности 
 Тогда Тогда

Проекцией в этой поверхности на координатную плоскость Оху является полукольцо с границами в виде дуг концентрических окружностей радиусов 3 и 4.

Применяя формулу (47) и переходя к полярным координатам, получим:

8) Моменты поверхности:
 (48) статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz; (48) статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;
 (49) (49)
- моменты инерции поверхности относительно координатных осей;
 - (50) - (50)
- моменты инерции поверхности относительно координатных плоскостей;
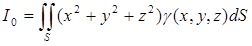 - (51) - (51)
- момент инерции поверхности относительно начала координат
9) Координаты центра масс поверхности:
 . (52) . (52)
Список используемой литературы
1. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. М.: Наука, 1999.
2. Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука, 2000.
3. Ильин В.А., Позняк Э.Г. Математический анализ. М.: Наука, 1999.
4. Смирнов В.И. Курс высшей математики.- Т.2. М.: Наука, 2005.
5. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М.: Наука, 2001.
6. Пискунов Н.С. Дифференциальное и интегральное исчисление. – Т.2. М.: Наука, 2001.
7. Сборник задач по математике для втузов. Специальные разделы математического анализа (под редекцией А.В.Ефимова и Б.П.Демидовича). – Т.2. М.: Наука, 2004.
8. Мышкис А.Д. Лекции по высшей математике. М.: Наука, 2003.
9. Титаренко В.И., Выск Н.Д. Кратные, криволинейные и поверхностные интегралы. Теория поля. М.: МАТИ, 2006.
|