МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ ТАТАРСТАН
АЛЬМЕТЬЕВСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ИНСТИТУТ
Кафедра физики
Реферат
на тему:«Закон кубов Дебая»
Выполнил студентгруппы 18-13В Гонтарь И. В. Преподаватель: Мухетдинова З. З.
Альметьевск 2010
Содержание:
1. Энергия кристаллической решетки …………………………… 3
2. Модель Эйнштейна …………………………………………….. 6
3. Модель Дебая ………………………………………………….. 7
4. Закон кубов Дебая ……………………………………………… 8
5. Достижения Дебая ……………………………………………… 9
6. Список литературы …………………………………………….. 12
Энергия кристаллической решетки
Особенность твердого тела - наличие дальнего и ближнего порядков. В идеальном кристалле частицы занимают определенные положения и не надо учитывать N! при статистических расчетах.
Энергия кристаллической решетки одноатомного кристалла состоит из двух основных вкладов: E = Uo
+ Eкол
. Колеблются атомы в решетке. У многоатомных частиц, образующих кристалл, надо учитывать и внутренние степени свободы: колебания и вращения. Если не учитывать ангармоничность колебаний атомов, дающую зависимость Uo
от температуры (изменение равновесных положений атомов), Uo
можно приравнять потенциальной энергии кристалла и не зависящей от Т. При Т = 0 энергия кристаллической решетки, т.е. энергия для удаления частиц кристалла на бесконечное расстояние будет равна Екр
= - Eо
= - ( Uo
+ Eо,кол
).
Здесь Eо,кол
- энергия нулевых колебаний. Обычно эта величина имеет порядок 10 кДж/ моль и много меньше Uo.
Считают Екр = - Uo. (Метод наибольшего слагаемого). Екр в ионных и молекулярных кристаллах до 1000 кДж/моль, в молекулярных и в кристаллах с водородными связями: до 20 кДж/моль (СР4
- 10, Н2
О - 50). Величины определяют из опыта или считают на основе какой-либо модели: ионное взаимодействие по кулону, ван-дер-ваальсовы силы по потенциалу Сазерленда.
Рассмотрим ионный кристалл NaCl, имеющий гранецентрированную кубическую решетку: в решетке у каждого иона 6 соседей противоположного знака на расстоянии R, в следующем втором слое 12 соседей того же знака на расстоянии 21/2
R, 3-ий слой: 8 ионов на расстоянии 31/2
R, 4-ый слой: 6 ионов на расстоянии 2R и т.д.
Потенциальная энергия кристалла из 2N ионов будет U = Nu, где u - энергия энергия взаимодействия иона с соседями. Энергия взаимодействия ионов состоит из двух членов: короткодействующего отталкивания за счет валентных сил (1-й член) и притяжения или отталкивания зарядов: 
знак + для отталкивание одинаковых, - притяжения разных ионов. e -заряд. Введем величину приведенного расстояния рij
= rij
/ R, где rij
- расстояние между ионами, R - параметр решетки.
Энергия взаимодействия иона со всеми соседями 
где
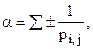постоянная Маделунга = 6/1 - 12/21/2
+ 8/31/2 -
6/2 + .... Здесь - для одинаковых по знаку заряда ионов, + для разных. Для NaCl a = 1,747558... An
= S 1/ pij
n
в первом члене. Расстояние Ro
(половина ребра куба в данном случае) отвечает минимуму потенциальной энергии при Т = 0 и его можно определить из данных кристаллографии и зная потенциал отталкивания. Очевидно, что 
и тогда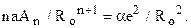 
Отсюда находим An
и энергия 
или 
.
n - параметр потенциала отталкивания и обычно ³ 10, т.е. основной вклад вносит кулоновское взаимодействие (считаем при этом, что R заметно не зависит от Т), а отталкивание дает менее 10%.
Для NaCl кулоновское взаимодействие 862, отталкивание 96 кДж/моль (n = 9). Для молекулярных кристаллов можно считать по потенциалу 6-12 и энергия будет равна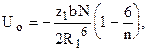 
z1
- число атомов в 1-ой координационной сфере, R1
- радиус первой координационной сферы, b - параметр потенциала.
Для неионных кристаллов надо учитывать колебательную составляющую энергии. Поступательные и вращательные движения при абсолютном нуле отсутствуют. Остается колебательная составляющая энергии. Колебаний 3N - 6, но поступательные и вращательные относятся к кристаллу в целом. Грубо можно считать 3N, т.к. N (велико, число частиц в кристалле). Тогда все 3N степеней свободы кристалла из N частиц колебательные. В принципе легко посчитать сумму по состояниям и термодинамические функции. Но надо знать спектр частот колебаний кристалла. Дело в том, что смещение частицы вызывает смещение других и осцилляторы связаны. Полная сумма по состояниям колебательного движения будет определена:
.
Т.к. это кристалл, то на N ! делить не надо. Средняя энергия равна производной lnZ по Т при постоянном V, умноженной на kT2
. Отсюда энергия решетки равна сумме вкладов потенциальной и колебательной энергии, 
а энтропия S = E/ T + k ln(Z).
Для расчета используют две основные модели.
Модель Эйнштейна
Все частоты считаются одинаковыми: совокупность одномерных гармонических осциллятров. Сумма по состояниям трехмерного осциллятора состоит из 3 одинаковых членов q = [ 2sh(hn/ 2kT)]-3
. Для N частиц будет 3N сомножителей. Т.е. энергия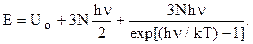 
При высоких Т, разлагая экспоненту в ряд, предел sh(hn/ 2kT) = hn/ 2kT и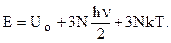 
Энтропия колебательного движения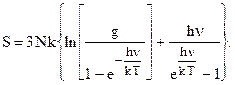 
Теплоемкость кристаллов: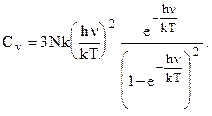 
У ОП ошибка. Отсюда при больших Т >> qЭ
= hn/ k предел Cv
® 3Nk: Закон Дюлонга-Птидля одноатомных кристаллов. И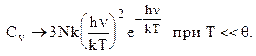
(Экспонента быстро стремится к 0).
В классическом приближении Екол
без нулевых колебаний равна 3NkT и вклад колебаний в теплоемкость 3Nk = 3R. Расчет по Эйнштейну: нижняя кривая, более заметно отклоняющаяся от опытных данных.
Модель Эйнштейна дает уравнение состояния твердого тела: (по Мелвин-Хьюзу)
uo
= - q возгонки, m, n - опытные параметры, так для ксенона m = 6, n = 11, ao
- межатомное расстояние при Т = 0. Т.е. pV/ RT = f(n, ao
, n, m).
Но вблизи Т = 0 предположения Эйнштейна об одинаковых частотах не работает. Осцилляторы могут различаться силой взаимодействия и частотой. Опыт при низких температурах показывает кубическую зависимость от температуры.
Модель Дебая
Дебай предложил модель существования непрерывного спектра частот (строго для низких частот, для тепловых колебаний - фононов) вплоть до некой максимальной. Функция распределения по частотам гармонических осцилляторов имеет вид
, где cl
, ct
- скорости распространения продольных и поперечных волн колебаний. При частотах выше максимальной g = 0.
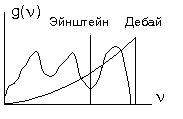
Площади под двумя кривыми должны быть одинаковыми. Реально существует некоторый спектр частот, кристалл неизотропен (обычно этим пренебрегают и полагают скорости распространения волн по направлениям одинаковыми). Может быть, что максимальная частота Дебая выше реально существующих, что следует из условия равенства площадей. Значение максимальной частоты определяется по условию, что полное число колебаний равно 3N (при этом пренебрегаем дискретностью энергии) 
и 
, с - скорость движения волны. Полагаем, что скорости cl
и ct
равны. Характеристическая температура Дебая QD
= hnм
/ k.
Введем х = hn/ kT. Средняя энергия колебаний тогда при максимальном
хм
= Q D
/ T
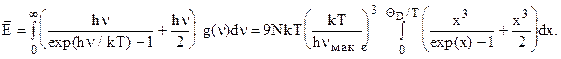
Второй член под интегралом даст Е нулевых колебаний Ео
= (9/8)NkQD
и тогда колебательная энергия кристалла:
Так как Uo
и Еo
не зависят от Т, то вклад в теплоемкость даст 2-й член в выражении для энергии.
Введем функцию Дебая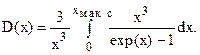 
При высоких Т получим очевидное D(x) ® 1. Дифференцируя по х, получим 
.
При высоких Т предел CV
= 3Nk, а при низких: 
.
При малых Т верхний предел интегрирования стремится к бесконечности, E - Eo
= 3Rp4
T4
/5QD
3
и получим формулу для определения Cv
при Т® 0: где
 
Получили Закон кубов Дебая
.
Закон кубов Дебая.
Характеристическая температура Дебая зависит от плотности кристалла и скорости распространения колебаний (звука) в кристалле. Строго интеграл по Дебаю надо решать на ЭВМ.
Характеристическая температура Дебая (Физ. энциклопедия)
Na 150 Cu 315 Zn 234 Al 394 Ni 375 Ge 360 Si 625
A.У 157 342 316 423 427 378 647
Li 400 K 100 Be 1000 Mg 318 Ca 230 B 1250 Ga 240
As 285 Bi 120 Ar 85 In 129 Tl 96
W 310 Fe 420
Ag 215 Au 170 Cd 120 Hg 100 Gd 152 Pr 74 Pt 230
La 132 Cr 460 Mo 380 Sn(белое) 170, (серое) 260 C(алмаз) 1860
Для оценки характеристической температуры Дебая можно пользоваться эмпирической формулой Линдеманна: QD
=134,5[Тпл/ (АV2/3
)]1/2
, здесь А - атомная масса металла. Для температуры Эйнштейна аналогично, но 1-ый множитель берут 100.
Достижения Дебая
Дебай – автор фундаментальных трудов по квантовой теории твердого тела. В 1912 он ввел представление о кристаллической решетке как об изотропной упругой среде, способной совершать колебания в конечном диапазоне частот (модель твердого тела Дебая). Исходя из спектра этих колебаний показал, что при низких температурах теплоемкость решетки пропорциональна кубу абсолютной температуры (закон теплоемкости Дебая). В рамках своей модели твердого тела ввел понятие характеристической температуры, при которой для каждого вещества становятся существенными квантовые эффекты (температура Дебая). В 1913 вышла одна из самых известных работ Дебая, посвященная теории диэлектрических потерь в полярных жидкостях. Примерно в это же время были опубликованы его работы по теории дифракции рентгеновских лучей. С изучением дифракции связано начало экспериментальной деятельности Дебая. Вместе со своим ассистентом П.Шеррером он получил рентгенограмму тонко измельченного порошка LiF. На фотографии были отчетливо видны кольца, получающиеся при пересечении рентгеновских лучей, дифрагировавших от случайно ориентированных кристалликов вдоль образующих конусов, с фотопленкой. Метод Дебая – Шеррера, или метод порошков, долгое время применялся в качестве основного при рентгеноструктурном анализе. В 1916 Дебай совместно с А.Зоммерфельдом применил условия квантования для объяснения эффекта Зеемана, ввел магнитное квантовое число. В 1923 объяснил эффект Комптона. В 1923 Дебай в соавторстве со своим ассистентом Э.Хюккелем опубликовал две большие статьи по теории растворов электролитов. Изложенные в них представления послужили основой теории сильных электролитов, получившей название теории Дебая – Хюккеля. С 1927 интересы Дебая сосредоточились на вопросах химической физики, в частности на изучении молекулярных аспектов диэлектрического поведения газов и жидкостей. Он занимался также исследованием дифракции рентгеновских лучей на изолированных молекулах, что позволило определить структуру многих из них.
Основным объектом научных интересов Дебая во время его работы в Корнеллском университете стала физика полимеров. Он разработал метод определения молекулярного веса полимеров и их формы в растворе, основанный на измерении рассеяния света. Одна из последних его крупных работ (1959) была посвящена вопросу, чрезвычайно актуальному и сегодня, – изучению критических явлений. Среди наград Дебая – медали Х.Лоренца, М.Фарадея, Б.Румфорда, Б.Франклина, Дж.Гиббса (1949), М.Планка (1950) и др. Умер Дебай в Итаке (США) 2 ноября 1966.
Дебай — выдающийся, представитель голландской науки — получил Нобелевскую премию по химии в 1936 г. Обладая исключительной разносторонностью, он внес большой вклад в развитие не только химии, но и физики. Эти заслуги принесли Дебаю большую известность; ему присвоили почетные звания Доктора наук более 20 университетов мира (Брюссельский, Оксфордский, Бруклинский, Бостонский и другие). Он был награжден многими медалями и премиями, в том числе Фарадея, Лоренца. Планка. С 1924 г. Дебай — чл.-корр. АН СССР.
Список литературы
1. Бушманов Б.Н., Хромов Ю.А. Физики твёрдого тела. - М.,1971г.
2. Детлаф А.А.Курс физики. - М.,1973г.
3. Даниленко В.М. Что такое твёрдое тело? - Киев,1983г.
4. Китайгородский А.И. и Федин Э.И. Атомное строение и свойства твёрдых тел. - М.,1963г.
|