Учебное пособие: Исследование функций и построение их графиков
|
Название: Исследование функций и построение их графиков Раздел: Рефераты по математике Тип: учебное пособие | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тема 1. Предел функции Число А называется пределом функции Для предела функции вводится обозначение Пределы функций обладают следующими основными свойствами: Функция не может иметь более одного предела. Если Если существует
Если существуют
Операция предельного перехода перестановочна с операцией вычисления непрерывной функции, т. е. справедлива формула Если функция Функция Пример 1. Пример 2. В рассмотренных примерах предел находился сразу: в виде числа или символа Для раскрытия неопределенностей используются специальные приемы и два следующих предела, которые играют особую роль в математике и поэтому называются замечательными: - первый замечательный предел -второй замечательный предел Пример 3. Решение. Непосредственной подстановкой убеждаемся, что имеем дело с неопределенностью вида
Для раскрытия неопределенности разложим числитель и знаменатель на множители. Найдем корни многочлена, стоящего в числителе. Для этого составим уравнение второй степени
Тогда для квадратного трехчлена справедливо разложение на множители
Аналогичные действия выполним для многочлена, стоящего в знаменателе. Уравнение
и знаменатель представляется в виде: Сократим дробь на множитель
Пример 4. Решение. Непосредственной подстановкой убеждаемся, что возникает неопределенность вида
= Пример 5. Решение. Имеем неопределенность вида
Пример 6. Решение. При
Пользуясь свойствами пределов и первым замечательным пределом, далее имеем:
Пример 7. Решение. Имеем неопределенность вида [
Выделим у дроби целую часть
Введем новую переменную
Заметим, что при
= Неопределенности вида Пример 8. Первоначальный вклад в банк составил Решение. При
Если начислять проценты по вкладам не один раз в год, а
Тогда размер вклада за
Здесь при решении использовался второй замечательный предел. Подставляя исходные числовые данные задачи, получаем
Вопросы для самопроверки Дайте определение предела функции в точке. Назовите основные свойства пределов функций. Какие виды неопределенностей встречаются при нахождении пределов? Какие пределы называются замечательными? Какие функции называют бесконечно малыми? Задачи для самостоятельной работы Найти пределы следующих функций:
Таблица 1. Тема 2. Производная функции Приращением функции Производной функции
Нахождение производной функции называется дифференцированием этой функции. Если функция Важнейшими правилами дифференцирования являются следующие. Производная постоянной Постоянный множитель выносится за знак производной
Производная суммы (разности) функций равна сумме (разности) производных этих функций
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго
Производная частного двух дифференцируемых функций находится по формуле
Пусть переменная Если
Если функция, производную которой нужно найти, представляет из себя комбинацию элементарных функций, то для вычисления производной применяются правила дифференцирования и таблица производных элементарных функций, приводимая ниже. Таблица 2.
Пример 1. Найти производную функции
Решение. Представим ее как сложную функцию. Пусть
В свою очередь, промежуточный аргумент
= Отсюда производная искомой функции
Пример 2. Найти производную функции
Решение. Обозначим Производную
Второй сомножитель
Наконец, последняя производная
= В итоге получаем искомую производную
Пример 3. Наити производную
Решение. Производная суммы двух функций есть сумма их производных
Для нахождения производной первого слагаемого Тогда
= Производную второго слагаемого
Отсюда
Наконец, находим производную искомой функции
Пример 4. На основе опытных данных построена математическая модель спроса
Определить эластичность спроса при Решение. Эластичностью спроса
Если Найдем производную
Тогда
Определим эластичность спроса при Правило Лопиталя. При нахождении пределов функций (тема 1) неопределенности вида
Если
В общем случае правило Лопиталя можно применять неоднократно. Пример 5. Найти
Решение. Для раскрытия неопределенности применим правило Лопиталя.
Неопределенность вида
Вопросы для самопроверки Дайте определение производной функции в точке. Какая функция называется дифференцируемой в точке? Назовите важнейшие правила дифференцирования. Как находится производная сложной функции? Сформулируйте правило Лопиталя. Задачи для самостоятельной работы Найти производные следующих функций: Таблица 3.
Тема 3. Применение дифференциала функции в приближенных вычислениях Дифференциалом функции
Отсюда приращение функции
Приведенная формула используется в приближенных вычислениях. Пример. Вычислить приближенно Решение. Рассмотрим функцию
В качестве - значение - число В нашем случае этим требованиям удовлетворяет число Применяя формулу, находим искомое число:
Вопросы для самопроверки 1. Дайте определение дифференциала функции в точке. 2. Почему формула, используемая для вычислений, является приближенной? 3. Каким условиям должно удовлетворять число Задачи для самостоятельной работы Вычислить приближённое значение Таблица 4.
Тема 4. Исследование функций и построение их графиков Если функция одной переменной задана в виде формулы Пример 1. Значение функции Пример 2. Функция
не определена при таких значениях аргумента Пример 3. Функция Функция
и нечетной, если справедливо другое соотношение: Пример 4. Пусть
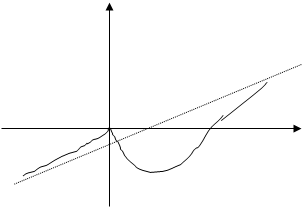
Таким образом, эта функция является четной. Для функции Их сумма Асимптотой графика функции
2
а)
в) Вертикальные асимптоты функции следует искать либо в точках разрыва второго рода (хотя бы один из односторонних пределов функции равен в точке бесконечности или не существует), либо на концах ее области определения (a,b), если a,b –конечные числа. Если функция Если существуют конечные пределы
то прямая Функция
Множество Справедливо следующее достаточное условие монотонности функции: если производная дифференцируемой функции внутри множества Пример 5. Дана функция Решение. Найдем ее производную Точка
Значение функции в точке Для того, чтобы функция Точки, в которых производная функции равна нулю, называются стационарными точками функции. В стационарной точке не обязательно должен быть экстремум функции. Для нахождения экстремумов требуется дополнительно исследовать стационарные точки функции, например, путем использования достаточных условий экстремума. Первое из них заключается в том, что если при переходе через стационарную точку Если же изменение знака производной при переходе через исследуемую точку не происходит, то в данной точке экстремума нет. Второе достаточное условие экстремума функции в стационарной точке использует вторую производную функции: если Функция
Если вторая производная дважды дифференцируемой функции Точкой перегиба графика непрерывной функции Вторая производная Если вторая производная при переходе через некоторую точку При исследовании функции и построении ее графика рекомендуется использовать следующую схему: Найти область определения функции. Исследовать функции на четность – нечетность (если функция четная или нечетная, то график достаточно исследовать только для положительных значений Найти вертикальные асимптоты. Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты. Найти интервалы возрастания и убывания функции и точки экстремума. Найти интервалы выпуклости и вогнутости функции и точки перегиба. Найти точки пересечения функции с осями координат. Пример 6. Исследовать функцию
и построить ее график. Решение. 1.Функция представляет многочлен 3-й степени, поэтому она определена и непрерывна для всех 2. Найдем значение функции при (-
а также Таким образом, исследуемая функция является функцией общего вида и ее требуется исследовать на всей числовой оси. Функция непрерывна на всей числовой оси, точек разрыва второго рода не имеет, следовательно, у нее вертикальные асимптоты отсутствуют. Рассмотрим поведение функции в бесконечности. Найдем пределы:
Так как пределы не являются конечными, то горизонтальных асимптот у функции нет. Далее проверим наличие у функции наклонных асимптот. Вычислим предел:
Поскольку предел не является конечными, то наклонные асимптоты также отсутствуют. Если бы предел являлся конечным и равнялся k, то требовалось найти другой предел
В случае когда он также конечен (равен числу b), устанавливается наличие наклонной асимптоты с уравнением Для определения интервалов монотонности функции найдем ее производную:
Производная также определена и непрерывна на всей числовой оси. Отсюда критическими точками могут быть только те, где производная равна нулю. Для нахождения стационарных точек функции приравниваем производную нулю:
и решаем квадратное уравнение:
Теперь можно записать:
В итоге функция имеет две стационарные точки Используя метод интервалов, найдем интервалы знакопостоянства производной функции.
1 _ 5/3 При При 1< Поскольку при В другой стационарной точке Для нахождения интервалов выпуклости вычислим вторую производную функции:
Вторая производная также определена на всей числовой оси и точки, где она не существует, отсутствуют. Приравнивая вторую производную к нулю:
находим точку Если В итоге, поскольку при переходе точки Определим точки пересечения функции с координатными осями. Полагая аргумент Записывая уравнение
найдем точки пересечения графика с осью абсцисс. Методом перебора из делителей свободного члена (равного 4) определяем, что
0 Отсюда уравнение можно записать в виде
Решением квадратного уравнения Для удобства построения графика полученные результаты запишем в следующую таблицу. Таблица 5.
График исследуемой функции Вопросы для самопроверки 1. Что называют асимптотой графика функции? 2. Что такое локальный экстремум функции? 3. Сформулируйте необходимое и достаточные условия локального экстремума. 4. Дайте определение выпуклой функции. 5. Какую точку графика называют точкой перегиба? Задачи для самостоятельной работы Исследовать и построить график функций: Таблица 6
Тема 5. Неопределенный интеграл Функция Отсюда следует, что если Совокупность всех первообразных функций для данной функции Если
где Операция нахождения неопределенного интеграла от некоторой функции называется интегрированием этой функции. Отметим основные свойства неопределенного интеграла. Производная от неопределенного интеграла равна подынтегральной функции, т.е.
Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
Постоянный множитель можно выносить за знак интеграла
Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций в отдельности
Основу вычислительного аппарата интегрального исчисления составляет таблица неопределенных интегралов от основных элементарных функций, приводимая ниже. Таблица 7.
Пример 1. Найти интеграл Решение. Воспользуемся табличным интегралом от степенной функции (п.3 в таб.7) для
Проверим правильность вычисления дифференцированием правой части
Получена подынтегральная функция, что говорит о правильном нахождении неопределенного интеграла. При вычислении неопределенных интегралов приведенную таблицу дополняют специальными приемами и методами интегрирования, два из которых рассмотрены ниже. Интегрирование заменой переменной (подстановкой) Замена переменной – один из самых эффективных приемов интегрирования, который основывается на следующем. Пусть требуется найти Тогда
Удачная замена переменной позволяет упростить исходный интеграл и в ряде случаев свести его к табличному. Пример 2. Найти Решение. Положим
Полученный интеграл относится к табличным и, следовательно,
Сделаем проверку дифференцированием:
Полученная производная совпадает с подынтегральной функцией исходного интеграла, что говорит о правильности вычислений. Пример 3. Вычислить Решение. Чтобы выявить замену, посредством которой может быть вычислен этот интеграл, преобразуем его к виду
Если положить
Интегрирование по частям Этот метод основывается на следующем утверждении. Пусть функции причем справедлива формула
называемая формулой интегрирования по частям. Пример 4. Найти Решение. Положим
Произвольную постоянную
Иногда формулу интегрирования по частям приходится применять неоднократно. Пример 5. Вычислить Решение. Полагая
Применяя формулу интегрирования по частям, получим
Степень переменной жим Отсюда Тогда
Вопросы для самоконтроля Дайте определение первообразной функции. Что называют неопределенным интегралом? Перечислите основные свойства неопределенного интеграла. В чем суть приема, называемого заменой переменной? На чем основан метод интегрирования по частям? Задачи для самостоятельной работы Найти неопределенные интегралы, результаты проверить дифференцированием:
Тема 6. Дифференциальные уравнения 1-го порядка Дифференциальным уравнением (ДУ) называют уравнение, связывающее искомую функцию одной или нескольких переменных, эти переменные и производные различных порядков данной функции. В случае, когда искомая функция зависит от одной переменной, дифференциальное уравнение называется обыкновенным. В общем виде оно записывается:
Порядок Решением уравнения называется такая функция Общим решением ДУ вида (1)
где Частным решением ДУ называется решение, получаемое из общего решения при конкретных числовых значениях постоянных Дифференциальное уравнение 1-го порядка, разрешенное относительно производной, записывается в общем виде
Его общим решением является функция одной произвольной постоянной
Для получения однозначного решения требуется задать начальное условие, которое геометрически представляет собой задание точки плоскости, через которую проходит данная интегральная кривая. Например, оно может быть записано в виде
С использованием данного условия общее решение (3) запишется
что позволяет определить из полученного соотношения конкретное значение постоянной ДУ 1-го порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде
Для нахождения общего решения такого уравнения его преобразовывают к виду, в котором дифференциал
Затем интегрируются обе части полученного равенства (с одной общей постоянной)
Пример 1. Найти общее решение следующего ДУ: Решение. Сначала преобразуем уравнение к виду (4)
а затем к виду (5):
Найдем интеграл от левой части. Для этого представим подынтегральную функцию в виде следующей суммы
Приравнивая числители, получаем
Найдем из последнего равенства При Отсюда
Интеграл от правой части Запишем произвольную постоянную в виде Тогда
Отсюда
Разрешая относительно
Дифференциальное уравнение 1-го порядка называется линейным, если оно имеет вид
Если Один из вариантов решения уравнения (6) сводится к представлению решения в виде произведения двух функций
одна из которых является произвольной, а другая определяется из уравнения (6). Так как
то подставляя (7) и (8) в уравнение (6), получим:
Полагая функцию
которое является уравнением с разделяющимся переменным. Тогда при определенной
которая также является дифференциальным уравнением с разделяющимися переменными. Найденные Пример 2.Найти общее и частное решение уравнения Решение. Разделим левую и правую часть на
Получили линейное неоднородное уравнение. Пусть
Потребуем:
Отсюда, разделяя переменные
и проинтегрировав
получим общее решение
и частное (например, положив
При
Отсюда Интегрируя это уравнение получим:
Окончательно получаем общее решение исходного уравнения:
Воспользуемся начальным условием для нахождения требуемого частного решения:
Отсюда
Вопросы для самопроверки 1. Дайте определения дифференциального уравнения и его решения. 2. Что называют общим и частным решением дифференциального уравнения? 3. Какое ДУ называют уравнением с разделяющимися переменными? 4. Какое ДУ 1-го порядка называют линейным? 5. Опишите общую схему метода решения линейного ДУ 1-го порядка. Задачи для самостоятельной работы Найти общее и частное решения дифференциального уравнения первого порядка, используя начальные условия. Таблица 9.
Правила выполнения и оформления контрольной работы 1. Выбор вариантов осуществляется в соответствии с последней цифрой учебного шифра студента (например, если последняя цифра «3», то выполняется вариант номер 3, если - «0», то - вариант номер 10). 2. Контрольная работа пишется чернилами любого цвета (кроме красного) в тонкой тетради, для замечаний рецензента оставляются поля. На обложке тетради указывают фамилию, имя, отчество студента, номер студенческой группы, учебный шифр (серия и номер зачетной книжки), название кафедры, наименование дисциплины и номер контрольной работы, а также домашний адрес. 3. Решение задач следует располагать в порядке следования номеров, указанных в задании, сохраняя номера задач. Условия задач выписывать обязательно. Если несколько задач имеют общую формулировку, то при переписывании общие условия заменяют конкретными данными. 4. Решения задач требуется оформлять аккуратно, подробно объясняя все действия и используемые формулы. В конце работы приводится список использованной литературы, указывается дата выполнения работы и ставится подпись исполнителя. Литература Высшая математика для экономистов. Под ред. Н.Ш. Кремера. М.: Банки и биржи, 1997. Математика: Учебное пособие для экономических специальностей. Под ред. Р.Ш. Марданова, Казань: Изд-во КФЭИ, 1999. Карасев А.И. Курс высшей математики для экономических вузов. М.: Высшая школа, 1982 Кудрявцев В.А. Краткий курс высшей математики. М.: Наука, 1986 Талызин В.А. Контрольная работа по высшей математике. Казань: КИ МГУК, 1998. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
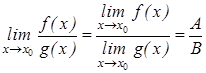 .
.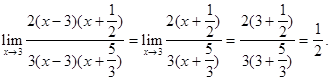
 .
.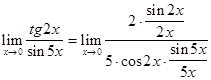 .
. .
.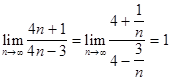 , а
, а  .
.

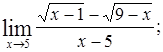





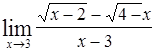
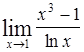
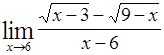

 .
.
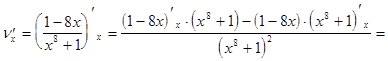
 =
= .
. .
.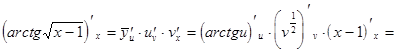

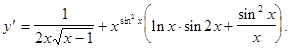
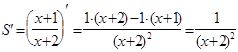 .
. 
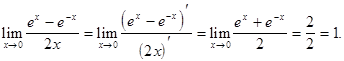

 .
.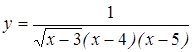



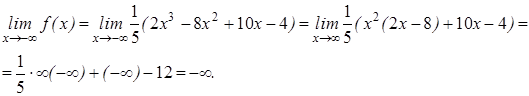
 =0.
=0.
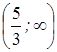 являются интервалами возрастания функции.
являются интервалами возрастания функции.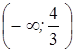 функция вогнута. При
функция вогнута. При  является интервалом выпуклости функции.
является интервалом выпуклости функции. .
.


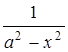

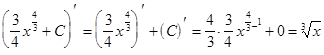 .
.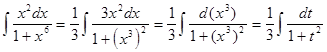
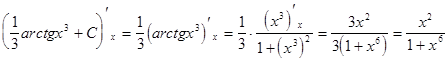 .
.

 .
. .
.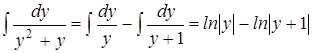 .
.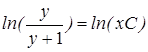 или
или