ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ
Факультет экономики
Кафедра экономического анализа и аудита
Дата регистрации _________________
по дисциплине “Статистика”
На тему (№ варианта) 5
____________________________________________
Студентки(та) ____2____________ курса , группы БАЗ-Д-2С
___________
______________ Шемякина Наталья Степановна _______________________
проживающей(го) по адресу: Кировская область Подосиновский р-н_____
п.Демьяново ул.Советская д.39 кв.134
_______________________________
Преподаватель: ____________Ф., И., О.
__________
Оценка: ____________________________________
Подпись преподавателя: ______________________
Дата проверки: «_____» ________________200__г.
Киров,
2010г.
Задача 2
Имеются следующие данные об объемах производства чугуна в РФ, тыс. т:
| Вид продукции |
1993 |
1994 |
1995 |
Чугун
|
40 519
|
36 116
|
39 229
|
Рассчитайте
относительные величины уровня экономического развития с учетом численности населения РФ, которая составляла (на начало года, млн. чел.): в 1993 г. – 148,7; в 1994 г. – 148,4; в 1995 г. – 148,3 и в 1996 – 148,2.
Сделайте выводы.
Средняя численность населения РФ составила
За 1993г. = 148,7+148,4
=148,55 млн.чел
2
За 1994г. = 148,4+148,3
=148,35 млн.чел
2
За 1995г. = 148,3+148,2
= 148,25 млн.чел
2
Уровень экономического развития составил: в абсолютных величинах
В 1993г. = 40519 тыс.т___
= 0,2728 т на 1 человека
148550 тыс.чел
В 1994г. = 36116 тыс.т___
= 0,2435 т на 1 человека
148350 тыс.чел
В 1995г. = 39229 тыс.т___
= 0,2646 т на 1 человека
148250 тыс.чел
Относительные величины уровня экономического развития в 1994г. По сравнению с 1993г.
0,2435
=0,893∙100%=89,3%
0,2728
Уровень экономического развития в 1994г. по сравнению с 1993г. снизился на 10,7% и составил 89,3%
В 1995г. по сравнению с 1994г.
0,2646
= 1,087∙100% = 108,7%
0,2435
Уровень экономического развития в 1995г. по сравнению с 1994г. вырос на 8,7%
В 1995г. по сравнению с 1993г.
0,2646
=0,970∙100%=97%
0,2728
Уровень экономического развития в 1995г. по сравнению с 1993г снизился на 3% и составил 97%
Задача 13
По двум цехам имеются следующие данные о распределении рабочих по уровню месячной заработной платы за апрель:
| Месячная заработная плата, руб. |
Число рабочих |
| Цех № 1 |
Цех № 2 |
1000 – 1200
1200 – 1400
1400 – 1600
1600 – 1800
1800 – 2000
|
32
36
150
70
32
|
17
40
220
110
83
|
Вычислить по каждому цеху:
1. Средний размер заработной платы рабочих.
Показатели вариации: размах, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.
Сравнить полученные результаты и объяснить причину различия средней заработной платы и показателей вариации. Сделать выводы.
Цех № 1
Средний размер совокупный размер з/платы
з/платы = количество рабочих дней
Средний размер 1100∙32+1300∙36+1500∙150+1700∙70+1900∙32
з/плата = 32+36+150+70+32 = 1521,25 руб.
Показатели вариации:
1. Размах вариации
R= X max-X min
R = 2000-1000= 1000 руб.
2. Среднее линейное отклонение
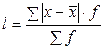 - взвешенное среднее линейное отклонение.
- взвешенное среднее линейное отклонение.
=(1100-1521,25)∙32+(1300-1521,25)∙36+(1500-1521,25)∙150+(1700-1521,25)∙70+(1900-1521,25)∙32
=153,95 руб.
320
3. Диспенсия
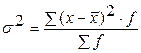 взвешенная дисперсия. взвешенная дисперсия.
= (1100-1521,25)2∙
32+(1300-1521,25)2∙
36+(1500-1521,25)2∙
150+(1700-1521,25)2∙
70+(1900-1521,25)2∙
32
= 44798,44 320
4. Среднее квадратическое отклонение- взвешенное
 = √44798,44=211,66 руб. = √44798,44=211,66 руб.
5. Коэффициент вариации
 = 211,66 ∙
100%=13,91% ‹ 30% = 211,66 ∙
100%=13,91% ‹ 30%
1521,25
Цех № 2
Средний размер совокупный размер з/платы
з/платы = количество рабочих дней
Средний размер 1100∙17+1300∙40+1500∙220+1700∙110+1900∙83
з/плата = 17+40+220+110+83 = 1585,96 руб.
Показатели вариации:
1. Размах вариации
R= X max-X min
R = 2000-1000= 1000 руб.
2. Среднее линейное отклонение
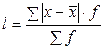 - взвешенное среднее линейное отклонение.=
- взвешенное среднее линейное отклонение.=
(1100-1585,96)∙17+(1300-1585,96)∙40+(1500-1585,96)∙220+(1700-1585,96)∙110+(1900-1585,96)∙83
=164,30 руб.
470
3. Диспенсия
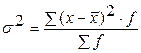 взвешенная дисперсия. взвешенная дисперсия.
=(1100-1585,96)2∙
17+(1300-1585,96)2∙
40+(1500-1585,96)2∙
220+(1700-1585,96)2∙
110+(1900-1585,96)2∙
83
= =43296,99470
4. Среднее квадратическое отклонение- взвешенное
 = √43296,99=208,08 руб. = √43296,99=208,08 руб.
5. Коэффициент вариации
 = 208,08 ∙
100%=13,21% ‹ 30% = 208,08 ∙
100%=13,21% ‹ 30%
1585,96
Выводы: средняя зарплата рабочих цеха № 1 составила 1521,25 руб., цеха № 2 -1585,96 руб. На это повлияло то, что во 2 цехе численность рабочих с наибольшей зарплатой больше. Чем в 1 цехе. Размах зарплаты 1000 руб. Зарплата отдельных работников отклоняется от средней по цеху 1 в среднем на 153,95 руб. (по линейному отклонению) и на 211,66 (по квадратическому отклонению). По 2 цеху на 164,30 руб. (по линейному отклонению) и 208,08 руб. (по квадратическому отклонению). Коэффициенты вариации составили: по цеху № 1-13,91%‹ 30%
по цеху № 2 -13,21% ‹ 30%, что означает, что вариация признаков не значительная, совокупность однородная.
Задача 30
Темпы роста цен на потребительские товары и услуги составили:
| Январь |
Февраль |
Март |
Апрель |
| 1,05 |
1,07 |
1,03 |
1,02 |
Определить:
1. На сколько в среднем за месяц увеличивались цены;
2. Вид средней.
В таблице приведены цепные темпы роста : январь к декабрю
февраль к январю
март к февралю
апрель к марту
Среднемесячный темп роста цен найдем по формуле средней геометрической простой.
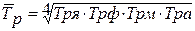 =
=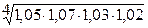 = =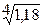 =
1,042∙ 100%=104,2% =
1,042∙ 100%=104,2%
Вывод: в среднем за месяц цены на потребительские товары и услуги увеличились на 4,2%
Вид средней - средняя геометрическая простая
Задача 39
Имеются данные по 10 семьям об уровне доходов на 1 человека в год (х
) и покупательском спросе – расходах на одежду на 1 чел. в год (у
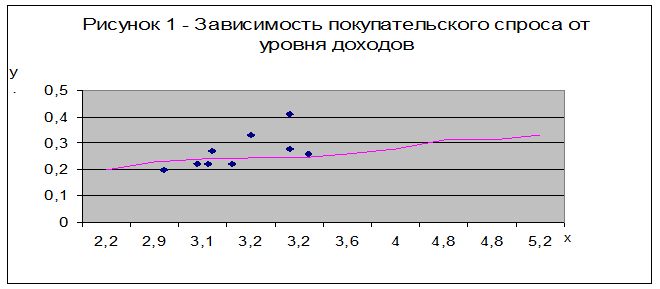
), в млн. руб. Методом корреляционного анализа исследовать зависимость между этими признаками. Написать уравнение регрессии, построить эмпирические точки и линию регрессии. Найти коэффициенты корреляции и детерминации. Сформулировать выводы по результатам анализа.
| х
|
2,9 |
4,8 |
3,2 |
3,2 |
2,2 |
5,2 |
4,0 |
3,1 |
3,6 |
4,8 |
| у
|
0,22 |
0,28 |
0,24 |
0,27 |
0,20 |
0,26 |
0,33 |
0,22 |
0,22 |
0,41 |
Данная связь может быть выражена линейным уравнением регрессии, которое имеет вид:
 =
a
0
+
a
1
x
.
=
a
0
+
a
1
x
.
где  – выровненное значение результативного признака;a
0
– значение y
при х
= 0;
– выровненное значение результативного признака;a
0
– значение y
при х
= 0;
a
1
– коэффициент регрессии (пропорциональности), характеризующий изменение значения y
при изменении х
на 1 единицу.
В данном уравнении два неизвестных параметра a
0
и a
1
, для их нахождения используем метод наименьших квадратов. 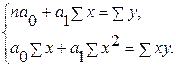 где n
– число уровней (членов) ряда (в нашем примере 10);Σ
x
– сумма значений факторного признака; где n
– число уровней (членов) ряда (в нашем примере 10);Σ
x
– сумма значений факторного признака;
Σ
y
- сумма значений результативного признака;Σ
x
2
- сумма значений квадратов факторного признака;Σ
х
y
- сумма произведений значений факторного признака на значение результативного признака. Чтобы решить данную систему построим вспомогательную таблицу (таблица 2).
Таблица 2 - Расчетная таблица
| x
|
y
|
xy
|
x
2
|
y
2
|
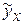 |
 |
| 2,9 |
0,22 |
0,638 |
8,41 |
0,0484 |
0,2307 |
0,00 |
| 4,8 |
0,28 |
1,344 |
23,04 |
0,0784 |
0,3124 |
0,00 |
| 3,2 |
0,24 |
0,768 |
10,24 |
0,0576 |
0,2436 |
0,00 |
| 3,2 |
0,27 |
0,864 |
10,24 |
0,0729 |
0,2436 |
0,00 |
| 2,2 |
0,2 |
0,44 |
4,84 |
0,04 |
0,2006 |
0,00 |
| 5,2 |
0,26 |
1,352 |
27,04 |
0,0676 |
0,3296 |
0,00 |
| 4,0 |
0,33 |
1,32 |
16 |
0,1089 |
0,2780 |
0,00 |
| 3,1 |
0,22 |
0,682 |
9,61 |
0,0484 |
0,2393 |
0,00 |
| 3,6 |
0,22 |
0,792 |
12,96 |
0,0484 |
0,2608 |
0,00 |
| 4,8 |
0,41 |
1,968 |
23,04 |
0,1681 |
0,3124 |
0,01 |
| 37
|
2,65
|
10,168
|
145,42
|
0,7387
|
2,65
|
0,01
|
Полученные в итоговой строке значения подставляем в систему нормальных уравнений и решаем ее.
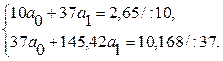
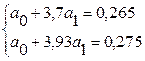
Вычитая из первого уравнения второе получаем:
 , откуда , откуда 
Подставляем числовое значение 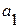 в одно из уравнений (например, в первое) и получаем: в одно из уравнений (например, в первое) и получаем:
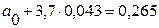 , откуда , откуда  . .
Таким образом, нами получено следующее уравнение корреляции связи или линейное уравнение регрессии:
 =0,106+0,043
x
.
=0,106+0,043
x
.
Коэффициент регрессии a1
показывает, что при увеличении доходов покупательский спрос в среднем возрастает на 0,6 млн. руб.
Если перед коэффициентом a1
знак «-», то тенденция к снижению (связь обратная).
Рассчитаем коэффициент корреляции:
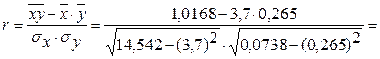  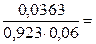
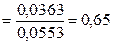
Т.к. r
>
0, то связь между уровнем доходов и покупательском спросе (расходах на одежду) прямая, а т.к. 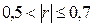 связь умеренная. связь умеренная.
Рассчитаем коэффициент детерминации:
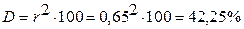 , ,
Коэффициент детерминации показывает, что покупательский спрос (расходы на одежду) зависит на 42,25%от уровня доходов на 1 человека. Остальные 57,75% связаны с другими факторами, которые мы не рассматриваем.
Задача 41
Найти период времени n, за который сумма, положенная на депозит по простой ставке 40% годовых, возрастет в 6 раз.
Предмет и метод статистики финансов
1.Предмет и задачи финансовой статистики.
2.Методы высших финансовых вычислений.
(1). Объектом статистического изучения финансов является образование и использование финансовых ресурсов, кредитное и денежное обращение. В круг решаемых статистикой задач входит:
· разработка методологии и организации статистического наблюдения за финансовыми ресурсами, включая разработку форм отчетности для финансово-кредитных учреждений, предприятий и организаций;
· проведение специальных расчетов;
· выбор методов статистической обработки информации; разработка системы публикаций.
Наиболее важные разделы финансовой статистики: статистика госбюджета; состояние денежно-кредитной сферы; отдельное направление- изучение статистики финансов предприятий.
Основными методами статистики финансов являются методы высших финансовых вычислений.
(2). Начисление простых процентов
.
Процентными деньгами или процентами
называют сумму дохода от предоставления денег в долг в различных формах: открытие депозита, предоставление кредита, покупка облигаций. Сумма процентов зависит от суммы долга, срока его выплаты и процентной ставки, характеризующей интенсивность начисления процентов. Проценты могут выплачиваться по мере их начисления или присоединяться к сумме долга. Увеличение суммы долга за счет присоединения начисленных процентов называется наращением или ростом первоначальной суммы долга.
Отношение наращенной суммы к первоначальной сумме долга называется множителем или коэффициентом наращения
. При использовании простых процентов сумма процентных денег в течение всего периода начисления определяется исходя из первоначальной суммы долга. Процентная ставка
в этих случаях представляет собой выраженное в процентах отношение процентных денег к первоначальной сумме долга:
 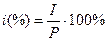 , ,
 где i
- процентная ставка; где i
- процентная ставка;
 I
- сумма процентных денег; I
- сумма процентных денег;
 P
- первоначальная сумма долга. P
- первоначальная сумма долга.
На практике в расчетах процентная ставка принимается как относительное значение в виде коэффициента:  . Из последней формулы следует, что сумма процентных денег равна: . Из последней формулы следует, что сумма процентных денег равна: 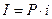 . .
Если период начисления составляет n
-лет, то 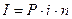 . Общая сумма денег с процентами или наращенная сумма (S
) составляет . Общая сумма денег с процентами или наращенная сумма (S
) составляет 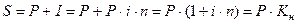 , Kн
-множитель (коэффициент) наращения. , Kн
-множитель (коэффициент) наращения.
Если срок хранения вклада определяется в днях, то вместо n
берем 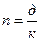 , где д
– количество дней хранения вклада, к
- количество дней в году. , где д
– количество дней хранения вклада, к
- количество дней в году.
В зависимости от сочетания к
и д
на практике встречаются следующие способы расчета:
1)германская практика: количество дней в году принимается равным 360, в месяце –30 дней;
2)французская практика: количество дней в году – 360; в месяце фактическое количество дней;
3)английская практика: количество дней в году и в месяце фактическое.
При этом всегда день открытия вклада и день закрытия считаются за один.
Например, если деньги хранились в банке с 10 сентября по 7 ноября, то число дней хранения вклада по германской практике равно:
д
= 21(сентябрь)+30(октябрь)+7(ноябрь)-1=57 дней.
Использование процентных чисел при определении суммы процентных денег
.
При изменении сумм на счете общая сумма процентов (I
) за весь срок хранения вклада будет равна сумме процентов за каждый период начисления. При этом на практике для начисления процентов применяется методика расчета с применением процентных чисел.
 . .
При необходимости определения суммы процентов все процентные числа складываются и их сумма делится на постоянный делитель (процентный ключ или дивизор):
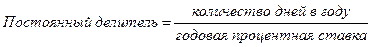 . .
 . .
Если ставки процентов изменяются в течение срока хранения, то сумму процентных денег можно определить: предположим, что на последовательных интервалах времени n1
и n2
процентные ставки i1
и i2
, то суммы процентных денег за каждый период составят I1
=
P
×
i1
×
n1
, I2
=
P
×
i2
×
n2
, а сумма процентных денег за весь срок хранения вклада (n1
+ n2
) определяется следующим образом I=
P
×
i1
×
n1
+ P
×
i2
×
n2
= =P
×
(i1
×
n1
+i2
×
n2
).
Из формулы 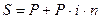 можно вывести: можно вывести:
 ; ;  ; ; 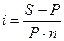 ; ; 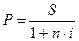 . .
Процесс нахождения первоначальной суммы долга при известных наращениях суммы и процентной ставке называется дисконтированием, а сумма долга современной стоимостью 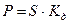 , где , где  . .
|