Лекция №1
Тема: Введение в предмет. Разделы физики. Физические законы и системы единиц. Элементы векторной алгебры. Производная и интеграл при решении физических задач.
Физика – наука о природе. Основные разделы физики:
- Механика – наука о движении. Механика подразделяется на классическую и релятивистскую. В классической механике рассматривается движении с низкими скоростями, а в релятивистской – со скоростями соизмеримыми со скоростями света.
- М.К.Т и термодинамика – рассматривает поведение макросистем, на основе представления о частицах, которые входят в состав рассматриваемых систем.
- Электромагнетизм – рассматривает явления, связанные с взаимодействием электрических зарядов.
- Колебания и волны – рассматривает процессы, повторяющиеся в пространстве с течением времени.
- Оптика – наука о распространении света и его взаимодействия с веществом.
- Квантовая физика – раздел физики, в котором свет рассматривают с корпускулярной точки зрения.
- Атомная и ядерная физика – рассматривает явления, связанные со строением атома и ядра.
Физические законы устанавливаются на основе обобщений неясных фактов и отражают объективные закономерности, существующих в природе. Формулируются физические законы в виде количественным соотношением между физическими величинами.
Основной метод исследования в физике – опыт, то есть наблюдение физического явления в строго контролируемых условиях, позволяющих следить за характером явления и воссоздать его каждый раз при повторении этих условий.
Для объяснения экспериментальных данных выдвигается гипотеза. Правильность выдвинутой гипотезы подтверждается её сопоставлением с результатами эксперимента.
Физическая теория представляет собой систему основных идей, обобщающих опытные данные и отражающих объективные закономерности природы.
Каждая физическая величина имеет единицу измерения. Совокупность единиц измерения составляет систему единиц.
Наиболее распространённая система – интернациональная (СИ), которая строится на семи основных единицах и двух дополнительных: метр, килограмм, секунда, ампер, кельвин, моль, кандела, радиан, стерадиан.
Размерность физической величины есть её выражение в основных единицах.
Основные понятия векторной алгебры.
Вектором называется величина, характеризующаяся численным значением и направлением и складывающаяся по правилу параллелограмма. Модулем вектора называется его численное значение. Модуль вектора – скаляр, причем всегда положительный. Обозначение векторов: 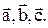
Действие над векторами:
1.
Сложение векторов:
- Правило треугольника. Если начало второго вектора совместить с концом первого, то вектор, проведенный из начала первого в конец второго будет являться суммой двух векторов.
- Правило параллелограмма. Если оба вектора выходят из одной точки, то суммой векторов будет вектор, выходящий из общей точки и совпадающий с диагональю параллелограмма, сторонами которого являются два исходных вектора.
2.
Вычитание векторов: 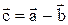 . .
Разностью векторов 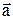 и и 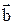 называется вектор называется вектор 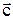 , который в сумме с вектором , который в сумме с вектором 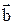 даёт вектор даёт вектор 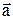 . .
Для нахождения разности двух векторов их необходимо параллельным переносом перенести так, чтобы они выходили из одной точки. Вектор, соединяющий их концы, который направлен в сторону уменьшаемого, называется разностью двух векторов.
3.
Умножение вектора на скаляр: 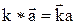 . .
В результате получается новый вектор, длина которого в k раз больше исходного.
4.   Проекция вектора. Проекцией вектора на координатную ось называется произведение модуля вектора на соsугла между направлениями вектора и координатной оси. Проекция вектора. Проекцией вектора на координатную ось называется произведение модуля вектора на соsугла между направлениями вектора и координатной оси.
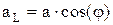
Выражение вектора через его проекции.
Из рисунка следует:
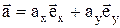
В общем случае, в трёхмерной декартовой системе координат, последнее выражение принимает вид:
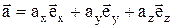
5. Радиус-вектор 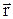 – это вектор, проведённый из начала координат в данную точку. Его проекции на координатные оси равны декартовым координатам данной точки. В декартовой системе координат радиус–вектор можно представить следующим образом: – это вектор, проведённый из начала координат в данную точку. Его проекции на координатные оси равны декартовым координатам данной точки. В декартовой системе координат радиус–вектор можно представить следующим образом:
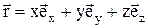
6. Скалярным произведением векторов называется скаляр, равный произведению модулей векторов на 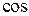 угла между ними. угла между ними.
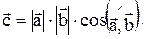
7. Векторным произведением векторов 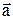 и и  называют вектор называют вектор 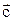 , определяемый по отношению: , определяемый по отношению:
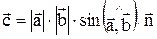
где 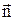 – вектор нормали к плоскости, в которой лежат вектора – вектор нормали к плоскости, в которой лежат вектора 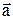 и и  . Направление . Направление 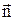 выбирается так, чтобы векторы выбирается так, чтобы векторы 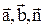 – образовали правовинтовую систему. – образовали правовинтовую систему.
Понятие дифференцирования и интегрирования.
 Пусть функция f(x) возрастает на интервале от x до x+Dx. Пусть функция f(x) возрастает на интервале от x до x+Dx.
Средней скоростью возрастания функции называется отношение изменения функции к изменению аргумента.
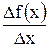 . .
Предел, к которому стремится средняя скорость при приращении аргумента, стремящемся к нулю, называется мгновенной скорости возрастания функции или производной функции в данной точке.
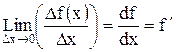
Процесс вычисления производных называется дифференцированием.
Процесс обратный дифференцированию называется интегрированием
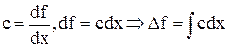 . .
Правило вычисления производных:
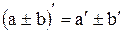
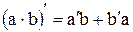
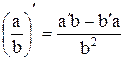
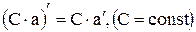
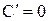
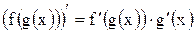
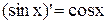
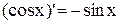
|