Реферат: Анализ САУ с помощью MATLAB и SIMULINK

Анализ САУ с помощью MATLAB и SIMULINK

-Построение временных характеристик с помощью пакета Control System

В качестве примера выберем апериодическое звено первого порядка

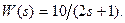
Для построения временных характеристик с помощью пакета Control System используются функции step иimpulse .

Последовательность действий следующая:

1) Задается описание системы:

- в виде передаточной функции с помощью функции tf :

>> sys = tf ([10], [2 1])

Transfer function:

10

(2 s + 1)

Параметрами функции tf являются вектора коэффициентов числителя и знаменателя.

- в виде полюсов, нулей и коэффициента передачи передаточной функции с помощью функции zpk :

>> sys = zpk ([ ], [-0.5], 5)

Zero/pole/gain:

5

( s + 0.5)

Параметрами функции zpk являются вектора нулей, полюсов и коэффициент передачи.

- в пространстве состояний с помощью функции ss :

>> sys = ss ([-0.5], [2], [2.5], [0])

Параметрами функции ss являются матрицы состояния системы A, B, C, D.

2) Строится соответствующая временная характеристика:

- переходная – с помощью функции step :

>> step ( sys )

- импульсная (весовая) – с помощью функции impulse :

>> impulse ( sys )

-Построение переходной характеристики с помощью SIMULINK

Для определения переходной характеристики САУ необходимо в SIMULINK построить модель системы, к входу подключить блок единичного скачка Step , а к выходу – блок осциллографа Scope . При анализе параметров переходного процесса необходимо учитывать, что по умолчанию в блоке Step время скачка – 1 с , а не 0 с .

Импульсную характеристику нельзя получить с помощью SIMULINK, так как блок, формирующий δ-функцию, отсутствует, а его моделирование путем дифференцирования единичного скачка дает большую погрешность.

-Построение частотных характеристик САУ с помощью

пакета Control System

Исходными данными для построения является любое описание системы, применяемые в MATLAB:

- передаточная функция:

>> sys = tf ([10], [2 1])

Transfer function:

10

(2 s + 1)

- полюсы, нули и коэффициент передачи передаточной функции:

>> sys = zpk ([ ], [-0.5], 5)

Zero/pole/gain:

5

( s + 0.5)

- описание в пространстве состояния:

>> sys = ss ([-0.5], [2], [2.5], [0])

- описание в виде модели SIMULINK.

Логарифмическая амплитудная и фазовая частотные характеристики строятся в Control System с помощью функции bode:

>> bode ( sys)

В качестве параметра задается имя описания системы (передаточной функции). При этом диапазон частот для построения графиков выбирается автоматически. Если выбранный диапазон частот не удовлетворяет поставленным требованиям, его можно задать (0.01…1000 Гц):

>> bode ( sys, (0.01 1000))

Амплитудно-фазовая частотная характеристика (АФЧХ) строится с помощью функции nyquist:

>> nyquist ( sys)

или, для требуемого диапазона частот

>> nyquist ( sys, (0.01 1000))

Следует отметить, что АФЧХ строится как для положительных, так и для отрицательных частот.

-Преобразование модели SIMULINK в модель Control System MATLAB

Модель в виде структурной схемы в SIMULINK является более простым и наглядным представлением системы, чем в виде передаточных функций в Control System . В тоже время Control System представляет широкие возможности по анализу САУ. Поэтому часто возникает задача преобразования структурной схемы SIMULINK в модель Control System . Рассмотрим алгоритм такого преобразования.

1) Создание структурной схемы в SIMULINK.Рекомендуется сначала создать схему для моделирования, затем преобразовать ее в схему для анализа. Для этого необходимо отключить задающее воздействие, к входу системы подключить входной порт, а к выходу – выходной порт (блоки In ; Out ); разорвать главную обратную связь при анализе устойчивости.

Рис. 4.2. Исходная модель

Рис. 4.3. Преобразованная модель

2) Извлечение информации из модели :

>> [A,B,C,D ] = linmod (‘untitled’)

A =

-0.5000

B =

1

C =

5

D =

0

С использованием функции linmod получается описание модели в пространстве состояний с помощью матриц состояния A , B , C , D . В качестве параметра функции linmod указывается имя модели (оно указано в заголовке окна модели).

3) Преобразование матриц состояния в модель Control System :

<< sys = ss (A,B,C,D )

a =

x1

x1 -0.5

b =

u1

x1 1

c =

x1

y1 5

d =

u1

y1 0

Continuous – time mode1.

Параметрами функции ss являются матрицы состояния; sys – имя получаемой модели.

Полученная модель может использоваться для построения временных и частотных характеристик динамических системы:

<< step ( sys ) ;grid (grid – отображение сетки графика);

<< impulse(sys) ; grid

<< bode(sys) ; grid

<< nyquist(sys) ; grid

Литература

1. Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и моделирование систем. Специальный справочник. – СПб.: Питер,

2002. – 448с.

2. Дьяконов В. П. Справочник по применение системы PCMATLAB. – М.: Наука, Физматлит, 1993.

3. Дьяконов В. П. Компьютерная математика. Теория и практика. – М.: Нолидж, 2001.

4. Дьяконов В., Новиков Ю., Рычков В. Компьютер для студента; Самоучитель. – СПб: Питер, 2000.

5. Потемкин В. Г. MATLAB. Справочное пособие. - М.: ДИАЛОГ-МИФИ, 1997.

6.Потемкин В. Г. MATLAB 5 для студентов. - М.: ДИАЛОГ-МИФИ, 1998.

7. Потемкин В. Г. Система инженерных и научных расчетов

MATLAB 5.x. Том 1 и 2..- М.: ДИАЛОГ-МИФИ, 1999.

8. Дьяконов В. П., Абраменкова И. В. MATLAB 5. Система символьной математики. – М.: Нолидж, 1999.

9. Дьяконов В. П. MATLAB. Учебный курс. – СПб: Питер, 2000.

10. Дьяконов В. П., Абраменкова И. В., Круглов В. В. MATLAB 5.3.1 с пакетами расширений. – М.: Нолидж, 2001.