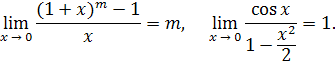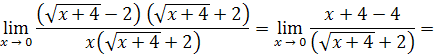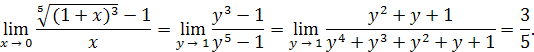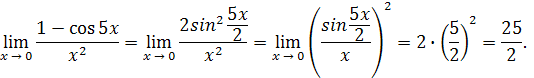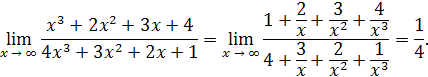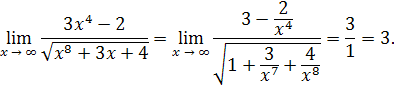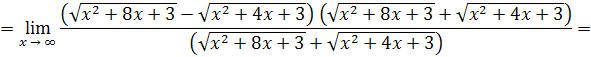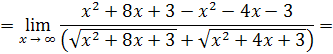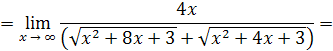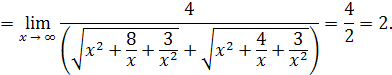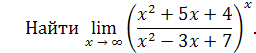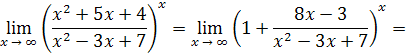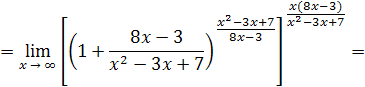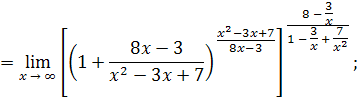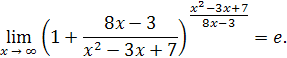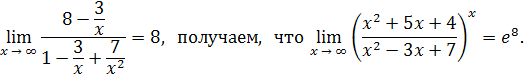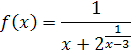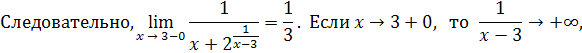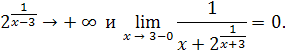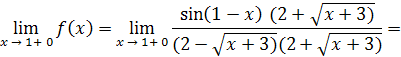Книга: Введение в математический анализ
|
Название: Введение в математический анализ Раздел: Рефераты по математике Тип: книга |
Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственный технический университет ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ Учебное пособие по математике для студентов всех специальностей заочной формы обучения 2007 ФУНКЦИЯ ОДНОЙ НЕЗАВИСИМОЙ ПЕРЕМЕННОЙ Основные определения и понятия Одним из основных понятий математики является число. Числа целые и дробные, как положительные, так и отрицательные, вместе с числом ноль называются рациональными числами. Рациональные числа могут быть представлены в виде конечных или бесконечных периодических дробей. Числа, которые представляются в виде бесконечных, но непериодических дробей, называются иррациональными . Совокупность всех рациональных и иррациональных чисел называется множеством действительных , или вещественных чисел. Действительные числа можно изображать точками числовой оси. Числовой осью называется бесконечная прямая, на которой выбраны: 1) некоторая точка О, называемая началом отсчёта; 2) положительное направление, указываемое стрелкой; 3) масштаб для измерения длин. Между всеми действительными числами и всеми точками числовой оси существует взаимно–однозначное соответствие , т.е. каждому действительному числу соответствует точка числовой оси и наоборот. Абсолютной величиной (или модулем ) действительного числа x называется неотрицательное действительное число ׀x ׀, определяемое следующим образом: ׀x ׀ = x , если x ≥ 0, и ׀x ׀ = –x , если x < 0. Переменной величиной называется величина, которая принимает различные численные значения. Величина, численные значения которой не меняются, называется постоянной величиной. Переменная величина называется упорядоченной
, если известна область её изменения и про каждое из двух любых её значений можно сказать, какое из них предыдущее и какое последующее. Частным случаем такой величины является числовая последовательность Переменная величина называется возрастающей (убывающей ), если каждое её последующее значение больше (меньше) предыдущего. Возрастающие и убывающие переменные величины называются монотонными . Переменная величина называется ограниченной , если существует такое постоянное число M > 0, что все последующие значения переменной, начиная с некоторого, удовлетворяют условию: – M ≤ x ≤ M, т.е. ׀x ׀ ≤ M. Переменная величина y называется (однозначной) функцией переменной величины x, если каждому значению переменной величины x, принадлежащему множеству действительных чисел X, соответствует одно определённое действительное значение переменной величины y . Переменная x называется в этом случае аргументом , или независимой переменной , а множество X – областью определения функции. Запись y = f ( x ) означает, что y является функцией x . Значение функции f ( x ) при x = a обозначают через f ( a ). Область определения функции в простейших случаях представляет собой: интервал
(открытый промежуток
) (a
,
b
), т.е. совокупность значений x
, удовлетворяющих условию a
<
x
<
b
; сегмент
(отрезок
или замкнутый
промежуток
) Графиком функции y = f ( x ) называется геометрическое место точек плоскости xOy, координаты которых удовлетворяют уравнению y = f ( x ). Функция f
(
x
)
называется чётной, если Функция f
(
x
)
называется периодической
, если существует такое положительное число T, называемое периодом
функции, что для любого значения x
выполняется равенство Наименьшим же периодом функции называется наименьшее положительное число τ, для которого f ( x + τ) = f ( x ) при любом x . Следует иметь в виду, что f ( x + k τ) = f ( x ) , где k – любое целое число. Функции задаются: 1) аналитически (в виде формулы), например, 2) графически (в виде графика); 3) таблично (в виде таблицы), например таблица логарифмов. Основными элементарными функциями являются следующие, аналитически заданные функции: 1. Степенная функция
: 2. Показательная функция
: 3. Логарифмическая функция
: 4. Тригонометрические функции : y = sinx , y = cosx , y = tgx , y = ctgx , y = sec x, y = cosec x. 5. Обратные тригонометрические функции : y = arcsin x, y = arccos x, y = arctg x, y = arcctg x, y = arcsec x , y = arccosecx . Если y является функцией от u
, а u
есть функция от x
, то y также зависит от x
. Пусть y
= F(u
), u
= φ(x
). Тогда y
= F(φ(x
)). Последняя функция называется функцией от функции
, или сложной функцией.
Например, y
= sinu
, u
= Элементарной функцией называется функция, которая может быть задана одной формулой вида y = f ( x ) , где выражение f ( x ) составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции. Например, y
= ׀x
׀ = Пример 1
. Найти Решение . Найдём значения данной функции при x = a и x = b :
Тогда получим
Пример 2 . Определить, какая из данных функций чётная или нечётная: а) г) Решение
. а) Так как
б) Имеем f(– x) = f(x). Следовательно, функция чётная. в) Здесь f (– x ) = f ( x ). Следовательно, функция чётная. г) Здесь Пример 3
. Найти область определения функции Решение
. Функция Пример 4
. Найти область определения функции Решение . Функция определена, если x – 1 ≠ 0 и 1+ x > 0, т.е. если x ≠ 1 и x > – 1. Область определения функции есть совокупность двух интервалов: ( – 1, 1) и (1, + ∞). Пример 5. Найти область определения функции
Решение.
Первое слагаемое
ПОСТРОЕНИЕ ГРАФИКОВ ФУНКЦИЙ При построении графиков функций применяются следующие приёмы: а) построение «по точкам»; б) действия с графиками (сложение, вычитание, умножение графиков); в) преобразования графиков (сдвиг, растяжение). Исходя из графика функции y = f ( x ) , можно построить графики функций: 1) y = f (x – a ) – первоначальный график, сдвинутый вдоль оси Оx на величину a ; 2) y = f (x ) + b – тот же график, сдвинутый вдоль оси Oy на величину b ; 3) y = A · f (x ) – исходный график, растянутый в A раз вдоль оси Oy; 4) y = f (kx ) – тот же график, сжатый в k раз вдоль оси Ox. Таким образом, можно по графику функции y
=
f
(x
) построить график функции вида
Рис. 1 Пример 6 . Построить график функции y = 2x + 1 + cosx . Решение . График данной функции можно построить путём сложения графиков двух функций: y = 2x + 1, y = cosx . График первой функции есть прямая, её можно построить по двум точкам, график второй функции–косинусоида(Рис. 1). Пример 7
. Построить график функции Решение . При x < 3 графиком является луч прямой, а при x ≥ 3 – ветвь параболы. Искомый график изображен на рис. 2.
Рис. 2 Пример 8
. Построить график функции y
= 2 sin (2x
– 1) или Решение
. Здесь
Рис.3 ПРЕДЕЛЫ Число а
называется пределом последовательности
Число A называется пределом функции
f(x) при x → a
, если для любого сколь угодно малого ε > 0 найдётся такое δ > 0, что ׀f
(
x
)
– A׀ < ε при
где M – произвольное положительное число . В этом случае функция f ( x ) называется бесконечно большой величиной при x → a .
Если x < a и x → a , то условно пишут x → a – 0; если x > a и x → a , то пишут x → a + 0.
делом функции f (x ) в точке a .
Практическое вычисление пределов основывается на следующих теоремах.
4) 5) Используются также первый и второй замечательные пределы: 1) 2) Логарифм числа x по основанию e называется натуральным логарифмом и обозначается lnx . При решении примеров полезно иметь в виду следующие равенства:
Пример 9
. Показать, что при n
→∞ последовательность Решение
. Здесь n
–й член последовательности Пример 10 . Показать, что при n → ∞ последовательность 7/3, 10/5, 13/7, . . . , (3n + 4) /(2n + 1), . . . имеет пределом число 3/2. Решение
. Здесь 5/ Положив ε = 0,1, заключаем, что неравенство Неравенство Неравенство Пример 11 .
Решение . Так как x → 4, то числитель дроби стремится к числу 5 · 4 + 2 = 22, а знаменатель к числу 2 · 4 + 3 = 11.
Пример 12 .
Решение. Числитель и знаменатель дроби безгранично возрастают при x
→ ∞. В таком случае говорят, что здесь имеет место неопределённость вида Разделив на x числитель и знаменатель дроби, получаем
Пример 13 .
Решение . Здесь числитель и знаменатель дроби стремятся к нулю при x
→ 3 (принято говорить, что получается неопределённость вида
Пример 14 .
Решение . Разложим на множители числитель и знаменатель дроби:
Пример 15 .
Решение . Имеем
Числитель дроби стремится к 300, а знаменатель стремится к нулю, т.е. является бесконечно малой величиной, следовательно, рассматриваемая дробь –бесконечно большая величина и
Пример 16 .
Решение . Умножим числитель и знаменатель дроби на сумму
Пример 17 .
Решение
. Положим
Пример 18 .
Решение . Имеем
Пример 19 .
Решение . Имеем
Здесь мы воспользовались результатом предыдущего примера, приняв
Пример 20 .
Решение
. Разделим числитель и знаменатель дроби на старшую степень x
, т.е. на
Пример 21 .
Решение
. Разделим числитель и знаменатель на
Пример 22 .
Решение . Умножим и разделим рассматриваемое выражение на
Пример 23.
Решение . Делением числителя дроби на знаменатель выделим целую часть:
Таким образом,
так как
то
Приняв во внимание, что
Пример 24 . Найти левый и правый пределы функции
при x → 3. Решение .
Пример 25
. Найти левый и правый пределы функции x → a . Решение .
НЕПРЕРЫВНОСТЬ ФУНКЦИИ Функция f(x) называется непрерывной в точке а
, если: 1) эта функция определена в некоторой окрестности точки а
; 2) существует
Обозначая
тогда, когда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. Если функция непрерывна в каждой точке некоторой области (интервала, сегмента и т.п.), то она называется непрерывной в этой области . Точка а , принадлежащая области определения функции или являющаяся граничной для этой области, называется точкой разрыва , если в этой точке нарушается условие непрерывности функции. Если существуют конечные пределы:
причём не все три числа В частности, если левый и правый пределы функции в точке а
равны между собой: Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода . В точках разрыва II рода не существует хотя бы один из односторонних пределов. Сумма и произведение конечного числа непрерывных функций есть функция непрерывная. Частное от деления двух непрерывных функций есть функция непрерывная во всех точках, где делитель не равен нулю. Пример 26 .
Решение . Находим
Таким образом, функция при Пример 27 .
Решение .
Итак, при
Рис. 4 Рис. 5 Разность между правым и левым пределом в точке разрыва I рода
(рис. 5). Пример 28 .
Решение
. В точке
может быть сокращена на
Таким образом, при
Пример 29
. Доказать, что функция Решение
. Находим
Значит, функция Пример 30 . Исследовать на непрерывность функцию
и изобразить график функции в окрестностях точки разрыва. Решение
. Знаменатель Для определения типа разрыва надо найти пределы функции слева и справа при
Таким образом, пределы функции слева и справа при
Рис. 6 Доопределив функцию
|



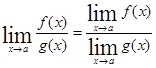 при (
при (