Лекция: Термодинамическое равновесие и устойчивость. Фазовые переходы.
План:
1. Экстремальные свойства термодинамических потенциалов.
2. Условия равновесия и устойчивости пространственно однородной системы.
3. Общие условия равновесия фаз в термодинамических системах.
4. Фазовые переходы I-го рода.
5. Фазовые переходы II-го рода.
6. Обобщение полуфеноменологической теории.
Вопросы устойчивости термодинамических систем рассматривались в предыдущей теме применительно к задаче химического равновесия. Поставим задачу теоретического обоснования сформулированных ранее условий (3.53) на основе II начала термодинамики, используя свойства термодинамических потенциалов.
Рассмотрим макроскопическое бесконечно малое изменение состояния системы: 1 -2, при котором все ее параметры относятся на бесконечно малую величину:
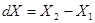 (4.1) (4.1)
Соответственно:
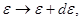 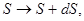  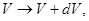 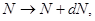 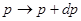 и т.д. и т.д.
Тогда в случае квазистатического перехода из обобщенной формулировки I и II начала термодинамики (2.16) следует:
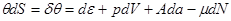 (4.2) (4.2)
В случае, если 1-2 является неквазистатическим, то выполняются следующие неравенства:
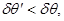 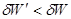 (4.3) (4.3)
В выражении (4.3) величины со штрихом соответствуют неквазистатическому процессу, а величины без штриха – квазистатическому. Первое неравенство системы (4.3) характеризует полученный на основе обобщения многочисленных опытных данных принцип максимального поглощения тепла, а второе – принцип максимальной работы.
Записывая работу для неквазистатического процесса в виде  и вводя аналогичным образом параметры и вводя аналогичным образом параметры 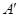 и и 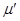 , получим: , получим:
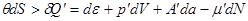 (4.4) (4.4)
Выражение (4.4) абсолютно эквивалентно неравенству Клаузиуса.
Рассмотрим основные следствия (4.4) для различных способов описания термодинамических систем:
1. Адиабатически изолированная система: (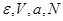 ). Соответственно ). Соответственно 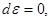 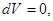 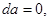  . Тогда: . Тогда:
 (4.5) (4.5)
Это означает, что если зафиксировать переменные состояния системы, то вследствие (4.5) ее энтропия будет возникать до тех пор, пока в системе, согласно нулевого начала термодинамики, не наступит состояния равновесия. То есть равновесия состояния соответствует максимуму энтропии:
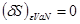 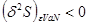 (4.6) (4.6)
Вариации в (4.6) производятся по тем параметрам, которые при указанных фиксированных параметрах системы могут принимать неравновесные значения. Это могут быть концентрация п
, давление р
, температура  ит.д. ит.д.
2. Система в термостате (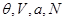 ). Соответственно ). Соответственно 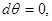 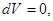 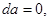  что позволяет переписать (4.4) в виде: что позволяет переписать (4.4) в виде:
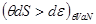 (4.7) (4.7)
Учитывая вид выражения для свободной энергии: 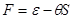 и равенство и равенство 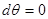 , получаем: , получаем:
 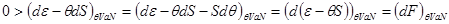 (4.8) (4.8)
Таким образом течение неравновесных процессов для системы, помещенной в термостат, сопровождается уменьшением ее свободной энергии. А равновесное значенте соответствует ее минимуму:
 , ,
то есть
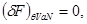 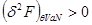 (4.8) (4.8)
3. Система под поршнем (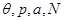 ), т.е. ), т.е. 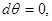  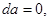  .В этом случае соотношение (4.4) принимает вид: .В этом случае соотношение (4.4) принимает вид:
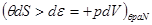 , ,
откуда:
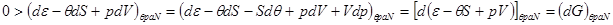 (4.9) (4.9)
Таким образом равновесие в системе под поршнем наступает при достижении минимального значения потенциала Гиббса:
 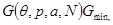  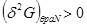 (4.10) (4.10)
4. Система с воображаемыми стенками (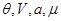 ). Тогда ). Тогда 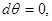 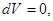 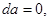 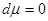 . Тогда . Тогда
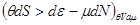 , ,
что позволяет записать
 (4.11) (4.11)
Соответственно в системе с воображаемыми стенками неравновесные процессы направлены в сторону уменьшения потенциала 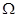 , а равновесие достигается при условии: , а равновесие достигается при условии:
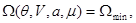 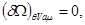 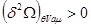 (4.12) (4.12)
Условие 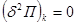 определяет само состояние равновесия системы и широко используется при исследовании многокомпонентных или многофазных систем. Условия минимума определяет само состояние равновесия системы и широко используется при исследовании многокомпонентных или многофазных систем. Условия минимума 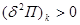 или максимума или максимума 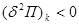 определяют критерии устойчивости этих равновесных состояний по отношению к самопроизвольным или искусственно создаваемым возмущениям системы. определяют критерии устойчивости этих равновесных состояний по отношению к самопроизвольным или искусственно создаваемым возмущениям системы.
Кроме того, наличие экстремальных свойств у термодинамических потенциалов позволяет использовать для их исследования вариационных методов по аналогии с вариационными принципами механики. Однако, в этих целях требуется использование статистического подхода.
2.
Рассмотрим условия равновесия и устойчивости термодинамических систем на примере газа, помещенного в цилиндр над поршнем. Кроме того, для упрощения анализа пренебрежем внешними полями, полагая 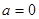 . Тогда переменными состояния являются ( . Тогда переменными состояния являются (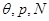 ). ).
Ранее отмечалось, что на термодинамическую систему можно оказывать воздействия либо совершая работу над ней, либо сообщая ей некоторое количество тепла. Поэтому следует проанализировать равновесие и устойчивость по отношению к каждому из отмеченных воздействий.
Механическое воздействие связано со смещением незакрепленного поршня. В этом случае работа на систему равно
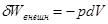
В качестве внутреннего параметра, который может изменяться и по которому следует осуществлять варьирование, выберем объем.
Представляя потенциал Гиббса через свободную энергию
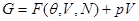
и производя варьирование, запишем:
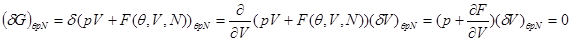
Из последнего равенства следует:
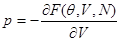 (4.13) (4.13)
Выражение (4.13) следует рассматривать как уравнение относительно равновесного значения объема  при заданных параметрах системы ( при заданных параметрах системы (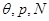 ). ).
Условия устойчивости равновесного состояния имеет вид:
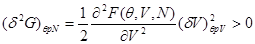
Учитывая (4.13), последнее условие можно переписать в виде:
 (4.14) (4.14)
Условие (4.14) накладывает определенные требования на уравнение состояния 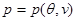 . Так, изотермы идеального газа . Так, изотермы идеального газа
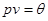
всюду удовлетворяют условию устойчивости. В то же время, уравнение Ван-дер-Ваальса
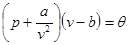 (4.15) (4.15)
или уравнения Дитериги
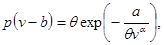 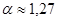 (4.16) (4.16)
имеют участки на которых условия устойчивости не выполняются, и которые не соответствуют реальным равновесным состояниям, т.е. экспериментально реализуется.
Если же в некоторой точке изотермы 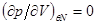 , то для проверки устойчивости используют специальные методы математического анализа, т.е. проверяют выполнение условий: , то для проверки устойчивости используют специальные методы математического анализа, т.е. проверяют выполнение условий:
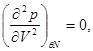 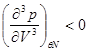 (4.17) (4.17)
Аналогичным образом требования устойчивости, предъявляемые к уравнению состояния, могут быть сформулированы и для других параметров системы. Рассмотрим в качестве примера зависимость химического потенциала. Введем плотность числа частиц 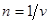 . Тогда химический потенциал можно представить в виде . Тогда химический потенциал можно представить в виде 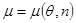 . .
Вычислим дифференциал 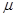 в зависимости от переменных состояния в зависимости от переменных состояния 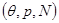 : :
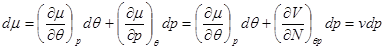
При записи последнего выражения учтено, что 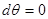 и использовано термодинамическое тождество (3.8). Тогда и использовано термодинамическое тождество (3.8). Тогда
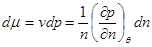 . (4.18) . (4.18)
То есть условие устойчивости 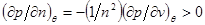 для химического потенциала принимает вид для химического потенциала принимает вид
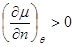 (4.19) (4.19)
В критической точке при наличии прогиба имеем:
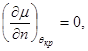 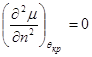 , , 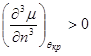 (4.20) (4.20)
Перейдем к анализу устойчивости системы к тепловому воздействию, связанного с передачей некоторого количества тепла 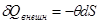 . Тогда в качестве вариационного параметра рассмотрим энтропию системы S
. Для учета именно теплового воздействия зафиксируем механические параметры. Тогда в качестве переменных термодинамического состояния удобно выбрать набор . Тогда в качестве вариационного параметра рассмотрим энтропию системы S
. Для учета именно теплового воздействия зафиксируем механические параметры. Тогда в качестве переменных термодинамического состояния удобно выбрать набор 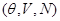 , а в качестве термодинамического потенциала свободную энергию , а в качестве термодинамического потенциала свободную энергию 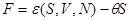 . .
Выполняя варьирование, находим:
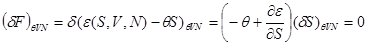
Из условия равновесия 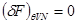 получаем получаем
 (4.21) (4.21)
Уравнения (4.21) следует рассматривать как уравнение для равновесного значения энтропии 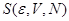 . Из положительности второй вариации свободной энергии: . Из положительности второй вариации свободной энергии:
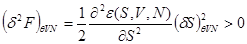
следует:
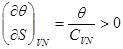 (4.22) (4.22)
Поскольку температура всегда принимает положительные значения из (4.22) следует:
 (4.23) (4.23)
Выражение (4.23) является искомым условием устойчивости термодинамической системы по отношению к нагреванию. Некоторые авторы рассматривают положительность теплоемкости  как одно из проявлений принципа Ле-Шателье – Брауна. При сообщении термодинамической системе количества тепла как одно из проявлений принципа Ле-Шателье – Брауна. При сообщении термодинамической системе количества тепла 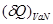 : :
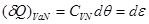 , ,
Ее температура возникает, что, в соответствии со вторым началом термодинамики в формулировке Клаузиуса (1850г.), приводит к уменьшению количества теплоты, поступающего в систему. Иначе говоря, в ответ на внешние воздействия – сообщение количества теплоты – термодинамические параметры системы (температура  ) меняются таким образом, что внешние воздействия ослабляются. ) меняются таким образом, что внешние воздействия ослабляются.
3.
Рассмотрим вначале однокомпонентную систему, находящуюся в двухфазном состоянии. Здесь и далее под фазой будем понимать однородное вещество в химическом и физическом отношении.
Таким образом, каждую фазу будем рассматривать как однородную и термодинамически устойчивую подсистему, характеризуемую общим значением давления (в соответствии с требованием отсутствия тепловых потоков). Исследуем условие равновесия двуфазной системы по отношению к изменению числа частиц 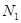 и и 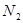 , находящихся в каждой из фаз. , находящихся в каждой из фаз.
С учетом сделанных допущений наиболее удобным является использование описания системы под поршнем с фиксацией параметров (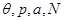 ). Здесь ). Здесь 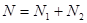 - общее число частиц в обеих фазах. Также для простоты “выключим” внешние поля (а
=0). - общее число частиц в обеих фазах. Также для простоты “выключим” внешние поля (а
=0).
В соответствии с выбранным способом описания условием равновесия является условие (4.10) минимума потенциала Гиббса:
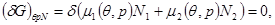 (4.24а) (4.24а)
которое дополняется условием постоянства числа частиц N
:
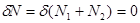 (4.24б) (4.24б)
Выполняя варьирование в (4.24а) с учетом (4.24б) находим:
 
 (4.25) (4.25)
Таким образом, общим критерием равновесия двуфазной системы является равенство их химических потенциалов.
Еси известны выражения химических потенциалов 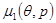 и и 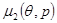 , то решением уравнения (4.25) будет некоторая кривая , то решением уравнения (4.25) будет некоторая кривая
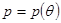 , ,
называемая кривой фазового равновесия или дискретной фазового равновесия.
Зная выражения для химических потенциалов, из равенства (2.юю):

мы можем найти удельные объемы для каждой из фаз:
 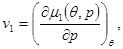  (4.26) (4.26)
То есть, (4.26) можно переписать в виде уравнений состояния для каждой из фаз:
 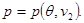 (4.27) (4.27)
Обобщим полученные результаты на случай n
фаз и k
химически нереагирующих компонент. Для произвольной i
-й компоненты уравнение (4.25) примет вид:
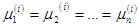 (4.28) (4.28)
Легко видеть, что выражение (4.28) представляет систему (n
-
1) независимых уравнений. Соответственно из условий равновесия для k
компонент получаем k
(n
-1) независимых уравнений (k
(n
-1) связей).
Состояние термодинамической системы в этом случае задается температурой  , давлением p
и k
-1 значениями относительных концентраций компонент в каждой фазе. Таким образом состояние системы в целом задается , давлением p
и k
-1 значениями относительных концентраций компонент в каждой фазе. Таким образом состояние системы в целом задается 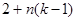 параметром. параметром.
Учитывая 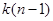 наложенных связей, найдем число независимых параметров системы (степенной свободы). наложенных связей, найдем число независимых параметров системы (степенной свободы).
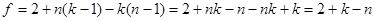 . (4.29) . (4.29)
Равенство (4.29) называют правилом фаз Гиббса.
Для однокомпонентной системы (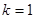 ) в случае двух фаз ( ) в случае двух фаз ( ) имеется одна степень свободы, т.е. мы произвольно можем изменять только один параметр. В случае же трех фаз ( ) имеется одна степень свободы, т.е. мы произвольно можем изменять только один параметр. В случае же трех фаз ( ) не имеется степеней свободы ( ) не имеется степеней свободы (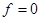 ), то есть сосуществование трех фаз в однокомпонентной системе возможно только в одной точке, называемой тройной точкой. Для воды тройная точка соответствует следующим значениям: ), то есть сосуществование трех фаз в однокомпонентной системе возможно только в одной точке, называемой тройной точкой. Для воды тройная точка соответствует следующим значениям: 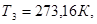  . .
Если система не однокомпонентна, возможны боле сложные случаи. Так, двуфазная ( ) двукомпонентная система ( ) двукомпонентная система (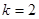 ) обладает двумя степенями свободы. В этом случае вместо кривой фазового равновесия получим область в виде полосы, границы которой соответствуют фазовым диаграммам для каждой из чистых компонент, а внутренние области соответствуют различным значениям относительной концентрации компонент. Одна степень свободы в данном случае соответствует кривой сосуществования трех фаз, а ) обладает двумя степенями свободы. В этом случае вместо кривой фазового равновесия получим область в виде полосы, границы которой соответствуют фазовым диаграммам для каждой из чистых компонент, а внутренние области соответствуют различным значениям относительной концентрации компонент. Одна степень свободы в данном случае соответствует кривой сосуществования трех фаз, а 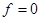 соответствует четвертой точке сосуществования четырех фаз. соответствует четвертой точке сосуществования четырех фаз.
4.
Как было рассмотрено выше, химический потенциал можно представить в виде:
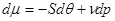
Соответственно первые производные от химического потенциала равны удельным значениям энтропии, взятой с обратным знаком, и объеме:
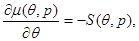 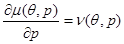 (4.30) (4.30)
Если в точках, удовлетворяющих фазовому равновесию:
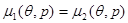 , ,
первые производные химического потенциала для разных фаз испытывают разрыв:
 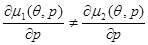 , (4.31) , (4.31)
говорят, что термодинамическая система испытывает фазовый переход I-го рода.
Для фазовых переходов первого рода характерно наличие срытой теплоты фазового перехода, отличной от нуля, и скачок удельных объемов системы. Скрытая удельная теплота фазового перехода определяется из соотношения:
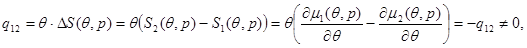 (4.32) (4.32)
а скачок удельного объема равен:
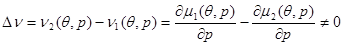 (4.33) (4.33)
Примерами фазовых переходов первого рода являются процессы кипения и испарения жидкостей. Плавления твердых тел, преобразования кристаллической структуры и т.д.
Рассмотрим две близлежащие точки на кривой фазового равновесия (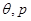 ) и ( ) и ( ), параметры которых различаются на бесконечно малые величины. Тогда уравнение (4.25) справедливо и для дифференциалов химических потенциалов: ), параметры которых различаются на бесконечно малые величины. Тогда уравнение (4.25) справедливо и для дифференциалов химических потенциалов:
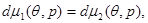
отсюда следует:
 (4.34) (4.34)
Выполняя преобразования в (4.34), получим:
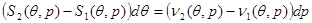
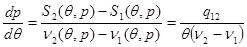 (4.35) (4.35)
Выражение (4.35) получило название уравнения Клапейрона – Клаузиуса. Это уравнение позволяет получить вид кривой фазового равновесия по известным из эксперимента значениям теплоты фазового перехода 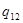 и объемов фаз и объемов фаз 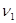 и и 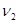 без привлечения понятия химического потенциала, которое достаточно сложно определить как теоретически, так и экспериментально. без привлечения понятия химического потенциала, которое достаточно сложно определить как теоретически, так и экспериментально.
Большой практический интерес представляют так называемые метастабильные состояния. В этих состояниях одна фаза продолжает существовать в области устойчивости другой фазы:

Примерами достаточно устойчивых метастабильных состояний являются алмазы, аморфное стекло (наряду с кристаллическим горным хрусталем) и т.д. В природе и промышленных установках широко известны метастабильные состояния воды: перегретая жидкость и переохлажденный пар, а также переохлажденная жидкость.
Важным обстоятельством является то, что условием экспериментального осуществления этих состояний является отсутствие в системе новой фазы, примесей, загрязнений и т.д., т.е. отсутствие центра конденсации, парообразования и кристаллизации. Во всех этих случаях новая фаза возникает первоначально в малых количествах (капли, пузыри или кристаллы). Поэтому существенными становятся поверхностные эффекты, соизмеримые с объемными.
Для простоты ограничимся рассмотрением простейшего случая сосуществования двух пространственно неупорядоченных фазовых состояний - жидкости и пара. Рассмотрим жидкость, в которой находится небольшой пузырек насыщенного пара. При этом вдоль поверхности раздела действует сила поверхностного натяжения. Для ее учета введем параметры:
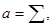  (4.36) (4.36)
Здесь 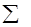 - площадь поверхности пленки, - площадь поверхности пленки, 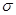
- коэффициент поверхностного натяжения. Знак “-” во втором равенстве (4.36) соответствует тому, что пленка стягивается и работа внешней силы направлена на увеличение поверхности:
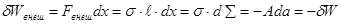 (4.37) (4.37)
Тогда с учетом поверхностного натяжения потенциал Гиббса изменится на величину:

Вводя модель системы под поршнем и, учитывая равенство 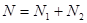 , запишем выражение для потенциала Гиббса в виде , запишем выражение для потенциала Гиббса в виде
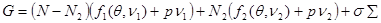 (4.39) (4.39)
Здесь 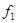 и и 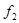 - удельные значения свободной энергии, - удельные значения свободной энергии, 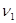 и и 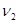 - удельные объемы каждой из фаз. При фиксированных значениях ( - удельные объемы каждой из фаз. При фиксированных значениях (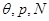 ) величина (4.39) достигает минимума. При этом потенциал Гиббса можно проварьировать по ) величина (4.39) достигает минимума. При этом потенциал Гиббса можно проварьировать по 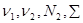 . Эти величины связаны с помощью соотношения: . Эти величины связаны с помощью соотношения:
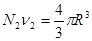 , ,
где R
можно выразить через 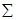 : :  . Выберем в качестве независимых параметров величины . Выберем в качестве независимых параметров величины 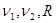 , тогда потенциал Гиббса (4.39) можно переписать в виде: , тогда потенциал Гиббса (4.39) можно переписать в виде:
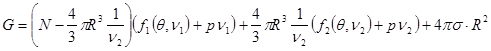 (4.46) (4.46)
(здесь учтено 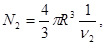  ) )
Выполняя варьирование (4.40), запишем:
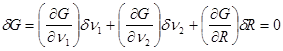 (4.47) (4.47)
Учитывая независимость величин 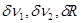 , сведем (4.41) к системе , сведем (4.41) к системе
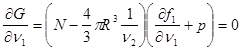 (4.42а) (4.42а)
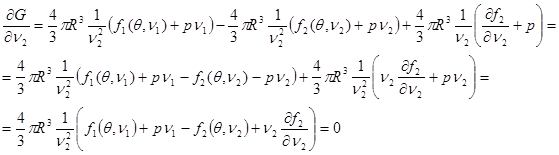 (4.42б) (4.42б)
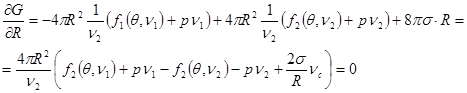 (4.42в) (4.42в)
Проанализируем полученное равенство. Из (4.42а) следует:
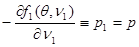 (4.43) (4.43)
Его смысл в том, что давление 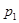 в фазе 1 равно внешнему давлению. в фазе 1 равно внешнему давлению.
Вводя выражения для химических потенциалов каждой из фаз и учитывая
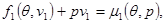

запишем (4.42б) в виде:
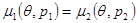 (4.44) (4.44)
Здесь  - давление во II фазе. Отличие уравнения (4.44) от условия равновесия фаз (4.25) в том, что давление в (4.44) в каждой из фаз может быть различным. - давление во II фазе. Отличие уравнения (4.44) от условия равновесия фаз (4.25) в том, что давление в (4.44) в каждой из фаз может быть различным.
Из равенства (4.42в) следует:
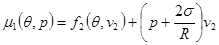 . .
Сравнивая полученное равенство с (4.44) и выражением для химического потенциала, получим формулу для давления газа внутри сферического пузырька:
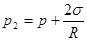 (4.45) (4.45)
Уравнение (4.45) представляет собой известную из курса общей физики формулу Лапласа. Обобщая (4.44) и (4.45) запишем условия равновесия между жидкостью и пузырьком пара в виде:
 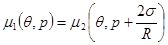 (4.46) (4.46)
В случае исследования задачи фазового перехода жидкость – твердое тело ситуация существенно осложняется в связи с необходимостью учета геометрических особенностей кристаллов, анизотропии направления преимущественного роста кристалла.
5.
Фазовые переходы наблюдаются и в более сложных случаях, при которых разрыв терпят только вторые производные химического потенциала по температуре и давлению. В этом случае кривая фазового равновесия определяется не одним, а тремя условиями:
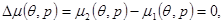 (4.47а) (4.47а)
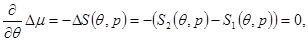 (4.47б) (4.47б)
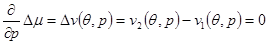 (4.47в) (4.47в)
Фазовые переходы, удовлетворяющие уравнениям (4.47), получили название фазовых переходов II рода. Очевидно, скрытая теплота фазового перехода и изменение удельного объема в этом случае равно нулю:
 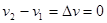 (4.48) (4.48)
Для получения дифференциального уравнения кривой фазового равновесия использовать уравнение Клапейрона – Клаузиуса (4.35) нельзя, т.к. при непосредственной подстановке в выражение (4.35) значений (4.48), получается неопределенность 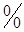 . Учтем, что при движении вдоль кривой . Учтем, что при движении вдоль кривой 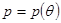 фазового равновесия сохраняется условие фазового равновесия сохраняется условие 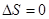 и и 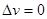 . Тогда: . Тогда:
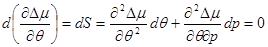
(4.49)
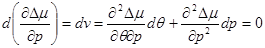 
Вычислим производные в (4.49)
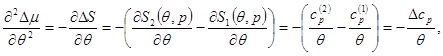 (4.50а) (4.50а)
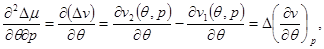 (4.50б) (4.50б)
 (4.50в) (4.50в)
Подставляя полученные выражения в (4.49), находим:
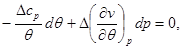 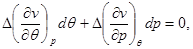 (4.51) (4.51)
Система линейных уравнений (4.51), записанная относительно 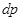 и и 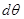 является однородной. Поэтому ее нетривиальное решение существует только в том случае, если определитель, составленный из коэффициентов равен нулю. Поэтому запишем является однородной. Поэтому ее нетривиальное решение существует только в том случае, если определитель, составленный из коэффициентов равен нулю. Поэтому запишем
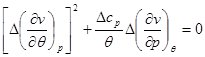 или или 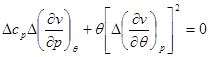
Учитывая полученное условие и выбирая из системы (4.51) любое уравнение, получаем:
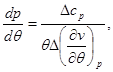 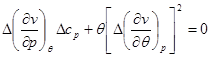 (4.52) (4.52)
Уравнения (4.52) для кривой фазового равновесия в случае фазового перехода II рода получили название уравнений Эренфеста. В этом случае кривая фазового равновесия может быть определено по известным характеристикам скачков теплоемкости  , коэффициента теплового расширения , коэффициента теплового расширения 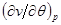 , коэффициента упругости , коэффициента упругости 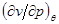 . .
Фазовые переходы второго рода встречаются значительно ранее фазовых переходов I рода. Это очевидно даже из условия (4.47), которое значительно жестче уравнения кривой фазового равновесия (4.юю) с условиями (4.31). Примерами таких фазовых переходов может служить переход проводника из сверхпроводящего состояния в нормальное при отсутствии магнитного поля.
Кроме того, встречаются фазовые переходы с равной нулю скрытой теплотой 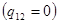 , для которых при переходе наблюдается наличие сингулярности в калорическом уравнении (теплоемкость терпит разрыв второго рода). Такой тип фазовых переходов носит название фазового перехода , для которых при переходе наблюдается наличие сингулярности в калорическом уравнении (теплоемкость терпит разрыв второго рода). Такой тип фазовых переходов носит название фазового перехода 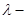 типа. Примерами таких переходов являются переход жидкого гелия из сверхтекучего состояния в нормальное, переход в точке Кюри для ферромагнетиков, переходы из неупругого состояния в упругое для сплавов типа. Примерами таких переходов являются переход жидкого гелия из сверхтекучего состояния в нормальное, переход в точке Кюри для ферромагнетиков, переходы из неупругого состояния в упругое для сплавов 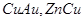 и т.д. и т.д.
|