Содержание
Введение
1 Алгоритм решения функциональной задачи
2 Выбор системы команд специализированной ЭВМ
3 Форматы команд и операндов
4 Содержательные графы микропрограмм операций АЛУ
5 Разработка объединенной микропрограммы работы АЛУ
6 Закодированные алгоритмы микропрограмм
7 Проектирование управляющего автомата
Целью курсового проектирования является закрепление знаний по курсу: «Организация ЭВМ и систем» , полученных в результате изучения лекционного курса и выполнения лабораторного практикума.
Объектом курсового проектирования является процессор специализированной ЭВМ.
В процессоре выделяют устройство, в котором выполняются все основные (арифметические и логические) операции. Это устройство называют арифметико-логическим устройством (АЛУ). Если все основные операции выполняются за один такт (это имеет место в большинстве современных микропроцессоров), АЛУ является частью операционного автомата процессора; если же некоторые или все основные операции выполняются алгоритмически за много тактов, АЛУ имеет собственное устройство управления.
Разработка процессора специализированной ЭВМ включает в себя следующие этапы:
- Разработка алгоритма решения функциональной задачи.
- Выбор системы команд специализированной ЭВМ.
- Определение форматов команд и операндов.
- Разработка алгоритмов микропрограмм выполнения минимально необходимого набора операций АЛУ.
- Разработка объединенной микропрограммы работы АЛУ.
- Разработка структурной схемы операционного автомата АЛУ.
- Разработка управляющего автомата АЛУ.
Укрупненный алгоритм решения поставленной задачи представлен на рисунке 1.1. Алгоритм вычисления функций F приведен соответственно на рисунке 1.2.

Рис.1.1 Укрупненный алгоритм
Для вычисления функции F можно воспользоваться степенным рядом:
Функция Arth(x) разлагается [3] в степенной ряд: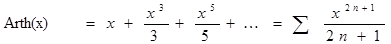
Этот ряд сходится при |x|<1, 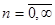
        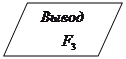
 . Сумму ряда удобно находить с помощью рекуррентных соотношений. Общий член ряда
. Сумму ряда удобно находить с помощью рекуррентных соотношений. Общий член ряда  выражается в данном случае через предыдущий член ряда с помощью равенства: выражается в данном случае через предыдущий член ряда с помощью равенства:
Для двухадресной системы команд без признака засылки основные операции над двумя операндами будут выглядеть так:
 , ,
где
А1
– первый адрес в команде;
А2
– второй адрес в команде;
* - обозначение операции.
Введем обозначение:
N . Наименование операции . X . Y
X – первый операнд и результат операции.
Y – второй операнд (если он не участвует, то ставится -).
Для двухадресной системы команд без признака засылки программа будет выглядеть так:
Часть команд в этой программе имеют два адреса, а часть – один адрес, поэтому и система команд ЭВМ должна состоять из одноадресных и двухадресных команд.
3 Форматы команд и операндов
Будем считать, что оперативная память (ОП) состоит из 256 ячеек длиной в один байт каждая.
Двухадресная система команд без признака засылки содержит 13 различных наименований команд, для кодирования которых поле КО должно иметь 4 разряда.
Поскольку в данном случае имеются одноадресные команды и двухадресные команды, для их различия введено одноразрядное поле кода длины команды (КДК) и принято считать: КДК=1 - для одноадресных и КДК=0 - для двухадресных команд.
Разряды 5-7 первого байта всех команд здесь не используются. Формат команд приведен на рисунке 3.1.
В качестве операнда будет использоваться 16-разрядное слово, запятая считается фиксированной перед старшим разрядом, а ОП оперирует с однобайтовыми словами. Формат операнда в ОП представлен на рисунке 3.2:
Такой операнд загружается за два обращения к ОП, здесь старшие разряды операнды и знак содержатся в первом байте, а младшие разряды – во втором.
Числа представляются в 16-разрядном формате, старший (нулевой) разряд используется для представления знака числа, для операции сложения используется модифицированный дополнительный код, поэтому регистр RG имеет 17 разрядов (0:16) (поле RG(1:16) – для хранения первого слагаемого), регистр RG1 имеет 16 разрядов RG1(0:15) – для второго слагаемого, одноразрядному полю признака переполнения изначально присвоено нулевое значение, при операции сложения слагаемые помещаются по младшим разрядам, результат (сумма) помещается в поле RG(1:16), прибавление константы 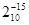 означает прибавление 1 к младшему разряду слова. означает прибавление 1 к младшему разряду слова.
Содержательный алгоритм сложения представлен на рисунке 4.1:

Рисунок 4.1 – Алгоритм операции сложения
Описание слов, использованных в микропрограмме сложения, представлены в таблице 4.1:
Таблица 4.1
| Тип |
Слово |
Пояснение |
| ILO |
RG(0:16) |
Слагаемое (Сумма) |
| IL |
RG1(0:16) |
Слагаемое |
| ILO |
ПП |
Признак переполнения |
Содержательный алгоритм вычитания представлен на рисунке 4.2:

Рисунок 4.2 – Алгоритм вычитания
Описание слов, использованных в микропрограмме вычитания представлены в таблице 4.2:
Таблица 4.2
| Тип |
Слово |
Пояснение |
| ILO |
RG(0:16) |
Уменьшаемое (разность) |
| IL |
RG1(0:16) |
Вычитаемое |
| ILO |
ПП |
Признак переполнения |
Содержательный алгоритмы умножения и деления представлены на рисунках 4.3 и 4.4:
Описания слов, использованных в микропрограммах представлены в таблицах 4.3 и 4.4:
Таблица 4.3
| Тип |
Слово |
Пояснение |
| ILO |
RG(0:16) |
Множитель, произведение |
| IL |
RG1(0:16) |
Множимое |
| L |
RG2(0:16) |
Множитель, произведение |
| L |
СТ(1:4) |
Счетчик циклов |
Таблица 4.4
| Тип |
Слово |
Пояснение |
| ILO |
RG(0:16) |
Делимое, остаток, частное |
| IL |
RG1(0:16) |
Делитель |
| L |
RG2(0:16) |
Частное |
| L |
СТ(1:4) |
Счетчик |
| ILO |
ПП |
Признак переполнения |
Содержательные алгоритмы умножения на 2 и нахождения абсолютной величины числа представлены на рисунке 4.5 и 4.6, а описания слов, использованных в микропрограммах – в таблице 4.5 и 4.6:
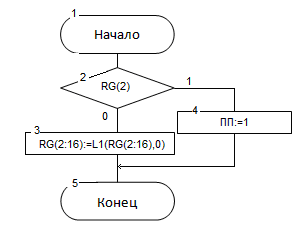
Рисунок 4.5 – Алгоритм операции «умножение на 2»

Рисунок 4.6 – Алгоритм приведения абсолютной величины числа
Таблица 4.5
| Тип |
Слово |
Пояснение |
| ILO |
RG(2:16) |
Операнд |
| ILO |
ПП |
Признак переполнения |
Таблица 4.6
| Тип |
Слово |
Пояснение |
| ILO |
RG(0:1) |
Операнд |
Содержательный алгоритм микропрограммы специальной функции Arth(x) представлен на рисунке 4.7, здесь до начала выполнения программы регистру RG4 присваивается значение X. Описания слов, использованных в микропрограмме – в таблице 4.7:
Таблица 4.7
| Тип |
Слово |
Пояснение |
| ILO |
RG(0:16) |
Переменная x,n,b,a,F множитель, произведение, делимое,
остаток, частное, слагаемое, сумма,
уменьшаемое, разность
|
| IL |
RG1(0:15) |
Переменная F,b,a
константа,
Множимое, делитель, слагаемое, вычитаемое
|
| L |
RG2(0:16) |
Множитель, произведение, частное |
| L |
RG3(0:15) |
Переменная F |
| L |
RG4(0:15) |
Переменная x,a,b |
| L |
RG5(0:15) |
Переменная n |
| L |
CT(1:4) |
Счетчик |
| ILO |
ПП |
Признак переполнения |
Теперь необходимо составить схему укрупненного алгоритма, используя уже полученную микропрограмму вычисления функции Arth(x). Предполагается, что переменные x1, x2 и x3 перед началом выполнения программы уже будут загружены соответственно в регистры RG4, RG3 и RG5. Данная схема алгоритма представлена на рисунке 4.8:

Рисунок 4.8 – Схема алгоритма
В таблице 4.8 представлено описание слов, использованных в программе. Так как описание слов для микропрограммы вычисления специальной функции было представлено в таблице 4.7, здесь приводится описание только тех слов, которые принимали значения отличные от тех, что использовались в алгоритме на рисунке 4.7.
Таблица 4.8
| Тип |
Слово |
Пояснение |
| ILO |
RG(0:16) |
Переменная x1, x2,X делимое,
остаток, частное,
уменьшаемое, разность
абсолютная величина числа
|
| IL |
RG1(0:15) |
Переменная x2, x3
константа, делитель, вычитаемое
|
| L |
RG3(0:15) |
Переменная x2 |
| L |
RG4(0:15) |
Переменная x1, X |
| L |
RG5(0:15) |
Переменная x3 |
5 Разработка объединенной микропрограммы работы АЛУ
Процессор состоит из АЛУ и УЦУ.
В объединенном списке микроопераций, используемых в микропрограммах минимального набора операций АЛУ, для унификации формы записи различных операций и форматов одноименных слов следует по сравнению с рисунком 4.3 изменить три микрооперации:
- для вершины 2 вместо микрооперации RG2 := RG нужно использовать микрооперацию RG2 := RG(1:16).0;
- для вершины 6 вместо микрооперации RG2(1:15):=R1(RG (15).RG2(1:15)) – использовать микрооперацию RG2(1:15):=R1(RG(16).RG2(1:16);
- вместо микрооперации RG(0):=1 в вершине 11 – использовать микрооперацию RG(0:1):=11.
Благодаря этим изменениям значение числовой части результата каждой операции присваивается полю RG(2:16) слова RG, а нулевой и первый разряды этого слова используются для представления знака числа. Появляется возможность считать, что перед началом каждой операции над двумя операндами в АЛУ значение первого операнда присваивается полю RG(1:16) слова RG, а значение второго операнда – слову RG1. При выполнении этого условия перед началом сложения и вычитания необходимо произвести присваивание RG(0) := RG(1), перед началом умножения нужно осуществить передачу RG2 := RG(1:16).0, а перед делением – микрооперации RG2(0):= RG(1) и RG(0:1):= 00.
В таблице 5.1 приведен список логических условий, используемых в микропрограммах:
Таблица 5.1
| Обозначение |
Лог. Условие |
Тип операции |
| X1 |
RG(0) |
Сложение и
Вычитание
|
| X2 |
RG1(0) |
| X3 |
RG(1) |
| X4 |
RG2(15) |
Умножение |
| X5 |
CT=0 |
| X6 |
RG2(1) |
| X7 |
RG1(0)ÅRG2(0) |
Деление |
| X8 |
RG2(16) |
Умножение на «2» |
| X9 |
RG(2) |
Вычисление функции Arth(x) |
| X10 |
RG(0:16) |
В таблице 5.2 приведен список микроопераций, используемых в микропрограммах:
Таблица 5.2
| № |
Микрооперации |
Тип операции |
| Y1 |
RG(0):=RG(1) |
Сложение |
| Y2 |
RG(2:16):=ù RG(2:16) + 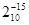 |
| Y3 |
RG:=RG+RG1(1:15) |
| Y4 |
RG:=RG+11.ù RG1(1:15)+ 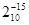 |
| Y5 |
ПП:=1 |
| Y6 |
RG1(0):= ù RG1(0) |
Вычитание |
| Y7 |
RG2:=RG(1:16).0 |
Умножение |
| Y8 |
RG:=0 |
| Y9 |
CT:=1510 |
| Y10 |
RG2(1:16):=R1(RG(16).RG2(1:16)) |
| Y11 |
RG(1:16):=R1(0.RG(1:16)) |
| Y12 |
CT:=CT-1 |
| Y13 |
RG:=RG+ 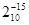 |
| Y14 |
RG(0:1):=11 |
| Y15 |
RG2(0):=RG(1) |
Деление |
| Y16 |
RG(2:16):=L1( RG(2:16).0) |
| Y17 |
CT:=0 |
| Y18 |
RG2(1:16):=0 |
| Y19 |
RG2(1:16):=L1(RG2(1:16).ù RG(0)) |
| Y20 |
RG:=RG2(1:15) |
| Y21 |
RG(0:1):=00 |
Выделение абсолютной величины числа |
| Y22 |
RG3:=RG4 |
Вычисление функции Arth(x) |
| Y23 |
RG5:= 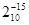 |
| Y24 |
RG:=RG4 |
| Y25 |
RG1:=RG |
| Y26 |
RG4:=RG |
| Y27 |
RG:=RG5 |
| Y28 |
RG4:=RG1 |
| Y29 |
RG1:= 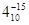 |
| Y30 |
RG5:=RG5+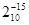 |
| Y31 |
RG:=RG3 |
В приложениях 1, 2 и 3 приведена соответственно схема объединенной микропрограммы работы АЛУ, закодированная схема объединенной микропрограммы работы АЛУ и структурная схема операционного автомата.
Закодированные алгоритмы сложения, вычитания, умножения, деления, умножения на «2» и выделения абсолютной величины числа представлены соответственно на рисунках 6.1, 6.2, 6.3, 6.4, 6.5 и 6.6:
7 Проектирование управляющего автомата
Формат микрокоманды при вертикальном кодировании имеет формат, представленный на рисунке 7.1:
Формат команды с принудительной адресацией представлен на рисунке 7.2:
Алгорим формирования исполнительного адреса обращения к микропрограммной памяти (МПП) представлен на рисунке 7.3:

Рисунок 7.3 – Алгоритм формирования адреса
В таблице 7.1 приведены все микрооперации, расположенные в микропрограммной памяти, где адрес A0 - переход по «истина»:
Таблица 7.1
| Логичеcкий адрес МК в МПП |
Формат микрокоманды |
| Операционная зона |
Адресная зона |
| Y |
X(1..l) |
A0 |
A1 |
| 0 |
Y0 |
1 |
| 1 |
Y31 |
2 |
| 2 |
Y33 |
3 |
| 3 |
Y15 |
4 |
| 4 |
Y21 |
5 |
| 5 |
Y4 |
6 |
| 6 |
X1 |
23 |
7 |
| 7 |
Y16 |
| 8 |
Y9 |
9 |
| 9 |
Y18 |
10 |
| 10 |
X1 |
12 |
11 |
| 11 |
Y4 |
13 |
| 12 |
Y3 |
13 |
| 13 |
Y19 |
14 |
| 14 |
Y16 |
15 |
| 15 |
Y12 |
16 |
| 16 |
X5 |
17 |
10 |
| 17 |
Y20 |
18 |
| 18 |
X8 |
19 |
20 |
| 19 |
Y13 |
| 20 |
X7 |
22 |
21 |
| 21 |
Y21 |
24 |
| 22 |
Y14 |
24 |
| 23 |
Y5 |
24 |
| 24 |
Y25 |
25 |
| 25 |
Y24 |
26 |
| 26 |
Y6 |
27 |
| 27 |
Y1 |
28 |
| 28 |
X1 |
29 |
30 |
| 29 |
Y2 |
30 |
| 30 |
X2 |
32 |
31 |
| 31 |
Y3 |
33 |
| 32 |
Y4 |
33 |
| 33 |
X1 |
35 |
34 |
| 34 |
X2 |
36 |
38 |
| 35 |
X2 |
37 |
36 |
| 36 |
Y5 |
38 |
| 37 |
Y2 |
38 |
| 38 |
Y26 |
39 |
| 39 |
Y21 |
40 |
| 40 |
Y34 |
41 |
| 41 |
Y6 |
42 |
| 42 |
Y1 |
43 |
| 43 |
X1 |
44 |
45 |
| 44 |
Y2 |
45 |
| 45 |
X2 |
47 |
46 |
| 46 |
Y3 |
48 |
| 47 |
Y4 |
48 |
| 48 |
X1 |
50 |
49 |
| 49 |
X2 |
51 |
53 |
| 50 |
X2 |
52 |
51 |
| 51 |
Y5 |
53 |
| 52 |
Y2 |
53 |
| 53 |
X1 |
0 |
54 |
| 54 |
Y22 |
55 |
| 55 |
Y23 |
56 |
| 56 |
Y24 |
57 |
| 57 |
Y25 |
58 |
| 58 |
Y7 |
59 |
| 59 |
Y8 |
60 |
| 60 |
Y9 |
61 |
| 61 |
X4 |
62 |
63 |
| 62 |
Y3 |
63 |
| 63 |
Y10 |
64 |
| 64 |
Y11 |
65 |
| 65 |
Y12 |
66 |
| 66 |
X5 |
67 |
61 |
| 67 |
X6 |
68 |
69 |
| 68 |
Y13 |
69 |
| 69 |
X7 |
70 |
71 |
| 70 |
Y14 |
71 |
| 71 |
Y26 |
72 |
| 72 |
Y27 |
73 |
| 73 |
X9 |
75 |
74 |
| 74 |
Y16 |
76 |
| 75 |
Y5 |
76 |
| 76 |
Y6 |
77 |
| 77 |
Y1 |
78 |
| 78 |
X1 |
79 |
80 |
| 79 |
Y2 |
80 |
| 80 |
X2 |
82 |
81 |
| 81 |
Y3 |
83 |
| 82 |
Y4 |
83 |
| 83 |
X1 |
85 |
84 |
| 84 |
X2 |
86 |
88 |
| 85 |
X2 |
87 |
86 |
| 86 |
Y5 |
88 |
| 87 |
Y2 |
88 |
| 88 |
Y25 |
89 |
| 89 |
Y24 |
90 |
| 90 |
Y28 |
91 |
| 91 |
Y7 |
92 |
| 92 |
Y8 |
93 |
| 93 |
Y9 |
94 |
| 94 |
X4 |
95 |
96 |
| 95 |
Y3 |
96 |
| 96 |
Y10 |
97 |
| 97 |
Y11 |
98 |
| 98 |
Y12 |
99 |
| 99 |
X5 |
100 |
94 |
| 100 |
X6 |
101 |
102 |
| 101 |
Y13 |
102 |
| 102 |
X7 |
103 |
104 |
| 103 |
Y14 |
104 |
| 104 |
Y25 |
105 |
| 105 |
Y24 |
106 |
| 106 |
Y28 |
107 |
| 107 |
Y29 |
108 |
| 108 |
Y1 |
109 |
| 109 |
X1 |
110 |
111 |
| 110 |
Y2 |
111 |
| 111 |
X2 |
113 |
112 |
| 112 |
Y3 |
114 |
| 113 |
Y4 |
114 |
| 114 |
X1 |
116 |
115 |
| 115 |
X2 |
117 |
38 |
| 116 |
X2 |
118 |
117 |
| 117 |
Y5 |
119 |
| 118 |
Y2 |
119 |
| 119 |
Y25 |
120 |
| 120 |
Y24 |
121 |
| 121 |
X10 |
122 |
158 |
| 122 |
Y15 |
123 |
| 123 |
Y21 |
124 |
| 124 |
Y4 |
125 |
| 125 |
X1 |
142 |
126 |
| 126 |
Y16 |
127 |
| 127 |
Y9 |
128 |
| 128 |
Y18 |
129 |
| 129 |
X1 |
131 |
130 |
| 130 |
Y4 |
132 |
| 131 |
Y3 |
132 |
| 132 |
Y19 |
133 |
| 133 |
Y16 |
134 |
| 134 |
Y12 |
135 |
| 135 |
X5 |
136 |
129 |
| 136 |
Y20 |
137 |
| 137 |
X8 |
138 |
139 |
| 138 |
Y13 |
139 |
| 139 |
X7 |
141 |
140 |
| 140 |
Y21 |
143 |
| 141 |
Y14 |
143 |
| 142 |
Y5 |
143 |
| 143 |
Y30 |
144 |
| 144 |
Y31 |
145 |
| 145 |
Y32 |
146 |
| 146 |
Y1 |
147 |
| 147 |
X1 |
148 |
149 |
| 148 |
Y2 |
149 |
| 149 |
X2 |
150 |
151 |
| 150 |
Y3 |
152 |
| 151 |
Y4 |
152 |
| 152 |
X1 |
154 |
153 |
| 153 |
X2 |
155 |
157 |
| 154 |
X2 |
156 |
155 |
| 155 |
Y5 |
157 |
| 156 |
Y2 |
157 |
| 157 |
71 |
| 158 |
Y0 |
|