Зміст
ІІ Молекулярна фізика і термодинаміка
5 Загальні положення та поняття теорії
1 Предмет дослідження. Термодинамічні системи. Термодинамічні параметри. Термодинамічний та статистичний методи дослідження термодинамічних систем.
2 Ідеальний газ як модельне тіло для дослідження термодинамічних систем. Дослідні газові закони. Рівняння стану ідеальних газів.
3 Основні положення та основні поняття молекулярно-кінетичної теорії. Фізичний зміст термодинамічних параметрів. Теорема про рівнорозподіл енергії за ступенями свободи (принцип Больцмана) Внутрішня енергія ідеального газу.
6 Елементи статистичної фізики
1 Статистичний метод дослідження термодинамічних систем. Зв’язок термодинамічних параметрів з динамічними характеристиками руху молекул. Відомості з теорії ймовірностей. Статистичний розподіл молекул та його значення.
2 Максвелівський розподіл молекул за швидкостями. Середньостатистичні значення швидкостей руху молекул та їх взаємозв’язок.
3 Барометрична формула. Досліди Перена з визначення числа Авогадро. Класичний розподіл молекул за енергіями
7 Термодинаміка. Перший закон термодинаміки
1 Термодинамічна система. Внутрішня енергія термодинамічної системи. Робота та кількість теплоти. Перший закон термодинаміки
2 Теплоємність тіл. Застосування першого закону термодинаміки до ізопроцесів. Теплоємність ідеальних газів в ізопроцесах
3 Адіабатичний процес. Внутрішня енергія та робота в адіабатичному процесі. Рівняння Пуасона.
8 Другий закон термодинаміки
1 Термодинамічні процеси. Оборотні та необоротні процеси. Колові процеси (цикли). Коефіцієнт корисної дії (ККД) циклу
2 Цикл Карно та його ККД. Зведена теплота. Ентропія. Вільна та зв’язана частини внутрішньої енергії.
3 Теорема Карно. Другий закон термодинаміки. Абсолютна термодинамічна шкала температур
4 Статистичне тлумачення ентропії та другого закону термодинаміки. Нерівність Клаузиуса та критика теплової смерті всесвіту
5
Загальні положення та поняття теорії
1
Предмет дослідження. Термодинамічні системи. Термодинамічні параметри. Термодинамічний та статистичний методи дослідження термодинамічних систем.
2
Ідеальний газ як модельне тіло для дослідження термодинамічних систем. Дослідні газові закони. Рівняння стану ідеальних газів.
3
Основні положення та основні поняття молекулярно-кінетичної теорії. Фізичний зміст термодинамічних параметрів. Теорема про рівнорозподіл енергії за ступенями свободи (принцип Больцмана) Внутрішня енергія ідеального газу.
1 Предмет дослідження. Термодинамічні системи. Термодинамічні параметри. Термодинамічний та статистичний методи дослідження термодинамічних систем.
Будову та внутрішній рух тіл та систем, що складаються з дуже великої кількості складових елементів (атомів, молекул, елементарних часток, інших тіл, навіть зірок та інших небесних тіл - молекул в подальшому) вивчають два взаємодоповнюючих розділи фізики: молекулярна фізика та термодинаміка. Предмет їх дослідження носить назву термодинамічної системи. Дослідження термодинамічних систем відбувається принципово різними методами, які взаємно доповнюють один одного.
Термодинамічними
називаються системи
, що містять значну кількість складових елементів (теоретично N @ 1010
...1020
елементів) і підкоряються законам термодинаміки. На практиці буває досить кількох сотень складових елементів. Величини, що характеризують стан термодинамічної системи, носять назву параметрів стану. Основним параметром стану термодинамічної системи є її температура (Т
). Температура
характеризує ступінь нагрітості системи і визначається через поняття теплової рівноваги системи чи систем. Тілам, що знаходяться в стані теплової рівноваги приписується однакова температура. Вимірюється температура термометрами
.
Зміна температури системи призводить до зміну об’єму тіл, або тиску, або внутрішньої електропровідності і таке інше. Ці зміни легко відмічаються і використовуються для вимірів температури. Властивості
, зміна яких використовується для вимірів температури, називаються термометричними
, а тіла, що мають такі властивості, називаються термометричними тілами
. Термометричні тіла становлять основу будови термометрів
- приладів для вимірювання температури.
В міжнародній системі одиниць SІ температура вимірюється в кельвінах (К). Один кельвін
- це одна сота температурного інтервалу від потрійної точки рівноваги води (рідина, лід і пара) до точки її кипіння. В наукових дослідженнях використовується абсолютна термодинамічна шкала температур, яка будується за розглядом особливостей коефіцієнта корисної дії (ККД) теплових машин. Тому, що він не може бути рівним нулю, або бути більшим за нуль, термодинамічна температура може бути тільки позитивною (або тільки від’ємною, за домовленістю), абсолютний нуль температури - теоретично недосяжна величина. В протилежному випадку ККД теплових машин міг бути 100%
або більше, що суперечить другому закону термодинаміки (і людському досвіду).
В практиці використовуються різні шкали. Найбільше використання має шкала Цельсія, де за нуль приймається точка танення льоду (потрійна точка), а за 100о
С
- точка кипіння води. Одиниця вимірювання - 1о
С = 1К
.
Значення температури за різними шкалами зв’язані між собою: t = =Т
‑273 К
, де t
- температура за шкалою Цельсія; Т
- температура за абсолютною термодинамічною шкалою.
Молекулярно-кінетична теорія надає температурі фізичного змісту, як величині пропорційній середній кінетичній енергії поступального руху молекул.
Внутрішньою енергією (Е
) називається енергія тіл, що складають систему. В найпростішому випадку вважається, що в системі не відбувається ні хімічних, ні термоядерних, ні інших перетворень такого роду. Тому внутрішня енергія системи - це енергія механічного руху (кінетична і потенціальна) структурних елементів (молекул), що створюють систему, енергія їх неупорядкованого руху.
Кількість теплоти (Q
) є міра зміни внутрішньої енергії в теплових процесах, що не супроводжуються виконання механічної роботи (тобто в процесах, де внутрішня енергія хаотичного руху одних тіл переходить у внутрішню енергію інших тіл системи чи систем). Кількість теплоти, як і внутрішня енергія, вимірюється в джоулях.
Якщо параметри термодинамічної системи фіксовані, то йдеться про стан системи
. Стан
називається рівноважним
, якщо кожен з параметрів у всіх точках системи має однакове значення.
Зміна стану термодинамічної системи називається термодинамічним процесом
. Термодинамічний процес, що відбувається через проміжні рівноважні стани, називається квазістатичним
.
2
Ідеальний газ як модельне тіло для дослідження термодинамічних систем. Дослідні газові закони. Рівняння стану ідеальних газів.
Для вивчення найбільш загальних властивостей термодинамічних систем вводиться модельна термодинамічна система – ідеальний газ. Ідеальний газ, в цьому сенсі, це термодинамічна система, що має найбільш загальні властивості всіх термодинамічних систем.
Ідеальний газ є досить корисним для вивчення найбільш загальних властивостей речовини. При вивченні різних властивостей ця модель корегується відповідним чином. Найбільш проста модель ідеального газу використовується при вивченні загальних властивостей газів. Ця модель повинна мати найбільш характерні властивості присутні газовому стану речовини.
Молекулярно-кінетична теорія свідчить, що при переході речовини в газоподібний стан значно збільшується середня відстань між молекулами і стає значною порівняно з розмірами молекул; руйнуються дальній і ближній порядки в розташуванні молекул і їх рух стає хаотичним; сили взаємодії між молекулами на відстанях, що дорівнюють середнім, стають досить малими. Тому ідеальний газ
для вивчення поведінки газів - це газ, що складається з матеріальних точок, які рухаються абсолютно хаотично і сили взаємодії між якими відсутні.
Для ідеальних газів справедливий закон Авогадро, який стверджує, що в рівних об’ємах при рівних умовах міститься однакове число молекул. Один моль довільної речовини містить NА
= 6,023
×
1023
моль-1
- число Авогадро молекул. На підставі закону Авогадро моль ідеальних газів при нормальних умовах (тиск Ро
= 760 мм рт.ст. = 1,015
×
105
Па;
температура То
= 273,15 К
) займає один і той же, незалежно від природи ідеального газу, об’єм, що, як показує досвід, дорівнює Vм
= 22,4
×
10-3
м3
/моль
.
Для суміші ідеальних газів справедливий закон Дальтона: тиск суміші газів дорівнює сумі парціальних тисків газів суміші:
Р = Р1
+ Р2
+ ... + Рn
.
(5.1)
Парціальним тиском Рі
називається тиск, що його чинив би і
-тий ідеальний газ суміші, якби він займав самостійно об’єм посудини. Цей закон є відображенням принципу суперпозиції, принципу незалежності дії сил.
Співвідношення між параметрами одного і того ж стану термодинамічної системи носить назву рівняння стану; співвідношення, що встановлює зв’язок між параметрами термодинамічної системи в різних станах термодинамічного процесу, носить назву закону.
Закони ідеальних газів були встановлені дослідним шляхом і мають місце для постійної маси ідеального газу. Термодинамічні процеси, що відбуваються за постійного значення одного з параметрів, називаються ізопроцесами
.
Ізотермічний процес
було досліджено дослідниками Бойлем та Маріоттом. Закон Бойля-Маріотта стверджує, що для постійної маси ідеального газу за сталої температури добуток тиску на об’єм залишається незмінним:
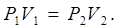 (5.2) (5.2)
Графік цього процесу (рис. 4.1), представлений на діаграмах „P‑V”, „P‑T” або „V‑T”, - називається ізотермою.
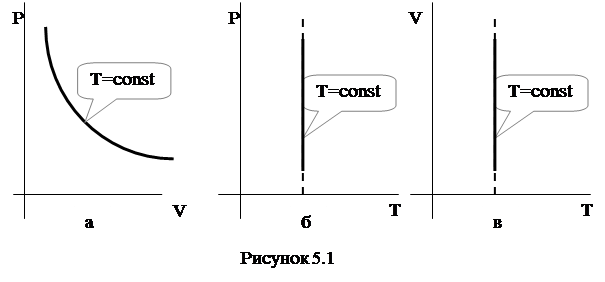
Найбільш вживаним є графік у формі рис. 5.1 а.
Ізобарний(ізобарний) процес
підкоряється закону Гей Люссака
: для постійної маси ідеального газу за постійного тиску об’єм зростає прямо пропорційно до зростання температури:
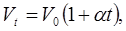 (5.3) (5.3)
де
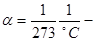
температурний коефіцієнт, сталий для всіх ідеальних газів; V
0
– об’єм газу за нуля градусів температури за Цельсієм. Якщо ввести абсолютну температуру Т= t+273 K, то закон Гей Люссака перепишеться в компактній формі:
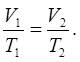 (5.4) (5.4)
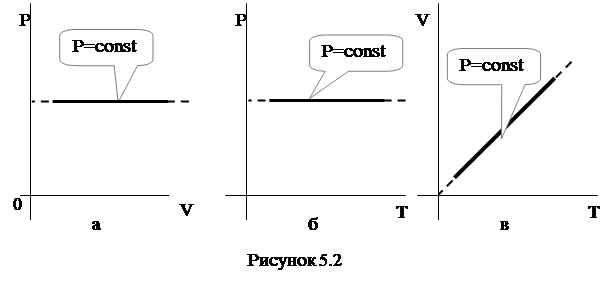
Графік цього процесу (рис. 5.2), представлений на діаграмах „P‑V”,
„P‑T” або „V‑T”, - називається ізобарою
.
Найбільш інформативним є графік рис. 5.2в, він свідчить про те, що об’єм ідеального газу за температури, що прагне до абсолютного нуля, також прагне до нуля – за припущенням ідеальний газ складається з матеріальних точок. Реальні гази не можуть мати нульового об’єму, за досить низьких температур газ перестане відповідати умовам ідеального газу.
Ізохоричний (ізохорний) процес
підкоряється закону Шарля
: для постійної маси ідеального газу за постійного об’єму тиск зростає прямо пропорційно до зростання температури:
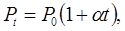 (5.4) (5.4)
де 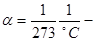 температурний коефіцієнт, сталий для всіх ідеальних газів; Р
0
– об’єм газу за нуля градусів температури за Цельсієм. Якщо ввести абсолютну температуру Т= t+273 K, то закон Шарля
перепишеться в компактній формі: температурний коефіцієнт, сталий для всіх ідеальних газів; Р
0
– об’єм газу за нуля градусів температури за Цельсієм. Якщо ввести абсолютну температуру Т= t+273 K, то закон Шарля
перепишеться в компактній формі:
 (5.5) (5.5)
Графік цього процесу (рис. 4.3), представлений на діаграмах „P‑V”, „P‑T” або „V‑T”, - називається ізобарою
.
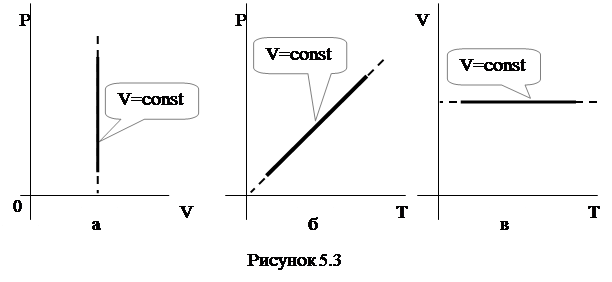
Найбільш інформативним є графік на рис.5.3 б, він свідчить про те, що тиск ідеального газу за температури, що прагне до абсолютного нуля, також прагне до нуля – за припущенням ідеальний газ складається з матеріальних точок, сили взаємодії між якими виключені. Зі зменшенням температури інтенсивність руху молекул зменшується, їх бомбардування стінок посудини зменшується, а за абсолютного нуля тиск стане нульовим. Реальні гази за досить низьких температур перестають відповідати умовам ідеального газу.
Скориставшись дослідними газовими законами, можна отримати об’єднаний газовий закон, що стверджує: для постійної маси ідеального газу добуток тиску на об’єм віднесений до абсолютної температури залишається незмінним в довільних процесах:
 (5.6) (5.6)
Виходячи з об’єднаного газового закону (5.6), можна отримати рівняння стану ідеальних газів. За нормальних умов (тиск Ро
= 1,015
×
105
Па;
температура То
= 273,15 К
) об’єм одного моля ідеального газу V0
=22,4∙10-3
м3
відповідно
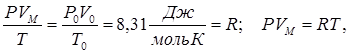 (5.7) (5.7)
де 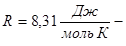 універсальна газова стала. універсальна газова стала.
Рівняння стану довільної маси ідеального газу зв’язує параметри його стану:
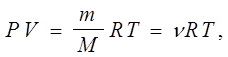 (5.8) (5.8)
де Р
- тиск; V -
об’єм; Т
- температура; m
- маса; М
- молярна маса газу; n
- кількість молів газу; R -
універсальна газова стала.
Одночасно вводиться стала Больцмана:
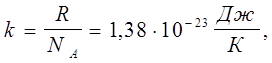 (5.9) (5.9)
яка широко використовується в молекулярній фізиці.
Рівняння стану (5.8) може бути переписане в інших формах призначених для визначення конкретних характеристик:
а) для густини речовини -
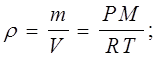 (5.10) (5.10)
б) для концентрації молекул -
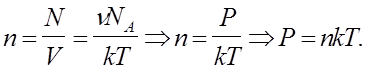 (5.11) (5.11)
3
Основні положення та основні поняття молекулярно-кінетичної теорії. Фізичний зміст термодинамічних параметрів. Теорема про рівнорозподіл енергії за ступенями свободи (принцип Больцмана) Внутрішня енергія ідеального газу.
Першою сформульованою теорією молекулярної фізики була молекулярно-кінетична теорія. В основі її лежать слідуючи положення: 1) всі речовини складаються з атомів та молекул; 2) атоми та молекули знаходяться в безперервному хаотичному тепловому рухові; 3) атоми та молекули взаємодіють між собою.
Атомом
називається найменша частинка хімічного елемента, що ще зберігає його основні фізичні (спектр електромагнітного випромінення) та хімічні (здатність вступати в хімічні реакції) властивості. Молекула
– це найменша частинка речовини, що ще зберігає його основні фізичні та хімічні властивості.
Виходячи з закону цілих кратних відношень мас хімічних елементів, що вступили в хімічну реакцію, було встановлено відносні маси всіх атомів. Якщо прийняти за одиницю маси (а.о.м.) 1/12 маси атому вуглецю 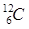 , то маси всіх атомів в а.о.м відомі і занесені в таблицю елементів. , то маси всіх атомів в а.о.м відомі і занесені в таблицю елементів.
Кількість речовини, що складається із стількох елементів, що і 12 г вуглецю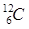 , носить назву моль речовини. Це число – число Авогадро , носить назву моль речовини. Це число – число Авогадро 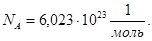 Маса моля речовини, виражена в грамах, чисельно дорівнює атомній масі елементу вираженій в а.о.м. Виходячи з маси моля, наприклад води - 18∙10-3
кг/моль, та з числа Авогадро, оцінимо масу молекули води, наприклад: Маса моля речовини, виражена в грамах, чисельно дорівнює атомній масі елементу вираженій в а.о.м. Виходячи з маси моля, наприклад води - 18∙10-3
кг/моль, та з числа Авогадро, оцінимо масу молекули води, наприклад: 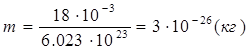 . Таким чином, маси атомів та молекул порядку 10-26
кг. Якщо густина води r= 103
кг/м3
, то об’єм одного моля води і об’єм що приходиться, в середньому, на одну молекулу, можна визначити: . Таким чином, маси атомів та молекул порядку 10-26
кг. Якщо густина води r= 103
кг/м3
, то об’єм одного моля води і об’єм що приходиться, в середньому, на одну молекулу, можна визначити: Звідки поперечні розміри атомів та молекул порядку 10-10 м. Концентрація атомів в конденсованій речовині, наприклад у воді, порядку 1029
м-3
. Звідки поперечні розміри атомів та молекул порядку 10-10 м. Концентрація атомів в конденсованій речовині, наприклад у воді, порядку 1029
м-3
.
Друге положення молекулярно-кінетичної теорії підтверджується броунівським рухом зважених у рідинах малесеньких частинок речовини процесами випаровування речовин і інше.
Особливості взаємодії атомів та молекул вивчались як на основі досліджень процесів стискування та розтягування тіл так і на основі сучасних теоретичних досліджень. Характер сил взаємодії між двома атомами (або молекулами) та потенціальної енергії цієї взаємодії представлений на графіках рис. 4.4. На осі відстаней між атомами вказана точка r0,
де сили взаємодії дорівнюють нулю, а потенціальна енергія взаємодії сягає свого мінімуму.
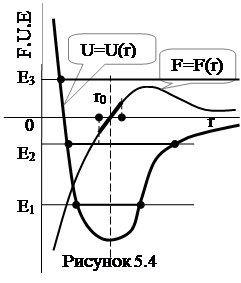
Агрегатний стан речовини залежить від температури, або середньої енергії Е
руху її молекул. Твердий стан речовин відповідає малій енергії руху молекул (Е1
на рис. 5.4). Молекули речовини можуть рухатись тільки в обмеженому інтервалі відстаней навколо деяких рівноважних положень, при цьому зберігається певна форма тіла в цілому.
Із збільшенням температури тіла (енергія руху молекул Е2
на рис. 5.4), енергії руху молекул вистачає, щоб, подолавши сили притягання, час від часу змінювати своє рівноважне положення і так званий ближній порядок, - такий рух молекул відповідає рідкому стану. І, коли енергія руху молекул досить велика (Е3
на рис. 5.4), рух молекул обмежується тільки стінками посудини, - маємо газоподібний стан речовини.
Основним рівнянням молекулярно-кінетичної теорії
називається рівняння, що зв’язує між собою характеристики руху молекул з макропараметри стану термодинамічної системи в цілому, вирішує тим саме основну задачу теорії, дає тлумачення фізичного змісту термодинамічних параметрів. Вивчення руху молекул ідеального газу дає можливість встановити такий зв’язок:
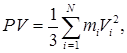 (5.12) (5.12)
де Р
– тиск; V
- об’єм газу; mi
таVi
– відповідно маса та швидкість руху і
- тої молекули; N
– загальна кількість молекул газу. Рівняння у вигляді (5.12) має символічну форму, тому що загальна кількість молекул дуже велика. Кажуть з цього приводу, що динамічні характеристики окремих молекул позбавлені фізичного змісту – з ними не можливо проводити розрахунки, фізичний зміст мають тільки середні значення цих характеристик, молекулярна фізика оперує тільки з ними.
Якщо розглядається газ з однорідних молекул масою mi
=
m
, то рівняння (5.12) приймає форму: 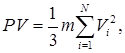 а а  де V
кв
– середньостатистична величина, що носить назву середня квадратична швидкість руху молекул
. Основне рівняння молекулярно-кінетичної теорії (5.12) приймає форму: де V
кв
– середньостатистична величина, що носить назву середня квадратична швидкість руху молекул
. Основне рівняння молекулярно-кінетичної теорії (5.12) приймає форму:
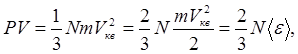 (5.13) (5.13)
де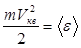 - середня кінетична енергія поступального руху молекул. - середня кінетична енергія поступального руху молекул.
Основне рівняння (5.13) дає можливість тлумачити фізичний зміст термодинамічних параметрів. Дійсно тиск
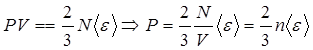 (5.14) (5.14)
визначається середньою енергією руху молекул та їх концентрацією.
Скориставшись рівнянням стану ідеального газу (5.11) отримаємо співвідношення для тлумачення температури: Абсолютна температура
є мірою середньої кінетичної енергії поступального руху молекул тіла (термодинамічної системи). Стала Больцмана
є коефіцієнтом пропорціональності між температурою і середньою кінетичною енергією поступального руху молекул Абсолютна температура
є мірою середньої кінетичної енергії поступального руху молекул тіла (термодинамічної системи). Стала Больцмана
є коефіцієнтом пропорціональності між температурою і середньою кінетичною енергією поступального руху молекул
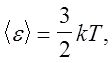 (5.15) (5.15)
вона встановлює співвідношення між джоулем і кельвіном.
Одним із фундаментальних положень класичної теорії є теорема про рівномірний розподіл енергії по ступенях свободи термодинамічної системи
.
Під ступенями свободи
розуміють кількість незалежних координат, необхідних для визначення положення тіла в просторі. Теорема стверджує, що на довільну ступінь свободи тіла в середньому приходиться одна і та сама енергія
[з цим положенням і узгоджується рівняння (5.6)]:
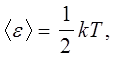 (5.16) (5.16)
де  - стала Больцмана. - стала Больцмана.
Ідеальним
є газ
, в якому відсутні сили взаємодії між молекулами. Тому внутрішня енергія ідеального газу
складається тільки з кінетичної енергії руху його молекул:
 (5.17) (5.17)
де N
- кількість молекул; і
- число ступенів свободи поступального, обертального і коливального внутрішнього рухів його молекул,
і = іпоступ
+ іоберт
+ 2іколив
. (5.18)
Внутрішні коливання атомів в молекулах ідеального газу включають кінетичну і потенціальну енергії, тому при врахуванні ступенів свободи молекул кількість коливальних ступенів свободи подвоюється.
Моль речовини має 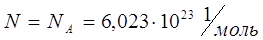 молекул, тому внутрішня енергія моля ідеального газу молекул, тому внутрішня енергія моля ідеального газу
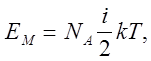 (5.19) (5.19)
Добуток 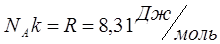 має назву універсальної газової сталої і вираз (5.19) приймає вигляд: має назву універсальної газової сталої і вираз (5.19) приймає вигляд:
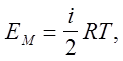 а енергія довільної маси газу а енергія довільної маси газу 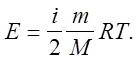 (5.20) (5.20)
6
Елементи статистичної фізики
1
Статистичний метод дослідження термодинамічних систем. Зв’язок термодинамічних параметрів з динамічними характеристиками руху молекул. Відомості з теорії ймовірностей. Статистичний розподіл молекул та його значення.
2
Максвелівський розподіл молекул за швидкостями. Середньостатистичні значення швидкостей руху молекул та їх взаємозв’язок.
3
Барометрична формула. Досліди Перена з визначення числа Авогадро. Класичний розподіл молекул за енергіями
1
Статистичний метод дослідження термодинамічних систем. Зв’язок термодинамічних параметрів з динамічними характеристиками руху молекул. Відомості з теорії ймовірностей. Статистичний розподіл молекул та його значення
.
Статистичний метод дослідження термодинамічних систем заснований на конкретних уявленнях про структурні елементи, з яких система складається (молекул); з уявлень про їх природу, про характер їх рухів. Але тому що елементів дуже багато, динамічні характеристики їх руху, руху молекул, позбавлені фізичного змісту, - тобто з ними не можна оперувати, - фізичний зміст мають тільки середні значення цих характеристик. Одне з основних положень статистичної теорії, так звана ергодична аксіома
, або, інколи, ергодична теорема, стверджує, що середнє історичне
значення динамічної характеристики, тобто середнє за часом існування, для кожної молекули, співпадає з середнім статистичним
, тобто з середнім значенням даної характеристики, розрахованому по всіх молекулах системи. Виконуються спроби довести це твердження як теорему, але поки що певні докази відсутні. Середні статистичні значення характеристик розраховуються за методами математичної статистики, тому теорія називається статистична фізика
. При розгляді руху термодинамічної системи в цілому встановлюються зв’язки між середніми значеннями характеристик окремих молекул та термодинамічними параметрами стану системи в цілому, як це відтворює основне рівняння молекулярно-кінетичної теорії (5.13), наприклад.
Познайомимося з методами математичної статистики та з прийомами розрахунку середніх статистичних значень динамічних характеристик.
Статистичний метод оперує з випадковими подіями
та випадковими величинами
. Випадковими називаються події, які можуть відбуватися або не відбуватися за одних і тих саме умов досліду. Наприклад, при підкидання монети може випадати орел чи решітка, при роздачі гральних карт випасти та чи інша карта, гральні кості випадати тим чи іншим числом очок і таке інше. Кількісно можливість реалізації випадкової події А
характеризується ймовірністю
або математичним очікуванням Р(А)
. Ймовірність події А
визначається за частотним або часовим фактором:
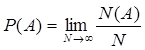 або або 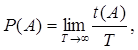 (6.1) (6.1)
де N
іT
–
загальна кількість дослідів та загальний час дослідження, а N
(
A
)
та t
(
A
)
– відповідно кількість дослідів та тривалість часу з подією А
під час дослідження. Так для орла і решітки ймовірність дорівнює 0,5, а ймовірність випадіння туза пікового у „мар’яжі” дорівнює 1/32 і так далі. Звичайно йдеться про нескінчену кількість дослідів та нескінчений час дослідження. Під час гри може п’ять разів підряд випадати орел і таке інше. Ймовірність достеменної події приймається за одиницю
, а ймовірність події, що не може реалізуватись в даних умовах досліду, приймається за нуль
.
Випадкові події називаються взаємо виключними
, якщо реалізація однієї з них виключає можливість іншої. Сумою випадкових подій А
та В
називається складна подія коли реалізується або А
або В
. Для взаємно виключних подій ймовірність суми дорівнює сумі ймовірностей реалізації кожної з них:
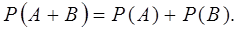 (6.2) (6.2)
Якщо реалізуються і подія А і подія В
, то кажуть про добуток подій
. Ймовірність добутку незалежних подій
дорівнює добутку ймовірностей реалізації кожної з них:
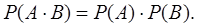 (6.3) (6.3)
Випадковою величиною
називається величина, яка може приймати ті чи інші значення в однакових умовах досліду. Випадкові величини задаються розподілом ймовірностей їх реалізації на спектрі дозволених значень величини
:
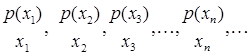 (6.4) (6.4)
Якщо спектр дозволених значень випадкової величини суцільний, то ймовірність dp
(
x
)
мати значення в межах (x
,
x
+
dx
) вважається пропорціональною величині інтервалу:
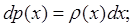 де де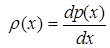 - (6.5) - (6.5)
густина ймовірності мати це конкретне значення випадкової величини х
. Випадкові величини з суцільним спектром дозволених значень задаються густиною ймовірностей їх реалізації,
яка носить назву функції розподілу
:
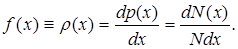 (6.6) (6.6)
Ймовірність отримати довільне з дозволених значень – це достеменна подія, тому
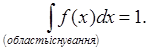 (6.7) (6.7)
Умова (6.7) називається умовою нормування
. Ймовірність мати значення випадкової величини в межах (x1
, x2
) визначається інтегралом:
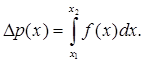 (6.8) (6.8)
Середні значення досліджуваної величини та довільної функції від неї знаходяться за такими формулами:
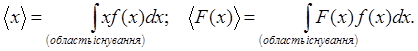 (6.9) (6.9)
Таким чином, всі відомості про систему будуть отримані, якщо відома функція розподілу (6.6). Тому в статистичній фізиці стан термодинамічної системи задається функцією розподілу
. Побудова функції розподілу є одним з головних завдань статистичної фізики. Вона будується, як правило, виходячи з загальних міркувань, теорії математичної статистики та конкретних припущень про природу та характер руху структурних елементів системи. В залежності від природи „молекул” системи існує класична статистика
– для класичних молекул, та квантова статистика
– для термодинамічних систем з квантових об’єктів.
2 Максвелівський розподіл молекул за швидкостями. Середньостатистичні значення швидкостей руху молекул та їх взаємозв’язок
Функцію розподілу молекул ідеальних класичних газів рівноважної термодинамічної системи вперше поставив та розв’язав англійський дослідник Дж. Кл. Максвел в 1859 році.
Розглядається рівноважний стан ідеального газу
, що не знаходиться під дією зовнішніх сил. Параметри стану, в тому числі і концентрація молекул у всіх точках системи однакові
. Рух молекул абсолютно хаотичний, всі напрямки руху молекул абсолютно рівноправні, проекції швидкостей руху молекул незалежні одна від одної
. Після встановлення рівноважного хаотичного руху процесами взаємного зіткнення молекул можна нехтувати. Останнє положення Максвелом приймалось на віру і було обґрунтоване теоретично пізніше Л.Больцманом.
Виходячи з таких положень Максвел, використовуючи методи математичної статистики, отримав функції розподілу молекул за проекціями швидкостей:
 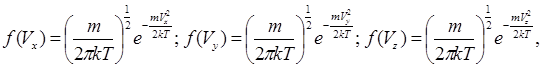 (6.10) де (6.10) де 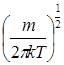 є нормуючий коефіцієнт. є нормуючий коефіцієнт.
Виходячи з положення про незалежність проекцій швидкостей, та з положення теорії ймовірностей про множення ймовірностей випадкових величин (6.3), отримаємо функцію розподілу молекул за швидкостями (тобто густину ймовірності мати конкретне значення вектора швидкості, або одночасно мати всі три проекції швидкості):
 (6.11) (6.11)
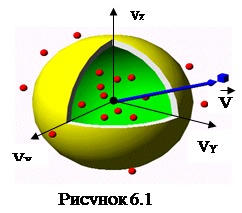
На практиці дослідника цікавить розподіл за модулями швидкостей
, що і носить назву максвелівського розподілу або розподілу молекул за швидкостями
. Для переходу від розподілу молекул за проекціями швидкостей до розподілу за модулями швидкостей використовується положення про рівноправність всіх напрямків руху молекул та прийом, пов’язаний з використанням так званих фазових просторів зображення стану рівноважної термодинамічної системи, де кожна точка фазового простору. У загальному випадку це 6
N
-мірний простір координат та імпульсів (або швидкостей), де N
– загальна кількість молекул. У конкретному випадку розгляду рівноважного ідеального газу не підлеглого впливу зовнішніх сил, фазовий простір зводиться до тривимірного простору швидкостей. У такому просторі кожна точка визначає швидкість молекул  (рис. 6.1).Поряд з вектором швидкості (рис. 6.1).Поряд з вектором швидкості  на рис. 6.1 зображено елементарний кубик із сторонами dVx
, dVx
, dVx
, що містить dNмолекул, швидкості яких знаходяться в його межах. Густина цих молекул на рис. 6.1 зображено елементарний кубик із сторонами dVx
, dVx
, dVx
, що містить dNмолекул, швидкості яких знаходяться в його межах. Густина цих молекул

являє собою функцію розподілу за векторами швидкостей. Зважаючи на абсолютну хаотичність руху молекул розглядуваного газу та на рівноправність всіх напрямків їх руху, можна стверджувати, що густина молекул у всіх точках (виділеного на рис. 6.1l двома вставленими одна в одну сферами радіусами Vта V+dV) сферичного шару, модулі швидкостей для якого знаходяться в межах (V,V+dV), одна і та ж саме:
 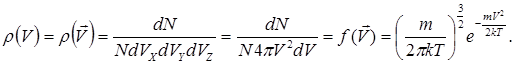 (6.12) (6.12)
Таким чином, функція розподілу молекул за швидкостями
по їх модулях
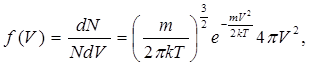 (6.13) (6.13)
як це слідує із співвідношення (6.12).
 Співвідношення (6.13) представляє собою максвелівський розподіл молекул за швидкостями
. Графік функції максвелівськогорозподілу Співвідношення (6.13) представляє собою максвелівський розподіл молекул за швидкостями
. Графік функції максвелівськогорозподілу представлений на рис. 6.2.
На рис. 6.2 а представлений загальний вид графіка функції Максвела, а на рис. 6.2 б демонструється залежність ходу функції від температури газу. Т1
<T2
<T3
. Як це слідує з умови нормування (6.7), площа під графіком, тобто  а ймовірність мати швидкості в межах від V1
до V2
визначається як а ймовірність мати швидкості в межах від V1
до V2
визначається як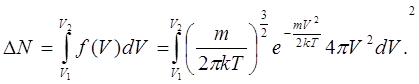 (6.14) (6.14)
Якщо температура газу зростає до нескінченості функція розподілу співпаде з віссю швидкостей, тобто всі швидкості від нуля до нескінчено великої будуть рівно представлені. Навпаки, коли температура газу прагнутиме до абсолютного нуля, швидкості всіх молекул стануть нульовими. Найбільш ймовірною швидкістю є швидкість V
в
,
що відповідає максимуму функції (6.13) (див. рис. 6.2). Дослідження на максимум функції (6.13) дає результат:
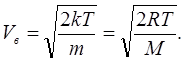 (6.15) (6.15)
Середня арифметична швидкість та квадрат середньої квадратичної швидкостей знаходяться за формулами (6.9):
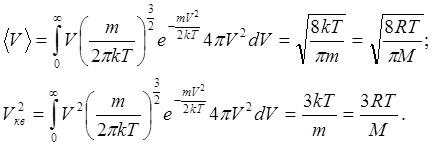 (6.16) (6.16)
Середня квадратична швидкість, як це випливає з другого співвідношення (6.16):
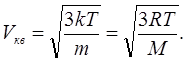 (6.17) (6.17)
Всі ці три статистичні характеристики представлені на рис. 6.2 і відносяться між собою як
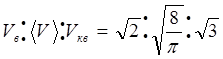 . (6.18) . (6.18)
3 Барометрична формула. Досліди Перена з визначення числа Авогадро. Класичний розподіл молекул за енергіями
Закон, що встановлює загальній розподіл рівноважного ідеального газу за енергіями був теоретично побудований австрійським фізиком Людвігом Больцманом в 1866 році. Формула рівноважного больцманівського розподілу лягла в основу класичної статистичної фізики. Не вдаючись в складні викладки зроблені Больцманом, ми зможемо записати закон розглянувши розподіл молекул рівноважної термодинамічної системи, що знаходиться під впливом зовнішнього потенціального силового поля, поля сили земного тяжіння, наприклад. Цей підхід має самостійне значення, тому що дозволяє встановити розподіл концентрації молекул повітря та тиску атмосфери по висоті. Взагалі кажучи, стовп атмосфери має різну температуру по висоті підняття над поверхнею Землі. Але взявши середню температура за 250 К маємо зміни температури від 200 К до 300 К тобто DT=±50К або 20% в верхніх шарах атмосфери та біля поверхні Землі. Для отримання теоретичної залежності будемо вважати атмосферу рівноважним ідеальним газом з молекулярною масою 29 г/моль
, що знаходиться під дією поля сил тяжіння.
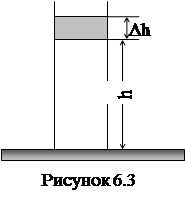
Виділимо елемент висоти стовпа повітря dh, що відповідає зміні тиску на dp (рис. 6.3):
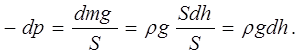 (6.19) (6.19)
Для отримання інтегральної форми звернемо увагу на те, що в виразі (6.19) три змінні величини. Зменшимо кількість змінних скориставшись рівнянням стану ідеальних газів (5.10) для виразу густину повітря через тиск:
 (6.20) (6.20)
Рівняння (6.20) інтегрується розділенням змінних:
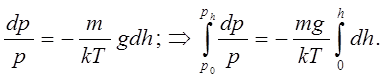
Після інтегрування маємо:
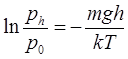 або або  (6.21) (6.21)
де рh
та p0
відповідно тиск повітря на висоті h та біля поверхні Землі. Формула (6.21) встановлює залежність тиску повітря від висоти підняття на нульовим рівнем і носить назву барометричної формули
. Скориставшись рівнянням стану ідеальних газів у формі (5.11), барометричну формулу можна переписати для залежності концентрації молекул від висоти підняття над нульовим рівнем:
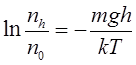 або або 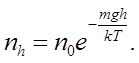 (6.22) (6.22)
Якщо температура атмосфери планети прагне до нескінченості, тиск та концентрація молекул повітря не залежать від висоти, молекули рівномірно розподіляться по висоті, атмосфера залишить планету. Навпаки, якщо температура атмосфери прагне до нуля всі молекули повітря ляжуть на нульовий рівень. Звісно йдеться про теоретичні можливості, що випливають з барометричної формули.
Використання барометричної формули дало можливість французькому досліднику Жану Батисту Перену в 1909 році експериментально визначити число Авогадро. В дослідах Перена вивчався розподіл концентрації дрібнодисперсних часток смоли гумігуту в воді. Тому що використовувались не молекули а частинки значно більших розмірів, замість маси необхідно було брати до уваги ефективну масу з врахуванням виштовхувальної сили  , де r
, r
0
відповідно густина речовини гумігуту і води, а
– діаметр частинок. Таким чином , де r
, r
0
відповідно густина речовини гумігуту і води, а
– діаметр частинок. Таким чином
 (6.23) (6.23)
Звідки
 (6.24) (6.24)
Концентрація часток в шарах емульсії та відстань між ними h
вимірювалась за допомогою мікроскопа.
В дослідах Перена змінювались температура та розмір зерен частинок емульсії. У всіх дослідах значення постійної Авогадро отримано близьким до 6,8·1023
моль-1
, що непогано співпадає з сучасним значенням цієї константи.
Якщо зважити на те що mgh
=
Еп
– потенціальна енергія молекул повітря в полі сили тяжіння, то барометричну формулу (6.22) можна переписати у вигляді, що дає розподіл молекул у потенціальному полі:
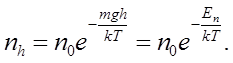 (6.25) (6.25)
Больцмана показав, що такий закон має місце для розподілу концентрації молекул ідеальних газів в довільному потенціальному полі. Він також довів, що розподіл (6.11) виконується в мікро об’ємах рівноважних газів, що знаходяться в зовнішніх потенціальних полях. Зважаючи на той факт, що 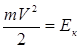 та на незалежність розподілів молекул за кінетичною та за потенціальною енергіями, можна стверджувати, що функція розподілу молекул рівноважного ідеального газу за енергіями та на незалежність розподілів молекул за кінетичною та за потенціальною енергіями, можна стверджувати, що функція розподілу молекул рівноважного ідеального газу за енергіями
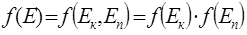 
де А
– постійна величина, що знаходиться з умови нормування (6.7). Функція
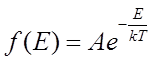 (6.26) (6.26)
репрезентує закон розподілу молекул рівноважного класичного ідеального газу за енергіями, розподіл Больцмана
.
1
Термодинамічна система. Внутрішня енергія термодинамічної системи. Робота та кількість теплоти. Перший закон термодинаміки.
2
Теплоємність тіл. Застосування першого закону термодинаміки до ізопроцесів. Теплоємність ідеальних газів в ізопроцесах
.
3
Адіабатичний процес. Внутрішня енергія та робота в адіабатичному процесі. Рівняння Пуасона.
1 Термодинамічна система. Внутрішня енергія термодинамічної системи. Робота та кількість теплоти. Перший закон термодинаміки
Термодинамічний метод, як на це було вказано вище, досліджує термодинамічні системи не цікавлячись їх будовою. З точки зору термодинаміки термодинамічною системою
називається макроскопічна система, що вивчається методами термодинаміки. Всі тіла, не включені в термодинамічну систему, називаються зовнішнім середовищем
.
Основним поняттям при вивченні термодинамічних систем є внутрішня енергія
. Перший закон термодинаміки стверджує
: існує внутрішня енергія термодинамічної системи
- така однозначна функція параметрів її стану, зміна якої дорівнює роботі, виконаної над системою
та кількості підведеної теплоти
.
Робота і теплота це дві форми зміни внутрішньої енергії термодинамічних систем. Роботою
називається фізична величина, що характеризується зміною внутрішньої енергії термодинамічної системи за рахунок переміщень макрочастин системи або всієї системи в цілому. В подальшому розглядається тільки такі процеси, в яких внутрішня енергія визначається тільки її внутрішнім станом. Кількість теплоти
це фізична величина, що є мірою зміни внутрішньої енергії в процесах, що не супроводжуються виконанням роботи, в процесах де хаотичний рух переходить від одних тіл в хаотичний рух інших, від однієї частини системи до іншої без виконання роботи.
Молекулярна фізика дає тлумачення внутрішньої енергії
як суми кінетичних енергій всіх молекул та потенціальної енергії їх взаємодії. В подальшому розглядаються тільки такі процеси, в яких не відбувається перетворень молекул, атомів або їх ядер. Енергія, як завжди, визначається з точністю до адитивної константи, тому всі види енергії вказаних джерел вводяться в константу, яка приймається нульовою. Внутрішня енергія ідеальних газів складається тільки з кінетичної енергії руху молекул і дорівнює [див. рівність (5.20)]
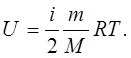 (7.1) (7.1)
В термодинаміці внутрішню енергію частіше позначають літерою U
, тому приймемо його. Кількість теплоти та робота відповідно позначаються літерами Q
таA
.
За звичаєм під роботою розуміють роботу виконану не над системою, а системою проти зовнішніх сил. Тому перший закон термодинаміки
стверджує, що кількість підведеної до термодинамічної системи теплоти витрачається на зміну її внутрішньої енергії та на роботу проти зовнішніх сил:
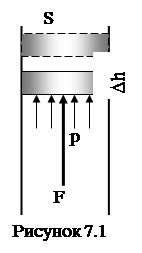  (7.2) (7.2)
Робота ідеального газу проти зовнішніх сил пов’язана тільки із зміною об’єму. Дійсно (див. рис 7.1), робота сили внутрішнього тиску газу
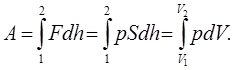 (7.3) (7.3)
Робота на діаграмі „р‑V” зображається площею під графіком функції p(V) (див. рис 5.1 a).
Внутрішня енергія є однозначною функцією стану системи, тому нескінчено мала її зміна є повним диференціалом dU
.
Робота та кількість теплоти, навпаки, залежать від форми переходу між станами і не є повними диференціалами, тому це dА та dQ. Диференціальна форма першого закону термодинаміки записується так:
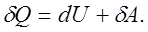 (7.4) (7.4)
2 Теплоємність тіл. Застосування першого закону термодинаміки до ізопроцесів. Теплоємність ідеальних газів в ізопроцесах
Досвід вчить, що кількість теплоти, підведеної до системи, прямо пропорційна різниці температур системи:
Q = С (Т2
- Т1
)
(7.5)
де Т1
- початкова, а Т2
- кінцева температури системи; С
- постійний для системи коефіцієнт, що носить назву теплоємності системи. Якщо система є однорідне тіло, її теплоємність пропорційна масі тіла:
С = с m,
(7.6)
де с
- питома теплоємність речовини тіла: m
- маса тіла; а також пропорційна кількості речовини тіла:
С = См
n
, (7.7)
де См
- молярна теплоємність речовини тіла, а n
кількість молів речовини тіла,
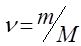 , (7.8)
, (7.8)
де m
- маса тіла; M -
молярна маса речовини.
Таким чином,
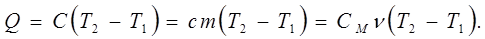 (7.9) (7.9)
Відповідно до рівняння (7.9) теплоємності тіла визначаються за такими формулами:
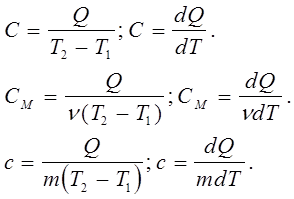 (7.10) (7.10)
Розглянемо особливості застосування першого закону термодинаміки до ізопроцесів в ідеальних газах.
Класична теорія теплоємності базується на теоремі про рівномірний розподіл енергії по ступенях свободи термодинамічної системи яка дозволяє обчислити внутрішню енергію ідеального газу [див. формулу (7.1)].
Робота ідеального газу проти зовнішніх сил зводиться тільки до роботи зміни його об’єму [див. формулу (7.3)]:
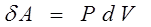 і і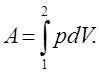 (7.11) (7.11)
Робота зміни об’єму ідеального газу залежить від виду газового процесу, тому елементарна робота d
А
не є повним диференціалом.
В ізохорному процесі V
= const
, тому d
А
=
РdV
=
0
і
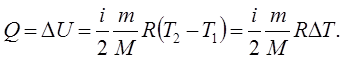 (7.12) (7.12)
В ізотермічному процесі Т
= const
, тому D
U
= 0
і
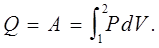 (7.13) (7.13)
В підінтегральному виразі є дві змінні. Скориставшись рівнянням стану ідеального газу (5.8), виразимо, наприклад, Р
через об’єм V
і одержимо:
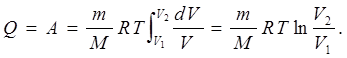
Відомо, що ізотермічний процес підкоряється закону Бойля-Маріотта:
P1
V1
= P2
V2
, тому для нього
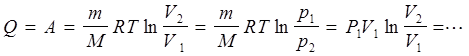 (7.14) (7.14)
В ізобарному процесі Р = const
, тому для нього
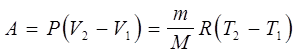 (7.15) (7.15)
і перший закон термодинаміки (7.10) з урахуванням рівняння (7.11) має вигляд:
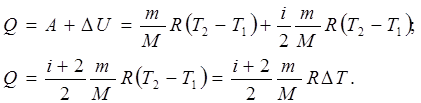 (7.16) (7.16)
Всі ізопроцеси досліджені для незмінної маси ідеальних газів:
m = const; М = const
.
Відповідно до визначення теплоємностей (7.10) і співвідношень (7.13), (7.14), (7.16) для теплоємностей ідеальних газів маємо:
а) для ізохоричного процесу -
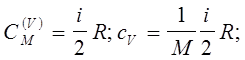 (7.17) (7.17)
б) для ізотермічного процесу теплоємність не визначена і прямує до нескінченності -
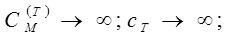 (7.18) (7.18)
в) для ізобарного процесу -
 (7.19) (7.19)
3. Адіабатичний процес. Внутрішня енергія та робота в адіабатичному процесі. Рівняння Пуасона
Крім названих вище процесів в термодинаміці до ізопроцесів відносять адіабатичний процес. Адіабатичним
називається процес
, що відбувається без теплообміну з довколишніми тілами. Для нього d
Q = 0
і
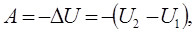 (7.20) (7.20)
тобто робота проти зовнішніх тіл відбувається за рахунок внутрішньої енергії. Для ідеального газу
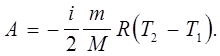 (7.21) (7.21)
Якщо роботу виконує система (А
>
0)
- вона охолоджується (Т2
<
T1
); якщо роботу в адіабатичному процесі виконують зовнішні сили над системою (А
<
0)
- система розігрівається (Т2
>
Т1
)
. В диференціальній формі перший закон термодинаміки для адіабатичного процесу записується так:
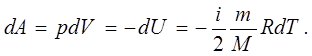 (7.22) (7.22)
Для отримання рівняння, що зв’язує параметри адіабатичного процесу, скористаємося диференціальною формою першого закону термодинаміки (7.22) та рівнянням стану ідеальних газів (5.8):
 (7.23) (7.23)
і поділимо ці співвідношення окремо ліві та праві частини:
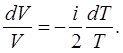 (7.24) (7.24)
Рівняння (7.24), як відомо, після інтегрування і потенціювання дає результат:
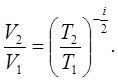 (7.25) (7.25)
Взагалі кажучи, інтегрування рівняння (7.24) повинно відбуватись з точністю до постійної інтегрування, яка, як це доводиться, може бути нульовою.
За домовленістю, в рівнянні (7.25) замість кількості ступіней вільності вживається інша величина, яка визначається як відношення теплоємностей в ізобарному та ізохорному процесах:
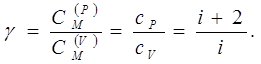 (7.26) (7.26)
Відповідно, рівняння (7.25) приймає форму
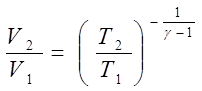 або або 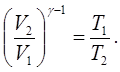 (7.27) (7.27)
Отримане рівняння носить назву рівняння Пуасона. Воно може бути представленим в інших формах шляхом використання об’єднаного газового закону (5.6):
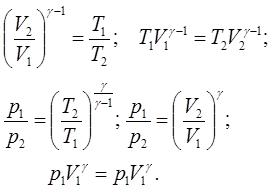 (7.28) (7.28)
Теплоємність тіла в адіабатичних процесах дорівнює нулю.
 Теоретичне значення відношення молярних (і питомих) теплоємностей для ідеальних газів (7.26) може бути розрахованим. Наприклад, повітря складається в основному з молекул двохатомних газів N2
, О2
, Н2
і таке інше, тому для повітря кількість ступенів свободи і = 5
: три поступального і дві обертального рухів. Теоретичне значення відношення молярних (і питомих) теплоємностей для ідеальних газів (7.26) може бути розрахованим. Наприклад, повітря складається в основному з молекул двохатомних газів N2
, О2
, Н2
і таке інше, тому для повітря кількість ступенів свободи і = 5
: три поступального і дві обертального рухів.
Вважається, що молекули повітря жорсткі диполі, тобто дві матеріальні точки жорстко зв’язані між собою (рис. 7.2).
Центр мас цієї системи має 3 координати (х, у, z ) - поступальні ступені свободи; система може обертатись довкола осей Ох і Оz - два ступеня свободи. Обертанням довкола власної осі (вісь Оу) нехтуємо, тому що атоми вважаються матеріальними точками. Відповідно для повітря теоретичне значення відношення теплоємності при постійному тиску до теплоємності при постійному об’ємі g
= 1,4
.
 Графік адіабатичного процесу ідеальних газів, що носить назву адіабати
(рис. 7.3) іде більш круто ніж ізотерма. Графік адіабатичного процесу ідеальних газів, що носить назву адіабати
(рис. 7.3) іде більш круто ніж ізотерма.
1
Термодинамічні процеси. Оборотні та необоротні процеси. Колові процеси (цикли). Коефіцієнт корисної дії (ККД) циклу.
2
Цикл Карно та його ККД. Зведена теплота. Ентропія. Вільна та зв’язана частини внутрішньої енергії.
3
Теорема Карно. Другий закон термодинаміки. Абсолютна термодинамічна шкала температур.
4
Статистичне тлумачення ентропії та другого закону термодинаміки. Нерівність Клаузиуса та критика теплової смерті всесвіту.
1 Термодинамічні процеси. Оборотні та необоротні процеси. Колові процеси (цикли). Коефіцієнт корисної дії (ККД) циклу
Формульовка другого закону термодинаміки відбулася раніше ніш першого і пов’язана з іменем Саді Карно (1824 р.) та вивченням роботи теплових двигунів, що мають циклічну форму роботи. Тому, перш ніж перейти до формулювання другого закону познайомимося з особливостями термодинамічних процесів та циклів.
Перехід термодинамічної системи між станами називається термодинамічним процесом
. Якщо перехід відбувається через проміжні рівноважні стани, він називається квазістатичним
і його можна зображати графічно на термодинамічних діаграмах (див., наприклад, рис. 5.1, 5.2, 5.3). Термодинамічний процес називається оборотним
, якщо після його закінчення термодинамічну систему і всі оточуючі тіла можна повернути у вихідний стан таким чином, щоб в оточуючих тілах не виникло будь яких змін. Процес, що не відповідає таким вимогам , називається необоротним
. Звичайно, йдеться про модельні ідеалізовані процеси. Реальні процеси необоротні.
Коловими процесами,
або циклами
, називається така сукупність термодинамічних процесів, в результаті яких система повертається у вихідний стан. Квазістатичні колові процеси можуть зображатись графічно на термодинамічних діаграмах. Приклад рівноважного колового процесу 1a
2b1 представлено на діаграмі „p ‑ V” рис. 8.1.
Тіло, що виконує коловий процес та обмінюється енергією з оточуючими тілами називається робочим тілом
. Для того, щоб робоче тіло могло виконувати роботу, необхідно мати, як на це вказує досвід, нагрівач
для відбору від нього теплоти, та холодильник
, як необхідний елемент компенсаційного процесу для повернення робочого тіла у вихідний стан. За один цикл робоче тіло отримує від нагрівача деяку кількість теплоти Q1
, виконує роботу А і віддає холодильнику кількість теплоти Q2
.
За першим законом термодинаміки для процесу отримання теплоти 1а
2
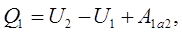 (8.1) (8.1)
де U
1
таU
2
- внутрішня енергія робочого тілі відповідно у першому та другому станах; А
1а
2
– робота виконана робочим тілом проти зовнішніх сил в процесі забору тепла від нагрівача, вона зображається на рис. 8.1 площею фігури 1а
2341. Для процесу віддачі теплоти холодильнику 2b
1 кількість забраної від робочого тіла теплоти
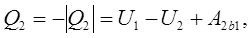 (8.2) (8.2)
де А
2
b
1
– робота виконана надробочим тілом в процесі забору тепла від робочого тіла холодильником, вона зображається на рис. 8.1 площею фігури 2b1432.
Якщо скласти рівності (8.1) та (8.2) одержимо вираз для обчислення роботи, виконаної робочим тілом за один цикл:
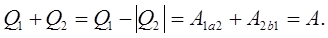 (8.3) (8.3)
На рисунку (8.1) робота А представлена площею заштрихованої поверхні, охопленої графіком циклу.
Коефіцієнт корисної дії (ККД) циклу
визначається відношенням виконаної роботи до підведеної до робочого тіла теплоти за один цикл:
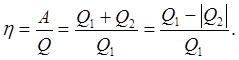 (8.4) (8.4)
ККД (h) циклу носить назву термічного
, він характеризує економічність циклу теплової машини
.
Існують також холодильні машини
, які працюють за зворотним циклом – їх призначення забирати тепло Q
2
у робочого тіла та, виконавши роботуA¢над робочим тілом, віддавати частину тепла 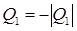 зовнішньому середовищу. Тому холодильний коефіцієнт зворотного циклу зовнішньому середовищу. Тому холодильний коефіцієнт зворотного циклу
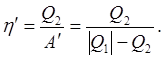 (8.5) (8.5)
2 Цикл Карно та його ККД. Зведена теплота. Ентропія. Вільна та зв’язана частини внутрішньої енергії
Модельним рівноважним оборотним циклом є цикл Карно, запропонований французьким дослідником Саді Карно в 1824 році. Цикл Карно зіграв вирішальну роль у розвитку термодинаміки та теплотехніки, він дозволив вирішити питання про визначення ККД теплових машин. Виходячи із неможливості створення вічного двигуна, Карно показав, що корисну роботу можна отримати тільки тоді коли тепло переходить від більш нагрітого тіла до менш нагрітого. Труди Карно отримали широку відомість в 1834 році коли Клапейрон надав його ідеям доступну математичну форму.

Прямий цикл Карно
(рис. 8.2) складається з двох ізотерм: 1®2 за температури Т1
і 3®4 за температури Т2
та двох адіабат: 2®3 і 4®1.
В ізотермічному процесі 1®2 робоче тіло знаходиться в прямому контакті з нагрівачем за температури Т1
та забирає від нього кількість тепла Q
1
. В точці 2 припиняється тепловий контакт з нагрівачем, робоче тіло ізолюється і в адіабатичному розширенні робочого тіла продовжує виконуватись робота за рахунок запасеної внутрішньої енергії робочого тіла. В точці 3 робоче тіло знову приводиться в прямий тепловий контакт але уже з холодильником за температури Т2
. В ізотермічному процесі 3®4 холодильник відбирає від робочого тіла кількість теплоти Q
2
. В точці 4 припиняється тепловий контакт з холодильником, робоче тіло знову ізолюється і в адіабатичному процесі 4®1 виконується робота стискування робочого тіла. При цьому температура робочого тіла зростає і в точці 1 робоче тіло знову матиме температуру Т1
. Цикл закінчено, робоче тіло знову ізолюється і приводиться в контакт з нагрівачем – цикл може повторюватись. Для дослідження ККД циклу Карно в якості робочого тіла приймемо ідеальний газ. Термічний ККД [див. формулу (8.4)]такого циклу Карно визначається кількостями теплот, отриманої та відданоїв ізотермічних процесах ідеального газу:
 (8.6) (8.6)
Скористаємося рівнянням Пуассона (7.25) з якого слідує, що
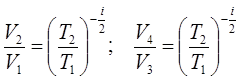 , тобто , тобто  і, таким чином, і, таким чином, 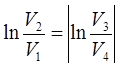 . .
Підстановка останнього виразу в рівняння (8.6) для ККД дає результат:
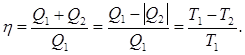 (8.7) (8.7)
Таким чином коефіцієнт корисної дії циклу Карно
, з ідеальним газом в якості робочого тіла, залежить тільки від температур нагрівача та холодильника.
Цикл Карно має принципове значенняу розумінні термодинамічних процесів ще і тому, що довільний рівноважний оборотний цикл може бути представленим як суперпозиція циклів Карно, як це видно з рис. 8.3. Кожна ізотерма та кожна адіабата внутрішніх циклів Карно обходиться двічі в протилежних напрямках для сусідніх циклів. Таким чином всі внутрішні цикли взаємно знищуються і, при збільшенні кількості внутрішніх циклів до нескінченості, залишається тільки зовнішня оболонка досліджуваного циклу.
Аналіз виразу для ККД циклу Карно дозволяє ввести ентропію
яка є, наряду з внутрішньою енергією, ще однією однозначною функцією параметрів стану термодинамічної системи. Введення ентропії пов’язане з поняттям зведеної
теплоти, величини що дорівнює відношенню кількості теплоти, отриманої в ізотермічному процесі до температури процесу:
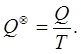 (8.8) (8.8)
Сума зведених теплот оборотного циклу Карно дорівнює нулю. Дійсно, перепишемо вираз для ККД циклу (8.7) в іншому вигляді:
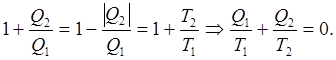 (8.9) (8.9)
Зважаючи на те, що зведені теплоти 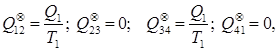 та співставивши їх з виразом (8.9), отримаємо що та співставивши їх з виразом (8.9), отримаємо що
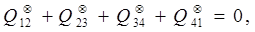 (8.10) (8.10)
де враховано, що в адіабатичних процесах „2®3” та „4®1” кількість підведеної теплоти і, відповідно, зведені теплоти дорівнюють нулю.
Тому, що довільний оборотний цикл можна представити як нескінчену сукупність оборотних циклів Карно, можна записати, що
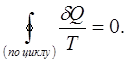 (8.11) (8.11)
Рівність нулю інтеграла (8.11) означає, що підінтегральний вираз є повним диференціалом деякої однозначної функції параметрів стану термодинамічної системи:
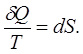 (8.12) (8.12)
ВеличинаS
називається ентропією термодинамічної системи.
Це така однозначна функція параметрів термодинамічної рівноважної системи, зміна якої дорівнює сумі зведених теплот у відповідному рівноважному процесі
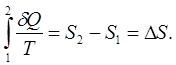 (8.13) (8.13)
Ентропія величина суто скалярна. Тому що введена через різницю вона обчислюється з точністю до довільної константи; має розмірність  В ізотермічних процесах, наприклад танення льоду та випаровування води при кипінні це відповідно В ізотермічних процесах, наприклад танення льоду та випаровування води при кипінні це відповідно
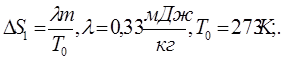 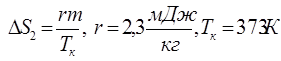 . .
В процесах нагрівання ентропія зростає, в процесах остигання – зменшується.
Для вияснення фізичного змісту ентропії скористаємось записом (7.4) диференціальної форми першого закону термодинаміки та виразом 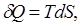
що випливає з визначення (8.12):
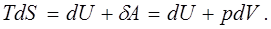 (8.14) (8.14)
Зважаючи на те, що  маємо маємо

і, підставивши його в вираз (8.14), отримаємо
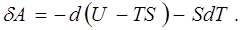 (8.15) (8.15)
В співвідношенні (8.15) фігурує ще одна однозначна функція параметрів стану рівноважної термодинамічної системи
 (8.16) (8.16)
яка називається вільною енергією
, тому що визначає собою ту частину внутрішньої енергії термодинамічної системи яка максимально може бути перетвореною у роботу. Таке трактування вільної енергії стає зрозумілим, якщо рівняння (8.15) примінити до ізотермічного процесу, в якому вся теплота переходить у роботу [див. рівняння (7.13)], тобто виконується максимально можлива робота за рахунок теплоти. Дійсно, примінимо вираз (7.14) до ізотермічного процесу 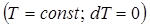 , в якому вся теплота переходить в роботу [див. вираз (7.13)], тобто виконується максимально можлива робота за рахунок теплоти: , в якому вся теплота переходить в роботу [див. вираз (7.13)], тобто виконується максимально можлива робота за рахунок теплоти:
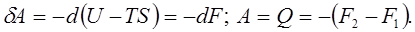 (8.17) (8.17)
Відповідно, з виразу (8.16) слідує, що ентропія визначає собою ту частину внутрішньої енергії, яка ніколи не може бути перетвореною в корисну роботу
. Тобто ентропія визначає собою частину знеціненої внутрішньої енергії термодинамічної системи
. В цьому полягає її значення.
4. Теорема Карно. Другий закон термодинаміки. Абсолютна термодинамічна шкала температур.
   
З введенням ентропії можна довести важливе положення термодинаміки, що носить назву теореми Карно
, яка стверджує що термічний ККД оборотного циклу Карно не залежить від природи робочого тіла і визначається тільки температурами нагрівача та холодильника
. Для доведення теореми Карно скористаємося діаграмою „T-S” (рис. 8.4), в якій цикл Карно не залежно від природи робочого тіла зображається у вигляді прямокутника 1®2®3®4®1.
  З визначення ентропії (8.12) слідує, що З визначення ентропії (8.12) слідує, що 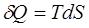 . Кількість теплоти, отриманої в ізотермічному процесі 1®2 . Кількість теплоти, отриманої в ізотермічному процесі 1®2 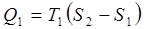 та переданої холодильнику в процесі 3®4 та переданої холодильнику в процесі 3®4 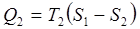 . Робота, виконана робочим тілом в циклі Карно . Робота, виконана робочим тілом в циклі Карно 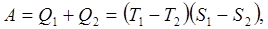 тобто зображається площею заштрихованого прямокутника. Відповідно ККД циклу: тобто зображається площею заштрихованого прямокутника. Відповідно ККД циклу:
 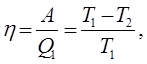 (8.18) (8.18)
що повністю співпадає з виразом (8.7) і доводить, що ККД оборотного циклу Карно не залежить від природи робочого тіла і тим саме доводить теорему Карно.
Довільний оборотний цикл, виконаний при максимальній температурі Тmax
та мінімальній Тmin
представляється деяким циклом, графік якого зображено пунктирною лінією з своєю штриховкою внутрі графіка відповідного циклу Карно. Як це показав Карно,та як це слідує із співставлення цих графіків, ККД довільного оборотного циклу не може перевищувати ККД циклу Карно:
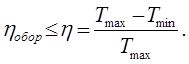 (8.19) (8.19)
Приймемо без доведення також висновок, що термічний ККД довільного необоротного циклу, що виконується між двома джерелами теплоти з температурами Т
max
та Tmin
завжди менше ККД відповідного оборотного циклу:
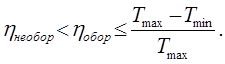 (8.20) (8.20)
Перший закон термодинаміки за своїм змістом є закон збереження і перетворення енергії в теплових процесах.
Він відповідає на питання скільки куди і в якій кількості та якості передано внутрішньої енергії термодинамічної системи. Але він не дає відомостей про направленість протікання процесів. Таку відповідь дає другий закон термодинаміки.
Існують декілька якісних формулювань другого закону термодинаміки
які є рівноцінними та випливають одне з одного:
1
Неможлива самодовільна передача теплоти від тіла менше нагрітого до тіла більше нагрітого.
(Р. Клаузиуса)
2
Неможливий замкнений процес, єдиним результатом якого було б виконання роботи за рахунок охолодження одного тіла або неможливий вічний двигун другого роду
(
perpetuum
mobile
II
)
, тобто двигун що міг би працювати, наприклад, за рахунок споживання внутрішньої енергії світового океану без холодильника. (В. Томсон, М. Планк)
3
Неможливо створити цикл, ККД якого був би рівним або більшим за сто відсотків.
Перше формулювання є майже очевидним і підтверджується практикою та досвідом. В холодильних машинах тепло передається від менш нагрітих тіл до більш нагрітих, але це відбувається за рахунок роботи супутнього процесу, а не самодовільно. Відносно другого формулювання необхідно відмітить, що в ізотермічному процесі все тепло перетворюється в роботу, але замкненим ізотермічний процес не може бути.
Друге формулювання випливає з першого і навпаки. Дійсно, якщо б була можливість самодовільно передавати енергію від менш нагрітого тіла до більш нагрітого, то був би можливим, наприклад цикл Карно, в якому за рахунок отриманої від нагрівача за температури Т1
кількості теплоті Q1
була б виконана робота A=Q1
-½Q2
½, де Q2
- кількість теплоти, відданої холодильнику з температурою Т2
<T1.
. Після цього від холодильника теплота Q2
передається до нагрівача і робота виконується тільки за рахунок охолодження нагрівача.
Трете формулювання означає, що вся теплота повинна перетворюватись в роботу, або навіть отримана робота буде більшою за кількість отриманої робочим тілом від нагрівача теплоти, що суперечить і першому і другому формулюванням другого закону термодинаміки.
Кількісне формулювання другого закону термодинаміки
випливає із співставлення виразів (8.20) та (8.7) для коефіцієнта корисної дії циклів теплових машин:
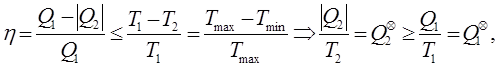 (8.21) (8.21)
тобто кількість зведеної теплоти в довільних процесах принаймні не зменшується, або залишається сталою в оборотних процесах, або збільшується в необоротних процесах. В диференціальній формі, виходячи з визначення ентропії (8.12), цей висновок можна записати так
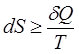 або або 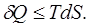 (8.22) (8.22)
Тобто теплові процеси відбуваються таким чином, що ентропія термодинамічної системи не зменшується: або залишається сталою в оборотних процесах, або збільшується в необоротних
. Нерівність (8.22) стає зрозумілою, якщо, наприклад, розглянути необоротний процес передачі теплоти від тіла з температурою Т до тіла з температурою Т-DТ. Зміна його ентропії 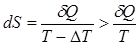 є більшою за відповідну зміну ентропії в оборотному ізотермічному процесі. є більшою за відповідну зміну ентропії в оборотному ізотермічному процесі.
З врахуванням співвідношення (8.22) для другого закону термодинаміки вираз (7.4) для першого закону термодинаміки можна переписати таким чином:
 (8.23) (8.23)
Нерівність (8.23) об’єднує обидва закони термодинаміки та є її найважнішим співвіднош
енням.
Другий закон термодинаміки разом з теоремою Карно дозволяє ввести абсолютну термодинамічну шкалу температур. Дійсно, з визначення ККД оборотного циклу Карно (8.7) слідує, що відношення температур двох тіл можна визначити через відношення кількостей теплот, якщо взяти досліджувані тіла в якості нагрівача та холодильника
:
 (8.24) (8.24)
Тому що ККД циклу Карно не залежить від природи робочого тіла, установлена таким чином шкала температур є абсолютною. Зважаючи на те що коефіцієнт корисної дії циклів не може бути 100% або більше, температура не може бути нульовою, або змінювати свій знак. В абсолютній термодинамічній шкалі температур за абсолютний нуль приймається теоретично недосяжна температура, за одиницю вимірювання приймається один кельвін (1К), що дорівнює одній сотій температурного інтервалу від потрійної точки рівноваги льоду, води та пару до точки кипіння води.
Один кельвін практично співпадає з градусом Цельсія в практичній шкалі температур. Нуль за Цельсієм відповідає 273,15 К. Абсолютний нуль відповідає температурі -273,15 °С в практичній шкалі температур.
Тому що реальні процеси є необоротними, таке визначення температур має тільки теоретичне значення.
4 Статистичне тлумачення ентропії та другого закону термодинаміки. Нерівність Клаузиуса та критика теплової смерті всесвіту
Термодинаміка тлумачить ентропію як однозначну функцію стану термодинамічної системи, що є мірою зв’язаної частини її внутрішньої енергії. Як на це було вказано в попередньому пункті. Молекулярна фізика пояснює фізичний, статистичний зміст ентропії, пов’язуючи її з станом руху структурних елементів (молекул) системи. Для формулювання таких результатів необхідно ввести поняття термодинамічної ймовірності стану системи
. Під термодинамічною ймовірністю стану термодинамічної системи розуміють кількість можливих мікророзподілень молекул, якими може бути реалізовано даний макроскопічний стан системи
. При цьому кожна з молекул має свою індивідуальність. Для пояснення візьмемо чотири молекули a, b, c, в та визначимо як вони можуть бути розподіленими в двох рівних частинах посудини відповідно до табл. 8.1.
Таблиця 8.1
| Зліва |
abcd |
abc |
abd |
acd |
bcd |
ab |
ac |
ad |
bc |
bd |
cd |
| Справа |
‑ |
d |
c |
b |
a |
cd |
bd |
bc |
ad |
ac |
ab |
Ймовірність
стану (w
)
|
1 |
4 |
6 |
Якщо всі молекули знаходяться в лівій частині посудини, а права частина пуста (або навпаки), то ймовірність реалізації такого стану дорівнює одиниці (w=1
). Якщо три молекули в лівій частині посудини, а в правій одна, то w=4
. І, нарешті, найбільша термодинамічна ймовірність стану молекул, коли вони розподілились порівну - по дві в кожній половині посудини - (w
=6). Тобто термодинамічна ймовірність характеризує ступінь хаотичності розподілу молекул системи.
Л. Больцмана довів, що ентропія термодинамічної системи зв’язана з термодинамічною ймовірністю w
її стану співвідношенням, що носить назву формули Больцмана:
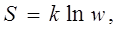 (8.24) (8.24)
де k
=1,38·10-23
Дж/К
– постійна Больцмана. Ентропія системи є мірою хаотичності руху її молекул
.
Формула Больцмана дає статистичне тлумачення другого закону термодинаміки: довільні процеси в ізольованій термодинамічні системі відбуваються таким чином, що термодинамічна ймовірність стану системи не зменшується.
Ентропія стану термодинамічної ізольованої системи та хаотичність руху її молекул при будь яких процесах в ній може тільки зростати (або залишатись незмінними, якщо процеси оборотні).
Співвідношення (8.22) носить назву нерівність Клаузиуса
. Рудольф Клаузиуса сформулював закони термодинаміки таким чином:
1) енергія Всесвіту конечна, вона нікуди не дівається, а лише перетворюється з одних видів в інші,
2) процеси у Всесвіті відбуваються таким чином, що його ентропія зростає.
А тому що зростає ентропія, частина енергії обезцінюється, хаотичність руху зростає. З часом всі види енергії перейдуть в теплову. Теплові процеси приведуть до вирівнювання температури – наступить теплова смерть Всесвіту.
Така точка зору є неправильною, тому що розповсюджувати закони термодинаміки на Всесвіт, не знаючи чи він конечний та не знаючи чи він замкнений не можна. Більше того, в термодинамічній системі можливі місцеві відхилення від рівноважного стану. Ці відхилення називаються флуктуаціями. Хоча ймовірність їх мала, але у нескінченому просторі вони можуть відігравати дуже суттєву роль. Крім того, врахування сил гравітації може сильно змінити уявлення, отримані з другого закону термодинаміки.
|