Нелокальная краевая задача для уравнения смешанного типа третьего порядка с кратными характеристиками
Езаова А.Г.
Кафедра теории функций.
Кабардино-Балкарский государственный университет
В работе рассматривается нелокальная краевая задача для уравнения смешанного типа. Поставленная задача сводится к сингулярному интегральному уравнению, которое методом Карлемана-Векуа редуцируется к интегральному уравнению Фредгольма третьего рода.
Рассмотрим уравнение
 (1) (1)
где m – натуральное число в конечной односвязной области  , ограниченной отрезками , ограниченной отрезками  прямых прямых  соответственно – и характеристиками: соответственно – и характеристиками:
 
уравнения (1).
Пусть 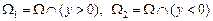 ; ;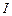 – интервал – интервал  прямой прямой 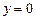 ; ;
 
– аффиксы точек пересечения характеристик уравнения (1) при  , выходящих из точки , выходящих из точки  , с характеристиками , с характеристиками  и и  соответственно; соответственно;
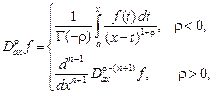 (2) (2)
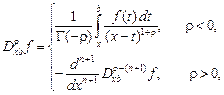 (3) (3)
– операторы дробного интегрирования порядка - при при 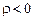 и обобщенные в смысле Лиувилля производные порядка и обобщенные в смысле Лиувилля производные порядка  при при 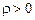 , причем , причем

где 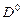 – единичный оператор, а – единичный оператор, а  – целая часть – целая часть 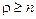 . .
Под регулярным в области  решением уравнения (1) будем понимать функцию решением уравнения (1) будем понимать функцию  , удовлетворяющую уравнению (1) в , удовлетворяющую уравнению (1) в  , и такую, что , и такую, что 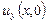 может обращаться в бесконечность порядка ниже может обращаться в бесконечность порядка ниже 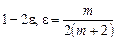 на концах А и В интервала I. на концах А и В интервала I.
Задача Н . Найти регулярное в области . Найти регулярное в области  решение решение  уравнения (1), удовлетворяющее краевым условиям: уравнения (1), удовлетворяющее краевым условиям:
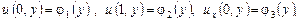  , (4) , (4)
 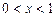 , (5) , (5)
где  , ,
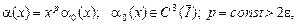 (5`) (5`)
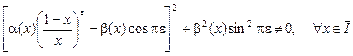 . (6) . (6)
Пусть существует решение задачи 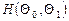 . Тогда, регулярное решение уравнения (1) в гиперболической части . Тогда, регулярное решение уравнения (1) в гиперболической части  , удовлетворяющее данным Коши , удовлетворяющее данным Коши  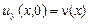 , дается формулой [1]: , дается формулой [1]:
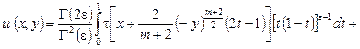
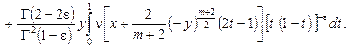 (7) (7)
Удовлетворяя (7) краевому условию (5), получим функциональное соотношение между функциями 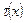 и и 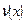 , принесенное на , принесенное на 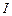 из из  [2]: [2]:
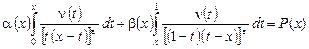 , (8) , (8)
где 
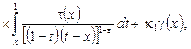 (9) (9)
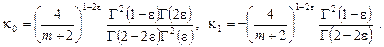 
Из постановки задачи Н следует, что функция следует, что функция 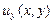 непрерывна в области непрерывна в области  . Поэтому, переходя к пределу при . Поэтому, переходя к пределу при  в уравнении (1) и учитывая граничные условия (4), получим: в уравнении (1) и учитывая граничные условия (4), получим:
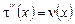 , (10) , (10)
 . (11) . (11)
Решая задачу (10), (11) относительно 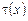 , окончательно получим функциональное соотношение между функциями , окончательно получим функциональное соотношение между функциями 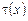 и и  , принесенное из области , принесенное из области  на на 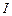 : :

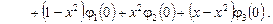 (12) (12)
Подставляя в (9) вместо функции 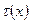 её выражение (12), получаем : её выражение (12), получаем :
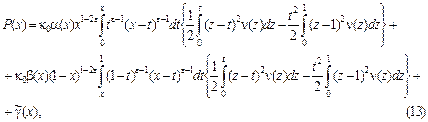
где 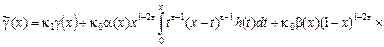
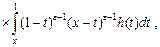
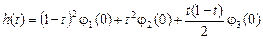 . .
Используя формулу Дирихле перестановки порядка интегрирования, перепишем равенство (13) в виде:
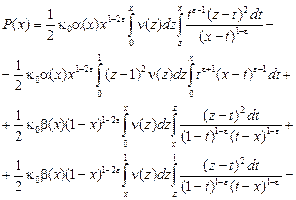
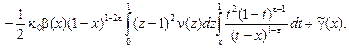 (14) (14)
Следуя [2], преобразуем интегралы:
 , , 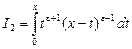 , ,  , ,
 , , 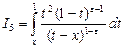 . .
В интегралах  сделаем подстановки сделаем подстановки
1) 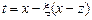 ; 2) ; 2) 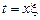 ; 3) ; 3) 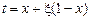 ; ;
4)  ; 5) ; 5) 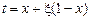
соответственно. В результате получим равенства:

 , ,
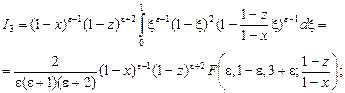
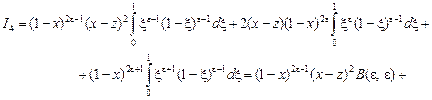 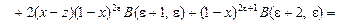
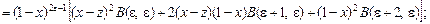
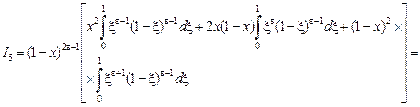
 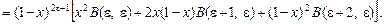
Подставляя значения  в равенство (14) и делая несложные преобразования, получаем: в равенство (14) и делая несложные преобразования, получаем:

 (15) (15)
Учитывая (15) в равенстве (7), будем иметь:

 (16) (16)
где обозначено 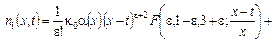
 (17) (17)
| 2 Труды молодых ученых № 3, 2007 |
|
 (18) (18)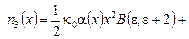
 (19) (19)
Введем вспомогательную функцию  по формуле : по формуле :

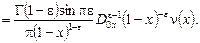 (20) (20)
Легко заметить, что функция  и в точке x=0 обращается в нуль порядка выше e, а при x=1 может обращаться в бесконечность порядка выше (1-e) относительно x и (1-x) соответственно. Из равенства (20) однозначно определяется функция и в точке x=0 обращается в нуль порядка выше e, а при x=1 может обращаться в бесконечность порядка выше (1-e) относительно x и (1-x) соответственно. Из равенства (20) однозначно определяется функция  : :
 (21) (21)
Учитывая значение функции 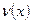 из равенства (21), в интегралах в правой части (16) получаем: из равенства (21), в интегралах в правой части (16) получаем:




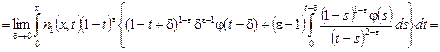



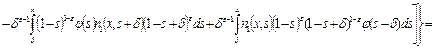 
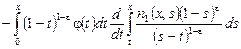 . .
Обозначим
 . (22) . (22)
Тогда окончательно имеем:
 . .
Аналогично находим, что
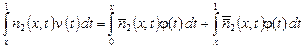 , ,
где обозначено 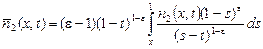 , (23) , (23)
 ; (24) ; (24)
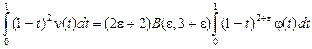 . (25) . (25)
Используя известное тождество [3],
 , ,
где интеграл понимается в смысле главного значения по Коши, уравнение (16) с учетом (5`), (17) – (19), (22) – (25) и делая несложные преобразования, приводится к сингулярному интегральному уравнению [1, 3]:

 (26) (26)
где сингулярный оператор S задаётся формулой:
 , ,
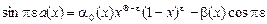 , ,  , ,
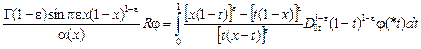 , ,
 , , 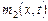 , ,  – известные функции, ограниченные соответственно на 0 £ t £ x £ 1, 0 £ x £ t £ 1, 0 £ x £ 1, причем – известные функции, ограниченные соответственно на 0 £ t £ x £ 1, 0 £ x £ t £ 1, 0 £ x £ 1, причем 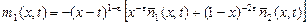 , ,  . .
Производя регуляризацию уравнения (26) по методу Карлемана – Векуа [4] и делая несложные преобразования, оно приводится к интегральному уравнению Фредгольма третьего рода [2]:
 , (27) , (27)
где 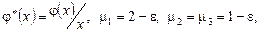 причем ядро причем ядро 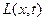 и функция и функция 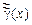 ограниченные соответственно при, 0£ x, t£ 1, 0£ x£ 1. ограниченные соответственно при, 0£ x, t£ 1, 0£ x£ 1.
Следуя [2], обозначим через 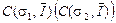 – множество функций – множество функций 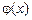 , непрерывных всюду кроме быть может точек x=0, (x=1) и удовлетворяющих условию , непрерывных всюду кроме быть может точек x=0, (x=1) и удовлетворяющих условию 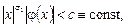 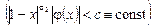 где где  , ,  – целая часть – целая часть  , , 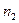 – целая часть – целая часть 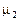 [1]. [1].
В работе [2] найдены необходимые и достаточные условия существования решения уравнения (27) в классе 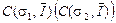 . .
Функция 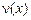 , определенная формулой (21), принадлежит классу искомых решений интегрального уравнения (8). , определенная формулой (21), принадлежит классу искомых решений интегрального уравнения (8).
После определения 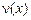 , функция , функция  задаётся формулой (12). Таким образом, в области задаётся формулой (12). Таким образом, в области  приходим к задаче [6]: найти регулярное в области приходим к задаче [6]: найти регулярное в области  решение уравнения (1), непрерывное вместе с производной решение уравнения (1), непрерывное вместе с производной  в замкнутой области в замкнутой области 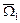 и удовлетворяющее граничным условиям (4) и и удовлетворяющее граничным условиям (4) и  . .
Решение этой задачи задается формулой :

где 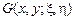 – функция Грина этой задачи для уравнения – функция Грина этой задачи для уравнения
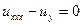 . (28) . (28)
Функция Грина выражается через фундаментальные решения уравнения (28), которые имеют вид:


где  ; ;
 ; ;
 – функция Бесселя. Функции – функция Бесселя. Функции 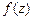 , , 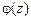 называются функциями Эйри и удовлетворяют уравнению называются функциями Эйри и удовлетворяют уравнению  . Основные свойства функций . Основные свойства функций  и и  , их оценки вместе с частными производными порядка больше 1, приведены в [7]. , их оценки вместе с частными производными порядка больше 1, приведены в [7].
Список литературы
Бицадзе А.В. Некоторые классы уравнений в частных производных. М.: Наука, 1981.
Бжихатлов Х.Г., Карасев И.М., Лесковский И.П., Нахушев А.М. Избранные вопросы дифференциальных и интегральных уравнений. Нальчик. 1972.
Wolfersdorf L. Mfth. Zeitschr., 90,1,1965.
Езаова А.Г. Краевая задача для одного уравнения третьего порядка с кратными характеристиками.// Нальчик, вестник КБГУ, серия «математические науки». Вып. 3, 2003.
Мусхелишвили Н.И. Сингулярные интегральные уравнения. М., Наука, 1968.
Джураев Т.Д. Краевые задачи для уравнений смешанного и смешанно- составного типов. Ташкент, Фан, 1979.
Kattabriga L. Un problem al kontrono per ulna education did or dine despair // Anal Della scholar normal did pisafisa mat. 1959. №2.
|