Курсовая работа: Синтез системи підпорядкованого регулювання швидкості
|
Название: Синтез системи підпорядкованого регулювання швидкості Раздел: Рефераты по транспорту Тип: курсовая работа | |||||||||
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД ДОНЕЦЬКИЙ НАЦIОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ Кафедра «ЕАПУ» ПОЯСНЮВАЛЬНА ЗАПИСКА до курсового проекту з дисципліни «Теорія автоматичного керування» на тему: «Синтез системи підпорядкованого регулювання швидкості»
Пояснювальна записка містить: 40 сторінок, 27 рисунків, 3 джерела. Об’єктом розробки є двоконтурна система підпорядкованого регулювання швидкості двигуна постійного струму з номінальними даними: напругою 220 В, струмом 50 А. Розроблена система повинна мати такі показники: час розгону 0,8 с, перерегулювання роботи контуру швидкості 25 %. Метою роботи є систематизація знань з курсу дисципліни “Теорія Автоматичного Керування”, та отримання практичних навичок у розв’язанні поставлених завдань, шляхом розробки двоконтурної системи регулювання швидкості двигуна, а також підготовка до курсів з інших дисциплін та дипломного проектування. СИНТЕЗ, АНАЛІЗ, ЗВОРОТНИЙ ЗВ’ЯЗОК, СТАЛА ЧАСУ, МОДУЛЬНИЙ ОПТИМУМ, ЗАДАВАЧ ІНТЕНСИВНОСТІ, СТРУКТУРНА СХЕМА, ОПЕРАЦІЙНИЙ ПІДСИЛЮВАЧ, СИСТЕМА ПІДПОРЯДКОВАНОГО РЕГУЛЮВАННЯ ПЕРЕЛІК ПОЗНАЧЕНЬ І СКОРОЧЕНЬ ВП – вентильний перетворювач; ДН – давач напруги; ДС – давач струму; ЕРС – електрорушійна сила; ЗІ – задавач інтенсивності; ІППН – імпульсний перетворювач постійної напруги; КРС – контур регулювання струму; КРШ – контур регулювання швидкості; ЛАЧХ – логарифмічна амплітудна частотна характеристика; ЛО – ланка обмеження; ЛФЧХ – логарифмічна фазова частотна характеристика; МО – модульний оптимум; РС – регулятор струму; РШ – регулятор швидкості; СПР – система підпорядкованого регулювання; hC (t) – перехідна функція контуру регулювання струму; hш (t) – перехідна функція контуру регулювання швидкості; I – струм якоря; Ki – коефіцієнт зворотного зв’язку за струмом; Kк.с (р) – передавальна функція замкненого контуру регулювання струму; Kк.ш (р) – передавальна функція замкненого контуру регулювання швидкості; Kш – коефіцієнт зворотного зв’язку за швидкістю; Rя – опір силового кола вентильний перетворювач–двигун; tc – час першого досягання перехідним процесом усталеного значення; Тi – стала часу інтегрування розімкненого контуру регулювання струму; Тμ – мала некомпенсована стала часу контуру регулювання струму; Тω – вентильний перетворювач; ТМ – електромеханічна стала часу приводу; ТС – стала часу інтегрування розімкненого контуру регулювання швидкості; Тя – електромагнітна стала часу кола вентильний перетворювач–двигун; tм – час досягання перехідним процесом максимального значення; Uз.ω – напруга, пропорційна заданій швидкості двигуна; Uз.с – напруга, пропорційна заданому струму двигуна; UЗІ – вихідна напруга задавача інтенсивності; Wp.c (р) – передавальна функція регулятора струму; Wp.ш (р) – передавальна функція регулятора швидкості; Wк.с (р) – передавальна функція розімкненого контуру регулювання струму; Wк.ш (р) – передавальна функція розімкненого контуру регулювання швидкості; δ – перерегулювання; ΔωС – статичне падіння швидкості; ε – прискорення електроприводу; ω – швидкість двигуна; Мр – резонансний максимум амплітудно–частотної характеристики замкненої системи; с – конструктивна стала двигуна. ВСТУП В процесі реалізації розповсюдження та використання, значного розвитку та розповсюдження отримали електроприводи постійного струму. Це обумовлено можливістю реалізації підпорядкованої системи регулювання швидкості (яка була розглянута в даному курсовому проекті) з використанням універсальних блочних систем регулювання. Сучасний етап розвитку техніки керування електроприводами постійного струму характеризуються випуском комплектних електроприводів. Основні позитивні сторони таких систем – це можливість реалізації високих динамічних характеристик електроприводів, простота їх налагодження і експлуатації, а також можливість широкої уніфікації схем і конструкцій елементів, в тому числі пристроїв, призначених не тільки для автоматизації електроприводів, але й для розв’язання задач автоматизації технологічних процесів. 1. МАТЕМАТИЧНИЙ ОПИС ЕЛЕМЕНТІВ САК І СКЛАДАННЯ СТРУКТУРНОЇ СХЕМИ 1.1 Двигун постійного струму незалежного збудження Для математичного опису САК, доцільно розбити її на кілька однорідних за властивостями та функціональним призначенням елементів. Вхідний сигнал повинний впливати на вихідний сигнал, але вихідний сигнал не повинний впливати на вхідний сигнал. Математичний опис заснований на тотожності диференціальних рівнянь, що описують процеси в оригіналі і функціональних залежностях між вхідними і вихідними величинами, представлений у перетворенні Лапласа. У систему підпорядкованого регулювання входять: – задавач інтенсивності (ЗІ); – регулятор швидкості (РШ); – регулятор струму (РС); – датчик швидкості (ДШ); – датчик струму (ДС); – двигун (Д). Спрощена схема двигуна постійного струму і схема заміщення системи “перетворювач–двигун” представлена на рис. 1.1.
Рисунок 1.1 – Спрощена схема двигуна постійного струму і схема заміщення системи “перетворювач–двигун” Двигун постійного струму описується наступною системою рівнянь:
де: Rя =Rп +Rд – активний опір якірного ланцюга двигуна; Lя =Lп +Lд – індуктивність якірного ланцюга двигуна; Еп =U – ЕРС перетворювача; Ед – ЕРС двигуна;
Приймаючи потік Ф=const, можна позначити k∙Ф=с, тоді:
М – обертаючий момент двигуна
МС – статичний момент двигуна
У підсумку одержуємо наступну систему рівнянь:
Застосувавши перетворення Лапласа і виконавши підстановку:
де: Тя =Lя/Rя – електромагнітна постійна часу якоря; Тм - електромеханічна постійна часу двигуна. Запишемо отриману систему рівнянь наступним чином:
Рисунок 1.2 – Структурнасхема двигуна Згідно (1.8) Складаємо структурну схему двигуна постійного струму (рис. 1.2). 1.2 Вентильний перетворювач Вентильний перетворювач – пристрій, створений на базі вентильних елементів що перетворює змінний струм в постійний з можливістю регулювання рівня напруги, і найчастіше являє собою повністю керований випрямлював напруги. З точки зору своїх властивостей вентильний перетворювач являє собою нелінійну дискретну ланку, проте в безперервних системах не лінійністю та дискретністю можна знехтувати. В такому разі ВП має властивості ланки запізнювання f(t-Tu) → F(p)ּe-pTu≈ F(p)/(1+ pTu). F(p) являє собою пропорційну ланку, що видно з того, що ВП керується сигналами малої потужності, а на виході отримують потужність необхідну для роботи електроприводу. Запишемо ПФ ланки вентильного перетворювача:
де Eп – ЕРС вентильного перетворювача; Uk – напруга керування; kВП – коефіцієнт передачі вентильного перетворювача; Tμ – сума всіх малих постійних часу контуру струму. 1.3 Давач струму
Рисунок 1.3 – Схема давача струму Давач струму дозволяє здійснити зворотний зв'язок по струму і являє собою шунт, включений у силовий ланцюг “вентильний перетворювач – двигун” і підключений до нього датчика струму. Структурна схема давача струму приведена на рис 1.6. Шунт вибирають таким, щоб він пропускав гранично припустимий чи максимально припустимий струм двигуна. ДС – давач струму, здійснює потенційну розв'язку вхідного і вихідного сигналу.
З (1.10) знаходимо 1.4 Давач швидкості Давач швидкості служить для одержання інформації про швидкість двигуна та передачі сигналу про неї у вигляді напруги для формування зворотнього зв’язку за швидкістю. Це спеціалізована машина постійного струму невеликої потужності зі збудженням від постійного магніту (тахогенератор), вихідна напруга якого пропорційна швидкості:
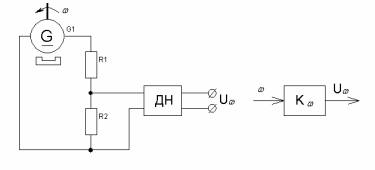
де γ – коефіцієнт пропорційності. Основна вимога – наближення зазначеної залежності до лінійної, що визначає точність його роботи. Вузол давача швидкості і його структурна схема приведені на рисунку 1.4.
Рисунок 1.4 – Вузол давача швидкості ДН – давач напруги, здійснює потенційну розв'язку вхідного і вихідного сигналу. Коефіцієнт передачі датчика:
1.5 Задавач інтенсивності Задавач інтенсивності встановлений на вході контуру регулювання швидкості (КРС). Він формує сигнал, пропорційний бажаній зміні напруги в процесі розгону і гальмування електропривода.
Графік, що пояснює роботу задавача інтенсивності, представлений на рисунку 1.5, а структурна схема ЗІ приведена на рис 1.6.
Рисунок 1.5 – Залежність UЗІ (t)
Рисунок 1.6 – Структурна схема ЗІ На структурній схемі ЛО – ланка обмеження. Уся система підпорядкованого регулювання приведена на рис 1.7.
Рис. 1.7 2. КОНТУР РЕГУЛЮВАННЯ СТРУМУ ЯКОРЯ 2.1 Синтез регулятора струму Структурна схема контура регулювання струму зображена на рисунку 2.1
Рисунок 2.1 – Структурна схема КРС Як видно із структурної схеми КРС, в ньому є одна велика стала часу Тя і малі сталі часу вентильного перетворювача Тп і давача струму Тд.с , розташовані в прямому каналі та каналі зворотного зв’язку. Визначаємо коефіцієнт передачі по струму:
Згідно з принципом компенсації великих сталих часу, для формування одноразово інтегрувального КРС передавальна функція РС повинна мати вигляд:
де Ті – стала часу інтегрування розімкненого КРС, яку необхідно визначити. Для того, щоб врахувати інерційність РС, його передавальну функцію слід записати у такому вигляді:
де ТФ – стала часу, що характеризує інерційність регулятора струму. Згідно з цим передавальна функція розімкненого КРС матиме вигляд:
Згідно з цим передавальна функція замкненого КРС матиме вигляд:
2.2 Аналіз динаміки КРС 2.2.1 Аналіз динаміки КРС без врахування впливу проти–ЕРС Замінимо всі інерційності КРС однією, зосередженою в ВП. Вкажемо отриману структурну схему на рис. 2.2.
Рисунок 2.2. – Структурна схема КРС Передавальні функції оптимізованих розімкненого і замкненого контурів регулювання струму мають вигляд:
Згідно з модульним оптимумом, знаходимо сталу інтегрування:
ЛАЧХ та ЛФЧХ розімкненого контуру КРС зображена на рис. 2.5 та рис. 2.7. Частота спряження:
Частота зрізу:
Виведемо перехідну функцію оптимізованого КРС:
Остаточно перехідна функція оптимізованого КРС має вигляд:
Перехідна функція замкненого контуру КРС зображена на рис. 2.2. · час першого узгодження:
· час досягнення максимуму:
Таким чином, КРС настроєно на оптимальні параметри функціонування. 2.2.2 Розрахунок динаміки КРС з врахуванням впливу проти–ЕРС Синтез контуру регулювання струму у попередньому пунктібуло проведено без урахування внутрішньої ЕРС двигуна. Для зручності аналізу при наявності внутрішньої ЕРС скористуємось наступними перетвореннями структурної схеми двигуна (рис. 2.3).
Рисунок 2.3 – Послідовність перетворювань структурної схеми двигуна з урахуванням внутрішньої ЕРС Структурна схема КРС з врахуванням впливу проти–ЕРС після перетворення дістане вигляд, представлений на рис. 2.4. ЛАЧХ та ЛФЧХ розімкненого контуру КРС зображена на рис. 2.5 та рис. 2.7. Перехідна функція замкненого контуру КРС зображена на рис. 2.6.
Рисунок 2.4. – Структурна схема КРС з врахуванням впливу проти–ЕРС Передавальна функція розімкненого КРС за керуючою дією:
Передавальна функція замкненого КРС за керуючою дією:
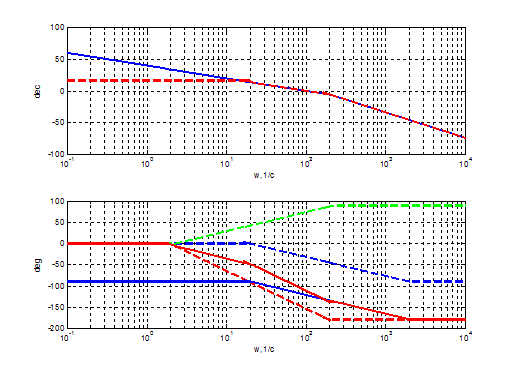
Рисунок 2.5 – ЛАЧХ і ЛФЧХ розімкненого контуру регулювання струму: 1 − характеристики без врахування впливу проти−ЕРС; 2 − характеристики з врахуванням впливу проти−ЕРС
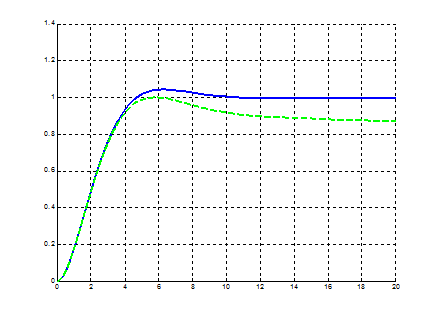
Рисунок 2.6 − Перехідні функції замкненого контуру регулювання струму: 1 − характеристики без врахування впливу проти−ЕРС; 2 − характеристики з врахуванням впливу проти−ЕРС
Рисунок 2.7 – Асимптотичні ЛАЧХ і ЛФЧХ розімкненого контуру регулювання струму: 1 − характеристики без врахування впливу проти−ЕРС; 2 − характеристики з врахуванням впливу проти−ЕРС Функція h(t) (2) характеризується такими показниками якості: · час першого узгодження:
З аналізу впливу проти-ЕРС можна визначити, що без компенсації проти-ЕРС система має гірші динамічні та статичні властивості, а саме більшій показники перегулювання та менше устелене значення вихідної величини хоча й менший час першого узгодження. Передавальна функція КРС за збуренням:
Згідно з принципом суперпозиції: струм якорю є сумою реакцій КРС на керуючий сигнал
Усталене значення струму якоря:
Тобто усталене значення струму якоря в 1,5 рази перевищує номінальний струм якоря, тому потрібно застосовувати компенсацію впливу проти−ЕРС. З формули (2.21) видно, що перехідні процеси так і усталене значення струму при врахуванні зворотнього зв`язку за ЕРС двигуна, залежать не тільки від впливу по каналу завдання, але й від навантаження. Крім цього КРС стає статичним відносно керуючої дії, оскільки інтегральна компонента регулятора струму компенсується диференційною складовою двигуна. 2.2.3 Методи компенсації впливу проти−ЕРС Для компенсації впливу проти−ЕРС можна застосувати регулятор струму з передавальною функцією:
яка забезпечить оптимізацію контуру регулювання струму за модульним оптимумом, бо повністю компенсує інерційність двигуна та усуває вплив диференцуючої дії двигуна на статичні властивості КРС. Недоліком цього способу компенсації впливу проти−ЕРС є складність в реалізації регулятора струму та налагодження системи. Найбільш універсальним рішенням, яке забезпечує компенсацію впливу проти−ЕРС на характер перехідних процесів у всіх режимах є використання додатного зворотного зв’язку за ЕРС двигуна, що подається на вхід вентильного перетворювача або регулятора струму. Слід також додати, що реалізація безінерційного сигналу ЕРС двигуна пов’язана з певними труднощами – використання серійних давачів ЕРС для компенсації її впливу на динаміку приводу супроводжується при великій інерційності якірного кола двигуна незадовільними динамічними режимами, а використання тахогенератора для одержання пропорційного для ЕРС сигналу є неприйнятним при двузонному регулюванні швидкості. 2.2.4 Реалізація регулятора струму на операційних підсилювачах Регулятор струму, який має передавальну функцію (2.1) можна реалізувати за схемою:
Рисунок 2.8 – Реалізація регулятора струму Приймаємо RC.3 =R3.C , тоді передавальна функція РС по обох каналах завдання та зворотного зв’язку буде мати вигляд:
де
Із рівнянь 2.2, 2.24 та 2.25 одержуємо такі умови для вибору параметрів:
Задамося значенням C3.3 =2 мкФ=2ּ10−6 Ф, та знаходимо інші параметри:
3. КОНТУР РЕГУЛЮВАННЯ ШВИДКОСТІ 3.1 Синтез регулятора швидкості Структурна схема контуру регулювання швидкості має вигляд:
Рисунок 3.1 – Структурна схема КРШ Коефіцієнт передачі датчика швидкості визначається по формулі:
де Для реалізації дворазово інтегрувальної системи необхідний ще один інтегратор в РШ (один вже є в об'єкті регулювання). Передавальна функція РШ:
де Тш – стала інтегрування розімкненого КРШ, яку необхідно визначити. Враховуючи це контур регулювання швидкості буде мати вигляд, який представлено на рисунку 3.2.
Рисунок 3.2 – Розрахункова схема контура регулювання швидкості з інтегральним регулятором Тоді передавальна функція розімкненого КРШ буде мати вигляд:
Передавальна функція мала вигляд:
Тоді передавальна функція розімкненого КРШ буде мати вигляд:
3.2 Аналіз динаміки контура регулювання швидкості 3.2.1 Аналіз динаміки контура регулювання швидкості з безінерційним зворотним зв’язком за швидкістю (Тω =0) Оскільки Тw =0, то передавальна функція розімкненого КРШ за керуючою дією має вигляд:
Передавальна функція замкненого КРШ за керуючою дією має вигляд:
Визначимо параметри Т1 і Тш методом резонансного максимуму Резонансний максимум при даному перерегулюванні:
Розрахунок параметрів ПІ–РШ при Tω =0. Сума сталих часу, відповідних “правим” частотам спряження:
Розраховуємо частоту зрізуw с (рис. 1.18 [1]):
Розрахуємо S w л (рис. 1.18 [1]):
ЛАЧХ та ЛФЧХ розімкненого контуру КРШ зображена на рис. 3.6 та рис. 3.8, Перехідна функція замкненого контуру КРШ зображена на рис. 3.7. 3.2.2 Аналіз динаміки контура регулювання швидкості з інерційним зворотним зв’язком за швидкістю (Тω≠0) Розрахунок параметрів ПІ–РШ при Tω ≠0. Контур регулювання швидкості буде мати вигляд, який представлено на рисунку 3.3.
Рисунок 3.3 – Розрахункова схема контура регулювання швидкості з ПІ регулятором та з інерційним зворотнім зв’язком за швидкістю Передавальна функція розімкненого КРШ за керуючою дією має вигляд:
Передавальна функція замкненого КРШ за керуючою дією має вигляд:
Стала часу інерційності КРШ:
Сума сталих часу, відповідних “правим” частотам спряження:
Далі повторюємо розрахунок згідно (3.8) – (3.11). Розраховуємо частоту зрізу wс :
Розраховуємо Swл =w1 :
ЛАЧХ таЛФЧХрозімкненого контуруКРШзображена на рис. 3.4. Перехідна функція замкненого контуру КРШ зображена на рис. 3.5.
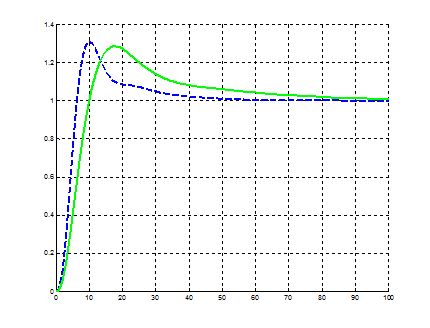
Рисунок 3.4 – ЛАЧХ і ЛФЧХ розімкненого контуру регулювання швидкості: 1 – з безінерційним зворотнім зв’язком; 2 – з інерційним зворотнім зв’язком
Рисунок 3.5 – Перехідні функції замкненого контуру регулювання швидкості: 1 – з безінерційним зворотнім зв’язком; 2 – з інерційним зворотнім зв’язком З аналізу впливу інерційності зворотного зв’язку можна визначити, що з інерційним зворотним зв’язком система має гірші динамічні властивості, а саме значно більший показник часу першого узгодження та також час перехідного процесу значно більший, хоча й дещо менше перегулювання. Інерційний зв’язок на статичні властивості системи не впливає. Вибираємо уставку обмеження вихідної напруги регулятора швидкості Uoрш зумовиобмеження стопорного струму нерухомого двигуна:
3.2.3 Реалізація регулятора швидкості на операційних підсилювачах Передавальна функція регулятора швидкості має вигляд
де Схема за якою можливо реалізувати КРШ зображена на рисунку 3.6.
Рисунок 3.6 – Реалізація КРШ на операційних підсилювачах Для цієї схеми: Т1 = Rз.з ·Cз.з
Передавальна функція по обох каналах (завдання та зворотнього зв`язку за струмом) буде мати вид:
З отриманих вище формул отримуємо наступні умови для вибору параметрів РШ:
Звідки (попередньо обравши Сз.з = 5 мкФ):
4. СИНТЕЗ ТА РЕАЛІЗАЦІЯ ЗАДАВАЧА ІНТЕНСИВНОСТІ Задавач інтенсивності можна реалізувати за такою схемою:
Рисунок 4.1 – Схема задавача інтенсивності Задавач інтенсивності (ЗІ) – це пристрій, що перетворює ступінчастий вхідний вплив в лінійно змінний сигнал с потрібним значенням похідної. ЗІ застосовується у системах керування електроприводами для забезпечення необхідного темпу розгону (гальмування) та вибору початкового зазору механізмів, з уникненням удару. Операційний підсилювач А1 виконує функцію компаратора, зрівнюючого вхідну напругу Uвх з інверсною вихідною напругою ЗИ. В залежності від співвідношення цих напруг U1 може приймати три значення +Uмакс, 0, -Uмакс. При розімкнутому зворотному зв’язку А1, значення напруги ±U1макс близькі до напруги живлення. Для більшої стабільності вихідної напруги U1 в зворотний зв’язок А1 включають великий опірR6. Операційний підсилювач А2 виконує функцію інтегратора, вихідна напруга, якого змінюється в часі по закону:
Добуток
Операційний підсилювач А3 працює у режимі інвертора вихідної напруги для формування негативного зворотнього зв’язку на компаратор. Визначимо Тзі з умови що прискорення (гальмування) приводу здійснюється з динамічним струмом, який дорівнює 0,8÷1,5ּІном. Розрахунок будемо вести у відносних одиницях: Потрібний час розгону у відносних одиницях:
Струм короткого замикання у відносних одиницях:
Потрібний темп прискорення приводу у відносних одиницях:
Закон наростання (спадання) напруги при розгоні (гальмуванні) електроприводу:
де Тзі – стала інтегрування задавача інтенсивності. Приймаємо U0 =5 B. Знайдемо сталу ТЗІ . При uзі
(tр)=
Приймаємо С=100 мкФ. Тоді
Визначимопохибку швидкостіпри заданому темпі прискоренняeр для Тw =0. Згідно до рисунка 3.5 знаходимо:
Знаходимо усталене значення похибки:
Визначимошвидкіснупохибкупри заданому темпі прискорення eр для Тw ¹0.
Знаходимо усталене значення похибки:
5. АНАЛІЗ ДИНАМІКИ САК ПРИ РОБОТІ ВІД ЗАДАВАЧА ІНТЕНСИВНОСТІ Графіки перехідних процесів i(t), w(t), Uзі(t) при роботі привода від задавача інтенсивності при різних режимах:
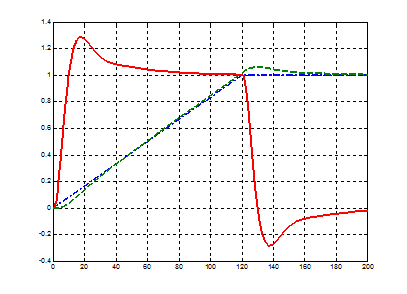
Рисунок 5.1 – Перехідні процеси у СПР при Tω =0, іс=0
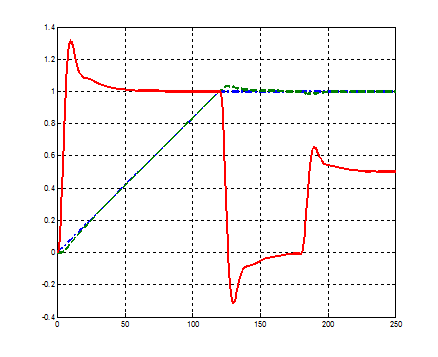
Рисунок 5.2 – Перехідні процеси у СПР при Tω ≠0, іс=0
Рисунок 5.3 – Перехідні процеси у СПР при Tω =0, іс=іном При роботі привода від ЗІ останній формує сигнал завдання Uзw(t), який відповідає потрібному закону зміни швидкості wз(t). Замкнений КРШ здійснює відпрацювання цього закону і визначає динамічні і статичні властивості системи при роботі РШ на лінійній характеристиці. Вихідна напруга РШ обмежується на рівні, пропорційному заданому значенню струму в стопорному режимі. ВИСНОВОК В процесі виконання цієї курсової роботи була синтезована двоконтурна система підпорядкованого регулювання електроприводом постійного струму. КРС був синтезован по МО, а контур регулювання швидкості – по мінімуму резонансного максимуму. У якості РС та РШ служить ПІ–регулятор. Система працює від ЗІ. Була оцінена динаміка КРС і КРШ, а також усієї САК при роботі від ЗІ. Була виконана реалізація РС та РШ, а також ЗІ на операційних підсилювачах. Було спроектовано контур регулювання струму та підібрана стала часу контура. Також, було спроектовано контур регулювання швидкості. Враховуючи параметри завдання було розроблено регулятор швидкості і реалізовано його на операійних підсилювачах.. Було досліджено вплив інерційного зворотнього зв`язку на перехідні параметри контура регулювання швидкості. Для реалізації однакового темпу розгону та сповільнення двигуна на вхід контура регулювання швидкості було встановлено задавач інтесивності, який формує сигнал трапецієдальної форми. Також було разроховано сталу часу задавача інтенсивності і спроектовано схему його реалізації на операційних підсилювачах. Також були побудовані перехідні процеси i(t), w(t), Usi (t) при різних значенях Тw та Іс . ПЕРЕЛІК ПОСИЛАНЬ1. Коцегуб П.Х. “Синтез вентильних приводів постійного струму”. ДонНТУ, 2000. 2. Бесекерский В.А., Попов Е.П. “Теория систем автоматического регулирования”. – Москва, Наука, 1975. 3. Коцегуб П.Х, Толочко О.І. “Оптимизация систем управления с задатчиком интенсивности”. – электротехническая промышленность. Серия “Электропривод”, 1976. |
|||||||||

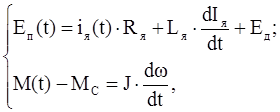 (1.1)
(1.1) (1.6)
(1.6) (1.7)
(1.7) (1.8)
(1.8) 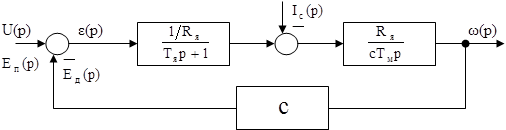
 , (1.9)
, (1.9)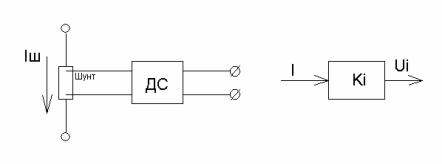
 , (1.12)
, (1.12)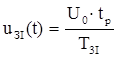 . (1.13)
. (1.13)


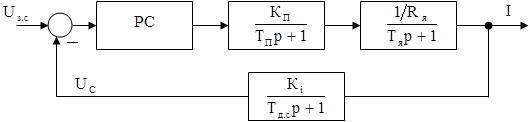
 ; (2.1)
; (2.1) .
. , (2.2)
, (2.2)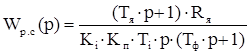 , (2.3)
, (2.3)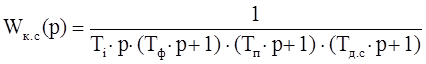 . (2.4)
. (2.4)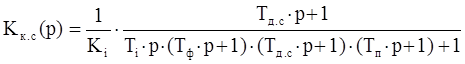 . (2.5)
. (2.5)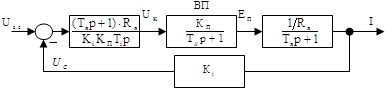
 ; (2.6)
; (2.6)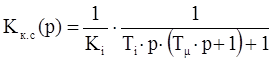 .
. ,
,  ,
,  (2.11)
(2.11) (2.12)
(2.12)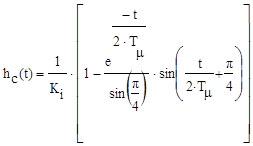 . (2.14)
. (2.14)

 (2.17)
(2.17)
 (2.19)
(2.19)  , (2.21)
, (2.21) 


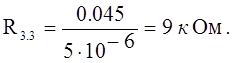 (2.30)
(2.30)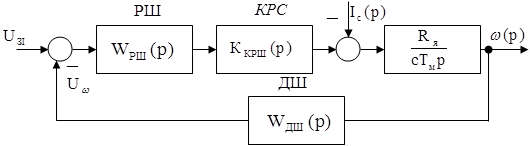
 ,
, 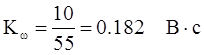 (3.1)
(3.1) – кутова швидкість двигуна.
– кутова швидкість двигуна. (3.2)
(3.2) 
 . (3.3)
. (3.3)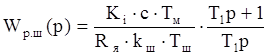 . (3.4)
. (3.4) (3.5)
(3.5)
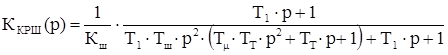 (3.6)
(3.6)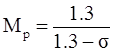 ,
, 
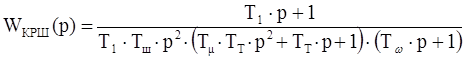 (3.11)
(3.11)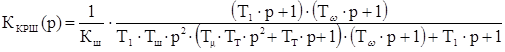 (3.12)
(3.12)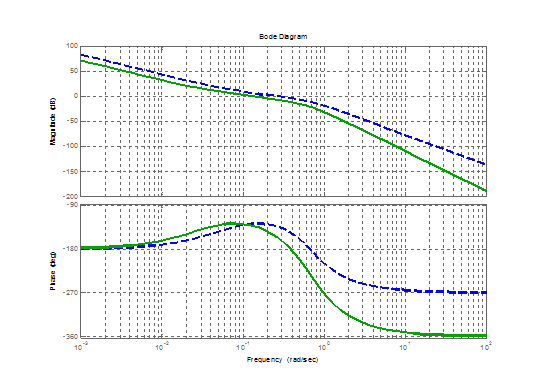
 . (3.16)
. (3.16)
 (3.17)
(3.17) , (3.18)
, (3.18)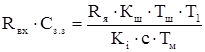 (3.19)
(3.19)
 (4.1)
(4.1) (4.3)
(4.3)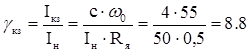 (4.4)
(4.4) (4.5)
(4.5)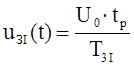 ,
,
 с (4.6)
с (4.6) (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10)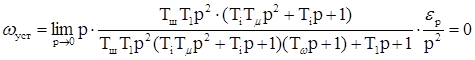 (4.11)
(4.11)