Министерство образования и науки Украины
Открытый международный университет развития человека “Украина"
Горловский филиал
Кафедра физической реабилитации
РЕФЕРАТ
по дисциплине:
Методы исследований в физической культуре и спорте,
физической реабилитации
ТЕМА:
”Корреляция и непараметрические критерии различия в педагогических исследованиях "
Выполнил:
студент 2-го курса группы ФР-06
дневного отделения
факультета “Физическая реабилитация"
Орёл Олег Альбертович
2008
План
Корреляция
Непараметрические критерии различия
Список литературы
В любом педагогическом процессе составляющие его факторы находятся в тесной взаимосвязи. Умение изменить один фактор так, чтобы получить соответствующее изменение другого, сделает педагогический процесс более целенаправленным. В науке различают две формы взаимосвязи.
Функциональная связь
отражает четкую однозначную зависимость, при которой изменение какого-либо одного фактора неизбежно приводит к однозначному изменению другого. Подобные связи характерны для "точных" наук. В педагогике они, если и наблюдаются, то в самых общих вариантах и в пределах каких-то условных границ. Установление функциональных связей между педагогическими факторами - дело интересное, но чрезвычайно проблематичное.
Более реальным является установление так называемых статистических связей,
или корреляций.
Корреляция позволяет находить статистически достоверные количественные меры связи в тех случаях, когда какому-либо одному фактору соответствует не одно, а несколько значений какого-либо другого фактора, причем варьирующих в каких-то пределах. Связь в этом случае будет выражаться в средних значениях, полученных на целом ряде изменений.
Практическая значимость определения величины и характера корреляции заключается в том, что с ее помощью можно установить функциональное сходство или различие между физическими упражнениями, например общеподготовительными и соревновательными. Однако, применяя корреляцию, следует помнить, что, во-первых, наличие статистической связи отнюдь не означает автоматического выявления и причинных связей, поэтому использовать корреляционный анализ для понимания причинных факторов надо осторожно; во-вторых, нельзя механически применять корреляцию там, где по природе своей педагогические факторы не обладают зависимостью.
Коррелирующие факторы подразделяются на причинные
, т.е. те, которые видоизменяются первыми, вызывают изменения других факторов, и следственные,
т.е. те, которые видоизменяются под влиянием причинных факторов. Причем следственные факторы могут принимать ряд значений в определенных границах. Различают корреляции нескольких направлений:
прямая положительная корреляция, при которой увеличение причинного фактора вызывает увеличение следственного фактора; например, увеличение силы мышц-разгибателей ног положительно сказывается на росте результатов в прыжках в высоту с разбега (В.М. Дьячков, Г.И. Черняев, 1965).
прямая отрицательная корреляция, при которой уменьшение причинного фактора вызывает уменьшение следственного фактора; например, уменьшение нагрузки приводит к понижению частоты сердечных сокращений;
обратная положительная корреляция при которой уменьшение причинного фактора вызывает увеличение следственного фактора; например, уменьшение длины дистанции приводит к увеличению скорости бега;
обратная отрицательная корреляция, при которой увеличение причинного фактора вызывает уменьшение следственного фактора; например, увеличение силы мышц под влиянием занятий тяжелой атлетикой может привести к ухудшению результатов в беге на длинные дистанции (М.И. Майсурадзе, 1962).
Математическое значение корреляции выражается ее коэффициентом от - 1 (максимальной отрицательной связи) до +1 (максимальной положительной связи) десятичными дробями с точностью до второго знака после запятой.
Количественную меру связи принято различать по нескольким уровням:
слабая связь - при коэффициенте корреляции до 0,30,средняя связь - при коэффициенте корреляции от 0,31 до 0,69,сильная связь - при коэффициенте корреляции от 0,70 до 0,99.
Коэффициент корреляции равный 1 свидетельствует о наличии функциональной связи. Если изменение одного фактора не влияет на величину другого, то связь отсутствует, т.е. данные факторы между собой нейтральны.
Ранговая корреляция Спирмена (корреляция рангов) является одним из наиболее простых способов установления меры связи между факторами. Само название метода указывает на то, что связь определяется между рангами, т.е. рядами полученных количественных значений, ранжированных в убывающем или возрастающем порядке. Следует иметь в виду, что, во-первых, ранговую корреляцию не рекомендуется проводить, если связанных пар меньше четырех и больше двадцати; во-вторых, ранговая корреляция позволяет устанавливать связь и в том случае, если значения носят, так сказать, полуколичественный характер, т.е., не имея числовых выражений, отражают четкий порядок следования этих величин; в-третьих, ранговую корреляцию целесообразно применять в тех случаях, когда достаточно получить лишь приблизительную информацию.
Чтобы рассчитать коэффициент ранговой корреляции, необходимо:
расположить количественные значения причинного фактора в убывающем (возрастающем) порядке; например, для установления влияния уровня физической работоспособности лыжников (причинный фактор), выявленного при помощи дозированной нагрузки на велоэргометре, на результат в гонке на 15 км (следственный фактор) уровень физической работоспособности ранжировался (Г.И. Мызан, 1974) в убывающем порядке (колонка "А");
параллельно первому ряду записать соответствующие значения следственного фактора, в данном случае - результат в гонке на 15 км (колонка "Б"); порядок значений этого фактора будет подчинен порядку значений причинного фактора, а поэтому может не подчиняться принципу возрастания или убывания;
| ФР170
, кГм/мин/кг |
Результат гонки, мин |
Ранги |
Разность рангов |
Квадрат разности рангов |
| ФР170
|
результат |
| А |
Б |
а |
б |
d =
а - б |
d 2
|
| 24,8 |
63 |
1 |
2 |
-1 |
1 |
| 24,2 |
61 |
2 |
1 |
+1 |
1 |
| 24,0 |
72 |
3 |
5 |
-2 |
4 |
| 20,4 |
71 |
4 |
4 |
0 |
0 |
| 20,1 |
70 |
5 |
3 |
+2 |
4 |
| 19,0 |
82 |
6 |
10 |
-4 |
16 |
| 17,5 |
77 |
7 |
7 |
0 |
0 |
| 17,2 |
75 |
8 |
6 |
+2 |
4 |
| 16,8 |
79 |
9 |
8 |
+1 |
1 |
| 16,3 |
81 |
10 |
9 |
+1 |
1 |
| n
= 10 |
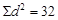 |
обозначить цифрами порядковые места значений причинного фактора (колонка "а"); естественно, что раззначения этого фактора расположены в убывающем порядке, то цифры порядковых мест будут расположены в возрастающем порядке; если количественные показатели того или иного фактора оказываются одинаковыми, то их порядковые места обозначаются тем числом, которое составляет среднюю арифметическую величину их порядковых мест;
обозначить цифрами порядковые места значений следственного фактора (колонка "б");
подсчитать число коррелируемых парных значений (n
); в данном примере их 10;
вычислить разность рангов (d = а
- б) с сохранением соответствующего знака; в данном примере: 1 - 2 = - 1 и т.д.;
вычислить квадрат разности рангов (d2
);
в данном примере: - 12
= 1 и т.д.;
вычислить сумму квадратов разности рангов (Sd2
); в данном примере она равна 32;
вычислить коэффициент корреляции рангов ρ по формуле:
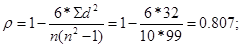
произвести оценку вычисленного коэффициента, т.е. установить, во-первых, существует ли статистически достоверное различие между полученным значением коэффициента и нулем; во-вторых, проявятся ли выявленные связи (или их отсутствие), если коэффициент корреляции будет рассчитываться по тем же самым признакам, но на других группах исследуемых или на тех же самых группах, но в других условиях; значимость коэффициента корреляции рангов определяется двумя путями:
а) путем сравнения с принятыми уровнями меры количественной связи; в данном примере величина коэффициента корреляции, равная 0,807, говорит о сильной мере количественной связи;
Критические значения коэффициентов корреляции рангов Спирмена (ρ)
Число
коррелируемых
пар, n
|
Уровень
значимости, P
|
| 0,05 |
0,01 |
| 4 |
1,000 |
- |
| 5 |
0,900 |
1,000 |
| 6 |
0,329 |
0,943 |
| 7 |
0,714 |
0,893 |
| 8 |
0,643 |
0,833 |
| 9 |
0,600 |
0,783 |
| 10 |
0,564 |
0,746 |
| 12 |
0,506 |
0,712 |
| 14 |
0,456 |
0,645 |
| 16 |
0,452 |
0,601 |
| 18 |
0,399 |
0,564 |
| 20 |
0,377 |
0,534 |
| 22 |
0,359 |
0,508 |
| 24 |
0,343 |
0,485 |
| 26 |
0,329 |
0,465 |
| 28 |
0,317 |
0,448 |
| 30 |
0,306 |
0,432 |
б) по таблице достоверности коэффициента корреляции; определенный коэффициент, равный 0,807, может быть признан значимым в том случае, если его величина будет превышать табличное значение для 10 парных наблюдений; по таблице для 10 пар уровень значимости (Р) равен
0,564 или 0,746, следовательно: 0,564<0,807>0,746 т.е. коэффициент превышает Р
- = 0,01 и может считаться значимым с вероятностью ошибки менее 0,01.
сделать методический вывод, т.е. выяснить внутренний высчитанного коэффициента корреляции; в приведенном примере можно убежденно говорить, что среди прочих условий на результат в лыжной гонке оказывает влияние уровень физической работоспособности спортсмена.
Коэффициент корреляции r
обладает более высокой степенью точности количественной характеристики связи между факторами.
Расчет коэффициента r
производится по формуле:
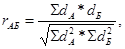
где А и Б - коррелируемые ряды вариант dА
и dБ
-
отклонения вариант от средних значений этих рядов (разность между каждым значением варианты ряда и средней арифметической величиной данного ряда). Точность вычисления по формуле должна быть достаточно высокой, не менее двух знаков после запятой.
Последовательность вычисления коэффициента r
показана на примере результатов исследования, использованных для демонстрации расчета коэффициента ранговой корреляции.
Составить таблицу для первичных числовых операций, для чего в первых двух колонках расположить показатели уровня физической работоспособности (ФР170
) и показатели спортивного результата в гонке на 15 км; ранжирование показателей не обязательно.
| ФР170
, кГм/мин/кг |
Результат гонки, мин |
d
А
|
d
Б
|
d
Б
2
|
d
А
2
|
d
А
d
Б
|
| А |
Б |
| 24,8 |
63 |
+4,8 |
-10 |
23,04 |
100 |
-48,0 |
| 20,1 |
70 |
+0,1 |
-3 |
0,01 |
9 |
-0,3 |
| 20,4 |
71 |
+0,4 |
-2 |
0,16 |
4 |
-0,8 |
| 24,0 |
72 |
+4,0 |
-1 |
16,00 |
1 |
-4,0 |
| 17,5 |
77 |
-2,5 |
+4 |
6,25 |
16 |
-10,0 |
| 16,8 |
79 |
-3,2 |
+6 |
10,24 |
36 |
-19,2 |
| 19,0 |
82 |
-1,0 |
+9 |
1,00 |
81 |
-9,0 |
| 17,2 |
75 |
-2,8 |
+2 |
7,84 |
4 |
-5,6 |
| 24,2 |
61 |
+4,2 |
-12 |
17,64 |
144 |
-48,4 |
| 16,3 |
81 |
-3,7 |
+8 |
16,69 |
64 |
-29,6 |
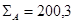 |
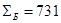 |
  |
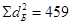 |
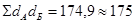 |
Вычислить средние арифметические величины для уровня физической работоспособности и результата гонки:
 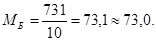
Найти отклонения показателей рядов "А" и "Б" от своих средних арифметических величин (dА
и dБ
). Например: для уровня ФР170
в 24,8 кГм/мин/кГ отклонения от среднего значения будут равны: 24,8 - 20,0 = + 4,8; для спортивного результата в 63 мин.: 63 - 73 = - 10 и т.д.
Вычислить квадраты найденных отклонений (dА
2
и dБ
2
). Получим: + 4,82
= 23,04; - 102
= 100.
Найти суммы квадратов отклонений: 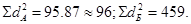
Определить произведения отклонений (dА
и dБ
). Получим: (+ 4,8) * ( - 10) = - 48.
Найти сумму произведений отклонений: SdА
dБ
= 174,9 » 175.
Подставить найденное значение в формулу:
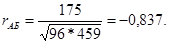
Определить достоверность высчитанного коэффициента корреляции.
Установлено, что если парных факторов меньше 100, то оценку достоверности целесообразно производить по таблице критических значений коэффициента корреляции.
Критические значения коэффициента корреляции r
Число
коррелируемых пар, п
|
Уровень значимости, Р
|
Число
коррелируемых
пар, п
|
Уровень значимости, Р
|
| 0,05 |
0,01 |
0,05 |
0,01 |
| 3 |
0,977 |
0,99988 |
19 |
456 |
575 |
| 4 |
950 |
990 |
20 |
444 |
561 |
| 5 |
878 |
959 |
21 |
433 |
549 |
| 6 |
811 |
917 |
22 |
423 |
537 |
| 7 |
754 |
874 |
25 |
396 |
505 |
| 8 |
707 |
834 |
30 |
361 |
463 |
| 9 |
666 |
798 |
35 |
332 |
435 |
| 10 |
632 |
765 |
40 |
310 |
407 |
| 11 |
602 |
735 |
45 |
292 |
384 |
| 12 |
576 |
708 |
50 |
277 |
364 |
| 13 |
553 |
684 |
60 |
253 |
353 |
| 14 |
532 |
661 |
70 |
234 |
308 |
| 15 |
514 |
641 |
80 |
219 |
288 |
| 16 |
497 |
623 |
90 |
206 |
272 |
| 17 |
482 |
606 |
100 |
196 |
258 |
| 18 |
468 |
590 |
Коэффициент корреляции признается статистически значимым с вероятностью ошибки <0,05, если r
>r
05
, и с вероятностью ошибки <0,01, если r
> r01
.
Табличные значения даны для двух уровней значимости: Р
= 0,05 и Р
= 0,01. Полученный коэффициент корреляции может считаться достоверным лишь в том случае, если его числовое значение превышает табличное значение хотя бы при уровне значимости Р
= 0,05 для данного числа парных факторов. В приведенном примере для 10 парных факторов табличные значения составляют: Р
05
+ = 0,623, Р01
= 0,765. Высчитанный коэффициент равен 0,837, т.е. он больше табличного значения при Р
= 0,01.
Если парных факторов больше 100, оценку достоверности коэффициента целесообразно рассчитывать по формуле средней ошибки коэффициента корреляции (mr
):
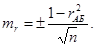
Принято считать, что достоверным коэффициент корреляции может быть признан только тогда, когда он превышает свою ошибку в 3 и более раза. В некоторых случаях формула может быть использована для оценки достоверности и при небольшом числе парных факторов, В данном примере:
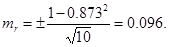
Полученный коэффициент корреляции превышает свою ошибку более чем в 8 раз.
Сделать методический вывод. Выявлена отрицательная корреляция: наиболее высоким показателям физической работоспособности соответствуют наименьшие показатели времени прохождения дистанции. Значит, чем более высоким уровнем физической работоспособности обладает спортсмен, тем лучше время (при прочих равных условиях) он может показать на дистанции.
Если на одном и том же материале высчитаны коэффициенты корреляции ρ и r, то необходимо провести сопоставление их значений по методу моментов Пирсона. Делается это следующим образом: определяется разница между абсолютными значениями двух коэффициентов без учета их знака.
0,837 - 0,807 = 0,030.
По В.Ю. Урбаху (1964) считается, что полученная разница не должна превышать 3%. В приведенном примере она составляет 0,025%, а поэтому находится в пределах нормы.
Коэффициент регрессии позволяет установить количественную меру изменения следственного фактора при изменении причинного фактора на одну единицу. В отличие от показателей корреляции - величин относительных, измеряющих тесноту связи между признаками в долях единицы, показатели регрессии - величины абсолютные: они характеризуют зависимость между переменными факторами по их абсолютным значениям (Г.Ф. Лакин" 1973).
Применительно к приведенному примеру вопрос в задаче на вычисление может быть сформулирован следующим образом: насколько в среднем улучшится спортивный результат в лыжной гонке при увеличении уровня физической работоспособности спортсменов на 1 кГм/мин/кг?
Чтобы получить ответ на поставленный вопрос, необходимо:
высчитать коэффициент корреляции r; оказалось, что он равен 0,837;
определить средние квадратические отклонения для каждого сравниваемого ряда; например, для ФР170
sA
оказалась равной 2,75, а для результатов в лыжной гонке sБ
- 6,14;
полученные значения подставить в формулу коэффициента регрессии R
АБ:
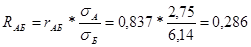 кГм/мин/кг/мин; кГм/мин/кг/мин;
сделать методический вывод: с увеличением уровня физической работоспособности на 1 кГм/мин/кг спортивный результат улучшался в среднем на 0,286 мин.
Коэффициенты регрессии особенно широко используются при изучении параметров физического развития детей, например для определения средней меры увеличения веса ребенка при увеличении его роста на 1 см.
В связи с тем, что расхождения между генеральными совокупностями определяются с помощью некоторых статистических параметров (средней арифметической величины, среднего квадратического отклонения и т.п.), полученных на выборочных совокупностях, t
критерий Стьюдента относится к так называемым параметрическим критериям (помимо этого критерия существуют и другие параметрические критерии).
Применять их целесообразно в тех случаях, когда собранные исследователем данные, во-первых, имеют количественную меру (т.е. выражены в каких-либо единицах измерения, например в метрах, секундах, баллах), во-вторых, образуют вариационный ряд, обладающий свойством нормального распределения, при котором колебание всех вариант в обе стороны от их средней арифметической величины примерно одинаковое, симметричное.
В педагогических исследованиях нередко возникает потребность рассчитать достоверность различий между небольшими совокупностями показателей, которые или имеют порядковый, а не количественный характер выражения (например, места, занятые спортсменами на соревновании), или не подчиняются закону нормального распределения (т.е. в вариационном ряду средняя арифметическая величина резко смещена в сторону больших или меньших вариант).
В таких случаях прибегают к использованию непараметрических критериев различия.
При выборе параметрических или непараметрических критериев следует иметь в виду, что наибольшей статистической мощностью (большей чувствительностью, лучшей разрешающей способностью) отличаются параметрические критерии (Г.Ф. Лакин, 1973). Поэтому в тех случаях, когда имеется вариационный ряд количественных показателей без явных признаков асимметричности, следует начинать обработку с помощью параметрических критериев. Если она даст результаты, далекие от граничных значений критерия, можно ими удовлетвориться; если же результаты окажутся на пределе значений достоверности, следует проверить, имеется ли достоверность различия, с помощью непараметрических критериев (не случайно их называют еще "вспомогательными критериями"). Подобное дублирование обработки никогда не окажется лишним, ибо затраты времени, кстати не столь уж значительные, окупятся большей достоверностью выводов.
Свое название непараметрические критерии получили потому, что не нуждаются в вычислении параметров, характеризующих те или иные выборки (среднего арифметического, среднего квадратического и т.п.). В связи с тем, что непараметрические критерии приложимы не только к вариантам с числовым выражением, но и к вариантам порядкового характера, их называют еще порядковыми критериями.
Непараметрические критерии в отличие от параметрических имеют простую конструкцию, не требуют большой вычислительной работы, могут оценивать вариационные; ряды порядкового характера любой формы распределения. Кроме того, они позволяют оценивать сравнительно небольшие выборки (кстати, даже таблицы значения критерия составлены на число вариант менее 30), что опять-таки чрезвычайно важно для педагогических исследований.
Существует несколько непараметрических критериев, в зависимости от конструкции и статистической мощности. Каждый из них специфичен в решении тех или иных задач исследования. Наиболее распространенными в педагогических и биологических исследованиях являются критерий Уайта и критерий Вилкоксона.
Критерий Уайта.
Условное обозначение этого критерия - Т. Он способен выявить различия между двумя совокупностями по их ведущим тенденциям, однако не оценивая степени колебания вариант. Поэтому две выборки с равно выраженными тенденциями, но с разными пределами колебаний будут квалифицированы критерием Уайта как одинаковые.
Критерий Уайта применим при сравнении одинаковых и разных по объему выборок.
Очередность числовых операций показана на примере исследования, задача которого определение эффективности методов разучивания двигательного действия по частям и в целом.
Полученные значения (в данном примере баллы, при разучивании по частям - V
r
- 8,0; 8,6; 8,5; 9,0; 9,6; 9,5; при разучивании в целом - V
Ц
-
8,1; 8,0; 8,2; 8,3; 8,7; 8,6; 9,4) в обеих выборках расположить в общий ряд в соответствии с их рангами в возрастающем порядке.
Чтобы облегчить последующие цифровые операции,, целесообразно построить ступенчатые ряды показателей и их рангов (R):
в верхнем ступенчатом ряду расположить полученные в исследовании показатели в возрастающем порядке, а в нижнем - их ранги:
vЧ
vЦ
|
8,08,5 8,69,09,5 9,6 -МЧ
= 8,87
8,0 8,1 8,2 8,38,6 8,79,4 -МЦ
= 8,47
|
RЧ
RЦ
|
1,56 7 51012 13 - ТЧ
= 50
1,5 3 4 5 7,5 911- ТЦ
= 41
|
Как видно, ступенчатый ряд показателей начинается с наименьшего показателя для обеих выборок, а затем перечисляются все остальные, причем на верхней "ступеньке" для одной выборки, а на нижней - для другой. Если в двух выборках встречаются равные показатели, то безразлично, какой из них будет стоять первым, а какой - вторым (из верхней половины ряда или из нижней), так как в этом случае ранг вычисляется путем деления суммы рангов, имеющих одинаковые значения показателей, на число таких одинаковых показателей. В данном примере показатели 8,0 и 8,0 занимают первое и второе места в общем, ступенчатом ряду и имеют одинаковый средний ранг 1.5 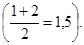
Создается впечатление, что оценки Vr
предпочтительнее, да и средняя арифметическая величина М
r
выше, чем М
ц
. На самом ли деле оценки Vr
выше, а следовательно, и метод разучивания по частям в данных условиях эффективнее, чем метод разучивания в целом, покажут следующие расчеты.
Вычислить суммы рангов Т
r
и T
ц
для рядов Rr
и R
ц
. В данном примере: Т
r
= 50, T
ц
= 41.
Проверить правильность вычисления суммы рангов рядов, для чего вычислить ее двумя способами:
а) Тч
+ T
ц
= 50 + 41 = 91;
б) 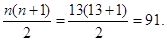
Подобная простая проверка чрезвычайно важна, так как от точности ранжирования зависит вывод о достоверности различия выборок.
Суммы рангов каждого ряда отличаются друг от друга на 9 единиц. Требуется определить, может ли эта разница считаться настолько значимой, чтобы говорить о большей эффективности одного из методов разучивания.
Для этого меньшую (обязательно меньшую!) сумму рангов (в данном случае 41) следует сравнить с табличным коэффициентом Т
по таблице "Значения критерия Уайта". Если Т
окажется больше меньшей суммы рангов, но не равной ей (Т
>41), то имеющаяся разность между двумя выборками считается достоверной.
Значения критерия Уайта при Р = 0,95 (по Д. Сепетлиеву, 1968)
Большее число наблюдений
|
Меньшее число наблюдений |
| 2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 4 |
11 |
| 5 |
6 |
11 |
17 |
| 6 |
7 |
12 |
18 |
26 |
| 7 |
7 |
13 |
20 |
27 |
36 |
| 8 |
3 |
8 |
14 |
21 |
29 |
38 |
49 |
| 9 |
3 |
8 |
15 |
22 |
31 |
40 |
51 |
63 |
| 10 |
3 |
9 |
15 |
23 |
32 |
42 |
53 |
65 |
78 |
| И |
4 |
9 |
16 |
24 |
34 |
44 |
55 |
68 |
81 |
96 |
| 12 |
4 |
10 |
17 |
26 |
35 |
46 |
58 |
71 |
85 |
99 |
115 |
| 13 |
4 |
10 |
18 |
27 |
37 |
48 |
60 |
73 |
88 |
103 |
119 |
137 |
| 14 |
4 |
И |
19 |
28 |
38 |
50 |
63 |
76 |
91 |
106 |
123 |
141 |
160 |
| 15 |
4 |
11 |
20 |
29 |
40 |
52 |
65 |
79 |
94 |
ПО |
127 |
145 |
164 |
185 |
| 16 |
4 |
12 |
21 |
31 |
42 |
54 |
67 |
82 |
97 |
114 |
131 |
150 |
169 |
| 17 |
5 |
12 |
21 |
32 |
43 |
56 |
70 |
84 |
100 |
117 |
135 |
154 |
| 18 |
5 |
13 |
22 |
33 |
45 |
58 |
72 |
87 |
103 |
121 |
139 |
| 19 |
5 |
13 |
23 |
34 |
46 |
60 |
74 |
90 |
107 |
124 |
| 20 |
5 |
14 |
24 |
35 |
48 |
62 |
77 |
93 |
НО |
| 21 |
6 |
14 |
25 |
37 |
50 |
64 |
79 |
95 |
| 22 |
6 |
15 |
26 |
38 |
51 |
66 |
82 |
| 23 |
6 |
15 |
27 |
39 |
53 |
68 |
| 24 |
6 |
16 |
28 |
40 |
55 |
| 25 |
6 |
16 |
28 |
42 |
| 26 |
7 |
17 |
29 |
| 27 |
7 |
17 |
Определить коэффициент Т
. Он определяется по числу вариант в каждом ряду. В данном примере n
ч
= 6, пц
= 7;
для данных объемов выборов табличный коэффициент Т
= 27 при пороге доверительной вероятности Р
= 0,95.
Сравнить табличный коэффициент Т
= 27 с меньшей суммой рангов: Т
= 27<41.
Сделать вывод. В данном примере: сравниваемые методы разучивания при данных условиях (виде разучиваемого двигательного действия, уровне подготовленности занимающихся квалификации преподавателя и т.п.) в принципе обладают одинаковой эффективностью. Более высокие оценки при методе разучивания по частям могут быть следствием каких-либо спонтанных факторов.
О некоторых частных вариантах использования критерия Уайта можно прочитать в книге В.Ю. Урбаха "Математическая статистика для биологов и медиков" (М., изд. АН СССР, 1963, стр.275 - 276).
Если полученное значение различия окажется очень близким к граничному значению табличного коэффициента, а следовательно, вызовет сомнение, то необходимо использовать более мощный, хотя и более громоздкий, критерий ван дер Вардена (он описывается во многих пособиях, в том числе и в названной книге В.Ю. Урбаха, стр.276 - 279).
Критерий Вликоксона.
Условное обозначение этого критерия - Z
. Он применяется в тех случаях, когда необходимо сравнить различия между парными вариантами, составляющими две выборки. Парных вариант должно быть не менее 6. Из критериев, с помощью которых можно решить подобные задачи, критерий Вилкоксона является наиболее статистически мощным, а по конструкции сравнительно простым. Именно поэтому он имеет наибольшее распространение.
Методика вычисления показана на примере лабораторного исследования, проведенного с целью установления сравнительной эффективности комплексов физических упражнений с волевым напряжением мышц. Одним из показателей, по которому оценивалась эффективность комплекса, являлось изменение силы мышц руки при сжатии динамометра. Было подобрано 9 идентичных; пар занимающихся, каждая из которых имела одинаковый исходный уровень динамометрии.
В каждой паре один занимающийся применял комплекс упражнений с волевым напряжением мышц ("силовой комплекс"), а второй - тот же самый комплекс упражнений, но без волевого напряжения мышц ("обычный комплекс").
Уравнивание пар на основе начальных показателей динамометрии позволяло (среди прочих способов обработки результатов) сравнить абсолютные значения конечных показателей динамометрии.
Очередность числовых операций:
Начертить сетку таблицы.
| Вид комплекса |
Динамометрия (кг) у сравниваемых пар |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Силовой
Обычный
Разница
Ранжирование
Ранги
|
55
54
1
0
|
60
61
1
1
2
|
56
56
0
1
2
|
63
61
2
1
2
|
59
57
2
2
4,5
|
62
63
1
2
4,5
|
65
62
3
3
6
|
58
64
6
6
7,5
|
66
60
6
6
6,5
|
Сумма рангов:
с отрицательными знаками
с положительными знаками
|
2 + 2 + 7,5 = 11,5
2 + 4,5 + 4,5 + 6 + 7,5 = 24,5
Итого36,0
|
Внести в графы "Силовой" и "Обычный" конечные значения динамометрии у каждой из 9 пар (например: 55 и 54 кг и т.д.).
Высчитать разницу между конечными значениями динамометрии, сохраняя при этом соответствующий знак (например: 60 - 61= - 1).
Провести ранжирование всех показателей разницы, начиная с наименьшего и кончая наибольшим. При этом учитываются лишь абсолютные значения разницы, т.е. чем больше разность, независимо от ее знака, тем больше должен быть ранг. В данном примере 1 и - 1 имеют одинаковый ранг 2 и меньший, чем у - 6.
Если в сравниваемой паре значения показателей равны (например: 56 и 56 кг), т.е. разница равна нулю, то они выпадают из дальнейших расчетов, и все вычисления должны производиться не из 9 сопряженных пар, а из 8.
Ранжированным показателям разницы присвоить соответствующие ранги. Если несколько показателей разницы имеют одинаковые значения (например: - 1, - 1 и 1), то каждому из них присваивается средний ранг, высчитываемый по правилу средней арифметической величины (например: 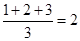 ; ранги в приведенном примере: 2; 2; 2 и т.д.). Высчитать суммы рангов отдельно с отрицательными и положительными знаками. В данном примере они равны 11, 5 и 24,5. Высчитать сумму всех рангов. В данном примере она равна 36. Проверить высчитанную сумму всех рангов по формуле: ; ранги в приведенном примере: 2; 2; 2 и т.д.). Высчитать суммы рангов отдельно с отрицательными и положительными знаками. В данном примере они равны 11, 5 и 24,5. Высчитать сумму всех рангов. В данном примере она равна 36. Проверить высчитанную сумму всех рангов по формуле:  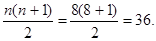
Значения критерия Вилкоксона для сопряженных рядов (
по В.Ю. Урбах, 1964)
| Число парных наблюдений |
Уровни значимости |
| 0,05 |
0,01 |
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
1
3
5
7
9
12
15
18
22
26
31
36
41
47
53
60
67
74
82
90
|
-
1
3
4
6
8
11
14
17
21
24
29
33
39
44
50
56
62
69
|
Определить табличный критерий z
для уровня значимости 0,05 и числа сравниваемых пар по таблице "Значения критерия Вилкоксона".
В приведенном примере для 8 парных наблюдений он будет равен 5.
Сравнить наименьшую сумму рангов (в данном примере 11,5) с табличным значением критерия z (
в данном примере 5): 2 = 5<11,5, т.е. меньше суммы рангов.
Разница в сопряженных парах считается достоверной, если табличное значение критерия больше полученной в исследовании меньшей суммы рангов. В приведенном примере оно оказалось меньшим, следовательно, между исследуемыми выборками нет достоверности различия.
Сделать педагогический вывод: при внешних признаках преимущества "силового" комплекса физических упражнений перед "обычным" комплексом оно не является достоверным по данным динамометрии при условии применения этих комплексов людьми, имеющими сходные характеристики с испытуемыми в данном исследовании.
Если число сопряженных пар в исследовании больше 25 (т.е. превышает число значений критерия, которые даны в таблице), то расчеты производятся иными способами (В.Ю. Урбах, 1963, стр.289).
1. Масальгин Н.А. Математико-статистические методы в спорте. М., ФиС, 1974.
2. Методика и техника статистической обработки первичной социологической информации. Отв. ред. Г.В. Осипов. М., "Наука", 1968.
3. Начинская С.В. Основы спортивной статистики. - К.: Вища шк., 1987. - 189 с.
4. Толоконцев Н.А. Вычисление среднего квадратического отклонения по размаху. Сравнение с общепринятым методом. Тезисы докладов третьего совещания по применению математических методов в биологии. ЛГУ, 1961, стр.83 - 85.
5. Фаламеев А.И., Выдрин В.М. Научно-исследовательская работа в тяжелой атлетике. ГДОИФК им. П.Ф. Лесгафта, 1974.
|