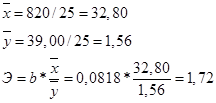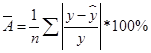Содержание
Задание 1
Задание 2
Использованная литература
Приложение
Таблица 1
Исходные данные
| потребительские расходы |
среднемесячная номинальная начисленная заработная плата |
| Белгородская область |
4678,7 |
8428,1 |
| Брянская область |
4464,1 |
6385,7 |
| Владимирская область |
3386,2 |
7515,5 |
| Воронежская область |
4913,2 |
6666,7 |
| Ивановская область |
3592 |
6545,2 |
| Калужская область |
5900,4 |
8483,8 |
| Костромская область |
3925 |
7492,4 |
| Курская область |
4992,4 |
7150,6 |
| Липецкая область |
5385,3 |
8617,1 |
| Московская область |
9030,4 |
11752,4 |
| Орловская область |
4338 |
6786,6 |
| Рязанская область |
4406,1 |
7763,1 |
| Смоленская область |
5128,7 |
7827,6 |
| Тамбовская область |
5196 |
6267,5 |
| Тверская область |
5875,9 |
8115,1 |
| Тульская область |
4464,8 |
7723,3 |
| Ярославская область |
5265,1 |
9012,8 |
| г.Москва |
22024,2 |
18698,6 |
По исходным данным выполнить корреляционный анализ:
1.1. Построить корреляционное поле и предложить гипотезу о связи исследуемых факторов;
1.2. Определить коэффициенты корреляции;
1.3. Оценить статистическую значимость вычисленных коэффициентов корреляции
1.4. Сделать итоговые выводы
Рис. 1. Поле корреляции
По полю корреляции можно сделать вывод о прямолинейной связи между потребительскими расходами и среднемесячной номинальной начисленной заработной платой
Для определения коэффициента корреляции может быть использована встроенная функция (=КОРРЕЛ(B4:B21;C4:C21)).
Так как коэффициент корреляции находится в диапазоне от 0,9 и более. То связь между потребительскими расходами и среднемесячной номинальной начисленной заработной платы весьма тесная
3.
Оценка статистической значимости коэффициента корреляции
Оценку статистической значимости коэффициента корреляции проведем с помощью t-статистики Стьюдента.
Выдвигаем гипотезу Н0
о статистически незначимом отличии показателей от нуля а0
=а1
=rху
=0.
tтабл
для числа степеней свободы df=n-2=18-2=16 и a=0,05 составит 2,12.
Расчетный коэффициент Стьюдента находятся по формуле:
Фактические значения t-статистики превосходят табличное значение на 5% -м уровне значимости при числе степеней свободы 16, tтабл
= 2,12. Таким коэффициент корреляции является статистически значимым Гипотеза Н0
не принимается.
Рассчитаем доверительный интервал:
 Таким образом, с вероятностью 95% можно утверждать, что коэффициент корреляции находится в диапазоне от 0,81 до 1.
Связь между потребительскими расходами и среднемесячной номинальной начисленной заработной платой прямолинейная и весьма тесная, это можно заключить исходя из распределения фактических значений по полю корреляции и расчетного значения коэффициента корреляции
Так как коэффициент корреляции находится в диапазоне от 0,9 и более, то связь между потребительскими расходами и среднемесячной номинальной начисленной заработной платы весьма тесная.
Коэффициент корреляции является статистически значимым с вероятностью 95% можно утверждать, что он находится в диапазоне от 0,81 до 1.
Таблица 3
Исходные данные
| № п/п |
Чистый доход, млрд долл. США, у |
Рыночная капитализация компании, млрд долл. США, х4 |
| 1 |
0,9 |
40,9 |
| 2 |
1,7 |
40,5 |
| 3 |
0,7 |
38,9 |
| 4 |
1,7 |
38,5 |
| 5 |
2,6 |
37,3 |
| 6 |
1,3 |
26,5 |
| 7 |
4,1 |
37 |
| 8 |
1,6 |
36,8 |
| 9 |
6,9 |
36,3 |
| 10 |
0,4 |
35,3 |
| 11 |
1,3 |
35,3 |
| 12 |
1,9 |
35 |
| 13 |
1,9 |
26,2 |
| 14 |
1,4 |
33,1 |
| 15 |
0,4 |
32,7 |
| 16 |
0,8 |
32,1 |
| 17 |
1,8 |
30,5 |
| 18 |
0,9 |
29,8 |
| 19 |
1,1 |
25,4 |
| 20 |
1,9 |
29,3 |
| 21 |
-0,9 |
29,2 |
| 22 |
1,3 |
29,2 |
| 23 |
2 |
29,1 |
| 24 |
0,6 |
27,9 |
| 25 |
0,7 |
27,2 |
По исходным данным выполнить регрессионный анализ:
2.1. Рассчитать параметры уравнения линейной парной регрессии;
2.2. Дать с помощью общего (среднего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом;
2.3. Оценить качество уравнения с помощью средней ошибки аппроксимации.
2.4. Оценить статистическую надежность результатов регрессионного моделирования с помощью критерия Стъюдента и F-критерия Фишера.
2.5. Сделать итоговые выводы.
Линейная модель: 
Расчеты для определения параметров модели произведены в MicrosoftExel.
Рис. 2.1. Результаты регрессионного анализа
В результате расчетов получаем уравнение регрессии:
При росте рыночной капитализации компании на 1 млр. руб. чистый доход возрастает на 0,0818 млрд. руб.
2. Расчет
общего (среднего) коэффициента эластичности
Коэффициент эластичности будем находить по следующей формуле:
Э=1,72 показывает, что чистый доход возрастает на 1,72% при росте рыночной капитализации компании на 1%.
Средняя ошибка аппроксимации находится как средняя арифметическая простая из индивидуальных ошибок по формуле:
Расчетные значения в среднем отличаются от фактических на 59%. Так как средняя ошибка аппроксимации превышает 10%, то полученную модель нельзя считать точной.
4.
Оценить статистическую надежность результатов регрессионного моделирования с помощью критерия Стъюдента и F-критерия Фишера
Так как значение коэффициента корреляции до 0,3 , то связь между чистым доходом и рыночной капитализацией компании слабая.
Оценку статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента.
Выдвигаем гипотезу Н0
о статистически незначимом отличии показателей от нуля а0
=а1
=rху
=0.
tтабл
для числа степеней свободы df=n-2=25-2=23 и a=0,05 составит 2,07.
Расчетные коэффициенты Стьюдента в Excel:
Фактические значения t-критерия меньше табличного значение на 5% -м уровне значимости при числе степеней свободы 23, tтабл
= 2,07. Таким образом коэффициенты статистическим не значимы. Гипотеза Н0
принимается.
Коэффициент детерминации равен квадрату коэффициента линейной корреляции
7% вариации чистого дохода объясняется вариацией рыночной капитализацией компании. А 93% вариацией других неучтенных факторов.
Критерий F-Фишера:
Табличное значение F- критерия при доверительной вероятности 0,95 при V1=k=1 и V2=n-k-1=25-1-1=23 составляет Fтабл =4,28.
Поскольку Fрас<Fтабл., то уравнение регрессии является не адекватным.
Уравнение линейной однофакторной зависимости рыночной капитализации компании от чистого дохода имеет вид:
Это означает, что при росте рыночной капитализации компании на 1 млр. руб. чистый доход возрастает на 0,0818 млрд. руб. Согласно расчету коэффициента эластичности чистый доход возрастает на 1,72% при росте рыночной капитализации компании на 1%.
Так как средняя ошибка аппроксимации превышает 10% (59%>10%), то полученную модель нельзя считать точной.
Значение коэффициента корреляции до 0,3 , то связь между чистым доходом и рыночной капитализацией компании слабая.
Параметры регрессии статистически не значимы. 7% вариации чистого дохода объясняется вариацией рыночной капитализацией компании. А 93% вариацией других неучтенных факторов. Поскольку Fрас<Fтабл., то уравнение регрессии является не адекватным.
1. Арженовский С.В., Федосова О.Н. Эконометрика: Учебное пособие/Рост, гос. экон. унив. - Ростов н/Д., - 2002.
2. Орлов А.И. Эконометрика: Учебник . – М.: Экзамен, 2002.
3. Практикум по эконометрике: Учебник /Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2003.
4. Федосеев В.В. и др. Экономико-математические методы и прикладные модели. М.: ЮНИТИ, 2001
5. Холод Н.И. Экономико-математические методы и модели. М.: 2003.
6. Эконометрика Учебное пособие /И.И. Елисеева. С.В. Курышева, Д.М. Гордиенко и др. - М.: Финансы и статистика, 2001.
7. Эконометрика: Учебник /Под ред. И.И.Елисеевой. – М.: Финансы и статистика, 2002.
Значение t-критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01
| Число степеней свободы |
Р |
| 0,10 |
0,05 |
0,01 |
| 1 |
6,3138 |
12,706 |
63,657 |
| 2 |
2,9200 |
4,3027 |
9,9248 |
| 3 |
2,3534 |
3,1825 |
5,8409 |
| 4 |
2,1318 |
2,7764 |
4,6041 |
| 5 |
2,0150 |
2,5706 |
4,0321 |
| 6 |
1,9432 |
2,4469 |
3,7074 |
| 7 |
1,8946 |
2,3646 |
3,4995 |
| 8 |
1,8595 , |
2,3060 |
3,3554 |
| 9 |
1,8331 |
2,2622 |
3,2498 |
| 10 |
1,8125 |
2,2281 |
3,1693 |
| 11 |
1,7959 |
2,2010 |
3,1058 |
| 12 |
1,7823 |
2,1788 |
3,0545 |
| 13 |
1,7709 |
2,1604 |
3,0123 |
| 14 |
1,7613 |
2,1448 |
2,9768 |
| 15 |
1,7530 |
2,1315 |
2,9467 |
| 16 |
1,7459 |
2,1199 |
2,9208 |
| 17 |
1,7396 |
2,1098 |
2,8982 |
| 18 |
1,7241 |
2,1009 |
2,8784 |
| 19 |
1,7291 |
2,0930 |
2,8609 |
| 20 |
1,7247 |
2,0860 |
2,8453 |
| 21 |
1,7207 |
2,0796 |
2,8314 |
| 22 |
1,7171 |
2,0739 |
2,8188 |
| 23 |
1,7139 |
2,0687 |
2,8073 |
| 24 |
1,7109 |
2,0639 |
2,7969 |
| 25 |
1,7081 |
2,0595 |
2,7874 |
| 26 |
1,7056 |
2,0555 |
2,7787 |
| 27 |
'1,7033 |
2,0518 |
2,7707 |
| 28 |
1,7011 |
2,0484 |
2,7633 |
| 29 |
1,6991 |
2,0452 |
2,7564 |
| 30 |
1,6973 |
2,0423 |
2,7500 |
| 40 |
1,6839 |
2,0211 |
2,7045 |
| 60 |
1,6707 |
2,0003 |
2,6603 |
| 120 |
1,6577 |
1,9799 |
2,6174 |
 |
1,6449 |
1,9600 |
2,5758 |
Значение F-критерия Фишера при уровне значимости 0,05
| V2 |
V1 |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 1 |
161 |
200 |
216 |
225 |
230 |
234 |
237 |
239 |
| 2 |
18,51 |
19,00 |
19,16 |
19,25 |
19,30 |
19,33 |
19,36 |
19,37 |
| 3 |
10,13 |
9,55 |
9,28 |
9,19 |
9,01 |
8,94 |
8,88 |
8,84 |
| 4 |
7,71 |
6,94 |
6,59 |
6,39 |
6,26 |
6,16 |
6,09 |
6,04 |
| 5 |
6,61 |
5,79 |
5,41 |
5,19 |
5,05 |
4.95 |
4,88 |
4,82 |
| 6 |
5,99 |
5,14 |
4.76 |
4.53 |
4,39 |
4,28 |
4,21 |
4,15 |
| 7 |
5,59 |
4,74 |
4,35 |
4,12 |
3,97 |
3,87 |
3,79 |
3,73 |
| 8 |
5,32 |
4,46 |
4,07 |
3,84 |
3,69 |
3,58 |
3,50 |
3,44 |
| 9 |
5,12 |
4,26 |
3,86 |
3,63 |
3,48 |
3,37 |
3,29 |
3,23 |
| 10 |
4,96 |
4,10 |
3,71 |
3,48 |
3,33 |
3,22 |
3,14 |
3,07 |
| 11 |
4,84 |
3,98 |
3,59 |
3,36 |
3,20 |
3,09 |
3,01 |
2,95 |
| 12 |
4,75 |
3,88 |
3,49 |
3,26 |
3,11 |
3,00 |
2,92 |
2,85 |
| 13 |
4,67 |
3,80 |
3,41 |
3,18 |
3,02 |
2,92 |
2,84 |
2,77 |
| 14 |
4,60 |
3,74 |
3,34 |
3,11 |
2,96 |
2,85 |
2,77 |
2,70 |
| 15 |
4,54 |
3,68 |
3,29 |
3,06 |
2,90 |
2,79 |
2,70 |
2,64 |
| 16 |
4,49 |
3,63 |
3,24 |
3,01 |
2,85 |
2,74 |
2,66 |
2,59 |
| 17 |
4,45 |
3,59 |
3,20 |
2,96 |
2,81 |
2,70 |
2,62 |
2,55 |
| 18 |
4,41 |
3,55 |
3,16 |
2,93 |
2,77 |
2,66 |
2,58 |
2,51 |
| 19 |
4,38 |
3,52 |
3,13 |
2,90 |
2,74 |
2,63 |
2,55 |
2,48 |
| 20 |
4,35 |
3,49 |
3,10 |
2,87 |
2,71 |
2,60 |
2,52 |
2,45 |
| 21 |
4,32 |
3,47 |
3,07 |
2,84 |
2,68 |
2,57 |
2,49 |
2,42 |
| 22 |
4,30 |
3,44 |
3,05 |
2,82 |
2,66 |
2,55 |
2,47 |
2,40 |
| 23 |
4,28 |
3,42 |
3,03 |
2,80 |
2,64 |
2,53 |
2,45 |
2,38 |
| 24 |
4,26 |
3,40 |
3,01 |
2,78 |
2,62 |
2,51 |
2,43 |
2,36 |
| 25 |
4,24 |
3,88 |
2,99 |
2,76 |
2,60 |
2,49 |
2,41 |
2,34 |
| 26 |
4,22 |
3,37 |
2,98 |
2,74 |
2,59 |
2,47 |
2,39 |
2,32 |
| 27 |
4,21 |
3,35 |
2,96 |
2,73 |
2,57 |
2,46 |
2,37 |
2,30 |
| 28 |
4,20 |
3,34 |
2,95 |
2,71 |
2,56 |
2,44 |
2,36 |
2,29 |
| 29 |
4,18 |
3,33 |
2,93 |
2,70 |
2,54 |
2,43 |
2,35 |
2,28 |
| 30 |
4,17 |
3,32 |
2,92 |
2,69 |
2,53 |
2,42 |
2,34 |
2,27 |
| 35 |
4.12 |
3.26 |
2.87 |
2.64 |
2.48 |
2.37 |
2.28 |
2.22 |
| 40 |
4,08 |
3,23 |
2,84 |
2,61 |
2,45 |
2,34 |
2,25 |
2,18 |
| 50 |
4,03 |
3,18 |
2,79 |
2,56 |
2,40 |
2,29 |
2,20 |
2,13 |
| 60 |
4,00 |
3,15 |
2,76 |
2,52 |
2,37 |
2,25 |
2,17 |
2,10 |
| 100 |
3,94 |
3,09 |
2,70 |
2,46 |
2,30 |
2,19 |
2,10 |
2,03 |
|