Реферат: Симплекс-метод 2

Название: Симплекс-метод 2
Раздел: Рефераты по математике
Тип: реферат

МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

«МАТИ» — РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ им. К.Э. ЦИОЛКОВСКОГО

Кафедра «Моделирование систем и информационные технологии»

«СИМПЛЕКС-МЕТОД»

Преподаватель: Смирнов Н. Я.

Студент: Асосков А.В.

Группа: 14АСУ-3ДС-025

Вариант: 3

2010 г.

Часть 1. Введение

В последние годы в прикладной математике большое внимание уделяется новому классу задач оптимизации, заключающихся в нахождении в заданной области точек наибольшего или наименьшего значения некоторой функции, зависящей от большого числа переменных. Это так называемые задачи математического программирования, возникающие в самых разнообразных областях человеческой деятельности и прежде всего в экономических исследованиях, в практике планирования и организации производства. Изучение этого круга задач и методов их решения привело к созданию новой научной дисциплины, получившей позднее название линейного программирования. В конце 40-х годов американским математиком Дж. Данцигом был разработан эффективный метод решения данного класса задач – симплекс-метод. К задачам, решаемых этим методом в рамках математического программирования относятся такие типичные экономические задачи как «Определение наилучшего состава смеси», «Задача об оптимальном плане выпуска продукции», «Оптимизация межотраслевых потоков», « Задача о выборе производственной программы», «Транспортная задача», «Задача размещения», «Модель Неймана расширяющейся экономики» и другие. Решение таких задач дает большие выгоды как народному хозяйству в целом, так и отдельным его отраслям.

Решение задач математического программирования при помощи симплекс-метода традиционными способами требует затрат большого количества времени. В связи с бурным развитием компьютерной техники в последние десятилетия естественно было ожидать, что вычислительная мощность современных ЭВМ будет применена для решения указанного круга задач.

Симплекс метод – является универсальным методам, которым можно решить любую задачу линейного программирования.

Часть 2. Основная

Математическое описание метода.

Допустим, имеется система уравнений ограничений:

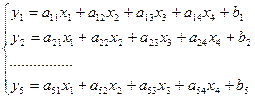
Допустим, требуется вывести из числа свободных переменных какую – либо переменную, например, х₂ и перевести ее в базисную, а в замен ее ввести в число свободных какую то базисную, например у₃ , т. е. х₂ ↔у₃ . Если проводить этот процесс математическим способом то, необходимо было бы переразрешать каждое уравнение в системе ограничений относительно новой свободной переменной, т. е. новое получившееся уравнение, в котором была произведена замена необходимо подставить во все остальные уравнения, а так же целевую функцию. Данная процедура является громоздкой, поэтому проще задачу решить с помощью определенного алгоритма и записывать все промежуточные результаты в таблицу. Чтобы этот алгоритм был проще и лучше запоминался необходимо произвести следующие преобразования:

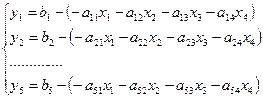
Избавляемся от отрицательных коэффициентов, для этого принимаем

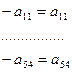
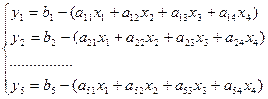
Данная форма записи уравнений называется стандартной.

СЧ	х₁	х₂	х₃	х₄
у₁	b₁	a₁₁	a₁₂	a₁₃	a₁₄
у₂	b₂	a₂₁	a₂₂	a₂₃	a₂₄
у₃	b₃	a₃₁	a₃₂	a₃₃	a₃₄
у₄	b₄	a₄₁	a₄₂	a₄₃	a₄₄
у₅	b₅	a₅₁	a₅₂	a₅₃	a₄₅

При пересечении разрешающей строки у₃ и разрешающего столбца х₂ получаем разрешающий элемент а_32.

Необходимо найти коэффициенты, которые получатся в разрешающей строке после обмена х₂ ↔ у₃ _.

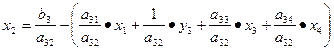
СЧ	х₁	у₃	х₃	х₄
у₁
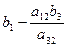
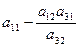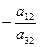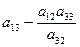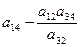y₂
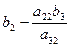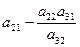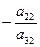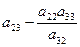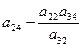x₂
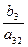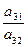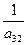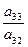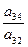y₄
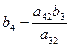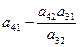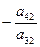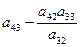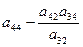y₅

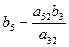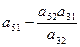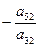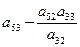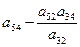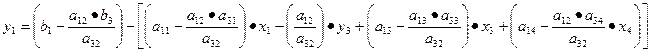
Алгоритм преобразования коэффициентов стандартной таблицы.

Разрешающий элемент заменяется на обратную ему величину.
Все остальные элементы разрешающей строки делятся на разрешающий элемент.
Все элементы разрешающего столбца, кроме самого разрешающего элемента делятся на разрешающий элемент и меняют знак.
Каждый из остальных элементов подвергается следующему преобразованию: к нему прибавляется произведение элементов, стоявшего в прежней разрешающей строке на том же месте по порядку (т. е. в том же столбце), на элемент стоящий в новом разрешающем столбце на соответствующем месте (т. е. в той же строке, что и рассчитываемый элемент).

При всей легкости данных вычислений более удобно все промежуточные расчеты писать в той же таблице.

Алгоритм преобразования x _j ↔ y_i стандартной таблицы сводится к следующим операциям:

1. Выделить в таблице разрешающий элемент. Вычислить ее обратную величину 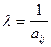и записать в нижней части этой же ячейки, например в правом нижнем углу.

2. Все элементы разрешающей строки, кроме самого разрешающего элемента умножить на 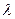, результат записать в нижней части той же ячейки.

3. Все элементы разрешающего столбца, кроме всего разрешающего элемента умножить на – a, записать в нижней части той же ячейки.

4. Подчеркнуть в разрешающей строке все верхние числа (прежние элементы) за исключением самого разрешающего элемента. А в разрешающем столбце все новые элементы, кроме самого разрешающего элемента.

5. Для каждого из элементов не принадлежащих ни к разрешающей строке, ни к разрешающему столбцу в нижней часть ячейки записать произведение выделенных чисел, стоящих в той же строке и в том же столбце, что и данный элемент.

6. Переписать таблицу, заменив:

· x_j наy_i ;

· элемент разрешающей строки и столбца, числами, стоящими в нижней части тех же ячеек;

· каждый из остальных элементов суммой чисел стоящей в верхней и нижней части той же ячейки.

В любой задаче ОЗЛП существует так же линейная функция L, которая в общем случае выглядит следующим образом:

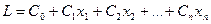
Для решения ее табличным способом ее так же можно привести к стандартному виду.

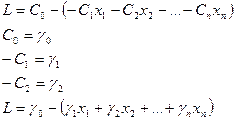
Таким образом, в стандартной таблице появляется еще одна строка L. С ней производятся только такие же вычисления как со всеми остальными ячейками таблицы, строка L никогда не может быть разрешающей строкой. С помощью табличного алгоритма обмена переменных в управлениях ОЗЛП можно решить любую задачу линейного программирования или убедиться, что она не имеет решения.

Нахождение решения каждой задачи распадается на два этапа:

1. нахождение опорного плана;

2. отыскание оптимального решения.

В процессе первого этапа выясняется, имеет ли данная задача допустимые не отрицательные решения, если да, то находиться опорное решение, для которого все остальные переменные равны 0, а все базисные не отрицательные.

В процессе второго этапа выясняется, ограничена ли снизу функция L, которая стремиться к минимуму, если нет, то оптимального решения не существует. Если да, то оно отыскивается после замены x на y.

Двойственные задачи ОЗЛП.

В процессе расчета задачи ОЗЛП может получиться один или несколько отрицательных свободных членов, это означает, что полученное решение не является опорным, соответственно не может быть оптимальным. Рассмотрим случай, когда среди свободных членов есть отрицательный. Для того, чтобы избавиться от них необходимо пересчитать таблицу обмена базисных и свободных переменных пока не придем к опорному решению или не убедимся в том, что решение не существует. Необходимо так обменивать базисные и свободные переменные, чтобы эта процедура приближала к области допустимых решений, чтобы число отрицательных свободных членов убывало или по крайне мере убывали их абсолютные величины.

Допустим, имеется одно из уравнений с отрицательным свободным членом:

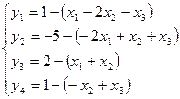
СЧ		x₁		x₂		x₃
y₁	1	2	-1	1	-2	1	-1	0
y₂	-5	4	-2	2	1	2	1	0
y₃	2	2	1	1	1	1	0	0
y₄	1	0	0	0	-1	0	1	0

Ищем в данной строке (y₂ ) отрицательный элемент a_ij ,если такого элемента нет, то данная система уравнений не совместна. При отсутствии отрицательных элементов в строке вся правая часть соответствующего уравнения может быть только отрицательной, а это противоречит условиям не отрицательных переменных.

Если такой элемент есть, то выбираем столбец, в котором он находиться в качестве разрешающего. Далее необходимо найти сам разрешающий элемент. Для рассмотрения берем в данном столбце только те элементы, которые имеют одинаковый знак со свободным членом. Находим отношения свободного члена и элемента в той же строке и среди полученных отношений берем min по модулю, таким образом находиться разрешающая строка.

СЧ	x₁	x₂	x₃
y₁	3	2	1	2
y₂	1	2	3	-1
y₃	2	1	-1	0
y₄	1	0	-1	0

Блок – схема алгоритма.

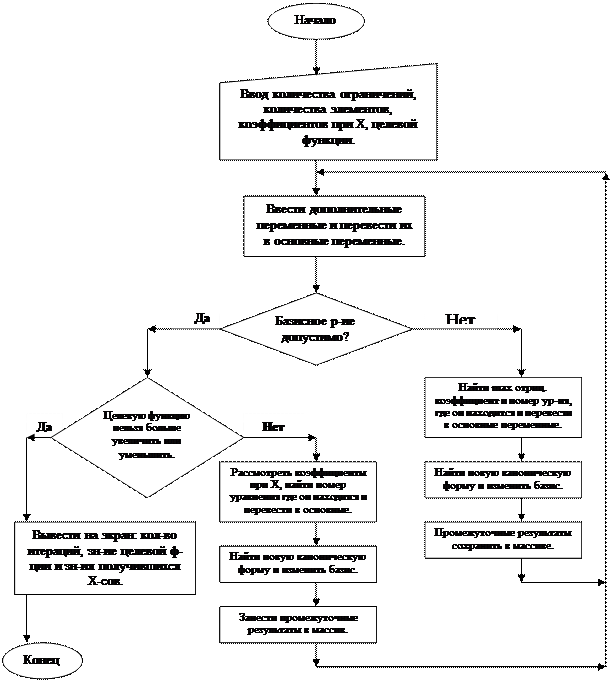
Пример решения задачи с использованием симплекс-метода.

Даны данные: из которых составляется система уравнений вида:

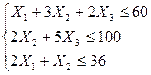
Целевая функция этой системы уравнений стремится в максимум, и имеет вид:

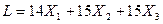
Базисное решение является допустимым, так как в правой части неравенств не содержатся отрицательные значения.

В данной системе 3 – уравнения с 3 – неизвестными, принимают за основные X₄ , X_5, X₆ – переменных.

После этого выражают основные переменные (добавочные) через неосновные, и находят базисное решение соответствующее.

Вводим добавочные неотрицательные переменные (которые еще называют «неосновные»), и сводим систему неравенств к эквивалентной системе уравнений.

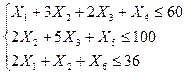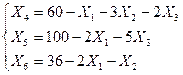
Так как в полученной системе уравнений нет отрицательных свободных членов, то базисное решение является допустимым (0; 0; 0; 60; 100; 36).

Выразим целевую функцию через неосновные переменные: для этого находят абсолютные величины отношений свободных членов уравнений, к коэффициентам при переменной, переводимой в основные, причем только из тех уравнений, в которых эти коэффициенты положительны.

Х₂ : {60/1; 100/1; 36/1} переводим Х₂ в основные переменные: из третьего уравнения, так как 36/1=36 наименьший коэффициент.

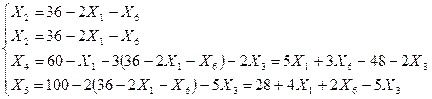
Подставим в целевую функцию =>Х₂ :

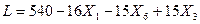
Рассмотрим полученную систему уравнений и целевую функцию:

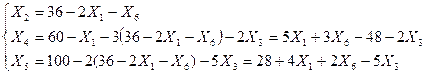
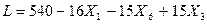
Если отыскивается максимум линейной формы, и в ступени выражений нет основных переменных с положительным знаком, то критерий оптимальности выполнен и полученное базисное решение служит оптимальным (задача решена), но в примере еще есть две переменные с положительным знаком.

Переходим к новому базисному решению {0; 5; 0; 0; 20; 50}. Из не основных переменных, входящих в линейную форму (уравнения) с положительным коэффициентом выбираем ту, которой соответствует наибольший коэффициент и переводит ступени в основные.

Рассмотрим переменную Х₁ {10; 10; 17}. Выразим из первого уравнения переменную Х₁ :

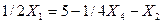
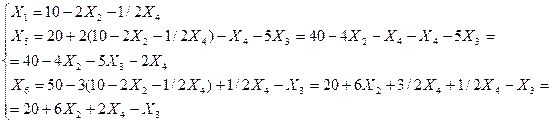
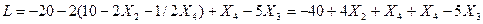
Рассмотрим полученную систему уравнений и целевую функцию:

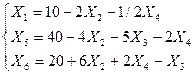
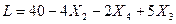
Если отыскивается максимум линейной формы, и в ступени выражений нет основных переменных с положительным знаком, то критерий оптимальности выполнен и полученное базисное решение служит оптимальным (задача решена), но в примере еще есть одна переменная с положительным знаком (Х₃ ).

Переходим к новому базисному решению {10; 0; 0; 0; 40; 20}. Из не основных переменных, входящих в линейную форму с положительным коэффициентом выбираем Х₃ , которой соответствует наибольший коэффициент (5) и переводит ступени в основные.

Рассмотрим переменную Х₃ {0; 8; 20}. Выразим из второго уравнения переменную Х₃ :

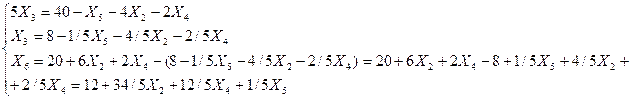
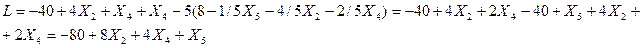
Рассмотрим полученную систему уравнений и целевую функцию:

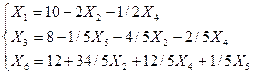
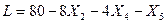
Отыскивается максимум линейной формы, так как в ступени выражений нет основных переменных с положительным знаком – критерий оптимальности выполнен и полученное базисное решение служит оптимальным (задача решена).

То есть при Х₁ =10; Х₂ =0; X₃ =8 максимальное значение функции равно 80 (Lmax=80).

Листингпрограммы.

Program Simplex_Metod;

Uses crt;

label

POVZNAC, NACH;

var

Fo, FunctPr, B, H, Hnew, C, Cnew, CPr, Cprnew, FX: array[1..30] of real;

X, Xnew: array[1..30,1..30] of real;

BS, Bvsp,ZNAC: array[1..30] of string[3];

MIN, I1, I, J, Kx, Ky, Kit, NachKell, NachY, K_st: integer;

PriznacY, KLstr, KLst, ErrCode, Dop_X: integer;

P, P1, Mo, F0, Epsilon, Z, CHLEN: real;

VSP, S, PrOper: string;

F: text;

DPx, DPy, MinMax, Kell, SNom: integer;

Function MakeIndex (V:integer; S:char): string;

var

M,Z: string;

begin

STR(V,M);

Z:=S+M;

MakeIndex:=Z;

end;

Procedure enter;

var

BUF :string;

NEXT :boolean;

begin

clrscr;

repeat

write ('Введите количество уравнений: ');

readln (SNom);

if (SNom > 10) or (SNom <=0) then

begin

writeln ('Введите число 1 до 10: ');

readln;

end

else NEXT:=True;

until NEXT;

repeat

NEXT:=False;

write ('Количество элементов: ');

readln (Kell);

if (Kell > 10) or (Kell <=0) then

begin

writeln (Введите число от 1 до 10: ');

readln;

end

else NEXT:=True;

until NEXT;

NachKell:=Kell;

DPx:=Kell+1;

DPy:=1;

Epsilon:=0.00001;

for I:=1 to SNom do

begin

for J:=1 to Kell do

begin

write ('Введите ',J,'-й элемент ',I,'-го уравнения: ');

readln (Xnew [I,J]);

end;

repeat

write ('Введите знак: ');

readln (ZNAC [I]);

if (ZNAC [I] <> '>=') and (ZNAC [I] <> '=') and (ZNAC [I] <> '<=') then

begin

write ('Неправильно задан знак!');

readln;

end;

if (ZNAC [I] = '=') or (ZNAC [I] = '>=') then PriznacY:=1;

until (ZNAC [I] = '>=') or (ZNAC [I] = '=') or (ZNAC [I] = '<=');

write ('Введите свободный член: ');

read (B[I]);

end;

write ('Введите свободный член целевой функции: ');

readln (CHLEN);

for J:=1 to Kell do

begin

write ('Введите ',J,'-й коэффициент целевой функции: ');

read (FX[J]);

end;

readln;

write ('Целевая функция стремится к максимуму (Д/Н): ');

readln (BUF);

if (BUF='Д') or (PrOper='Д') then MinMax:=1

else MinMax:=2;

write ('Целочисленное решение (Д/Н): ');

readln (PrOper);

if (PrOper='Д') or (PrOper='Д') then PrOper:='Д'

else PrOper:='Н';

end;

procedure DOP_PER;

begin

if ZNAC[I1]='=' then

begin

Kell:=Kell+1;

Bvsp[Kell]:=MakeIndex (DPy, 'Y');

DPy:=DPy+1;

Xnew[I1,Kell]:=1;

if MinMax=1 then FX [Kell]:=-1

else FX [Kell]:=1;

FunctPr[Kell]:=1;

for I:=1 to SNom do

if I<>I1 then Xnew [I,Kell]:=0;

end;

if ZNAC[I1]='>=' then

begin

Kell:=Kell+1; Bvsp[Kell]:=MakeIndex(DPx,'X');

DPx:=Dpx+1; Dop_X:=Dop_X+1;

Xnew[I1,Kell]:=-1; FX[Kell]:=0;

for I:=1 to SNom do

if I<>I1 then Xnew[I,Kell]:=0;

Kell:=Kell+1; Bvsp[Kell]:=MakeIndex(DPy,'Y');

DPy:=DPy+1;

Xnew[I1,Kell]:=1;

if MinMax=1 then FX[Kell]:=-1

else FX[Kell]:=1;

FunctPr[Kell]:=1;

for I:=1 to SNom do

if I<>I1 then Xnew[I,Kell]:=0;

end;

if ZNAC[I1]='<=' then

begin

Kell:=Kell+1; Bvsp[Kell]:=MakeIndex(DPx,'X');

DPx:=DPx+1; Dop_X:=Dop_X+1;

Xnew[I1,Kell]:=1; FX[Kell]:=0;

for I:=1 to SNom do

if I<>I1 then Xnew[I,Kell]:=0;

end;

procedure SOKR;

var

P:integer;

begin

Kell:=Kell-1;

for P:=NachKell+DOP_X to Kell do

if Bvsp[P]=BS[KLstr] then

begin

for J:=P to Kell do Bvsp[J]:=Bvsp[J+1];

FunctPr[J]:=FunctPr[J+1];

FX[J]:=FX[J+1];

for I:=1 to SNom do Xnew[I,J]:=Xnew[I,J+1];

end;

procedure OPER;

var

MAX, Z:real;

begin

KLstr:=1;

MAX:=H[1]-INT(H[I1]);

for I1:=2 to SNom do

if (H[I1]-int(H[I1]))>=MAX then

begin

MAX:=H[I1];

KLstr:=I1;

end;

SNom:=SNom+1;

Hnew[SNom]:=H[KLstr]-INT(H[KLstr]);

for I1:=1 to Kell do

begin

Z:=INT(X[KLstr,I1]);

if X[KLstr,I1]<0 then Z:=Z-1;

Xnew[SNom,I1]:=X[KLstr,I1]-Z;

end;

ZNAC[SNom]:='>=';

end;

begin

clrscr;

Kit:=0;

Dop_X:=0;

Kx:=1;

Ky:=3;

enter;

for J:=1 to Kell do Bvsp[J]:=MakeIndex(J,'X');

for I1:=1 to SNom do DOP_PER;

MIN:=0;

if (MinMax=1) and (PriznacY=1) then

begin

MIN:=MinMax;

MinMax:=2;

for J:=1 to Kell do FX[J]:=-FX[J];

end;

for I1:=NachKell+1 to Kell do

for J:=I1+1 to Kell do

if Bvsp[J]<Bvsp[I1] then

begin

VSP:=Bvsp[J]; Bvsp[J]:=Bvsp[I1]; Bvsp[I1]:=VSP;

P:=FX[J]; FX[J]:=FX[I1]; FX[I1]:=P;

P:= FunctPr[J]; FunctPr[J]:=FunctPr[I1]; FunctPr[I1]:=P;

for I:=1 to SNom do

begin

P:=Xnew[I,I1];

Xnew[I,I1]:=Xnew[I,J];

Xnew[I,J]:=P;

end;

Kit:=1;

clrscr;

for I:=1 to SNom do

begin

Hnew[I]:=B[I];

for J:=NachKell+1 to Kell do

if Xnew[I,J]=1 then

begin

BS[I]:=Bvsp[J];

Cnew[I]:=FX[J];

CPrnew[I]:=FunctPr[J];

end;

NACH:;

repeat

PriznacY:=0;

for I:=1 to SNom do

begin

if INT(10000*Hnew[I])=0 then H[I]:=+0

else H[I]:=Hnew[I];

C[I]:=Cnew[I];

CPr[I]:=CPrnew[I];

if BS[I][1]='y' then PriznacY:=1;

for J:=1 to Kell do

if INT(10000*Xnew[I,J])=0 then X[I,J]:=+0

else X[I,J]:=Xnew[I,J];

end;

for J:=1 to Kell do Fo[J]:=0;

F0:=0;

for J:=1 to Kell do Fo[J]:=0;

for I1:=1 to SNom do

begin

if PriznacY=1 then

if BS[I1][1]='Y' then

begin

F0:=F0+H[I1];

for J:=1 to Kell do Fo[J]:=Fo[J]+X[I1,J];

end;

if PriznacY=0 then

begin

F0:=F0+H[I1]*C[I1];

for J:=1 to Kell do Fo[J]:=Fo[J]+C[I1]*X[I1,J];

end;

for J:=1 to Kell do

if Bvsp[J][1]='Y' then Fo[J]:=+0

else

if ABS(Fo[J])<Epsilon then Fo[J]:=+0;

end;

for J:=1 to Kell do

if PriznacY<>1 then Fo[J]:=Fo[J]-FX[J];

P:=0;

for J:=1 to Kell do

if MinMax=1 then

if Fo[J]<-Epsilon then

begin

P:=1;

continue;

end

else

if Fo[J]>Epsilon then

begin

P:=1;

continue;

end;

if P<>1 then

begin

writeln('В ', Kit,'-й итерации было получено оптимальное решение');

for I1:=1 to SNom do

if BS[I1][1]='Y' then

begin

writeln('Но так как из базиса не введены все Y, то ');

writeln('можно сделать вывод, что РЕШЕНИЙ НЕТ');

exit;

end;

for I:=1 to SNom do

begin

Z:=round(H[I]);

if ABS(Z-H[I])<Epsilon then H[I]:=round(H[I]);

for J:=1 to Kell do

begin

if X[I,J]<0 then Z:=round(X[I,J]);

if ABS (Z-X[I,J])<Epsilon then X[I,J]:=round(X[I,J]);

end;

P1:=0;

for I:=1 to SNom do

begin

if INT(10000*FRAC(H[I]))<>0 then

begin

P1:=1;

continue;

end;

for J:=1 to Kell do

if BS[I]=Bvsp[J] then

for I1:=1 to SNom do

if ABS (FRAC(X[I1,J]))>=Epsilon then

begin

P:=1;

continue;

end;

if (PrOper='Y') and (P1=1) then

begin

oper;

NachKell:=Kell;

I1:=SNom; DPy:=1;

DOP_PER;

BS[SNom]:=Bvsp[Kell];

CPrnew[SNom]:=FunctPr[Kell];

Cnew[SNom]:=FX[Kell];

goto NACH;

end;

ifP1=0 thenwriteln('Решение целочисленное.');

if MIN=1 then

begin

F0:=-F0;

MinMax:=MIN;

end;

KLst:=1; Mo:=0;

for J:=1 to Kell do

if MinMax=1 then

if Fo[J]<Mo then Mo:=Fo[J];

for J:=1 to Kell do

begin

if Bvsp[J][1]<>'Y' then

if MinMax=1 then

begin

if Fo[J]<0 then

if Fo[J]>=Mo then

begin

Mo:=Fo[J]; KLst:=J;

end;

end

else

begin

if Fo[J]>0 then

if Fo[J]>=Mo then

begin

Mo:=Fo[J];

KLst:=J;

end;

P1:=0; K_st:=0;

for J:=1 to Kell do

if ABS(Mo-Fo[J])<Epsilon then

begin

K_st:=K_st+1;

for I:=1 to SNom do

if X[I,KLst]>0 then

begin

B[I]:=H[I]/X[I,KLst];

P:=B[I];

KLstr:=I;

end

else

begin

B[I]:=-1;

P1:=P1+1;

end;

if P1=SNom*K_st then

begin

writeln('Решений нет, так как невозможно определить ключевую строку');

exit;

end;

P1:=0;

for J:=1 to Kell do

if ABS (Mo-Fo[J])<Epsilon then

for I:=1 to Snom do

if B[I]>=0 then

begin

if B[I]<P then

if Bvsp[KLst]<>BS[I] then

begin

P:=B[I];

KLstr:=I;

end;

if INT(10000*B[I])=INT(10000*P) then

if (BS[I][1]='Y') and (BS[KLstr][1]='X') then

if Bvsp[KLst]<>BS[I] then

begin

P:=B[I];

KLstr:=I;

end;

for I:=1 to SNom do

if Bvsp[KLst]=BS[I] then

begin

writeln('Решений нет, так как в базисном столбце уже есть ');

writeln('такая переменная.');

exit;

end;

if CPr[KLstr]=1 then SOKR;

BS[KLstr]:=Bvsp[KLst];

Cnew[KLstr]:=FX[KLst];

CPrnew[KLstr]:=FunctPr[KLst];

for I:=1 to SNom do

begin

if I=KLstr then Hnew[I]:=H[I]/X[KLstr,KLst]

else Hnew[I]:=H[I]-(H[KLstr]*X[I,KLst]/X[KLstr,KLst]);

for J:=1 to Kell do

begin

if (I=KLstr) and (J=KLst) then Xnew[I,J]:=1;

if (I=KLstr) and (J<>KLst) then Xnew[I,J]:=X[I,J]/X[KLstr,KLst];

if (I<>KLstr) and (J=KLst) then Xnew[I,J]:=0;

if (I<>KLstr) and (J<>KLst) then Xnew[I,J]:=X[I,J]-(X[KLstr,J]*X[I,KLst]/X[KLstr,KLst]);

end;

repeat

KLst:=0;

KLstr:=0;

Kit:=Kit+1;

until (Kit=0);

end;

end.

Часть 3. Тестовые примеры.

Пример №1.

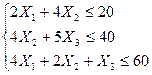
Целевая функция этой системы уравнений стремится в максимум, и имеет вид:

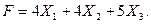
Программа выводит данные:

В 4-й итерации было получено оптимальное решение.

Результат решения:

Fmax=80

X₁ =10

X₃ =8

X₆ =12

Пример №2.

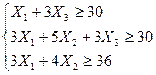
Целевая функция этой системы уравнений стремится в минимум, и имеет вид:

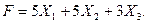
Программа выводит данные:

В 6-й итерации было получено оптимальное решение.

Результат решения:

Fmin=75

X₃ =10

X₂ =9

X₅ =45

Часть 4. Заключение.

В курсовой работе проделана работа по изучению следующих вопросов:

Рассмотрен и дан алгоритм симплекс метода.
Разработана программа для решения разного рода задач, ее можно применить в различных отраслях, а также были составлены текстовые примеры, показывающие простоту и экономичность работы.
Инструкции пользователю не нужны, так как данная программа проста и практически не требует времени на освоение.

Данная программа имеет простой интерфейс, не требует дополнительных ресурсов в виде свободного места на диске. Все вычисления производятся только в оперативной памяти. Тесты, не выявили ни каких отклонений в ходе решения программой поставленных задач.

Программа имеет ограничения: количество рассмотренных уравнений и вводимых элементов уравнения не должно превышать 10.

Программа не рассчитана на неправильный ввод формата вводимых данных.

Часть 5. Литература.

1. Зайченко Ю.П., Шумилова С.А. Исследование операций.

2. Лищенко «Линейное и нелинейное программирование», М. 2003

3. А.Н. Карасев, Н.Ш. Кремер, Т.Н. Савельева «Математические методы в экономике», М.2000

4. Орлов А.И. Теория принятия решений. Учебное пособие. - М.: Издательство "Март", 2004

5. Интернет