ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОУ ВПО «НИЖНЕВАРТОВСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ»
Факультет информационных технологий и математики
Отделение математики и информатики
050201.65 «Математика с дополнительной специальностью информатика»
ДЕДИНЕЦ Анна Владимировна
МЕТОД КЕЙСОВ КАК СРЕДСТВО ФОРМИРОВАНИЯ ПОЗНАВАТЕЛЬНОГО ИНТЕРЕСА УЧАЩИХСЯ ПРИ ИЗУЧЕНИИ ТЕМЫ «ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ» В 10 КЛАССЕ
Выпускная квалификационная работа
| Допустить к защите
: |
Научный руководитель
|
| Зав. кафедрой _________________ |
Доцент |
| Научный руководитель _________ |
Абрамова Нина Васильевна |
| ______________________________ |
Рецензент:
________________________ |
| ___________________________________ |
| ___________________________________ |
Нижневартовск 2010
Оглавление
Введение.2
Глава 1.2
Теоретические основы проблемного изложения материала как средства формирования познавательного интереса учащихся.2
§1. Методы обучения.2
1. Метод. Классификация методов.2
2. Проблемные методы.2
3. Метод кейсов.2
§2. Познавательный интерес.2
1. Познавательный интерес. Уровни развития познавательного интереса.2
2. Средства формирования познавательного интереса.2
3. Активизация познавательной деятельности учащихся.2
Глава 2.2
Методика формирования познавательного интереса учащихся с помощью кейс-метода при изучении темы «Преобразование тригонометрических выражений» в 10 классе.2
§1. Цели и содержание темы «Преобразование тригонометрических выражений».2
§2. Система кейс-заданий по теме «Преобразование тригонометрических выражений», направленная на формирование познавательного интереса.2
§3. Тематическое планирование.2
§4. Методика изучения темы «Преобразование тригонометрических выражений».2
Глава 3.2
Экспериментальное исследование.2
§1. Констатирующий этап эксперимента.2
§2. Диагностирующий этап эксперимента (16.11.09 – 21.11.09).2
§3. Формирующий этап эксперимента (23.11.09 – 12.12.09).2
§4. Диагностирующий этап эксперимента (14.12.09 – 19.12.09).2
Заключение.2
Глоссарий.2
Список литературы.2
Приложение 1. 2
Приложение 2. 2
Приложение 3. 2
Приложение 4. 2
Приложение 5. 2
Приложение 6. 2
Приложение 7. 2
Приложение 8. 2
Приложение 9. 2
Приложение 10. 2
Приложение 11. 2
Приложение 12. 2
Приложение 13. 2
Приложение 14. 2
Приложение 15. 2
Приложение 16. 2
Приложение 17. 2
Приложение 18. 2
Приложение 19. 2
Приложение 20. 2
Предмет математики настолько серьёзен,
что надо не упускать случая, сделать его
занимательным
Б.Паскаль
Концепция модернизации Российского образования на период до 2010 года и правительственная стратегия модернизации содержания общего образования предполагает использовать компетентностный подход, четкую ориентацию на будущее, которая проявляется в возможности построения своего образования с учетом успешности в личностной и профессиональной деятельности, в свое время которая может быть достигнута под действием активизации познавательного интереса.
Под познавательным интересом понимают избирательную направленность личности, обращенную к области познания, к ее предметной стороне и самому процессу овладения знаниями.
Проблемой формирования познавательного интереса школьников занимались такие ученые, как Г.И. Щукина, В.Н. Липник, В.А. Филиппова, И.Г. Шапошникова, А.И. Герцен, Н.И. Пирогов, К.Д. Ушинский, Л.Н. Толстой, А.С. Макаренко. Рассмотрены взаимосвязи формирования познавательных интересов с процессом становления личности школьника и проблемами совершенствования урока. Неоценим вклад в эту область Я.И. Перельмана.
В современной науке и мировом образовании, включая российское, на всех его уровнях представлен широкий спектр инноваций – проблемных, имитационных, исследовательских, игровых, компьютерных, проективных, контекстных и других моделей обучения.
Одним из интереснейших новых и специфических методов является метод кейсов. Суть данного метода состоит в том, что учебный материал подается учащимся в виде ситуаций (кейсов), а знания приобретаются в результате активной и творческой исследовательской работы.
Этот метод широко используется в экономическом, юридическом, медицинском, бизнес образовании и других. Он имеет ряд преимуществ, так как позволяет: 1) приобрести навыки применения теоретических знаний для анализа практических проблем; 2)приобрести навыки ясного и точного изложения собственной точки зрения в устной или письменной форме; 3)выработать умение убедительно обосновывать и защищать свою точку зрения; 4) научиться принимать самостоятельные решения на основе группового анализа ситуации; 5) научиться извлекать пользу из своих и чужих ошибок, опираясь на данные обратной связи.
Но в школьном образовании, и, в частности, при обучении учащихся математике, метод кейсов не получил широкого применения.
На это существует ряд причин:
- отсутствие в достаточной мере специальной литературы о применении кейс-метода в обучении математике;
- отсутствие методики составления кейсов;
- отсутствие у преподавателя опыта проведения занятий методом кейсов и др.
Проблема исследования
заключается в противоречии между необходимостью внедрения метода кейсов в процесс обучения учащихся, направленного на формирование познавательного интереса, и отсутствием соответствующих методических разработок по конкретным темам школьного курса математики.
Объект исследования
– учебный процесс, направленный на формирование познавательного интереса.
Предмет исследования
– методика формирования познавательного интереса методом кейсов на уроках алгебры и начал анализа при изучении темы «Преобразование тригонометрических выражений».
Цель данной работы
:
Разработать методику изучения темы «Преобразование тригонометрических выражений», направленную на формирование познавательного интереса на уроках алгебры в 10 классе методом кейс-технологии.
Задачи:
1. Изучить психолого-педагогическую литературу по теме исследования;
2.Проанализировать действующие программы и учебники;
3.Разработать методику изучения темы «Преобразование тригонометрических выражений» методом кейсов, направленную на формирование познавательного интереса.
4. Провести экспериментальное обучение по разработанной методике в 10 А классе МОСШ № 32 г. Нижневартовска, учитель математики Одобеско Нина Михайловна.
Гипотеза исследования
: разработанная методика будет способствовать росту сознательного отношения к учению, развитию познавательных процессов, умению ими управлять, сознательно их регулировать, что в свою очередь будет способствовать повышению уровня знаний.
Для решения поставленных задач использовались следующие методы исследования
:
1.Теоретические методы: анализ психолого-педагогической и методической литературы, учебных программ, нормативных документов, учебников и учебных пособий; изучение и обобщение опыта учителей.
2.Эмпирические методы: наблюдение, опрос, беседа, анкетирование, интервьюирование, экспериментальное обучение.
3.Статистические методы: количественная и качественная обработка материалов, сравнение и шкалирование.
Практическая значимость
: составлена система заданий, направленная на формирование познавательного интереса; разработана система уроков (13 фрагментов), направленная на формирование выделения проблемы, ее анализа, нахождения путей решения и их реализации.
Данная работа состоит из введения, трех глав, заключения, списка литературы, приложений и глоссария.
Первая глава посвящена объекту исследования. В ней проводится анализ различных определений понятий: «познавательный интерес», «средства обучения», «метод» и их классификаций. Выделены уровни познавательного интереса. Рассмотрены проблемные методы, метод кейсов и его основные положения и принципы, выделены этапы решения кейсов.
Вторая глава посвящена предмету исследования. Выполнен анализ программ и учебников по математике, представлено тематическое планирование, методика формирования познавательного интереса учащихся с помощью кейс-метода при изучении темы «Преобразование тригонометрических выражений» и фрагменты уроков
Третья глава посвящена экспериментальному исследованию. Выполнен анализ интервью и анкетирования. Сделаны выводы по проведенному исследованию.
В заключении описывается результат исследования, и делаются выводы.
Список литературы содержит __ источников. 20 приложений.
Внедрение материалов исследования осуществлялось в МОСШ № 32 г. Нижневартовска, учитель математики Одобеско Нина Михайловна.
Процесс обучения невозможен без использования методов.
«Метод(от греческого слова «metodos» — буквально путь к чему-либо) означает способ достижения цели, определенным образом упорядоченную деятельность» [22, С – 1]. «Методом обучения называют способ упорядоченной взаимосвязанной деятельности преподавателя и обучаемых, деятельности, направленной на решение задач образования, воспитания и развития в процессе обучения» [8, С – 1].В процессе обучения метод выступает как способ взаимосвязанной деятельности учителя и учащихся по достижению определенных учебно-воспитательных целей. Метод обучения включает в себя обучающую работу учителя и организацию активной учебно-познавательной деятельности учащихся.
Существуют разные классификации методов по различным признакам. Рассмотрев классификации С.И. Перовского и Е.Я. Голанта, М.А. Данилова и Б. П. Есипова, М.Н. Скаткина и И.Я. Лернера, М.И. Махмутова и других, мы попытались их систематизировать и составили таблицу.
| №
|
Признак
|
Классификация
|
| 1 |
По источникам передачи и характеру восприятия информации (С.И. Перовский, Е.Я. Голант). |
1. Словесные;
2. Наглядные;
3. Практические.
|
| 2 |
В зависимости от основных дидактических задач (М.А. Данилов, Б.П. Есипов). |
1. Методы приобретения знаний;
2. Методы формирования умений и навыков;
3. Методы применения знаний;
4. Методы творческой деятельности;
5. Методы закрепления;
6. Методы проверки знаний, умений, навыков.
|
| 3 |
В соответствии с характером познавательной деятельности учащихся по усвоению содержания образования (М.Н. Скаткин, И.Я. Лернер). |
1. Объяснительно-иллюстративный (информационно-рецептивный) метод;
2. Репродуктивный метод;
3. Проблемное изложение;
4. Частично-поисковый или эвристический метод;
5. Исследовательский метод.
|
| 4 |
По сочетанию методов преподавания с соответствующими методами учения (М.И. Махмутов). |
1. Информационно-обобщающий и исполнительский метод;
2. Объяснительный и репродуктивный метод;
3. Инструктивно-практический и продуктивно-практический метод;
4. Объяснительно-побуждающий и частично-поисковый метод;
5. Побуждающий и поисковый метод.
|
| 5 |
По рассмотрению четырех сторон методов (С.Г. Шаповаленко). |
1. Логико-содержательные методы;
2. Источниковые методы;
3. Процессуальные методы;
4. Организационно-управленческие методы.
|
| 6 |
По целостному подходу. |
1. Методы организации и осуществления учебно-познавательной деятельности;
2. Методы стимулирования и мотивации учебно-познавательной деятельности;
3. Методы контроля и самоконтроля за эффективностью учебно-познавательной деятельности.
|
Все чаще применяются подходы к классификации методов обучения одновременно по источникам знаний и логическим обоснованиям (Н. М. Верзилин), по источникам знаний и уровню самостоятельности учащихся в учебной деятельности (А. Н Алексюк, И. Д. Зверев и др.).
Из таблицы видно, что классификации методов по различным признакам тесно связаны между собой. Но, несмотря на их многообразие, каждый из методов наиболее эффективен при определенных условиях организации процесса обучения, при выполнении определенных дидактических функций.
Рассмотрев различные классификации методов проблемного обучения, мы составили таблицу.
| №
|
Признак
|
Виды методов
|
| 1 |
По способу решения проблемных задач. |
1. Проблемное изложение;
2. Совместное обучение;
3. Исследование;
4. Творческое обучение.
|
| 2 |
По характеру взаимодействия и распределению активности педагога и учащихся. |
1. Сообщающий и исполнительный;
2. Объяснительный и репродуктивный;
3. Инструктивный и практический;
4. Объяснительно-побуждающий и частично-поисковый;
5. Побуждающий и поисковый.
|
| 3 |
По организации процесса проблемного обучения. |
1. Объяснительно-иллюстративный метод;
2. Репродуктивный метод;
3. Метод проблемного изложения;
4. Частично-поисковый или эвристический метод;
5. Исследовательский метод.
|
Остановимся более подробно на классификации методов проблемного обучения, предложенной М.И. Махмутовым, названных им дидактическими способами организации процесса проблемного обучения. Это объяснительно-иллюстративный метод, репродуктивный метод, метод проблемного изложения, частично-поисковый или эвристический и исследовательский метод.
М.И. Махмутов в зависимости от способа представления учебного материала (проблемных ситуаций) и степени активности учащихся выделял шесть методов: метод монологического изложения, рассуждающий метод изложения, диалогический метод изложения, эвристический метод обучения, исследовательский метод и метод программированных заданий. Первые три из них представляют варианты изложения учебного материала учителем, вторые три – варианты организации самостоятельной учебной деятельности учащихся. В каждой из этих групп методов и в классификации в целом предполагается увеличение активности учащихся и, таким образом, проблемности обучения.
Эвристический метод обучения в концепции М.И. Махмутова заключается в том, что учебный материал разбивается на отдельные элементы, в которых учителем дополнительно ставятся определенные познавательные задачи, разрешаемые непосредственно учащимися.
В случае применения исследовательского метода структура и последовательность подачи материала остается такой же, как и в эвристическом методе, но постановка вопросов учителем осуществляется не вначале изучения проблемы, а уже по итогам ее самостоятельного рассмотрения учащимися, то есть деятельность учителя носит не направляющий характер, а оценочный, констатирующий.
И последний метод, который выделял М.И. Махмутов, был назван им методом программированных действий или программированных заданий. При этом методе педагогом осуществляется разработка целой системы программированных заданий, в которой каждое задание состоит из отдельных элементов (или «кадров»).
Современная концепция модернизации российского образования предполагает использование таких методов, как проблемный, исследовательский, проективный, контекстный и другие. В рамках контекстного метода выделяют новый и специфический метод – метод кейсов.
«Метод кейсов или метод конкретных ситуаций – метод активного проблемно-ситуационного анализа, основанный на обучении путем решения конкретных задач – ситуаций (решение кейсов)» [8, С – 1].
Кейсовый метод обучения начал применяться еще в начале ХХ века в области права и медицины. Ведущая роль в распространении кейсового метода принадлежит Гарвардской Школе Бизнеса. В период с 1909 по 1919 гг. обучение происходило по схеме, когда учеников просили изложить конкретную ситуацию (проблему), а затем дать анализ проблемы и соответствующие рекомендации. Первый сборник кейсов был издан в 1921 г. (Dr. Copeland. DeanDonhman).
«Слово «ситуация», пришедшее из французского языка, включает в себя следующие значения: 1) положение, расположение; 2)поставленный, положенный, лежащий; 3) обитающий, живущий» [11, С – 1].
«Ситуация (от средневекового лат. situatio – положение) – сочетание условий и обстоятельств, создающих определенную обстановку, положение» [31, С – 1].
По словарю Ожегова, ситуация – совокупность обстоятельств, положение, обстановка.
В различных источниках понятие ситуации несет один и тот же смысл. Но существует такое понятие, как педагогическая ситуация.
«Педагогическая ситуация – это факт, жизненная история, с которой учитель столкнулся в повседневной работе и которая породила педагогические задачи, требующие решения» [29, С – 1]. Одни педагогические ситуации (штатные) встречаются часто, они позволяют в процессе анализа действий учащихся быстро сформулировать педагогические задачи, решить их и ликвидировать эти ситуации. Другие (нештатные) – редко встречающиеся, сложные, неповторимые, требующие длительного времени для своего разрешения, а иногда и вовсе не разрешимые.
В основе каждой педагогической ситуации лежит конфликт:
– недовольство (отрицательное отношение к кому-нибудь или чему-нибудь);
– разногласие (отсутствие согласия из-за несходства во мнениях, взглядах);
– противодействие (действие, препятствующее другому действию);
– противостояние (сопротивление действию кого-нибудь, чего-нибудь);
– разрыв (нарушение связи, согласованности между чем-нибудь, кем-нибудь).
Работа учителя над разрешением педагогических ситуаций складывается из нескольких взаимосвязанных действий: 1) обнаружение факта; 2) описание (конструирование) конкретной педагогической ситуации; 3) определение характера ее содержания; 4) анализ педагогической ситуации; 5) формулирование педагогических задач, выявление наиболее значимых; 6) дополнительная теоретическая и практическая подготовка учителя к решению возникших педагогических задач; 7) выбор способов решения педагогических задач; 8) самоанализ и самооценка принятого решения.
Махмутов М.И. [20] выделяет следующую классификацию педагогических ситуаций: 1) по месту возникновения и протекания (на уроке, вне урока, на улице, дома и т.д.); 2) по степени проективности (преднамеренно созданные, естественные, стихийные, спроектированные); 3) по степени оригинальности (стандартные, нестандартные, оригинальные); 4) по степени управляемости (жестко заданные, неуправляемые, управляемые); 5) по участникам (ученик-ученик, ученик-учитель и т.д.); 6) по заложенным противоречиям (конфликтные, бесконфликтные, критические); 7) по содержанию (проблемные, политехнические, производственно-технические).
Одним из видов педагогической ситуации является проблемная ситуация.
Проблемная ситуация в педагогике рассматривается как состояние умственного затруднения, вызванного в определенной учебной ситуации объективной недостаточностью ранее усвоенных учащимися знаний и способов умственной или практической деятельности для ответа на возникший познавательный вопрос, в психологии – как состояние интеллектуального напряжения, связанного с неожиданным "препятствием для хода мысли" [29, С – 1].
«Такое обучение формирует у учащихся, зачастую бессознательно, понимание и способность мышления на языке основных проблем, с которыми они столкнутся в своей деятельности» [17, С - 284].Метод кейсов способствует развитию умения: 1) анализировать ситуации, 2) оценивать альтернативы, 3) выбирать оптимальный вариант и 4) составлять план его осуществления. И если в течение учебного года такой подход применяется многократно, то у учащихся вырабатывается устойчивый навык решения практических задач.
Последовательность действий учителя состоит: в подборе соответствующего реального материала; ученики должны разрешить поставленную проблему и получить реакцию окружающих (других учеников и учителя) на свои действия. «При этом нужно помнить, что возможны различные решения проблемы. Учащиеся должны понимать с самого начала, что риск принятия решений лежит на них» [17, С - 284]. Роль учителя состоит в том, чтобы направить беседу или дискуссию в нужное русло, например, с помощью проблемных вопросов, проконтролировать время работы, побудить учащихся отказаться от поверхностного мышления.
«В кейсе рассматривается конкретная ситуация, в описание которой включаются случаи, факты, решения, имевшие место в течение определенного времени» [17, С - 285]. Причем, ситуация может отражать как комплексную проблему, так и частную задачу.
Информация не представляет собой полного описания процесса или события, а скорее носит ориентирующий характер. «Поэтому для построения логичной модели, необходимой для принятия обоснованного решения, допускается дополнять кейс данными, которые, по мнению участников, могли иметь место в действительности» [17, С - 285]. Таким образом, ученик не только фиксирует рассматриваемый случай, но и вникает в него до такой степени, что может прогнозировать и демонстрировать то, что пропущено в кейсе.
Опираясь на исследования У.Д. Таймасханова [28], можно выделить следующие приемы создания проблемных ситуаций:
1) Прием приведения контрпримеров – примеров, опровергающих некоторое утверждение.
2) Прием неправильного решения представленной задачи.
3) Прием прогнозирования невозможности решения задачи.
4) Прием неверной подсказки.
5) Прием незавершенного задания.
6) Прием истолкования математической ситуации в реальной жизни.
7) Прием открытия нового через анализ ситуации окружающего мира (конкретно-индуктивный способ введения нового материала).
В.А. Козырева, Н.Ф. Радионова, А.П. Тряпицына выделяют пять ключевых критериев, по которым можно отличить кейс от другого учебного материала:
1.Источник. Источником создания любого кейса являются люди, которые вовлечены в определенную ситуацию, требующую решения.
2.Процесс отбора информации. При отборе информации для кейса необходимо ориентироваться на учебные цели. Не существует единых подходов к содержанию данных, но они должны быть реальными для сферы, которую описывает кейс, иначе он не сможет возбудить интереса учеников, так как будет казаться нереальным.
3. Содержание. Содержание кейса должно отражать учебные цели. Кейс может быть коротким или длинным, может содержать материал конкретный или обобщенный. Следует избегать чрезмерно насыщенной информации или информации, напрямую не относящейся к рассматриваемой теме. В целом кейс должен содержать дозированную информацию, которая позволила бы ученику быстро войти в проблему и получить все необходимые данные для ее решения.
4.Проверка. «Проверка – это апробация нового кейса непосредственно в учебном процессе или оценка реакции новой аудитории на кейс, который раньше рассматривался, но в других классах» [5, С – 1]. Изучение реакции на кейс необходимо для получения максимального учебного результата.
5.Процесс устаревания. Большинство кейсов постепенно устаревает, поскольку новая ситуация требует новых подходов. «Материалы, основанные на истории, хорошо слушаются, но работа с ними происходит неактивно, поскольку «это было уже давно»» [5, С – 2]. Проблемы, рассмотренные в кейсе, должны быть актуальны для сегодняшнего дня.
Существует широкий круг целей обучения, из числа которых можно выбрать цели для курса с использованием кейсового метода.
Примеры возможных образовательных целей кейсового метода: приобретать знания; развивать общие представления; понимать методы; приобретать навыки использования метода, концепции и знания; приобретать навыки анализа сложных и неструктурированных проблем; приобретать навыки разработки действий и их осуществления; учиться слушать; развивать определенные отношения; нести ответственность за свои решения, результаты; развивать определенные качества ума; развивать умение общаться – коротко, эффективно, убедительно; достигать ясности целей и задач; уметь обобщать – от конкретных деталей к осознанию перспектив и разработке успешных концепций.
Классификация кейсов может производиться по различным признакам. Одним из широко используемых подходов к классификации кейсов является их сложность:
1) иллюстративные учебные ситуации – кейсы, цель которых – на определенном практическом примере обучить учеников алгоритму принятия правильного решения в определенной ситуации. При изучении темы «Многогранники» детям предлагается исследовать макеты различных выпуклых многогранников, сформулировать проблемы и решить их;
2) учебные ситуации – кейсы с формированием проблемы, в которых описывается ситуация в конкретный период времени. Выявляются и четко формулируются проблемы; цель такого кейса – диагностирование ситуации и самостоятельное принятие решения по указанной проблеме. При изучении темы «Прямоугольный треугольник» детям предлагается решить задачу: «В Древнем Египте после разлива Нила требовалось восстановить границы земельных участков, для чего на местности необходимо было уметь строить прямые углы. Египтяне поступали следующим образом: брали веревку, завязывали на равных расстояниях узлы и строили треугольники со сторонами, равными 3, 4 и 5 таких отрезков. Правильно ли они поступали?»;
3) учебные ситуации – кейсы без формирования проблемы, в которых описывается более сложная ситуация, где проблема четко не выявлена, а представлена в статистических данных, оценках общественного мнения, органов власти и т.д.; цель такого кейса – самостоятельно выявить проблему, указать альтернативные пути ее решения с анализом наличных ресурсов. При изучении темы «Многогранники» детям предлагается придумать задачу по изображенному параллелепипеду, на котором указаны некоторые данные;
4) прикладные упражнения, в которых описывается конкретная сложившаяся ситуация. Предлагается найти пути выхода из нее; цель такого кейса – поиск путей решения проблемы. При изучении темы «Признак перпендикулярности плоскостей» детям предлагается проанализировать и найти выход из ситуации: «Стены зданий возводятся вертикально. Как стены должны быть расположены по отношению к полу? Как же строители осуществляют контроль над этим?».
«Кейсы могут быть классифицированы, исходя из целей и задач процесса обучения» [10, С – 5]. В этом случае могут быть выделены следующие типы кейсов: 1) обучающие анализу и оценке; 2) обучающие решению проблем и принятию решений; 3) иллюстрирующие проблему, решение или концепцию в целом.
Заслуживает внимания классификация кейсов, приведенная Н. Федяниным и В. Давиденко, хорошо знакомыми с зарубежным опытом использования кейс-метода: 1) структурированный (highlystructured) кейс, в котором дается минимальное количество дополнительной информации; при работе с ним ученик должен применить определенную модель или формулу; у задач этого типа существует оптимальное решение; 2) «маленькие наброски» (shortvignetts), содержащие от одной до десяти страниц текста и одну-две страницы приложений; они знакомят только с ключевыми понятиями, и при их разборе ученик должен опираться еще и на собственные знания; 3) большие неструктурированные кейсы (longunstructuredcases) объемом до 50 страниц – самый сложный из всех видов; информация в них дается очень подробная, иногда ненужная; самые необходимые сведения могут отсутствовать; ученик должен распознать такие «подвохи» и справиться с ними; 4) первооткрывательские кейсы (groundbreakingcases), ученики и учитель выступают в роли исследователей.
Кейсы бывают «мертвые» и «живые». К «мертвым» кейсам можно отнести кейсы, в которых содержится вся необходимая для анализа информация. «Чтобы «оживить» кейс, необходимо построить его так, чтобы спровоцировать учеников на поиск дополнительной информации для анализа» [26, С – 16].
По наличию сюжета кейсы делятся на сюжетные и бессюжетные.
Бывают кейсы с приложениями и без приложений; кейсы с приложениями обычно предполагают формирование навыков расчетов и анализа статистической информации.
По типу методической части кейсы бывают вопросными, при их разрешении ученикам нужно дать ответы на поставленные вопросы. Бывают кейсы-задания, которые формулируют задачу или задание.
На основе классификаций мы составили таблицу.
| №
|
Признак
|
Виды методов
|
| 1 |
По сложности. |
1. Иллюстративные учебные ситуации;
2. Учебные ситуации с формированием проблемы;
3. Учебные ситуации без формирования проблемы;
4. Прикладные упражнения.
|
| 2 |
По целям и задачам процесса обучения. |
1. Обучающие анализу и оценке;
2. Обучающие решению проблем и принятию решений;
3. Иллюстрирующие проблему, решение или концепцию в целом.
|
| 3 |
По Н. Федянину и В. Давиденко. |
1. Структурированный (highlystructured) кейс;
2. «Маленькие наброски» (shortvignetts);
3. Большие неструктурированные кейсы (longunstructuredcases);
4. Первооткрывательские кейсы (groundbreakingcases).
|
| 4 |
По наличию сюжета. |
1. Сюжетные;
2. Бессюжетные.
|
| 5 |
По количеству информации. |
1. «Мертвые»;
2. «Живые».
|
| 6 |
По типу методической части. |
1. Вопросные;
2. Кейсы-задания.
|
Опыт показывает, что кейс превращается тогда в эффективное учебно-методическое произведение, когда получает всестороннюю не только научную и методическую, но и жанровую проработку.
Целесообразно выделение следующих основных этапов создания кейсов:
1. Формирование дидактических целей кейса. Этот этап включает определение места кейса, раздела дисциплины, формулирование целей и задач, выявление знаний, умений и навыков учащихся.
2. Определение проблемной ситуации.
3. Построение программной карты кейса, состоящей из основных тезисов, которые необходимо воплотить в тексте.
4. Сбор информации относительно тезисов программной карты кейса.
5. Построение или выбор модели ситуации, которая отражает тему, проверка ее соответствия реальности.
6. Выбор жанра кейса.
7. Написание текста кейса.
8. Диагностика, проведение эксперимента для выяснения эффективности данного кейса.
9. Подготовка окончательного варианта кейса.
10. Внедрение кейса в практику обучения при проведении учебных занятий, публикации с целью распространения.
11. Подготовка методических рекомендаций по использованию кейса: разработка заданий, вопросов для дискуссии и презентации кейса, действия учащихся и учителя.
Требования к кейсам:
- кейс должен быть написан интересно, простым и доходчивым языком;
- отличаться «драматизмом» и проблемностью;
- выразительно определять «сердцевину» проблемы;
- показывать как положительные примеры, так и отрицательные;
- соответствовать потребностям выбранного контингента учащихся;
- содержать необходимое и достаточное количество информации.
Определение и классификация проблемы занимает исключительно важное место в процессе конструирования модели ситуации. Вместе с тем текст кейса не должен подсказывать ни одного решения относительно поставленной проблемы.
Решение кейсов рекомендуется проводить в пять этапов:
Первый этап – знакомство с ситуацией, ее особенностями.
Второй этап – выделение основной проблемы (основных проблем), выделение факторов и персоналий, которые могут реально воздействовать.
Третий этап – предложение концепций или решений проблемы.
Четвертый этап – анализ последствий принятия того или иного решения.
Пятый этап – решение кейса – предложение одного или нескольких вариантов (последовательности действий), указание на возможное возникновение проблем, механизмы их предотвращения и решения.
Анализ кейсов может быть как специализированным, так и всесторонним. Специализированный анализ должен быть сосредоточен на конкретном вопросе или проблеме. Всесторонний (подробный) анализ подразумевает глубокое погружение в ключевые вопросы кейса.
Основными этапами применения кейс технологии на уроках математики являются: 1) подготовка и предоставление учителем учебно-методического материала по изучаемой теме каждому ученику; 2) планомерная и последовательная работа с учащимися по проработке каждого вопроса темы, предполагающая как самостоятельное изучение ребенком отдельных вопросов, так и работу в классе или индивидуальные консультации; 3) обязательное обобщение изучаемой темы учителем, выявление пробелов в изучении отдельных вопросов темы и их устранение; 4) диагностика по окончании изучения темы или раздела.
Положительные стороны кейс-технологии: ученик видит сразу весь объем материала, который необходимо знать по данной теме; даже в случае болезни ребенок видит пропущенные им вопросы и может поработать над ними самостоятельно; ребенок может планировать время работы над данной темой; у части учащихся появляется желание подготовиться к обобщающему уроку как можно лучше для того, чтобы выступить в роли консультанта для одноклассников, что непременно оценивается учителем; к концу учебного года у ученика набирается полный набор учебно-методических материалов по всем изученным за год темам, который он может использовать для повторения и подготовки к экзаменам.
Активное обучение, которое осуществляется с помощью методов обучения, способствует формированию познавательного интереса к приобретению знаний и учебной деятельности.
«Познавательный интерес – это глубинный внутренний мотив, основанный на свойственной для человека врожденной познавательной потребности» [32, С – 1]. Наличие интереса является одним из главных условий успешного протекания учебного процесса и свидетельством его правильной организации.
Исследованием понятия «познавательный интерес» в разное время занимались различные авторы: С.Л. Рубинштейн, Ф.Н. Гоноболин, Г.И. Щукина, И.Ф. Харламов и другие. Рассмотрим некоторые определения этого понятия.
«Особая избирательная направленность личности на процесс познания, избирательный характер которой выражается в той или иной предметной области», - С.Л. Рубинштейн.
«Стремление человека обращать на что-то внимание, познавать какие-либо предметы и явления», - Ф.Н. Гоноболин.
«Особое избирательное, наполненное активным замыслом, сильными эмоциями, устремлениями отношения личности к окружающему миру, к его объектам, явлениям, процессам», - Г.И. Щукина.
«Эмоционально окрашенная потребность, прошедшая стадию мотивации и придающая деятельности человека увлекательный характер», - И.Ф. Харламов.
Рассмотренные определения познавательного интереса не противоречат друг другу, взаимно обогащают.
Рассмотрим различные подходы к классификации познавательного интереса, к выделению его уровней.
Интерес к какому-нибудь предмету, к занятию, отрасли знаний, как и внимание, может быть прямым (непосредственным) и косвенным (опосредованным). В случае прямого интереса человека привлекает сам предмет, деятельность определенного вида. Но нередко случается и так, что прямого интереса, например, к математике, ученик не испытывает, но он интересуется физикой и понимает, что без математики в этой области ничего сделать нельзя. В этом случае к математике проявляется косвенный интерес. «Знание учителем непосредственных и косвенных интересов учащихся помогает осуществлению индивидуального подхода» [6, С – 234].
В развитии познавательного интереса можно выделить ряд уровней: любопытство, любознательность, собственно познавательный интерес, творческий интерес. «Эти уровни определяют разную степень избирательной направленности, избирательного отношения ученика к предмету и степень влияния познавательного интереса на личность» [6, С – 235].
Любопытство – элементарная стадия познавательного интереса. Оно обусловлено чисто внешними обстоятельствами, привлекающими внимание человека. Интерес этого уровня – поверхностный, фрагментарный, ситуативный, связанный с переживанием своего отношения к предмету в данный момент. Более высокий уровень познавательного интереса – любознательность. «Для любознательного, при решении задачи, исчезает время и пространство» [6, С – 237]. На этапе любознательности интерес еще в полной мере не освободился от интереса к описаниям, и, тем не менее, он уже носит поисковый характер. При этом импульс активности исходит от самого человека, что в корне меняет характер интереса. Привлекательной для ученика становится сама деятельность. Ученик становится субъектом деятельности. А познавательный интерес с уровня любознательности переходит на более высокий уровень собственно познавательного интереса.
Под творческим интересом понимают такой уровень познавательного интереса, когда ученик стремится осуществить самостоятельную, творческую, поисковую деятельность. Это, в основном, узкий интерес к определенной отрасли знаний.
Л.И. Карташова [15] выделяет следующие уровни развития познавательного интереса: 1) Потребность во впечатлениях. Она ярко выражена у маленьких детей и заключается в реагировании на новизну стимула. 2) Потребность в знаниях. Она выражается в интересе к предмету, склонности к его изучению, любви к чтению книг и так далее. 3) Устойчивые осознанные стремления к получению новых знаний. Познавательная потребность здесь имеет характер целенаправленной деятельности и приводит к общественно значимым результатам.
Выделяют аспекты познавательного интереса:
1) Познавательный интерес как стимул, средство обучения;
2) Познавательный интерес как мотив учебной деятельности;
3) Познавательный интерес как устойчивая черта личности.
Содержание школьного предмета математики таинственно и романтично не для всех учащихся, для многих учащихся математика кажется сухой наукой. Поэтому не следует упускать возможность сделать ее ярче и привлекательней.
«Средство обучения – это материальный или идеальный объект, который «помещен» между учителем и учащимися и использован для усвоения знаний, формирования опыта познавательной и практической деятельности» [12].
Средства обучения оказывают существенное влияние на качество знаний учащихся, их умственное развитие и профессиональное становление.
Средства обучения можно классифицировать по различным основаниям: по их свойствам, субъектам деятельности, влиянию на качество знаний и на развитие различных способностей, их эффективности в учебном процессе.
По субъекту деятельности средства обучения можно условно разделить на средства преподавания и средства учения. Так оборудование демонстрационного эксперимента относится к средствам преподавания, а оборудование лабораторного практикума – к средствам учения.
Средства преподавания помогают возбудить и поддерживать познавательные интересы учащихся, улучшают наглядность учебного материала, делают его более доступным, обеспечивают более точную информацию об изучаемом явлении. Их можно разделить на средства объяснения нового материала, средства закрепления и повторения и средства контроля.
По составу средства обучения разделяются на материальные и идеальные. Материальные средства: учебники и учебные пособия; таблицы, модели, макеты и другие средства наглядности; учебно-технические средства; учебно-лабораторное оборудование; помещения, мебель, микроклимат, расписание занятий, режим питания; другие материально-технические условия обучения.
Идеальные средства обучения – это те усвоенные ранее знания и умения, которые используют учителя и учащиеся для усвоения новых знаний. Л.С. Выгодский [7] приводит такие средства обучения, как речь, письмо, схемы, условные обозначения, чертежи, диаграммы, произведения искусства и другие. В общем случае идеальное средство – это орудие усвоения культурного наследия, новых культурных ценностей.
Система средств обучения строится согласно следующим принципам:
- Оборудование должно полностью удовлетворять педагогическим требованиям, предъявляемым к другим элементам учебного процесса.
- Все приборы, имеющие общее назначение, должны соответствовать друг другу и демонстрационным установкам.
- Количество и типы средств обучения должны полностью обеспечивать материальные потребности учебной программы в системе, но без излишеств.
- Средства обучения должны соответствовать реальным условиям работы и потребностям местного населения.
Таблица классификации средств обучения по различным признакам.
| №
|
Признак
|
Классификация
|
| 1 |
По субъекту деятельности. |
1. Средства преподавания;
2. Средства учения.
|
| 2 |
Средства преподавания. |
1. Средства объяснения нового материала;
2. Средства закрепления;
3. Средства повторения;
4. Средства контроля.
|
| 3 |
По составу. |
1. Материальные средства;
2. Идеальные средства.
|
Использование литературных цитат, подходящих стихов, метафор влияет на развитие познавательного интереса к предмету. Вводя понятие функции, учитель может прочитать, например, стихотворение:
Не было гвоздя –
Подкова пропала.
Не было подковы –
Лошадь захромала.
Лошадь захромала –
Командир убит.
|
Конница разбита-
Армия бежит.
Враг вступает в город,
Пленных не щадя,
Потому что в кузнице
Не было гвоздя.
|
Представление о синусоиде будет богаче, если привести стихи Е.Долматовского: …
Мудрость обретая в трудном споре,
Предначертан путь нелегкий твой
Синусоидой радости и горя,
А не вверх взмывающей кривой.
Шуточные стихи, которые позволяют запомнить различные постоянные, также вызывают интерес учащихся. Например, в старинном стихотворении с буквой «ять» количество букв в каждом слове соответствует цифре в написании числа, что облегчает запоминание цифр числа «Пи»:
«Кто и шутя и скоро пожелаеть,
Пи узнать число, ужъ знаеть» [14, С – 3].
Рассказы об ученых-математиках интересны и поучительны, как и рассказы о происхождении, открытии различных сведений. Материал по истории математики можно найти в работах И.К. Андронова, Г.И. Глейзера, М.Я. Выгодского, Б.Б. Гнеденко, И.Я. Депмана, В.Н. Молодшего, В.Д. Чистякова, Г.Г. Цейтена; в журналах «Математика в школе» и «Квант» и т.д.
Перевод математических терминов на русский язык и рассказы об их происхождении (Дж. Икрамов), также «очеловечивают» школьную математику:
Радиус – спица колеса;
Хорда – тетива лука;
Апофема – нечто, отложенное в сторону и т.д.
В. Шеронова предлагает игры, сказки и жизненные ситуации, которые можно использовать в качестве сюжетов:
1. Разведчик. ««Разведчик, разведчик…», - слышен шепот с первой парты. Ученик у доски замер… Вот же ошибка! При переносе числа из одной части уравнения в другую он забыл сменить знак. Он помнит, что числу («разведчику») надо пересечь границу («=»). Для этого необходимо сменить его форму на чужую, т.е. сменить знак.» [33]. Благодаря этой ассоциации уравнение будто оживает, увлекает.
2. Забывчивый парикмахер. «Парикмахер по рассеянности состриг волосы только с половины вашей головы. Если вы, раскрывая скобки при распределительном законе, забудете умножить каждое из слагаемых, то вы будете очень похожи на этого горе-мастера» [33].
Основным средством развития познавательного интереса являются математические задачи. Решая математическую задачу, человек познает много нового: знакомится с ситуацией, с применением теории к ее решению, познает новые методы решения и т.д.
Решение занимательных, логических задач, не требующих глубокого знания школьного курса математики, также является средством стимулирования познавательного интереса. Существует множество пособий, содержащих занимательные задачи. Среди авторов: И.Я. Перельман, Е.И. Игнатьев, Б.А. Кордемский и многие другие.
В работе К.К. Ким и И.В. Микляева предлагают задачи, которые называют интегрированными. Они показывают связь математики с другими науками, такими как история, литература, биология, информатика и другие. Приведем несколько примеров:
1) «Царь построил своих воинов треугольником, и треугольная фаланга двинулась на врага. Воины в фаланге стояли плотно. Каждый воин занимал место площадью 1,7901 м2
. Основание фаланги составляло 45,9 м; а высота, проведенная к основанию, равнялась 23,4 м. Сколько всего было воинов? Как звали царя? Где произошло сражение, его итоги?» [16].
2) «В литературном произведении описываются события, происходившие на Половецкой земле в году А, в году В для Екатерины II была сделана рукописная копия произведения, а в году С произведение было впервые издано. В году Dрукопись погибла в московском пожаре. О каком произведении идет речь?» [16].
Одним из способов повышения интереса к математике является усиление ее практической направленности. На примере задач прикладного содержания учащиеся будут убеждаться в значении математики для различных сфер деятельности человека, увидят широту возможных приложений, поймут ее роль в современной культуре. Материал по задачам практического содержания можно найти в работах: Н.П. Апанасова и П.Т. Ананасова, С.С. Варданяна, В.А. Петровой, Н.А. Терешина, И.М. Шапиро и других.
«Одним из средств поддержания и развития познавательного интереса на ранних стадиях его становления является игра» [12, С – 252]. Игра содействует активному обучению, нейтрализует перегрузки, способствует разрядке напряженности, создает благоприятную атмосферу учебной деятельности, повышает эффективность процесса обучения. Игра может иметь место на различных этапах урока: в его начале – для концентрации внимания, в середине – для небольшой разрядки, в конце – для повторения. Об играх на уроке можно прочитать в работах: А.А. Окунева, В.Н. Кузнецова, Е.А. Дышинского, Ф.Ф. Нагибина, Е.С. Канина, Т.М. Ковалевой и других методистов.
Действенным приемом стимулирования познавательного интереса является создание в учебном процессе ситуации успеха у школьников, испытывающих определенные затруднения в учебе.
Однако приемы стимулирования познавательного интереса, несмотря на их значимость и разнообразие, действуют ограниченно. С устранением внешней занимательности ситуации, породившей временный интерес, он может быть быстро утрачен. «Приемы «оживления» урока еще не позволяют заглянуть внутрь самого процесса познания, способствовать проявлению устойчивого познавательного интереса» [27, С – 4].
Более действенным, чем средство обучения, познавательный интерес проявляет себя как мотив деятельности. «Там, где идет воздействие на познавательный интерес через сам процесс познания, через деятельность, там познавательный интерес действительно становится мощным средством обучения, а учение приобретает активный, самостоятельный характер» [6, С – 241].
По словам К.Д. Ушинского «приохотить ребенка к учебе гораздо более достойное занятие, чем приневолить». «Меры воздействия на познавательный интерес – не дать ему угаснуть, поддерживать познавательную деятельность на самом высоком из доступных уровней трудности, в «зоне ближайшего развития» такой личности» [6, С – 243]. Это имеет место при выполнении задач повышенной трудности, самостоятельных исследовательских заданий, самостоятельном чтении дополнительной математической литературы, написании докладов, рефератов.
Задача формирования познавательных интересов очень актуальна для построения учебного процесса, так как школе необходимо привить ученику стремление к постоянному пополнению своих знаний с помощью самообразования, содействовать побуждениям расширять свой общий и специальный кругозор.
Активизация познавательной деятельности – побуждение к энергичному, целенаправленному учению (Колмакова М.Н. Краткий педагогический словарь).
Т.И. Шамова выделяет три уровня познавательной активности, определяя их по образу действия: воспроизводящая, интерпретирующая и творческая активность. Находясь на воспроизводящем уровне познавательной активности, учащийся должен научиться воспроизводить полученные знания или умения. На интерпретирующем уровне ученику необходимо научиться интерпретировать или трактовать полученные знания в новых учебных условиях, отталкиваясь от привычных образцов. Творческий уровень познавательной активности характерен для учащихся, которые не только усваивают связи между предметами и явлениями, но и пытаются найти для этой цели новый способ.
Работа учителя по активизации познавательной деятельности учащихся наиболее эффективна, а качество знаний учащихся выше, если при проведении уроков используются приемы и средства, активизирующие познавательную деятельность учащихся и развивающие их познавательный интерес.
Итак, для активизации учащихся в учебном процессе и, следовательно, для развития интереса к предмету можно использовать различные педагогические технологии. Все они предполагают создание условий, способствующих проявлению самостоятельности учащихся при овладении учебным материалом.
Учитель, используя кейс-технологию обучения, систематически целенаправленно развивает у детей подвижность и гибкость мышления, настойчиво стимулирует процессы переключения, поисковую активность; учит детей рассуждать, решать проблемы; самим делать выводы, находить новые оригинальные подходы, получать изящные результаты, красивые решения, чтобы получить удовольствие от учения.
Вывод:
В первой главе проведен анализ таких понятий как «метод», «метод обучения», «проблемные методы», «метод кейсов», «познавательный интерес», «средства обучения» и другие, а также их классификаций, на основе которых составлены таблицы.
В качестве исследования в практической части второй главы выбрана классификация кейсов по уровню сложности и уровню познавательного интереса. А также выделены этапы решения кейс-заданий.
Выполнен анализ программы для образовательных учреждений и учебников по алгебре и началам анализа базового и профильного уровней по теме «Преобразование тригонометрических выражений».
В программе представлены требования к обязательной подготовке учащихся двух уровней – базового и профильного. По теме «Преобразование тригонометрических выражений» на базовом уровне учащиеся должны уметь: 1) находить значения тригонометрических выражений на основе определений с помощью калькулятора или таблиц; 2) выполнять несложные преобразования тригонометрических выражений, применяя ограниченный набор формул, связанных со свойствами тригонометрических функций. На профильном уровне учащиеся должны уметь: 1) находить значения тригонометрических выражений на основе определений с помощью калькулятора или таблиц; 2) выполнять тождественные преобразования тригонометрических выражений [25].
Представленные цели в рамках нашего исследования недостаточны для формирования познавательного интереса. Поэтому были сформулированы следующие цели изучения темы «Преобразование тригонометрических выражений»: 1) научить учащихся распознавать, анализировать, разрешать проблемную ситуацию, выдвигать гипотезу, анализировать полученный результат; 2) формировать умения решения кейс-заданий на применение преобразований тригонометрических выражений; 3) развивать познавательный интерес к предмету через кейс-задания.
Анализ действующих учебников по алгебре и началам анализа под редакцией А.Г. Мордковича, базового и профильного уровней, на наличие заданий, содержащих проблему и направленных на формирование и повышение познавательного интереса.
В учебниках базового уровня по теме «Преобразование тригонометрических выражений» предложено 181 задание, из них 20 заданий направлены на формирование познавательного интереса. В учебниках профильного уровня по этой же теме предложено 326 заданий, из них 100 заданий направлены на формирование познавательного интереса.
учебник
параметр
|
А.Г. Мордкович «Алгебра и начала анализа», 10 класс (базовый уровень) |
А.Г. Мордкович «Алгебра и начала математического анализа», 10 класс (профильный уровень) |
| Общее количество заданий |
181 |
326 |
| Задания, на развитие познавательного интереса |
20 |
100 |
| Процент заданий, направленных на развитие познавательного интереса |
11 % |
31 % |
Вывод:
Представленные в учебниках задания не содержат явной проблемы, но при соответствующей доработке могут стать проблемными или кейсовыми.
§2. Система кейс-заданий по теме
«Преобразование тригонометрических выражений», направленная на формирование познавательного интереса.
Классификация кейсов может производиться по различным признакам. Для нашего исследования мы выбрали классификацию по уровню сложности и уровню познавательного интереса.
Классификация кейсов, направленная на формирование познавательного интереса учащихся:
- Учебные иллюстративные кейсы, соответствующие
I
уровню познавательного интереса – любопытству и формирующие умения выделять основную проблему.
Цель кейс-заданий – формирование у учащихся любопытства при решении практических примеров, в которых они должны выделить основную проблему.
Последовательность действий.
1) Учитель предлагает практический пример, 2) создает ситуации, 3) анализирует их вместе с детьми. 4) Учащиеся следят за ходом мыслей учителя, 5) выдвигают гипотезы по определению возможных проблем, 6) выделяют основную проблему. 7) Дети вместе с учителем находят пути решения, 8) выбирают оптимальный путь и 9) решают проблему.
- Учебные кейсы с формулированием проблемы, соответствующие
II
уровню познавательного интереса – любознательности и формирующие умения анализировать ситуацию, формулировать проблему при решении кейс-заданий.
Цель кейс-заданий – формирование у учащихся любознательности при проведении диагностики ситуации.
Последовательность действий.
1) Учитель создает ситуацию. 2) Учащиеся анализируют ситуацию, 3) выдвигают гипотезы по определению возможных проблем, 4) выделяют основную проблему. 5) Дети вместе с учителем находят пути решения, 7) выбирают оптимальный путь и 8) решают проблему.
- Прикладные кейсы, соответствующие
III
уровню познавательного интереса – собственно познавательному интересу и формирующие умения находить и предлагать концепцию решений.
Цель кейс-заданий – формирование собственно познавательного интереса при поиске путей решения проблемы.
Последовательность действий.
1) Учитель создает ситуацию. 2) Учащиеся анализируют ситуацию, 3) выдвигают гипотезы по определению возможных проблем, 4) выделяют основную проблему, 5) предлагают возможные пути решения, 7) выбирают оптимальный путь. 8) Учитель вместе с детьми решает проблему.
- Учебные кейсы без формулирования проблемы, соответствующие
IV
уровню познавательного интереса – творческому интересу и формирующие умения видеть ситуацию, формулировать проблему и решать ситуацию.
Цель кейс-заданий – формирование творческого интереса при самостоятельном разрешении ситуации.
Последовательность действий.
1) Учитель создает ситуацию. 2) Учащиеся анализируют ситуацию, 3) выдвигают гипотезы по определению возможных проблем, 4) выделяют основную проблему, 5) предлагают возможные пути решения, 7) выбирают оптимальный путь, 8) решают проблему.
Кейс-задания.
Тема «Формулы понижения степени».
1. Дан корень уравнения 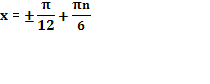 . .
Учитель задает вопрос: «Что мы можем с ним сделать?»
Варианты ответов: исследовать, найти исходное уравнение и другие.
2. Дан корень уравнения . .
3. Дан корень уравнения 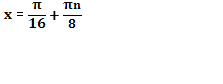 . .
4. Дано выражение  . .
Учитель задает вопрос: «Как можно представить  ?» ?»
Варианты ответов: по формуле двойного аргумента 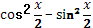 , как функцию , как функцию  и другие. и другие.
Тема «Формулы двойного аргумента».
5. 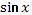 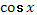  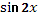
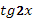 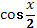  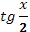 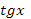
Учащимся предлагаются тригонометрические функции с разными аргументами. Учитель задает вопрос: «Что мы можем с ними сделать?».
Варианты ответов: классифицировать по названию функции, по аргументу и другие.
6. Даны корни уравнения и .
Учитель задает вопрос: «Что мы можем с ним сделать?»
Варианты ответов: исследовать, найти исходное уравнение и другие.
7. Даны корни уравнения  и . и .
8. Даны корни уравнения  и и  . .
Тема «Преобразование суммы тригонометрических функций в произведение».
9. Даны выражения 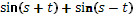
 . .
Учитель задает вопрос: «К чему приведут эти выражения?»
Варианты ответов: к выводу формул, к упрощению выражений и другие.
10. Дано выражение  . Поставьте вопрос. . Поставьте вопрос.
Варианты ответов: представить разность в виде произведения, решить уравнение и другие.
11. Дано выражение  . .
Учитель задает вопрос: «Что можно сделать с этим выражением?».
Варианты ответов: представить сумму в виде произведения, решить уравнение, упростить выражение и другие.
Тема «Преобразование произведения тригонометрических функций в сумму».
12. Сначала сравнивается название темы с предыдущей, и находятся общие черты и различия. Затем учащимся предлагается рассмотреть ранее изученные формулы: 1)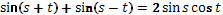 . .
2) . .
3) . .
Учитель задает вопрос: «Какую задачу мы поставим перед собой?».
Варианты ответов: доказать тождество, выразить формулы и другие.
13. Дано равенство .
Учитель задает вопрос: «Какую задачу можно поставить?».
Варианты ответов: решить уравнение, доказать тождество и другие.
14. Дано равенство .
15. Дано выражение  . Сформулируйте и запишите задание и решите его. . Сформулируйте и запишите задание и решите его.
Тема «Преобразование тригонометрических выражений».
16. Дано, что  , ,  и и  . .
Учитель задает вопрос: «Что нужно сделать?».
Варианты ответов: найти значение выражения, решить уравнение и другие.
17. 1) 
2) 
3) 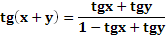
4) 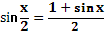
5) 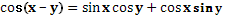
6) 
7) 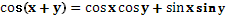
8) 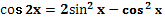
9) 
10) 
11) 
12)  . .
Учитель задает вопрос: «Что вы видите? Что нужно с ними сделать?».
Варианты ответов: формулы, выражения и другие; классифицировать, найти ошибки и другие.
Вывод:
Задания под № 4, 5, 9, 12 можно использовать на этапе изучения нового материала, они формируют познавательный интерес I уровня. Задания под № 1, 6, 10, 11, 13, 14, 15, 16 можно использовать на этапе закрепления, они формируют познавательный интерес II уровня. Задания под № 1, 6, 11, 13, 17 можно использовать на этапе актуализации знаний, они формируют познавательный интерес III уровня. Задания под № 2, 3, 7, 8 можно использовать на этапе самостоятельной работы, они формируют познавательный интерес IV уровня.
| № |
Тема |
Цели |
Кейс-задания |
| 1 |
Формулы двойного аргумента. |
Познакомить учащихся с формулами двойного аргумента. Научить учащихся алгоритму принятия правильного решения в определенной ситуации. Определить уровень сформированности познавательного интереса к предмету. |
Задание № 1
Кейс-задания
|
| 2 |
Отработать навыки применения формул двойного аргумента при решении заданий. Научить учащихся диагностировать ситуации и самостоятельно принимать решения по указанной проблеме. Развивать познавательный интерес к предмету. |
Задание № 2, 3
Кейс-задания
|
| 3 |
Формулы понижения степени. |
Познакомить учащихся с формулами понижения степени. Научить учащихся алгоритму принятия правильного решения в определенной ситуации. Развивать познавательный интерес к предмету. |
Задание № 4
Кейс-задания
|
| 4 |
Отработать навыки применения формул понижения степени при решении заданий. Научить учащихся ставить и видеть проблему, выдвигать гипотезы по ее решению. Развивать познавательный интерес к предмету. |
Задание № 5, 6
Кейс-задания
|
| 5 |
Преобразование суммы тригонометрических функций в произведение. |
Познакомить учащихся с формулами преобразования суммы тригонометрических функций в произведение. Научить учащихся диагностировать ситуацию и самостоятельно принимать решения по указанной проблеме. Развивать познавательный интерес к предмету. |
Задание № 7, 8
Кейс-задания
|
| 6 |
Отработать навыки применения формул преобразования суммы тригонометрических функций в произведение при решении заданий. Научить учащихся самостоятельно выявлять проблему, указывать альтернативные пути ее решения с анализом наличных ресурсов, решать проблему. Развивать познавательный интерес к предмету. |
Задание № 9
Кейс-задания
|
| 7 |
Преобразование произведения тригонометрических функций в сумму. |
Познакомить учащихся с формулами преобразования произведения тригонометрических функций в сумму. Научить учащихся диагностировать ситуации и самостоятельно принимать решения по указанной проблеме. Развивать познавательный интерес к предмету. |
Задание № 10
Кейс-задания
|
| 8 |
Отработать навыки применения формул преобразования произведения тригонометрических функций в сумму при решении заданий. Научить учащихся самостоятельно выявлять проблему, указывать альтернативные пути ее решения с анализом наличных ресурсов, решать проблему. Развивать познавательный интерес к предмету. |
Задание № 11
Кейс-задания
|
| 9 |
Преобразование тригонометрических выражений. |
Отработать навыки применения формул преобразования тригонометрических выражений при решении заданий. Научить учащихся самостоятельно выявлять проблему, указывать альтернативные пути ее решения с анализом наличных ресурсов, решать проблему. Развивать познавательный интерес к предмету. |
Задание № 12
Кейс-задания
|
| 10 |
Контрольная работа |
Определение уровня знаний, умений, навыков по теме «Преобразование тригонометрических выражений», определение уровня сформированности познавательного интереса учащихся. |
Задание № 13
Итоговый контроль
|
В настоящее время все чаще используют инновационные технологии образования. Одним из вариантов является кейс-технология. Причем, ее использование возможно в сочетании с другими образовательными технологиями.
На основе проведенного исследования А. Долгоруким были выделены следующие этапы применения кейс-технологии на уроках математики: 1) подготовка и предоставление учителем учебно-методического материала по изучаемой теме каждому ученику; 2) планомерная и последовательная работа с учащимися по проработке каждого вопроса темы, предполагающая как самостоятельное изучение ребенком отдельных вопросов, так и работу в классе или индивидуальные консультации; 3) обязательное обобщение изучаемой темы учителем, выявление пробелов в изучении отдельных вопросов темы и их устранение; 4) диагностика по окончании изучения темы или раздела.
В соответствии с тематическим планированием составлено 13 фрагментов уроков по теме «Преобразование тригонометрических выражений», которые были реализованы в урочное время. 4 фрагмента по изучению нового материала, 4 – на закрепление, 1 – на актуализацию знаний, 4 – самостоятельных и контрольных работ.
На этапе контроля знаний проверяются уровни сформированности познавательного интереса с помощью умений решать кейсы, на этапах изучения нового материала, актуализации знаний и закреплении формируются уровни познавательного интереса и уровни умений решать кейсы.
Были разработаны следующие методические схемы применения кейс метода, направленные на формирование познавательного интереса.
- Методическая схема решения кейс-заданий 1 уровня.
| Деятельность учителя
|
Деятельность учащихся
|
1. Предлагает практический пример.
2. Создает ситуацию.
3. Предлагает систему вопросов для анализа ситуации.
4. Подводит учащихся к формулированию проблем.
5. Следит за отбором проблем.
6. Руководит поиском решения проблемы.
7. Решает ситуацию.
|
1. Рассматривают пример.
2. Внимательно слушают.
3. Анализируют ситуацию.
4. Выдвигают гипотезы по определению возможных проблем.
5. Выделяют основную проблему.
6. Находят пути решения проблемы.
7. Решают ситуацию.
|
Фрагмент урока №1 по теме «Формулы двойного аргумента» (25.11.2009г).
Тип урока: изучение нового материала.
Цели:
образовательные
: изучить формулы двойного аргумента и отработать умения по их применению;
воспитательные
: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: изучение нового материала.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
- Перейдем к изучению нового материала. Откройте тетради, запишите число и тему урока «Формулы двойного аргумента».
(
предлагает практический пример и создает ситуацию
)
- На доске записаны тригонометрические функции.
(предлагает систему вопросов для анализа ситуации)
- Что можно с ними сделать?
- По каким признакам мы можем их классифицировать?
- Что у нас получится?
- Еще?
- Что получится?
(подводит учащихся к формулированию проблем)
- Какие аргументы у нас получились в каждом столбике?
- Обратите внимание на последний столбик.
- Как вы думаете, что нам нужно сделать с этими выражениями?
(анализ данных)
- Рассмотрим выражение 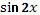 . .
- Как называется в данном выражении?
(выдвижение гипотез)
- Как мы можем представить ?
- Как дальше можем преобразовать?
- Правильно.
(решение проблемы)
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Перепишите еще раз начало и конец, и обведите в рамочку.
(анализ полученных результатов)
- Таким образом, что мы получили?
- Аналогично выводится формула для 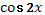 . .
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Запишите формулу и обведите в рамочку.
(анализ данных)
- В виде чего представлена данная формула?
(выдвижение гипотез)
- Можно ли представить формулу так, чтобы она содержала в правой части только синус?
- Как?
- Что получится? Диктуйте. (решение проблемы)
- Запишите формулу и обведите в рамочку.
- Можно ли представить формулу так, чтобы она содержала в правой части только косинус?
- Как?
- Запишите каждый у себя в тетрадях. А Лашкевич Ольга запишет на доске.
- Молодец. Садись.
- Запишите формулу и обведите в рамочку.
- А для  выведет формулу …..? выведет формулу …..?
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Перепишите еще раз начало и конец, и обведите в рамочку.
- Таким образом, мы с вами вывели три формулы двойного аргумента.
- Скажите, пожалуйста, для каких значений аргумента справедливы формулы синуса двойного аргумента и косинуса двойного аргумента?
- Правильно. А для каких значений аргумента справедлива формула тангенса двойного аргумента?
- Какое здесь еще существует необходимое условие?
- Данные формулы можно применять как справа налево, так и слева направо.
- Разумеется, формулы двойного аргумента можно применять и в тех случаях, когда место аргумента 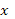 занимает более сложное выражение. занимает более сложное выражение.
- Может, вы скажете сразу, без вычислений, чему равен  ? ?
- Правильно. Молодцы.
|
(рассматривают пример)
(анализируют ситуацию)
- Классифицировать.
- По названию функций.
Дети классифицируют.
- По аргументу.
Дети классифицируют.
(выдвигают гипотезы по определению возможных проблем)
- В первом столбике – единичный аргумент, во втором – половинный, в третьем – двойной.
- Вывести формулы.
(анализируют данные)
- Аргументом.
(выдвигают гипотезу)
- Как  . .
- По формуле синуса суммы.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
-  . .

- Мы вывели формулу двойного аргумента для синуса.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
-  . .
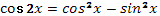
(анализируют данные)
- В виде двух тригонометрических функций.
(выдвигают гипотезу)
- Да.
- Выразить 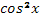 по основному тригонометрическому тождеству. по основному тригонометрическому тождеству.
- 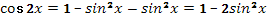 . .
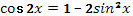
- Да.
- Тоже по тригонометрическому тождеству.
Лашкевич Ольга выходит к доске и записывает:
- 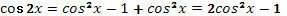 . .
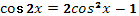
Один ученик выходит к доске. Остальные выполняют в тетрадях.
-
 . .

- Для любых значений аргумента.
- Для тех значений аргумента  , для которых определены , для которых определены  и и  . .
- Знаменатель должен быть не равен нулю.
-  . .
|
Задание № 1.
 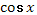
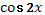 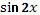
 
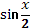 
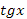
 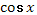 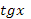
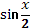  
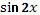 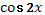 
 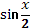 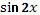
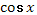  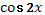
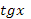  
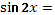

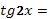
 . .

 . .
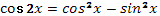
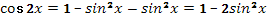 . .
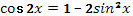
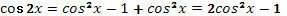 . .
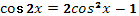
 . .

 . .
|
- Методическая схема решения кейс-заданий 2 уровня.
| Деятельность учителя
|
Деятельность учащихся
|
1. Создает ситуацию.
2. Подводит учащихся к формулированию проблем.
3. Руководит отбором проблем.
4. Руководит поиском решения проблемы.
5. Решает ситуацию.
|
1. Внимательно слушают, анализируют ситуацию.
2. Выдвигают гипотезы по определению возможных проблем.
3. Выделяют основную проблему.
4. Находят пути решения.
5. Решают ситуацию.
|
Фрагмент урока №2 по теме «Формулы двойного аргумента» (25.11.2009г).
Тип урока: закрепление.
Цели:
образовательные
: отработать умения по применению формул двойного аргумента;
воспитательные
: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: закрепление.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(создает ситуацию)
- Даны корни уравнения 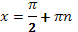 и и  . .
(подводит учащихся к формулированию проблем)
- Что мы можем с ними сделать?
- Каким должно быть уравнение?
- А еще каким?
(анализ данных)
- Какое это будет уравнение, простейшее или сложное?
- А как вы определили, что оно сложное?
(выдвижение гипотез)
- В каком случае можно приравнять уравнения?
(поиск путей решения и решение проблемы)
- Какое мы можем составить первоначальное уравнение?
- Мы можем оставить такое уравнение?
- Дальше что нужно?
- Мы можем ее применить?
- Почему?
- Что получится?
- Что получим?
- Подобное задание будет в самостоятельной работе.
|
(выдвигают гипотезы по определению возможных проблем и выделяют основную проблему)
- Найти уравнение, которому принадлежат эти корни.
- Тригонометрическим.
- На тему урока.
(анализируют данные)
- Сложное.
- Будет состоять из двух простейших.
- Первому корню соответствует уравнение 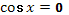 . Второму – . Второму – 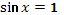 . .
(выдвигают гипотезу)
- Когда оба уравнения равны нулю.
-  . .
- 
- 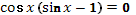 . .
- Да, но можем раскрыть скобки.
- 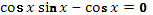
- Так как уравнение должно быть на тему урока, то нужно применить формулу двойного аргумента.
- Нет.
- Можно было применить, если бы перед  стояла двойка. стояла двойка.
- Нужно домножить обе части уравнения на 2.
- . Отсюда, свернув по формуле синуса двойного аргумента, получим
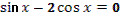 . .
|
Задание № 2.
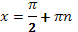

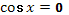 . .
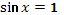 . .
 . .
 . .
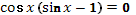 . .
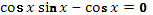 . .
.
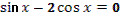 . .
|
- Методическая схема решения кейс-заданий 3 уровня.
| Деятельность учителя
|
Деятельность учащихся
|
1. Создает ситуацию.
2. Подводит учащихся к формулированию проблем.
3. Руководит отбором проблем.
4. Следит за правильностью рассуждений.
5. Подводит учащихся к выбору оптимального пути решения.
6. Решает ситуацию.
|
1. Внимательно слушают, анализируют ситуацию.
2. Выдвигают гипотезы по определению возможных проблем.
3. Выделяют основную проблему.
4. Предлагают концепцию решений.
5. Выбирают из всевозможных предложений оптимальный путь решения.
6. Решают ситуацию.
|
Фрагмент урока №5 по теме «Преобразование суммы тригонометрических функций в произведение» (02.12.2009г).
Тип урока: изучение нового материала.
Цели:
образовательные
: повторить ранее изученный материал;
воспитательные
: воспитать внимание, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, находить оптимальные пути решения проблемы, формирование познавательного интереса к математике.
Этап урока: актуализация знаний.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
- Поработаем устно.
(создает ситуацию, подводит учащихся к формулированию проблем)
- Что вы видите на доске?
- А еще?
- Что это за формулы?
- Как вы думаете, зачем они записаны на доске?
- У кого есть другие варианты?
- Какую задачу мы поставим перед собой?
(решение проблемы)
- Есть ли в первой формуле ошибки?
- Правильно. А во второй формуле?
- Правильно. В третьей формуле?
- В четвертой?
- А в пятой?
- Правильно. В шестой формуле?
- Есть ли ошибка в седьмой формуле?
- В восьмой формуле?
- В девятой?
- В десятой?
- В одиннадцатой формуле?
- И в последней формуле?
- Молодцы!
|
(выдвигают гипотезы по определению возможных проблем и выделяют основную проблему)
- Равенства.
- Формулы.
- Преобразования тригонометрических выражений.
- Чтобы вспомнить, и легче было решать задания.
- В них допущены ошибки.
- Необходимо найти ошибки.
(поиск путей решения и решение проблемы)
- В первой формуле в правой части надо поменять знак на «+» и поменять функции 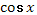 и и  местами. местами.
- Во второй формуле между функциями  и и 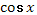 должен стоять знак « должен стоять знак « ». ».
- В третьей формуле в знаменателе между 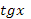 и и  стоит знак умножения. стоит знак умножения.
- В четвертой формуле в числителе вместо знака «+» надо поставить знак «-» и поменять  на на 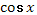 . .
- В пятой формуле надо поменять функции и и 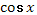 местами. местами.
- В шестой формуле надо поменять числитель и знаменатель местами.
- В седьмой формуле надо в правой части поменять знак на «-».
- В восьмой формуле в правой части нет двойки и надо поменять  и и 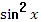 местами. местами.
- В девятой формуле все верно.
- В десятой формуле тоже все верно.
- В одиннадцатой формуле в числителе между 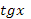 и и  стоит знак «-», а в знаменателе после 1 стоит знак «+». стоит знак «-», а в знаменателе после 1 стоит знак «+».
- В двенадцатой формуле в числителе должно быть .
|
Задание № 7.

2) 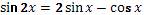
3) 
4) 
5) 
6) 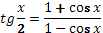
7) 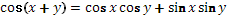
8) 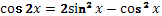
9) 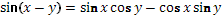
10) 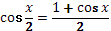
11) 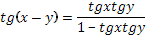
12) 
|
- Методическая схема решения кейс-заданий 4 уровня.
| Деятельность учителя
|
Деятельность учащихся
|
1. Создает ситуацию.
2. Подводит учащихся к формулированию проблем.
3. Руководит отбором проблем.
4. Следит за правильностью рассуждений.
5. Подводит учащихся к выбору оптимального пути решения.
6. Следит за процессом решения.
|
1. Внимательно слушают, анализируют ситуацию.
2. Выдвигают гипотезы по определению возможных проблем.
3. Выделяют основную проблему.
4. Предлагают концепцию решений.
5. Выбирают из всевозможных предложений оптимальный путь решения.
6. Решают ситуацию.
|
Фрагмент урока №8 по теме «Преобразование произведения тригонометрических функций в сумму» (14.12.2009г).
Тип урока: закрепление.
Цели:
образовательные
: закрепить формулы преобразования произведения тригонометрических функций в сумму и отработать умения по их применению;
воспитательные
: воспитать внимание, умение работать самостоятельно;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, находить оптимальные пути решения, решать проблему, формирование познавательного интереса к математике.
Этап урока: самостоятельная работа.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(
создает ситуацию
)
- А сейчас самостоятельная работа. Подпишите листочки и номер варианта. Я раздам вам карточки. Каждая карточка содержит по 4 задания. Первые три задания общего характера. Четвертое задание творческого характера на отдельную оценку. В первом задании необходимо представить выражение в виде суммы, во втором – вычислить, в третьем – решить уравнение. В четвертом задании – дано выражение. Ваша задача сформулировать задание и решить его. Время для работы 20 минут. Критерии оценивания: 3 правильно решенных задания на «5», 3 задания с недочетами - «4», 2 задания на «3» и соответственно меньше двух заданий «2». Время пошло. Приступаем к выполнению заданий.
|
(рассматривают пример, анализируют ситуацию, выдвигают гипотезы по определению возможных проблем и выделяют основную проблему, находят пути решения и решают ситуацию)
|
Задание № 11.
Дано выражение
 . .
Сформулируйте задание и решите.
|
Данное кейс-задание учащиеся выполняют самостоятельно.
В самостоятельной работе первые три задания общего характера, 4 задание – на формирование I, II, III и IV уровней познавательного интереса.
Самостоятельная работа.
Вариант 1.
1.
Представьте в виде суммы:
 . .
2.
Вычислите:
 . .
3.
Решите уравнение:
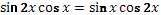 . .
4*
.
Дано выражение
 . .
Сформулируйте задание и решите.
|
Самостоятельная работа.
Вариант 2.
1.
Представьте в виде суммы:
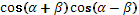 . .
2.
Вычислите:
 . .
3.
Решите уравнение:
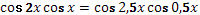 . .
4*
.
Дано выражение
 . .
Сформулируйте задание и решите.
|
Общие критерии оценивания первых трех заданий:
«5» - верно выполненные 3 задания.
«4» - 3 задания с недочетами.
«3» - 2 задания.
«2» - менее 2 заданий.
Критерии оценивания кейс-задания:
1. Правильно сформулировано задание.
2. Правильно выполнены преобразования.
3. Применение формул преобразования тригонометрических выражений.
4. Найдено уравнение.
«2» - менее 2 пунктов (I уровень).
«3» - 2 пункта (II уровень).
«4» - 3 пункта (III уровень).
«5» - 4 пункта (IV уровень).
Вывод:
Во второй главе выделены цели изучения темы «Преобразования тригонометрических выражений», классификация кейс-заданий, формирующая умения решать кейсы и уровни познавательного интереса. Составлено тематическое планирование. Разработана система заданий и методика работы над ними.
Цель эксперимента –
установить степень повышения познавательного интереса учащихся к математике под воздействием кейс-технологии.
Задачи:
1) Выявить уровень сформированности познавательного интереса до экспериментального обучения;
2) Разработать контрольные задания и способы оценивания уровня познавательного интереса;
3) Провести экспериментальное обучение с применением кейс-технологии;
4) Выявить уровень сформированности познавательного интереса после экспериментального обучения;
5) Проанализировать влияние экспериментального обучения на формирование познавательного интереса.
Объект
– деятельность учащихся, направленная на формирование познавательного интереса.
Предмет
– характер воздействия кейс-технологии на повышение познавательного интереса.
Гипотеза
– применение метода кейсов будет способствовать повышению уровня познавательного интереса учащихся по сравнению с традиционными методами обучения.
Методы эксперимента:
метод сбора и накопления данных (анкетирование, интервью, наблюдение); статистические методы (количественная и качественная обработка материалов методами математической статистики, сравнение, шкалирование); методы конструирования явлений (создание определенных педагогических и психологических ситуаций, экспериментальное обучение).
Эксперимент проводился в период с 16.11.2009 г. по 19.12.2009 г. в МОСШ № 32 в 10А
классе и включал четыре этапа: констатирующий, диагностирующий до эксперимента, формирующий, диагностирующий после эксперимента. С программой экспериментального исследования можно ознакомиться в Приложении 8.
Цель этапа: разработать методику формирования познавательного интереса на уроках математики с помощью кейс-технологии, систему заданий, анкеты.
Для достижения поставленной цели были разработаны анкеты для учащихся, система вопросов для интервью с учителем, система заданий, методика формирования познавательного интереса на уроках математики с помощью кейс-технологии.
Также проведено наблюдение за деятельностью учителя на уроках математики с целью выявления применения методов проблемного изложения, кейс-технологии и способов активизации познавательного интереса. Было посещено 7 уроков. Наблюдение показало, что обеспечению познавательной активности учащихся на уроках математики способствовали методы проблемного изложения материала, используемые Одобеско Ниной Михайловной. Использование таких методов осуществлялось на этапах изучения нового материала, актуализации знаний, закрепления. О кейс-технологии учитель ничего не слышала и узнала о ней в процессе наблюдения за экспериментальным обучением.
Цель этапа: провести диагностику умений находить, создавать и решать проблемные ситуации, направленные на формирование познавательного интереса, установить уровень сформированности познавательного интереса к математике до эксперимента.
Для достижения поставленной цели было проведено интервью с учителем, анкетирование учащихся, вводный контроль по теме «Преобразование тригонометрических выражений».
- Интервью с учителем математики Одобеско Ниной Михайловной.
Цель интервью: определить отношение учителя к кейс-методу обучения, определить через какие методы, формы, средства учитель формирует познавательный интерес к математике.
Вопросы интервью:
1. Сколько лет Вы преподаете в школе? Ваш стаж работы?
2. Над какой проблемой работает школа?
3. Над какой проблемой работаете Вы?
4. Какие формы уроков преобладают?
5. Какие методы преобладают на уроках?
6. Какие подходы к ученикам у Вас преобладают?
7. Используете ли Вы проблемное обучение или его элементы на уроках?
8. На каких этапах урока преобладает проблемное обучение?
9. Какие проблемные методы Вы используете?
10. Как Вы развиваете интерес?
11. Знакомы ли Вы с кейс-технологией?
12. Часто ли Вы даете задания для самостоятельного изучения?
13. Даете ли Вы на уроках индивидуальные задания? Как часто?
14. Часто ли Вы на уроках математики решаете сюжетные задачи?
15. Даете ли Вы творческие задания? Как часто?
16. Даете ли Вы на уроках такие задания, когда есть вопрос, но нет условия и ученикам необходимо его составить?
17. Даете ли Вы задания, когда есть условие, но нет вопроса и ученикам необходимо его поставить?
Учитель не обладает достаточной информацией относительно метода кейсов. В своей педагогической деятельности с целью развития познавательного интереса использует проблемные, поисковые или частично-поисковые методы. Использование таких методов происходит на этапе изучения нового материала. По мнению учителя, метод кейсов способствует формированию познавательного интереса к математике, но такой цели – формирование познавательного интереса учащихся с помощью метода кейсов, на уроках не ставится.
- Вводное анкетирование учащихся.
Цель анкетирования: определить, знакомы ли учащиеся с таким методом обучения, как метод кейсов, заинтересованы ли они в обучении математике, выявить уровни сформированности познавательного интереса.
Вводное анкетирование состоит из 17 вопросов (открытые, с вариантами ответов). С анкетами учащихся можно ознакомиться в Приложении 9, с анализом анкет – в Приложении 10. По результатам анкетирования были сделаны следующие выводы:
- 74% учащихся относятся к математике положительно, 26% - нейтрально;
- 39% учащихся хотели бы изучать математику углубленно, 31% ответили отрицательно, 26% не дают однозначного ответа;
- 83% учащихся считают математику интересным предметом, 35% из которых изучают данный предмет с целью удовлетворения своего интереса.
- На вопросы о проблемном обучении большинство учащихся ответили положительно.
Таким образом, можем сделать вывод, что учащиеся имеют представление о проблемных методах обучения. Они заинтересованы в математике, и большинство изучают ее с целью успешной сдачи ЕГЭ и поступления в ВУЗ.
- Вводный контроль.
Контроль № 1.
Цель – установить уровень сформированности познавательного интереса учащихся.
Работа состояла из 4 заданий разного уровня сложности. 1 задание – I уровень, 2 задания – I и II уровни, 3 задания – I, II и III уровни, 4 задания – I, II, IIIи IV уровни познавательного интереса.
Самостоятельная работа №1.
Вариант 1.
1.
Упростить выражение:
 . .
2.
Вычислить:
 . .
3.
Решите уравнения:
а)
 ; ;
б)
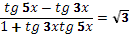 . .
4.
Доказать тождество:
 . .
|
Самостоятельная работа №1.
Вариант 2.
1.
Упростить выражение:
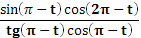 . .
2.
Вычислить:
 . .
3.
Решите уравнения:
а)
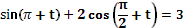 ; ;
б)
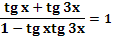 . .
4.
Доказать тождество:
 . .
|
Критерии оценивания:
«5» - 4 задания (IVуровень).
«4» - 3 задания (III уровень).
«3» - 2 задания (II уровень).
«2» - менее 2 заданий (I уровень).
Если ученик выполнил хотя бы одно задание, это говорит о том, что у него сформирован начальный уровень познавательного интереса – любопытство, 2 задания – любознательность, 3 задания – собственно познавательный интерес, 4 задания – творческий интерес.
Выполнена статистическая обработка материала. Проведен анализ по следующим признакам: отметка, уровень сформированности познавательного интереса и составлен вариативный ряд (Приложение 11).
| Оценка |
"2" |
"3" |
"4" |
"5" |
| Количество учащихся |
7 |
10 |
6 |
3 |
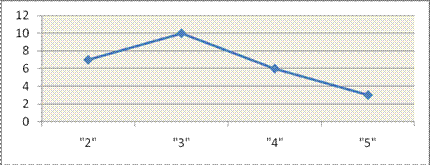
| Уровень |
I уровень |
II уровень |
III уровень |
IV уровень |
| Количество учащихся |
7 |
10 |
6 |
3 |
| 27% |
38% |
23% |
11% |

Таким образом, 27% учащихся имеют I уровень сформированности познавательного интереса, 38% - Iи IIуровни, 23% - I, IIи III уровни и 11% - I, II, III и IV уровни. Учащиеся испытывают трудности при решении заданий на применение формул приведения, практически никто из учащихся не приступил к решению 4 задания.
Цель этапа: развитие познавательного интереса с помощью умений решать кейс-задания.
Для достижения поставленной цели было проведено, в соответствии с тематическим планированием, 10 уроков по теме «Преобразование тригонометрических выражений».
Проведен промежуточный контроль.
Фрагмент урока №4 по теме «Формулы понижения степени» (30.11.2009г).
Тип урока: закрепление.
Цели:
образовательные
: закрепить умения применять формулы понижения степени;
воспитательные
: воспитать внимание, умение самостоятельно находить пути решения и решать ситуацию;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, находить оптимальные пути решения, решать проблему, формирование познавательного интереса к математике.
Этап урока: самостоятельная работа.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(
создает ситуацию
)
- На листочках подпишите фамилию, имя, «Самостоятельная работа» и номер варианта. Я раздала вам карточки. Каждая карточка содержит по 4 задания. В первом задании необходимо решить уравнение, во втором – доказать тождество, в третьем – вычислить. В четвертом задании дан корень уравнения, вам необходимо найти выход из ситуации. Это задание со звездочкой на отдельную оценку. Время для работы 20 минут. Критерии оценивания: 3 задания на «5», 2 задания - «4», 2 задания с недочетами на «3» и соответственно одно задание и меньше «2». Время пошло. Приступаем к выполнению заданий.
|
(рассматривают пример, анализируют ситуацию, выдвигают гипотезы по определению возможных проблем и выделяют основную проблему, находят пути решения и решают ситуацию)
|
Задание № 6.
1 вариант.
Дан корень уравнения
 . .
2 вариант.
Дан корень уравнения  . .
|
Контроль № 2.
Самостоятельная работа №2.
Вариант 1.
1.
Решите уравнение:
 . .
2.
Докажите тождество:
.
3.
Известно, что  .Вычислите .Вычислите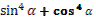 . .
4*.
Дан корень уравнения
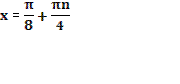 . .
|
Самостоятельная работа №2.
Вариант 2.
1.
Решите уравнение:
.
2.
Докажите тождество:
.
3.
Известно, что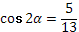 . Вычислите . Вычислите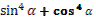 . .
4*.
Дан корень уравнения
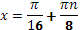 . .
|
В самостоятельной работе первые три задания общего характера, 4 задание, содержащее кейс – на формирование I, II, III и IV уровней познавательного интереса.
Общие критерии оценивания первых трех заданий:
«5» - верно выполненные 3 задания.
«4» - 3 задания с недочетами.
«3» - 2 задания.
«2» - менее 2 заданий.
Критерии оценивания кейс-задания:
1. Верно определена проблема.
2. Правильно выполнены преобразования.
3. Применение формул преобразования тригонометрических выражений.
4. Найдено уравнение.
«5» - 4 пункта (IV уровень).
«4» - 3 пункта (III уровень).
«3» - 2 пункта (II уровень).
«2» - 1 пункт и менее (I уровень).
Выполнена статистическая обработка материала. Проведен анализ по следующим признакам: отметка, уровень сформированности познавательного интереса с помощью умений решать кейс-задания и составлен вариативный ряд (Приложение 12).
| Оценка |
"2" |
"3" |
"4" |
"5" |
| Количество учащихся |
0 |
1 |
9 |
4 |

| Уровень |
I уровень |
II уровень |
III уровень |
IV уровень |
| Количество учащихся |
0 |
1 |
9 |
4 |
| 0% |
7% |
64% |
29% |
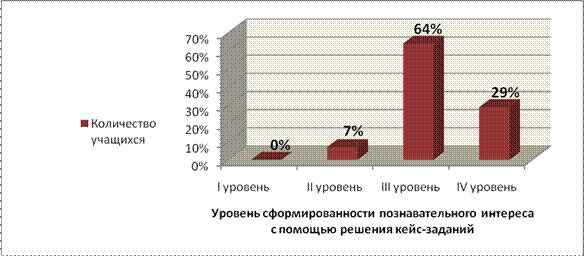
Можем сделать вывод, что уровень сформированности познавательного интереса стал выше благодаря решению кейс-заданий. 0% означает, что у всех учащихся сформирован I уровень познавательного интереса, 7% учащихся имеют I и II уровни, 64% учащихся имеют I, II и IIIуровни, 29% учащихся имеют I, II, III и IV уровни сформированности умений решать кейсы, которые соответствуют такому же уровню сформированности познавательного интереса.
Учащиеся научились анализировать данные, выдвигать гипотезы по определению основной проблемы и решать ситуации, а также анализировать полученные результаты.
Цель этапа: установить уровень сформированности познавательного интереса учащихся после проведения экспериментального обучения.
Для достижения поставленной цели было проведено итоговое анкетирование учащихся, итоговая контрольная работа по теме «Преобразование тригонометрических выражений».
- Итоговый контроль.
Была проведена контрольная работа по теме «Преобразование тригонометрических выражений». Цель работы – установить уровень сформированности познавательного интереса. Со всеми самостоятельными и контрольными работами учащихся можно ознакомиться в Приложении «Работы учащихся».
Фрагмент урока №10 по теме «Преобразование тригонометрических выражений» (18.12.2009г).
Тип урока: контроля.
Цели:
образовательные
: выявить уровень знаний, умений и навыков по применению формул преобразования тригонометрических выражений;
воспитательные
: воспитывать внимание, умение работать самостоятельно, самостоятельно принимать правильное решение;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, находить оптимальные пути решения, решать проблему, формирование познавательного интереса к математике.
Этап урока: контрольная работа.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(
создает ситуацию
)
- У каждого на столах лежат бланки для решений и ответов на контрольную работу и черновики. Подпишите на них свою фамилию и номер варианта.
- Контрольная работа состоит из трех частей: Части А, где даны простейшие задания с вариантами ответов. Часть В содержит более сложные задания, требующие решения. Здесь вы записываете только ответ. В Части С вы описываете решение каждого задания подробно. Критерии оценивания: правильно решенная только Часть А на «3», Часть А и Часть В на «4», Часть А, Часть В и Часть С на «5». Время пошло
|
(рассматривают пример, анализируют ситуацию, выдвигают гипотезы по определению возможных проблем и выделяют основную проблему, находят пути решения и решают ситуацию)
|
Задание № 13.
1 вариант
1.Дан корень уравнения  . .
2.Дано равенство 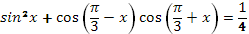 . Сформулируйте и запишите задание и решите его. . Сформулируйте и запишите задание и решите его.
2 вариант
1
.Дан корень уравнения  . .
2.
Дано равенство . Сформулируйте и запишите задание и решите его.
|
Контроль № 3.
Контрольная работа на тему «Преобразование тригонометрических выражений».
Вариант 1.
Часть А.
1. Упростите выражение
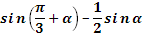 . .
а)  ; б) ; б) 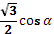 ; в) ; в)  ; г) ; г)  . .
2. Вычислите
 . .
а)  ; б) ; б) 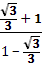 ; в) ; в)  ; г) ; г)  . .
3. Упростите выражение
 . .
а) 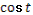 ; б) ; б) 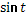 ; в) ; в) 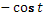 ; г) ; г) 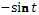 . .
4. Упростите выражение
 . .
а) 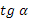 ; б) ; б) 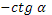 ; в) ; в) 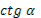 ; г) ; г)  . .
5. Вычислите
 . .
а) 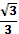 ; б) ; б) 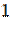 ; в) ; в) 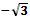 ; г) ; г)  . .
6. Вычислите
 . .
а) 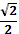 ; б) ; б) 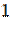 ; в) ; в)  ; г) ; г) 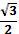 . .
Часть В.
1.
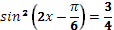 . Сформулируйте задание и решите его. . Сформулируйте задание и решите его.
2.
Представьте в виде произведения 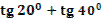 . .
Часть С.
1.
Дан корень уравнения  . .
2.
Дано равенство 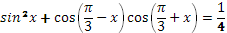 . Сформулируйте и запишите задание и решите его. . Сформулируйте и запишите задание и решите его.
Контрольная работа на тему «Преобразование тригонометрических выражений».
Вариант 2.
Часть А.
1. Упростите выражение
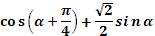 . .
а)  ; б) ; б) 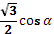 ; в) ; в)  ; г) ; г)  . .
2. Вычислите
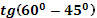 . .
а)  ; б) ; б) 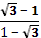 ; в) ; в) 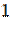 ; г) ; г)  . .
3. Упростите выражение
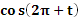 . .
а) 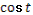 ; б) ; б) 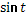 ; в) ; в) 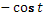 ; г) ; г) 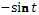 . .
4. Упростите выражение
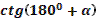 . .
а) 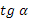 ; б) ; б) 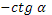 ; в) ; в) 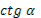 ; г) ; г)  . .
5. Вычислите
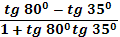 . .
а) 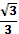 ; б) ; б) 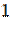 ; в) ; в) 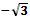 ; г) ; г)  . .
6. Вычислите
 . .
а) 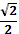 ; б) ; б) 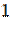 ; в) ; в)  ; г) ; г) 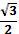 . .
Часть В.
1.
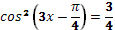 .
Сформулируйте задание и решите его. .
Сформулируйте задание и решите его.
2.
Представьте в виде произведения 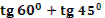 . .
Часть С.
1
.
Дан корень уравнения  . .
2.
Дано равенство . Сформулируйте и запишите задание и решите его.
Контрольная работа состояла из трех частей А, В и С.
Критерии оценивания 1 кейс-задания:
1. Верно определена проблема.
2. Правильно выполнены преобразования.
3. Применение формул преобразования тригонометрических выражений.
4. Найдено уравнение.
«5» - 4 пункта.
«4» - 3 пункта.
«3» - 2 пункта.
«2» - 1 пункт и менее.
Критерии оценивания 2 кейс-задания:
1. Верно определена проблема.
2. Правильно выполнены преобразования.
3. Применение формул преобразования тригонометрических выражений.
4. Найден ответ.
«5» - 4 пункта.
«4» - 3 пункта.
«3» - 2 пункта.
«2» - 1 пункт и менее.
Критерии оценивания контрольной работы:
«5» - верно выполнены части А, В и С (IV уровень).
«4» - верно выполнены части А и В (III уровень).
«3» - верно выполнена часть А (II уровень).
«2» - менее части А (I уровень).
Объединяя все задания, часть А формирует I уровень познавательного интереса, часть В – I, II и III уровни познавательного интереса, часть С – I, II, III и IV уровни познавательного интереса.
Выполнена статистическая обработка материала. Проведен анализ по следующим признакам: отметка, уровень сформированности познавательного интереса и составлен вариативный ряд (Приложение 13).
| Оценка |
"2" |
"3" |
"4" |
"5" |
| Количество учащихся |
1 |
10 |
12 |
4 |

| Уровень |
I уровень |
II уровень |
III уровень |
IV уровень |
| Количество учащихся |
1 |
10 |
12 |
4 |
| 4% |
37% |
44% |
15% |
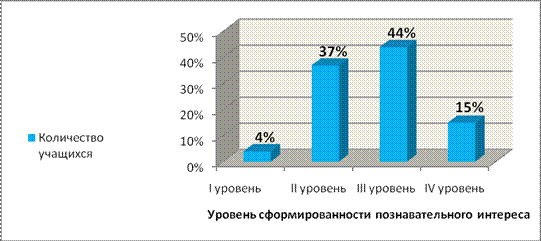
Таким образом, 4% учащихся остались на I уровне сформированности познавательного интереса, 37% - имеют Iи IIуровни, 44% - I, IIи III уровни и 15% - I, II, III и IV уровни.
Повышение качества обучения можно проследить по графику:

Анализ результатов диагностического исследования показал, что на начало эксперимента познавательный интерес Iуровня был сформирован у 27% учащихся, Iи II уровней – у 38%, I, II и III уровней – у 23%, I, II, III и IV уровней – у 11%. На конец эксперимента познавательный интерес I уровня сформирован у 4% учащихся, Iи II уровней – у 37%, I, II и III уровней – у 44%, I, II, III и IV уровней – у 15%. Наглядно эти результаты представлены в виде следующего графика:
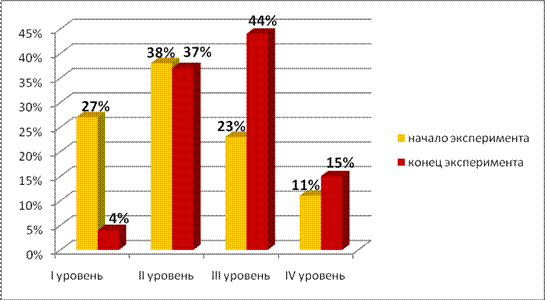
- Итоговое анкетирование.
Цель – выяснить, изменилось ли отношение учащихся к предмету, повысился ли интерес.
Анкета состояла из 19 вопросов (открытые, с вариантами ответов). С анкетами учащихся можно ознакомиться в Приложении 14, с анализом анкет – Приложение 15. В ходе проведения анкетирования были получены следующие результаты:
- 82% учащихся относятся к математике положительно, 17% - нейтрально;
- 56 % учащихся хотели бы изучать математику углубленно, 31 % ответили отрицательно, 13 % не дают однозначного ответа;
- 87% учащихся считают математику интересным предметом, 53% из которых изучают данный предмет с целью удовлетворения своего интереса.
- На вопросы о проблемном обучении 90% учащихся ответили положительно.
Проанализировав полученные результаты и сравнив с результатами анкетирования на начальном диагностирующем этапе, можно сделать вывод: у учащихся наблюдается тенденция к повышению интереса к математике, многие стали изучать предмет не только с целью поступления в ВУЗ или сдаче ЕГЭ, но и с целью удовлетворения интереса к предмету и получения знаний.
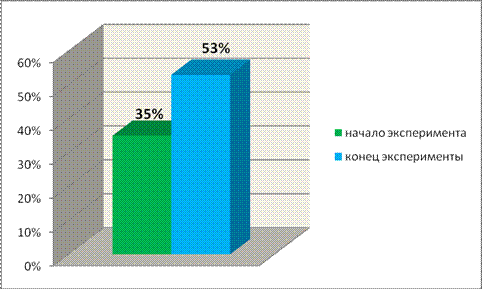
Вывод:
Внедрение метода кейсов в обучение способствовало повышению уровня познавательного интереса учащихся на 18%. Что говорит об эффективности разработанной методики.
В процессе работы над темой диплома были решены следующие задачи:
- изучена и проанализирована психолого-педагогическая и методическая литература по теме исследования;
- проанализирована сущность кейс-метода обучения, изучены перспективы его развития и внедрения в образовательный процесс, определены основные трудности и проблемы;
- выделены уровни сформированности познавательного интереса с помощью умений решать кейсы;
- разработана методика изучения темы «Преобразование тригонометрических выражений», направленная на формирование познавательного интереса;
- проведено экспериментальное обучение и проанализированы полученные результаты.
Педагогический эксперимент показал достоверность выдвинутой гипотезы исследования, что позволило сделать вывод об эффективности разработанной методики. Таким образом, гипотеза исследования экспериментально подтверждена, цель исследования достигнута.
Экспериментальное исследование проходило в МОСШ № 32 г. Нижневартовска, в 10А
классе, учитель математики Одобеско Нина Михайловна.
В рамках дипломной работы выступала на XII студенческой научной конференции НГГУ в апреле 2010 г., были написаны тезисы «Метод кейсов как средство формирования познавательного интереса учащихся при изучении темы «Преобразование тригонометрических выражений» в 10 классе».
Активизация познавательной деятельности
– это побуждение к энергичному, целенаправленному учению.
Метод
(от греческого слова «metodos» — буквально путь к чему-либо) – это способ достижения цели, определенным образом упорядоченную деятельность.
Метод кейсов
или метод конкретных ситуаций – это метод активного проблемно-ситуационного анализа, основанный на обучении путем решения конкретных задач – ситуаций (решение кейсов).
Метод обучения
– это способ упорядоченной взаимосвязанной деятельности преподавателя и обучаемых, деятельности, направленной на решение задач образования, воспитания и развития в процессе обучения.
Педагогическая ситуация
– это факт, жизненная история, с которой учитель столкнулся в повседневной работе и которая породила педагогические задачи, требующие решения.
Познавательный интерес
– это стремление человека обращать на что-то внимание, познавать какие-либо предметы и явления.
Познавательный интерес
– это глубинный внутренний мотив, основанный на свойственной для человека врожденной познавательной потребности.
Ситуация
(от средневекового лат. situatio – положение) – это сочетание условий и обстоятельств, создающих определенную обстановку, положение.
Средство обучения
– это материальный или идеальный объект, который «помещен» между учителем и учащимися и использован для усвоения знаний, формирования опыта познавательной и практической деятельности.
1. Алгебра и начала математического анализа. 10 класс: задачник для учащихся образовательных учреждений./[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. М.: Мнемозина, 2008. – 273 с.
2. Алгебра и начала математического анализа. 10 класс: задачник для учащихся образовательных учреждений (профильный уровень)./[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 2-е изд. доп. М.: Мнемозина, 2008. – 264 с.
3. Алгебра и начала математического анализа. 10 класс: учебник для учащихся образовательных учреждений./[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. М.: Мнемозина, 2008. – 293 с.
4. Алгебра и начала математического анализа. 10 класс: учебник для учащихся образовательных учреждений (профильный уровень)./[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 2-е изд. доп. М.: Мнемозина, 2008. – 287 с.
5. Багиев Г.Л., Наумов. В.Н. Кейсовый метод в системе обучения на практических занятиях [Электронный ресурс]. – Режим доступа:www.marketing.spb.ru. – 15.04.2009 г.
6. Виноградова Л.В. Методика преподавания математики в средней школе: учебное пособие. – Ростов н/Д.: Феникс, 2005. – 252с.: ил. – (Здравствуй, школа!).
7. Выгодский М.Я. Арифметика и алгебра в древнем мире. Москва.,1967г.
8. Гозман О., Жаворонкова А., Рубальская А. Метод кейсов [Электронный ресурс]. – Режим доступа:www.ru.wikipedia.org. – 20.04.2009г.
9. Гоноболин Ф.Н. Внимание и его воспитание. – Москва., 1972г.
10. Долгоруков А. Метод case-study как современная технология профессионально ориентированного подхода [Электронный ресурс]. – Режим доступа:www.evolkov.net. – 30.04.2009 г.
11. Духновский С.В. Психологическое сопровождение подростков в критических ситуациях[Электронный ресурс]. – Режим доступа: http://window.edu.ru/window_catalog/pdf2txt?p_id=33563. – 08.03.2010 г. (4)
12. Журавлев В.И. Педагогика: учебное пособие для студентов педагогических вузов и педагогических колледжей.– Москва: под ред. П.И. Пидкасистого, 1996г.
13. Зайцева И.А. Формирование познавательного интереса к учению как способ развития креативных способностей личности [Электронный ресурс]. – Режим доступа:www.zaitseva-irina.ru. – 26.04.2009 г.
14. Карасева В.В. Развитие познавательного интереса при обучении математике [Электронный ресурс]. – Режим доступа:www.edusite.ru. – 3.05.2009 г.
15. Карташова Л.И. Способы формирования познавательных интересов старшеклассников.//Математика. – 2001. – №20. – С.10-16.
16. Ким К.К., Микляева И.В. К вопросу о повышении эффективности работы учащихся на уроках.//Математика в школе. – 1994. – №3. – С.16-17.
17. Компетентностный подход в педагогическом образовании: коллективная монография /под редакцией проф. В.А. Козырева, проф. Н.Ф. Радионовой и проф. А.П. Тряпицыной. – Санкт-Петербург: РГПУ им. А.И. Герцена, 2008г.
18. Кузьмина В.Г. Активизация познавательной деятельности учащихся.//Математика в школе. – 1996. – №4. – С.15-16.
19. Кульневич С.В., Лакоценина Т.П. Современный урок. Часть III: Проблемные уроки. Научно-практич: пособие для учителей, методистов, руководителей учебных заведений, студентов и аспирантов пед. учеб. заведений, слушателей ИПК. – Ростов н/Д: Изд-во «Учитель», 2006. – 288 с.
20. Махмутов М.И. Организация проблемного изучения в школе. – М., 1977. С. 94-96.
21. Медникова Н.А., Скулов П.В. Проблемное обучение на уроках физики [Электронный ресурс]. – Режим доступа: http://student.km.ru/ref_show_frame.asp?id=E1342ECEFE224B81BF73443FE8D39A6A . – 10.01.2010 г.(5)
22. Педагогика. //Под редакцией Ю. К. Бабанского., - «Просвещение», Москва, 1983 г.
23. Педагогика: Учебное пособие для студентов педагогических вузов и педагогических колледжей/под редакцией П.И. Пидкасистого. – М.: Российское педагогическое агентство, 1996. – 602 с. (1)
24. Приказ о концепции модернизации российского образования на период до 2010 года [Электронный ресурс]: Российское образование. Федеральный портал: нормативные документы/ Информационное сопровождение: Простяков С.А. – Режим доступа: http://www.edu.ru/db/mo/Data/d_02/393.html
. - 15.04.2010.
25. Программы для общеобразовательных школ, гимназий, лицеев: Математика 5-11 классы /Составитель Г.М. Кузнецова, Н.Г. Миндюк. – 4-е издание. – М.: Дрофа, 2004. – 320 с. (7)
26. Рожкова, Ковалев. Окно в ситуационную методику обучения [Электронный ресурс]. – Режим доступа:www.casemethod.ru. – 15.04.2009 г.
27. Рыжова Г.И. Развитие познавательного интереса и творческой активности у учащихся на уроках информатики [Электронный ресурс]. – Режим доступа:www.festival1.1september.ru. – 8.05.2009г.
28. Таймасханов У.Д. Создание проблемных ситуаций.//Математика в школе. – 1994. – №5. – С.16-18.
29. Тамбовкина Т.И. Педагогическая ситуация [Электронный ресурс]. – Режим доступа: http://nsc.1september.ru/2006/16/6.htm. – 18.02.2010 г. (3)
30. Харламов. Как активизировать учение школьников: дидактические очерки. – Минск., 1975г.
31. Что такое Ситуация? Значение и толкование слова situatsija, определение термина [Электронный ресурс]. – Режим доступа: http://www.onlinedics.ru/slovar/bes/s/situatsija.html. – 26.01.2010 г.(2)
32. Шачков В.В. Развитиетворческих способностейиформированиепознавательногоинтереса учащихся [Электронный ресурс]. – Режим доступа: http://chesly.narod.ru/Doklad_razvitie.html.–21.01.2010 г.(6)
33. Шеронова А.В. Занимательные фрагменты уроков.//Математика в школе. – 2002. – №1. – С.37-38.
34. Щукина Г.И. Актуальные вопросы формирования интереса в обучении. Москва: «Просвещение», 1984г.
Фрагмент урока №2 по теме «Формулы двойного аргумента» (25.11.2009г).
Тип урока: закрепление.
Цели:
образовательные
: закрепить умения применения формул двойного аргумента;
воспитательные
: воспитать внимание, умение работать самостоятельно;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, находить оптимальные пути решения, решать проблему, формирование познавательного интереса к математике.
Этап урока: самостоятельная работа.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(
создает ситуацию
)
- На листочках подпишите фамилию, имя, «Самостоятельная работа» и номер варианта. Я раздала вам карточки. Каждая карточка содержит по 5 заданий. В первом задании необходимо упростить выражение, во втором – вычислить значение выражения, в третьем – решить уравнение, в четвертом – доказать тождество. В пятом задании даны корни уравнения, вам необходимо найти выход из ситуации. Это задание со звездочкой на отдельную оценку. Время для работы 20 минут. Критерии оценивания: 4 задания на «5», 3 задания - «4», 2 задания на «3» и соответственно меньше двух заданий «2». Время пошло. Приступаем к выполнению заданий.
|
(рассматривают пример, анализируют ситуацию, выдвигают гипотезы по определению возможных проблем и выделяют основную проблему, находят пути решения и решают ситуацию)
|
Задание № 3.
1 вариант.
Даны корни уравнения 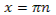 и . Составьте уравнение и решите его. и . Составьте уравнение и решите его.
2 вариант.
Даны корни уравнения 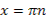 и и  . Составьте уравнение и решите его. . Составьте уравнение и решите его.
|
Самостоятельная работа.
Вариант 1.
4.
Вычислите:
.
5.
Упростите выражение:
 . .
6.
Решите уравнение:
 . .
7.
Докажите тождество:
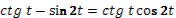 . .
5*
.
Даны корни уравнения 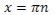 и . Составьте уравнение и решите его. и . Составьте уравнение и решите его.
|
Самостоятельная работа.
Вариант 2.
1.
Вычислите:
.
2.
Упростите выражение:
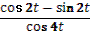 . .
3.
Решите уравнение:
 . .
4.
Докажите тождество:
 . .
5*
.
Даны корни уравнения  и и  . Составьте уравнение и решите его. . Составьте уравнение и решите его.
|
В самостоятельной работе первые четыре задания общего характера, 5 задание, содержащее кейс – на формирование I, II, III и IV уровней познавательного интереса.
Общие критерии оценивания первых четырех заданий:
«5» - 4 задания.
«4» - 3 задания.
«3» - 2 задания.
«2» - менее 2 заданий.
Критерии оценивания кейс-задания:
5. Верно определена проблема.
6. Правильно выполнены преобразования.
7. Применение формул преобразования тригонометрических выражений.
8. Найдено уравнение.
«5» - 4 пункта (IV уровень).
«4» - 3 пункта (III уровень).
«3» - 2 пункта (II уровень).
«2» - 1 пункт и менее (I уровень).
Фрагмент урока №3 по теме «Формулы понижения степени» (30.11.2009г).
Тип урока: изучение нового материала.
Цели:
образовательные
: изучить формулы понижения степени и отработать умения по их применению;
воспитательные
: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: изучение нового материала.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
- Перейдем к изучению нового материала. Откройте тетради, запишите число и тему урока «Формулы понижения степени».
(
предлагает практический пример и создает ситуацию
)
- Скажите, пожалуйста, чему равен  по формуле двойного аргумента? по формуле двойного аргумента?
(предлагает систему вопросов для анализа ситуации)
- Как мы можем здесь поступить, чтобы остались только косинусы?
Учитель вызывает к доске ученика для вывода формулы.
- Выполним действия.
(подводит учащихся к формулированию проблем)
- Обратите внимание на тему урока.
- Что нам нужно выразить?
(решение проблемы)
- Выражаем.
- Молодец. Садись.
(анализ полученных результатов)
- Таким образом, что мы получили?
- Возьмите ее в рамочку.
(анализ данных и выдвижение гипотез)
- Как из первого тождества можно получить формулу понижения степени для синуса?
Учитель вызывает к доске ученика для вывода формулы.
(решение проблемы)
- Выполняем действия.
(анализ полученных результатов)
- Таким образом, какую формулу мы вывели?
- Молодец. Садись. Возьмите в рамочку формулу.
- Как вы думаете, откуда появилось такое название формул?
- Что произошло со степенью?
- Обратите внимание, степень понижается. А что происходит с аргументом?
- Полученные две формулы называют также формулами половинного аргумента, поскольку они позволяют, зная значение  , найти значения синуса и косинуса половинного аргумента. , найти значения синуса и косинуса половинного аргумента.
- Также с помощью этих формул можно найти тангенс половинного аргумента.
Учитель вызывает к доске ученика для вывода формулы.
- Записываем 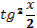 равно чему? равно чему?
- Молодец. Садись.
- Запишите формулу и возьмите в рамочку.
|
-  . .
(анализируют ситуацию)
- Заменить 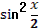 по основному тригонометрическому тождеству на по основному тригонометрическому тождеству на 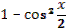 . .
Один ученик выходит к доске. Остальные выполняют в тетрадях.
(выдвигают гипотезы по определению возможных проблем)
-  . .
- 
- 
- Формулу понижения степени для косинуса.
(анализируют данные и выдвигают гипотезы)
- Заменить  по основному тригонометрическому тождеству на по основному тригонометрическому тождеству на 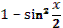 . .
Один ученик выходит к доске. Остальные выполняют в тетрадях.
 . .
- Отсюда  . .
- Формулу понижения степени для синуса.
- В левой части тождеств содержится вторая степень косинуса или синуса, а в правой части – первая степень косинуса.
- Она понизилась.
- Он удваивается.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
- 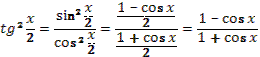 . .
- Мы вывели три формулы понижения степени.
|
Задание № 4.

 . .
 . .
 . .
 . .
 . .
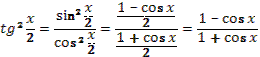 . .
 . .
|
Фрагмент урока №4 по теме «Формулы понижения степени» (30.11.2009г).
Тип урока: закрепление.
Цели:
образовательные
: отработать умения по применению формул двойного аргумента;
воспитательные
: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: закрепление.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(создает ситуацию)
- Дан корень уравнения  . .
(подводит учащихся к формулированию проблем)
- Что мы можем с ними сделать?
- Каким должно быть уравнение?
- А еще каким?
(анализ данных)
- Как мы помним из прошлого урока надо рассуждать снизу вверх.
- Раз перед  стоит стоит  , какая получается функция? , какая получается функция?
- Что мы сделаем, чтобы получить ответ простейшего уравнения.
(выдвижение гипотез)
- Этот ответ какого простейшего уравнения?
(поиск путей решения и решение проблемы)
- Какую формулу мы должны применить?
- Как должно выглядеть уравнение по формуле?
- Но из этого как-то должно получаться  . .
- На что можно домножить, что нужно добавить или отнять?
- Правильно. Отсюда получится  ? ?
- Давайте перенесем  вправо, которая получается делением вправо, которая получается делением  на 2, и запишем, что получится. на 2, и запишем, что получится.
- Что можем сделать в левой части?
- И чему это равно?
- Чтобы в левой части остался только косинус, что сделаем?
- И что получится?
|
(выдвигают гипотезы по определению возможных проблем и выделяют основную проблему)
- Найти уравнение, которому принадлежат эти корни.
- Тригонометрическим.
- На тему урока.
(анализируют данные)
- Косинус.
- Домножим обе части на 6 и получим
.
(выдвигают гипотезу)
-  . .
- Формулу понижения степени.
- 
- Надо числитель умножить на 2 и отнять в числителе 2. Получится 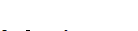 . .
- Да.
-
- Вынести в числителе 2 за скобки. Получим 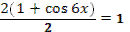 . .
-
- Перенесем 2 в правую часть.
- 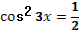 . .
- Мы получили уравнение.
|
Задание № 5.

 . .
.
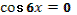 . .
 . .
.
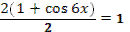 . .
.
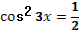 . .
|
Фрагмент урока №5 по теме «Преобразование суммы тригонометрических функций в произведение» (02.12.2009г).
Тип урока: изучение нового материала.
Цели:
образовательные
: изучить формулы преобразования суммы тригонометрических функций в произведение и отработать умения по применению формул двойного аргумента;
воспитательные
: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: изучение нового материала.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(
предлагает практический пример и создает ситуацию
)
- Рассмотрим выражение 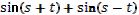 . .
(предлагает систему вопросов для анализа ситуации)
- По каким формулам мы можем разложить  и и  ? ?
Учитель вызывает одного ученика к доске.
(поиск путей решения и решение проблемы)
- Выполним разложение.
- Итак, получается  . .
- Введем новые переменные. Заменим 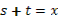 , , 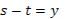 . .
- Сложим эти равенства. Что получим?
- Отсюда, чему равно  ? ?
- А если от  отнять отнять  , то что получим? , то что получим?
- Выразим 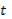 . .
- Подставим теперь в формулу  полученные значения. полученные значения.
- Что получим?
- Молодец. Садись.
(анализ полученных результатов)
- Какую формулу мы вывели?
- Возьмите формулу в рамочку.
- Выведем формулу преобразования разности синусов в произведение.
(анализ данных)
- Скажите, пожалуйста, чему равен 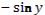 ? ?
(решение проблемы)
- Подставим в полученную формулу 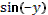 . .
Учитель вызывает одного ученика к доске.
- Что получим?
- Молодец. Садись.
- Выпишем формулу. Возьмите ее в рамочку.
(создает ситуацию
)
- А теперь рассмотрим выражение 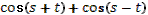 . .
(подводит учащихся к формулированию проблем)
- Что нужно сделать?
- Проделаем те же преобразования с косинусами, что и с синусами самостоятельно в тетрадях. Выводим формулу преобразования суммы косинусов в произведение и разности косинусов в произведение.
- Заметьте, так как косинус функция четная, то разность в этом случае, выводится, как и сумма. То есть для вывода преобразования разности косинусов в произведение рассматриваем выражение 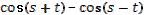 . .
- Я попрошу двух учеников выйти к доске и записать выводы формул преобразования суммы косинусов в произведение и разности косинусов в произведение.
Учитель вызывает двух учеников к доске.
- Молодцы. Садитесь. Таким образом, мы вывели 4 формулы.
- Данные формулы особенно полезны при решении тригонометрических уравнений, поскольку они позволяют сумму или разность синусов или косинусов разложить на множители.
|
(рассматривают пример)
(анализируют ситуацию)
- По формулам синуса суммы и разности аргументов.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
- 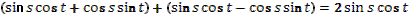 . .
-  . .
- 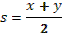 . .
-  . .
-  . .
- 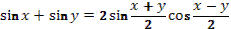 . .
- Формулу преобразования суммы синусов в произведение.
(анализируют данные)
- 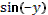 . .
Один ученик выходит к доске. Остальные выполняют в тетрадях.
- 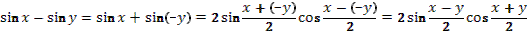 . .
-  . .
(выдвигают гипотезы по определению возможных проблем и формулируют проблему)
- выразить формулу преобразования суммы косинусов в произведение и разности косинусов в произведение.
Дети самостоятельно в тетрадях выводят формулы.
(находят пути решения и решают ситуацию)
Два ученика выходят к доске и выводят формулы. Остальные следят за доской и сверяются.
-
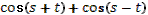 . .
- 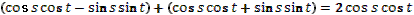 . .
- 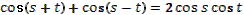 . .
-  , , 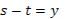
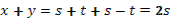 . .
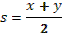 . .
 . .
 . .
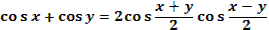 . .
- 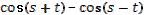 . .
-  . .
-  . .
 . .
|
Задание № 8.
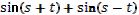
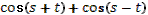
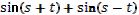 . .
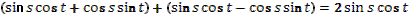 . .
 . .
 , , 
 . .
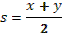 . .
 . .
 . .
 . .
 . .
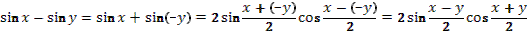 . .
 . .
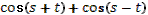 . .
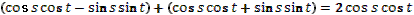 . .
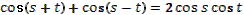 . .
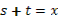 , , 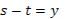
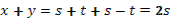 . .
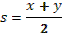 . .
 . .
 . .
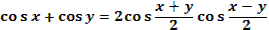 . .
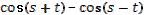 . .
 . .
 . .
 . .
|
Фрагмент урока №6 по теме «Преобразование суммы тригонометрических функций в произведение» (02.12.2009г).
Тип урока: закрепление.
Цели:
образовательные
: отработать умения по применению формул преобразования суммы тригонометрических функций в произведение;
воспитательные
: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: закрепление.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(создает ситуацию)
- Дано выражение  . .
(подводит учащихся к формулированию проблем)
- Что мы можем с ним сделать? Сформулируйте задание.
- Какие еще варианты?
(анализ данных и выдвижение гипотез)
- А как? Ведь мы знаем формулы преобразования разности только синусов или косинусов.
Учитель вызывает одного ученика к доске.
- Молодец. Садись.
(подводит учащихся к формулированию проблем)
- А теперь сформулируйте вопрос для такого выражения,
 . .
- А еще?
(анализ данных)
- Мы раньше с вами преобразовывали выражение с помощью формул приведения в виде, например
 . А можем ли мы проделать обратную операцию, то есть . А можем ли мы проделать обратную операцию, то есть  преобразовать в преобразовать в  ? ?
- А что тогда будет за функция в нашем случае?
(выдвижение гипотез)
- Какое теперь мы можем сформулировать задание для нашего выражения?
Учитель вызывает одного ученика к доске.
(поиск путей решения и решение проблемы)
- Молодец. Садись.
|
(выдвигают гипотезы по определению возможных проблем и выделяют основную проблему)
- Решить уравнение.
- Представить разность в виде произведения.
(анализируют данные и выдвигают гипотезы)
- Представим  как как 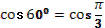 . .
И подставим в выражение.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
- Разложим по формуле преобразования разности косинусов в произведение. Получим 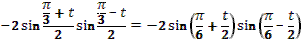 . .
(выдвигают гипотезы по определению возможных проблем)
- Решить уравнение.
- Упростить выражение.
(анализируют данные)
- Да.
-  . .
(выдвигают гипотезу)
- Представить сумму косинусов в виде произведения.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
- Разложим по формуле преобразования суммы косинусов в произведение. Получим .
- Раскроем скобки в числителе и получим  . .
|
Задание № 9.
 . .

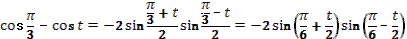 . .
 . .
 . .
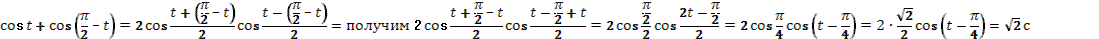 . .
|
Фрагмент урока №7 по теме «Преобразование произведения тригонометрических функций в сумму» (14.12.2009г).
Тип урока: изучение нового материала.
Цели:
образовательные
: изучить формулы преобразования произведения тригонометрических функций в сумму и отработать умения по их применению;
воспитательные
: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: изучение нового материала.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
- Перейдем к изучению нового материала.
- Откройте тетради и запишите число, «Классная работа» и тему урока «Преобразование произведений тригонометрических функций в суммы».
(
предлагает практический пример и создает ситуацию
)
-
- Сравните названия этой темы с предыдущей. Что вы можете сказать?
- На прошлом уроке мы вывели формулы…?
- Известно, что любая математическая формула на практике применяется как справа налево, так и слева направо.
(предлагает систему вопросов для анализа ситуации)
- На прошлом уроке мы нашли, что  , , 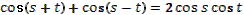 , ,  . .
- Что вы видите в этих формулах?
(подводит учащихся к формулированию проблем)
- А какую задачу мы поставили перед собой?
- И что мы можем сделать с этими формулами?
Учитель вызывает трех учеников к доске для вывода формул.
- Молодцы. Садитесь.
- Таковы три формулы, позволяющие преобразовать произведение тригонометрических функций в сумму.
- Обведите их в рамочку.
|
(рассматривают пример)
- Раньше мы преобразовывали суммы и разности тригонометрических функций в произведение. А сегодня наоборот произведение тригонометрических функций в суммы.
- Преобразовывали суммы и разности тригонометрических функций в произведение.
(анализируют ситуацию)
- Слева сумма тригонометрических функций, а слева произведение.
(выдвигают гипотезы по определению возможных проблем)
- Вывести формулы преобразования произведений тригонометрических функций в суммы.
- Выразить из них произведение косинусов, синусов и произведение косинуса на синус.
Три ученика у доски выводят формулы. Остальные выполняют в тетрадях.
(находят пути решения и решают ситуацию)
1) . .
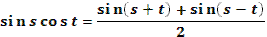 . .
2)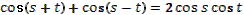 . .
 . .
3) . .
 . .
|
Задание № 10.
1) . .
2)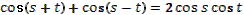 . .
3) . .
1) . .
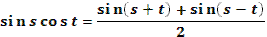
2)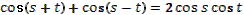 . .

3) . .

|
Фрагмент урока №9 по теме «Преобразование тригонометрических выражений» (18.12.2009г).
Тип урока: закрепление.
Цели:
образовательные
: отработать умения по применению формул преобразования тригонометрических выражений;
воспитательные
: воспитать внимание, умение отвечать на вопросы, аргументировать свою точку зрения,;
развивающие
: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, находить оптимальные пути решения, решать проблему, формирование познавательного интереса к математике.
Этап урока: закрепление.
| Деятельность учителя
|
Деятельность учащихся
|
Вид доски
|
(
создает ситуацию
)
- На доске вывешены все формулы, которые мы изучили.
- Перейдем к решению заданий. Откройте тетради, запишите число, «Классная работа».
- У каждого на столах лежат карточки с заданиями, которые необходимо решить всем за этот урок самостоятельно. Все решения выполняем в тетрадях, в конце урока тетради сдаем на проверку. Критерии оценивания: Верно решенные 4-5 заданий «5», 3 задания «4», 2 задания «3», менее двух заданий «2».
- Также некоторым из вас я раздала индивидуальные карточки с заданиями. Их решение выполняем у доски, также самостоятельно.
- Для решения индивидуальных карточек к доске выходим по два человека. Сначала выходят карточка № 1 и карточка №2, и так далее.
- Если возникают какие-либо вопросы по решению, поднимайте руки, я подойду.
- Приступаем к работе.
Учитель контролирует и консультирует.
|
(рассматривают 5 пример, анализируют ситуацию, выдвигают гипотезы по определению возможных проблем и выделяют основную проблему, находят пути решения и решают ситуацию)
|
Задание № 12.
Дано, что  , , 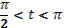 и и  . Сформулируйте и запишите задание и решите его. . Сформулируйте и запишите задание и решите его.
|
Карточка № 1.
Докажите тождество
 . .
|
Карточка № 2.
Решите уравнение
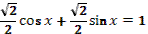
|
Карточка № 3.
Известно, что 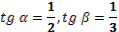 . .
Вычислите 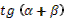 . .
|
Карточка № 4.
Упростите выражение

|
Карточка № 5.
Известно, что  , ,  . Вычислите: . Вычислите: 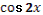 . .
|
Карточка № 6.
Вычислите 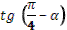 , ,
если 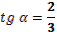 . .
|
Карточка № 7.
Докажите тождество

|
Карточка № 8.
Решите уравнение
|
Карточка № 9.
Представьте в виде произведения
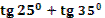
|
Карточка № 10.
Решите уравнение
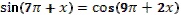
|
Карточка № 11.
Сравните числа
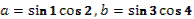
|
Карточка № 12.
Решите уравнение
|
Карточка с заданиями.
Преобразование тригонометрических выражений.
1.
Упростите выражение:
 ; ;
2.
Вычислите:
а) 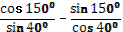 ; ;
б)  . .
3.
Докажите тождества:
а) 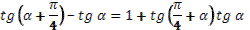 ; ;
б)  . .
4.
Решите уравнения:
а) 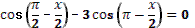 ; ;
б) 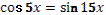 . .
5.
Дано, что  , , 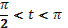 и и  . Сформулируйте и запишите задание и решите его. . Сформулируйте и запишите задание и решите его.
В работе первые четыре задания общего характера, 5 задание – на формирование I, II, III и IV уровней познавательного интереса.
Общие критерии оценивания первых четырех заданий:
«5» - 4 задания.
«4» - 3 задания.
«3» - 2 задания.
«2» - менее 2 заданий.
Критерии оценивания кейс-задания:
1. Правильно сформулировано задание.
2. Правильно выполнены преобразования.
3. Применение формул преобразования тригонометрических выражений.
4. Найден ответ.
«2» - менее 2 пунктов (I уровень).
«3» - 2 пункта (II уровень).
«4» - 3 пункта (III уровень).
«5» - 4 пункта (IV уровень).
Программа эксперимента
| №этапа
|
Этапы эксперимента
|
Цель
|
Виды групп
|
Требования к комплектации групп
|
Измеряемые величины
|
Перечень экспериментальных действий
|
Методы
|
Средства и материал
|
| 1 |
Констатирующий |
Разработать методику формирования познавательного интереса на уроках математики с помощью кейс технологии, систему заданий, анкеты. |
Константная методика организации эксперимента. |
Формируется одна группа. Результаты эксперимента сопоставляются с исходными данными. |
Уровень умений решать проблемные ситуации:
1) любопытство,
2) любознательность
3) собственно познавательный интерес,
4) творческий интерес
|
Составление системы вопросов для интервью и анкет, методического материала. |
Эмпирические и теоретические методы. Наблюдение за работой учителя, беседа, наблюдение за деятельностью учащихся. |
Листы опроса, протоколы наблюдений, методические указания и рекомендации и т.д. |
| 2 |
Диагностический |
Провести диагностику умений находить, создавать и решать проблемные ситуации, направленные на формирование познавательного интереса. |
Уровень умений решать проблемные ситуации, направленные на формирование познавательного интереса:
1) любопытство,
2) любознательность
3) собственно познавательный интерес,
4) творческий интерес.
|
Проводится анкетирование, интервью, анализ данных, вводная контрольная работа. Делается вывод. |
Методы сбора и накопления данных. Анкетирование, контрольный срез, количественный и качественный анализ данных, |
Листы опроса, контрольные задания, система задач, интерактивная доска, проектор, компьютер и т.д. |
| 3 |
Формирующий |
Формирование умений находить, создавать и решать проблемные ситуации с помощью кейс технологии, направленные на формирование познавательного интереса. |
Уровень умений решать проблемные ситуации с помощью кейс технологии, направленные на формирование и повышение познавательного интереса:
1) любопытство,
2) любознательность
3) собственно познавательный интерес,
4) творческий интерес.
|
Внедрение методики, создание методических условий для проверки эффективности кейс технологии. |
Методы конструирования явлений. Создание определенных педагогических и психологических ситуаций, экспериментальное обучение. |
Конспекты уроков, методические указания и рекомендации, контрольные задания, система задач, интерактивная доска, проектор, компьютер и т.д. |
| 4 |
Диагностический |
Провести исследование и выяснить, насколько сформировались умения находить, создавать и решать проблемные ситуации с помощью кейс технологии, направленные на формирование познавательного интереса. |
Уровень сформированности умений решать проблемные ситуации, направленные на повышение познавательного интереса:
1) любопытство,
2) любознательность
3) собственно познавательный интерес,
4) творческий интерес.
|
Проводится анкетирование, интервью, анализ, контрольный работа, обработка статистических данных. Делается вывод. |
Методы контроля и измерений. |
Листы опроса, контрольные задания, система задач, интерактивная доска, проектор, компьютер и т.д. |
Анкета для учащихся.
1.
Как Вы относитесь к математике?
1) Положительно;
2) Отрицательно;
3) Нейтрально.
2.
Как Вам дается изучение математики?
1) Легко;
2) Сложно;
3) Вообще не дается.
3.
Интересна ли Вам математика?
1) Интересна;
2) Не интересна;
3) Другой ответ____________________________________________________
4.
С какой целью Вы изучаете математику?__________________________________________________
__________________________________________________________________
5.
Какими проблемными методами на уроках математики Вам излагается материал?
1) Проблемное изложение;
2) Исследованием;
3) Творческим обучением;
4) Поисковым или частично-поисковым методом;
5) Репродуктивным;
6) Другой ответ____________________________________________________
6.
На какую оценку Вы оцениваете свои знания по математике?
1) 5;
2) 4;
3) 3;
4) 2.
7.
Доступно ли Вам излагается материал?
1) Доступно;
2) Ничего не понятно;
3) Другой ответ-----------------------------------____________________________________________________________________________________
8.
Как часто учитель дает задания для самостоятельного изучения?
1) Часто;
2) Иногда;
3) Никогда.
9.
Как часто учитель дает на уроках индивидуальные задания?
1) Всегда;
2) Иногда;
3) Никогда.
10.
Нравится ли Вам решать задания повышенной сложности?
1) Да;
2) Нет;
3) Даже не пытаюсь.
11.
Хотели бы Вы изучать математику углубленно?
1) Да;
2) Нет;
3) Другой ответ____________________________________________________
12.
Часто ли Вы на уроках математики решаете задачи с практическим приложением?
1) На каждом уроке;
2) Иногда;
3) Никогда не решали.
13.
Как часто Вы выполняете творческие задания?
1) Да;
2) Нет.
14.
Часто ли Вы решаете проблемные задания на уроках математики?
1) Часто;
2) Всегда;
3) Никогда;
4) Иногда.
15.
Выполняете ли Вы задания, в которых есть вопрос, но нет условия и Вам необходимо его составить?
1) Да;
2) Нет;
3) Другой ответ____________________________________________________
16.
Выполняете ли Вы задания, когда есть условие и Вам необходимо поставить вопрос?
1) Да;
2) Нет;
3) Другой ответ____________________________________________________
17.
Как Вы считаете, пригодится ли математика Вам в будущем?
1) Пригодится;
2) В некоторых моментах;
3) Не пригодится;
4) Другой ответ____________________________________________________
Результаты вводного анкетирования
| № |
Ф.И. учащихся |
Вопросы анкеты |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 1 |
Ахметова А. |
Отсутствовала |
| 2 |
Безручко Н. |
3 |
2 |
1 |
для общего развит.
ЕГЭ
|
- |
2 |
1 |
2 |
3 |
2 |
2 |
2 |
2 |
4 |
1 |
1 |
1 |
| 3 |
Величко Г. |
1 |
1 |
1 |
ВУЗ |
2 |
2 |
1 |
1 |
2 |
1 |
1 |
2 |
2 |
3 |
1 |
1 |
1 |
| 4 |
Глушков С. |
1 |
1 |
1 |
ЕГЭ, ВУЗ |
2 |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
1 |
иногда |
иногда |
2 |
| 5 |
Гут Т. |
3 |
2 |
1 |
ВУЗ |
2 |
2 |
1 |
2 |
2 |
2 |
если было обязат |
2 |
2 |
1 |
2 |
1 |
1 |
| 6 |
Ефтин А. |
Отсутствовал |
| 7 |
Казакова А. |
Отсутствовала |
| 8 |
Колпаков А. |
1 |
2 |
1 |
хорошее образов.
ВУЗ
|
1 |
2 |
бывает легко, бывает сложно |
1 |
3 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
| 9 |
Кутузов Д. |
1 |
- |
1 |
ВУЗ |
- |
- |
- |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 10 |
Кучменко А. |
1 |
1 |
1 |
получить больше знаний
ВУЗ
|
2 |
1 |
1 |
1 |
3 |
2 |
1 |
2 |
2 |
4 |
2 |
2 |
1 |
| 11 |
Лашкевич О. |
1 |
1 |
1 |
ЕГЭ, ВУЗ |
2, 4 |
1 |
периодич. не понятно |
2 |
3 |
1 |
возможно |
2 |
2 |
1 |
иногда |
2 |
в зависимот профес. |
| 12 |
Майстер М. |
Отсутствовала |
| 13 |
Макаревич О. |
1 |
2 |
1 |
изучать углубл.
ВУЗ
|
5 |
2 |
1 |
2 |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
| 14 |
Максимов Д. |
1 |
1 |
1 |
ЕГЭ, ВУЗ |
- |
2 |
1 |
1 |
3 |
1 |
2 |
2 |
2 |
1 |
2 |
2 |
1 |
| 15 |
Миришова З. |
1 |
2 |
1 |
ВУЗ |
4 |
3 |
1 |
1 |
3 |
2 |
2 |
2 |
2 |
1 |
2 |
2 |
2 |
| 16 |
Пасечник А. |
1 |
1 |
1 |
ЕГЭ |
2 |
1 |
1 |
2 |
2 |
1 |
- |
2 |
2 |
2 |
1 |
1 |
2 |
| 17 |
Романова К. |
1 |
1 |
1 |
повыш. знаний |
2 |
2 |
1 |
1 |
2 |
2 |
можно но не на каждом уроке |
2 |
2 |
1 |
2 |
иногда |
1 |
| 18 |
Секриеру С. |
1 |
2 |
когда как |
2 |
2 |
когда как |
2 |
2 |
2 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
| 19 |
Спиридонов А. |
3 |
2 |
1 |
ЕГЭ, ВУЗ |
4 |
2 |
когда понятно, когда нет |
2 |
2 |
1 |
не знаю |
2 |
1 |
4 |
1 |
1 |
1 |
| 20 |
Султанова М. |
3 |
2 |
я не понимаю ее |
нет цели |
2 |
4 |
1 |
1 |
2 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
| 21 |
Федин С. |
1 |
1 |
1 |
общего познания и развития
ВУЗ
|
2 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
| 22 |
Федоренко А. |
1 |
1 |
1 |
- |
4 |
2 |
1 |
1 |
2 |
1 |
1 |
2 |
1 |
4 |
1 |
1 |
2 |
| 23 |
Фомина А. |
1 |
2 |
1 |
ЕГЭ, ВУЗ |
1 |
2 |
многие темы не понятны |
2 |
3 |
2 |
возможно |
3 |
2 |
1 |
боюсь трогать |
2 |
1 |
| 24 |
Хабибуллина А. |
1 |
2 |
1 |
ЕГЭ, ВУЗ |
2 |
3 |
когда понятно, когда нет |
2 |
2 |
- |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
| 25 |
Чернов Д. |
3 |
2 |
2 |
чтобы хоть что-то знать |
4 |
3 |
когда понятно, когда нет |
1 |
2 |
2 |
и да, и нет |
2 |
2 |
3 |
1 |
2 |
2 |
| 26 |
Чобанзаде А. |
3 |
2 |
2 |
ЕГЭ, ВУЗ |
2, 4 |
3 |
2 |
2 |
3 |
2 |
2 |
2 |
2 |
1 |
иногда |
2 |
2 |
| 27 |
Юланова И. |
1 |
1 |
1 |
интерес
ВУЗ
|
2 |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
4 |
1 |
1 |
1 |
Вариативный ряд, составленный при статистической обработке материала вводного контроля по теме «Преобразования тригонометрических выражений» на диагностирующем этапе
| № |
Ф.И. учащихся |
Отметка |
Уровень сформированности познавательного интереса |
| 1 |
Ахметова А. |
3 |
II |
| 2 |
Безручко Н. |
3 |
II |
| 3 |
Величко Г. |
4 |
III |
| 4 |
Глушков С. |
4 |
III |
| 5 |
Гут Т. |
4 |
III |
| 6 |
Ефтин А. |
3 |
II |
| 7 |
Казакова А. |
3 |
II |
| 8 |
Колпаков А. |
2 |
I |
| 9 |
Кутузов Д. |
3 |
II |
| 10 |
Кучменко А. |
4 |
III |
| 11 |
Лашкевич О. |
4 |
III |
| 12 |
Майстер М. |
3 |
II |
| 13 |
Макаревич О. |
5 |
IV |
| 14 |
Максимов Д. |
2 |
I |
| 15 |
Миришова З. |
3 |
II |
| 16 |
Пасечник А. |
5 |
IV |
| 17 |
Романова К. |
2 |
I |
| 18 |
Секриеру С. |
3 |
II |
| 19 |
Спиридонов А. |
2 |
I |
| 20 |
Султанова М. |
2 |
I |
| 21 |
Федин С. |
5 |
IV |
| 22 |
Федоренко А. |
3 |
II |
| 23 |
Фомина А. |
3 |
II |
| 24 |
Чернов Д. |
2 |
I |
| 25 |
Чобанзаде А. |
2 |
I |
| 26 |
Юланова И. |
4 |
III |
Вариативный ряд, составленный при статистической обработке материала промежуточного контроля по теме «Преобразования тригонометрических выражений» на формирующем этапе
| № |
Ф.И. учащихся |
Отметка |
Уровень сформированности познавательного интереса |
| 1 |
Безручко Н. |
4 |
III |
| 2 |
Величко Г. |
3 |
II |
| 3 |
Глушков С. |
4 |
III |
| 4 |
Гут Т. |
4 |
III |
| 5 |
Кутузов Д. |
5 |
IV |
| 6 |
Кучменко А. |
5 |
IV |
| 7 |
Лашкевич О. |
4 |
III |
| 8 |
Макаревич О. |
4 |
III |
| 9 |
Пасечник А. |
5 |
IV |
| 10 |
Спиридонов А. |
4 |
III |
| 11 |
Федин С. |
5 |
IV |
| 12 |
Федоренко А. |
4 |
III |
| 13 |
Фомина А. |
4 |
III |
| 14 |
Юланова И. |
4 |
III |
Вариативный ряд, составленный при статистической обработке материала итогового контроля по теме «Преобразования тригонометрических выражений» на итоговом диагностирующем этапе
| № |
Ф.И. учащихся |
Отметка |
Уровень сформированности познавательного интереса |
| 1 |
Ахметова А. |
3 |
II |
| 2 |
Безручко Н. |
4 |
III |
| 3 |
Величко Г. |
4 |
III |
| 4 |
Глушков С. |
5 |
IV |
| 5 |
Гут Т. |
4 |
III |
| 6 |
Ефтин А. |
3 |
II |
| 7 |
Казакова А. |
2 |
I |
| 8 |
Колпаков А. |
3 |
II |
| 9 |
Кутузов Д. |
4 |
III |
| 10 |
Кучменко А. |
4 |
III |
| 11 |
Лашкевич О. |
4 |
III |
| 12 |
Майстер М. |
4 |
III |
| 13 |
Макаревич О. |
4 |
III |
| 14 |
Максимов Д. |
4 |
III |
| 15 |
Миришова З. |
3 |
II |
| 16 |
Пасечник А. |
5 |
IV |
| 17 |
Романова К. |
4 |
III |
| 18 |
Секриеру С. |
3 |
II |
| 19 |
Спиридонов А. |
3 |
II |
| 20 |
Султанова М. |
3 |
II |
| 21 |
Федин С. |
4 |
III |
| 22 |
Федоренко А. |
3 |
II |
| 23 |
Фомина А. |
5 |
IV |
| 24 |
Хабибуллина А. |
3 |
II |
| 25 |
Чернов Д. |
4 |
III |
| 26 |
Чобанзаде А. |
3 |
II |
| 27 |
Юланова И. |
5 |
IV |
Анкета для учащихся.
1.
Как Вы относитесь к математике?
1) Положительно;
2) Отрицательно;
3) Нейтрально.
2.
Как Вам дается изучение математики?
1) Легко;
2) Сложно;
3) Вообще не дается.
3.
Интересна ли Вам математика?
1) Интересна;
2) Не интересна;
3) Другой ответ____________________________________________________
4.
С какой целью Вы изучаете математику?________________________
________________________________________________________________
5.
Какими проблемными методами на уроках математики Вам излагается материал?
1) Проблемное изложение;
2) Исследованием;
3) Творческим обучением;
4) Поисковым или частично-поисковым методом;
5) Другой ответ____________________________________________________
6.
На какую оценку Вы оцениваете свои знания по математике?
1) 5;
2) 4;
3) 3;
4) 2.
7.
Доступно ли Вам излагается материал?
1) Доступно;
2) Ничего не понятно;
3) Другой ответ-----------------------------------____________________________________________________________________________________
8.
Как часто учитель дает задания для самостоятельного изучения?
1) Часто;
2) Иногда;
3) Никогда.
9.
Как часто учитель дает на уроках индивидуальные задания?
1) Всегда;
2) Иногда;
3) Никогда.
10.
Нравится ли Вам решать задания повышенной сложности?
1) Да;
2) Нет;
3) Даже не пытаюсь.
11.
Хотели бы Вы изучать математику углубленно?
1) Да;
2) Нет;
3) Другой ответ____________________________________________________
12.
Часто ли Вы на уроках математики решаете задачи с практическим приложением?
1) На каждом уроке;
2) Иногда;
3) Никогда не решали.
13.
Часто ли Вы выполняете творческие задания?
1) Да;
2) Нет.
14.
Часто ли Вы решаете проблемные задания на уроках математики?
1) Часто;
2) Всегда;
3) Никогда;
4) Иногда.
15.
Выполняете ли Вы задания, в которых есть вопрос, но нет условия и Вам необходимо его составить?
1) Да;
2) Нет;
3) Другой ответ____________________________________________________
16.
Вызывают ли у Вас интерес такие задания?
1) Да;
2) Нет;
3) Другой ответ____________________________________________________
17.
Выполняете ли Вы задания, когда есть условие и Вам необходимо поставить вопрос?
1) Да;
2) Нет;
3) Другой ответ____________________________________________________
18.
Вызывают ли у Вас интерес такие задания?
1) Да;
2) Нет;
3) Другой ответ____________________________________________________
19.
Как Вы считаете, пригодится ли математика Вам в будущем?
1) Пригодится;
2) В некоторых моментах;
3) Не пригодится;
4) Другой ответ____________________________________________________
Результаты итогового анкетирования
| № |
Ф.И. учащихся |
Вопросы анкеты |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| 1 |
Ахметова А. |
1 |
2 |
2 |
Надо |
2 |
2 |
1 |
2 |
2 |
3 |
2 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
2 |
| 2 |
Безручко Н. |
1 |
1 |
1 |
ЕГЭ, знания |
3 |
2 |
1 |
2 |
2 |
2 |
2 |
2 |
1 |
4 |
1 |
1 |
2 |
1 |
1 |
| 3 |
Величко Г. |
1 |
1 |
1 |
Поможет в будущем |
4 |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
4 |
2 |
1 |
1 |
1 |
1 |
| 4 |
Глушков С. |
1 |
1 |
1 |
ЕГЭ |
2 |
2 |
1 |
1 |
2 |
1 |
1 |
2 |
1 |
1 |
1 |
не очень |
1 |
иногда |
2 |
| 5 |
Гут Т. |
1 |
2 |
1 |
ВУЗ, знания |
2, 3 |
2 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
не всегда |
4 |
не всегда |
2 |
| 6 |
Ефтин А. |
1 |
2 |
1 |
ВУЗ |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
2 |
2 |
4 |
1 |
1 |
2 |
2 |
1 |
| 7 |
Казакова А. |
3 |
3 |
1 |
ЕГЭ |
2 |
4 |
2 |
2 |
2 |
3 |
2 |
2 |
2 |
2 |
бывает |
иногда |
1 |
2 |
2 |
| 8 |
Колпаков А. |
отсутствовал |
| 9 |
Кутузов Д. |
1 |
- |
1 |
ВУЗ |
2 |
- |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
| 10 |
Кучменко А. |
1 |
2 |
1 |
ВУЗ |
1 |
1 |
1 |
1 |
3 |
2 |
1 |
3 |
2 |
4 |
1 |
2 |
1 |
2 |
1 |
| 11 |
Лашкевич О. |
отсутствовала |
| 12 |
Майстер М. |
отсутствовала |
| 13 |
Макаревич О. |
1 |
2 |
1 |
Надо |
3 |
2 |
1 |
2 |
1 |
1 |
1 |
2 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
| 14 |
Максимов Д. |
1 |
1 |
1 |
ЕГЭ |
3 |
2 |
1 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
| 15 |
Миришова З. |
1 |
2 |
1 |
ВУЗ |
1 |
3 |
1 |
1 |
2 |
2 |
1 |
2 |
2 |
4 |
1 |
2 |
1 |
2 |
1 |
| 16 |
Пасечник А. |
1 |
1 |
1 |
ЕГЭ |
2 |
1 |
1 |
3 |
2 |
1 |
не очен |
2 |
2 |
4 |
иногда |
не всегда |
1 |
2 |
2 |
| 17 |
Романова К. |
1 |
1 |
1 |
ЕГЭ, знания |
1, 2, 3 |
2 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 18 |
Секриеру С. |
отсутствовала |
| 19 |
Спиридонов А. |
1 |
2 |
1 |
ЕГЭ, нужна для информатики |
1, 3 |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
1 |
Не всегда |
1 |
1 |
1 |
1 |
| 20 |
Султанова М. |
3 |
2 |
2 |
не знаю |
1, 2 |
4 |
2 |
1 |
2 |
3 |
2 |
2 |
2 |
1 |
редко |
2 |
не знаю |
2 |
1 |
| 21 |
Федин С. |
1 |
1 |
1 |
общее развитие и проф. |
1, 2, 3, 4 |
1 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| 22 |
Федоренко А. |
1 |
1 |
1 |
- |
- |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
1 |
3 |
1 |
1 |
1 |
1 |
3 |
| 23 |
Фомина А. |
1 |
2 |
1 |
пригодится в будущем |
2 |
2 |
1 |
3 |
2 |
1 |
возм |
2 |
2 |
1 |
1 |
иногда |
2 |
1 |
1 |
| 24 |
Хабибуллина А. |
1 |
2 |
1 |
ВУЗ |
2 |
3 |
1 |
1 |
1 |
1 |
Несовсем |
2 |
2 |
1 |
1 |
1 |
иногда |
1 |
1 |
| 25 |
Чернов Д. |
3 |
2 |
1 |
4 |
3 |
1 |
1 |
1 |
2 |
1 |
2 |
2 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
| 26 |
Чобанзаде А. |
3 |
2 |
2 |
- |
1, 2 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
- |
4 |
2 |
2 |
2 |
2 |
2 |
| 27 |
Юланова И. |
отсутствовала |
Решение вводной самостоятельной работы.
Вариант 1.
1. Упростите выражение:
 . .
2. Вычислите:
 . .
3. Решите уравнения:
а) 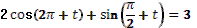 ; ;
;
;
 ; ;
 . .
Ответ: . .
б)  ; ;
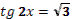 ; ;
 ; ;
;
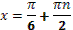 . .
Ответ: . .
4. Доказать тождество:
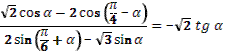 ; ;
 ; ;
 ; ;
 ; ;
 ; ;
 . .
Вариант 2.
1. Упростите выражение:
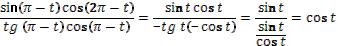 . .
2. Вычислите:
 . .
3. Решите уравнения:
а)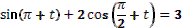 ; ;
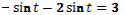 ; ;
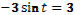 ; ;
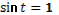 ; ;
 . .
Ответ:.
б) 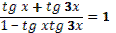 ; ;
 ; ;
;
;
 . .
Ответ: . .
4. Доказать тождество:
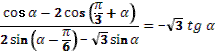 ; ;
 ; ;
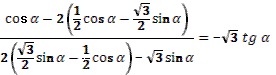 ; ;
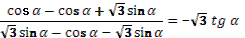 ; ;
 ; ;
 . .
Решение самостоятельной работы на тему «Формулы двойного аргумента».
Вариант 1.
1. Вычислите:
 . .
2. Упростите выражение:
 . .
3. Решите уравнения:
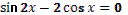 ; ;
;
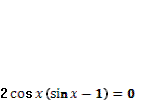 ; ;
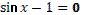
 
 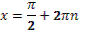
Ответ:, 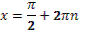 . .
4. Доказать тождество:
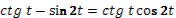 ; ;
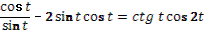 ; ;
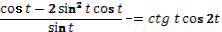 ; ;
 ; ;
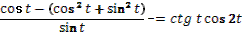 ; ;
 . .
5*. Даны корни уравнения  и и 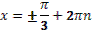 . .
 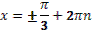
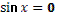 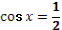
 ; ;
;
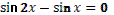 . .
Вариант 2.
1. Вычислите:
.
2. Упростите выражение:
 . .
3. Решите уравнения:
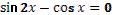 ; ;
;
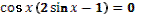 ; ;




Ответ:, 
4. Доказать тождество:
 ; ;
;
 ; ;
 ; ;
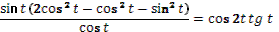 ; ;
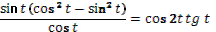 ; ;
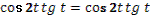 . .
5*. Даны корни уравнения  и и  . .
 

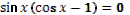 ; ;
 ; ;
;
 . .
Решение самостоятельной работы по теме «Формулы понижения степени».
Вариант 1.
1. Решите уравнение:
 ; ;
;
;
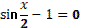
 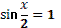
 
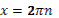 
Ответ: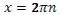 , , 
2. Докажите тождество:
;
;
 ; ;
 ; ;
 . .
3. Известно, что 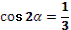 . Вычислите . Вычислите 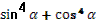 . .
 . .
4*. Дан корень уравнения 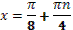 . .
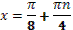 ; ;
;
 ; ;
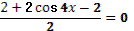 ; ;
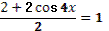 ; ;
;
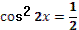 . .
Вариант 2.
1. Решите уравнение:
;
;
;

 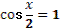
 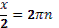
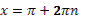 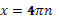
Ответ: , , 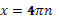
2. Докажите тождество:
;
;
 ; ;
 ; ;
 . .
3. Известно, что  . Вычислите . Вычислите 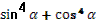 . .
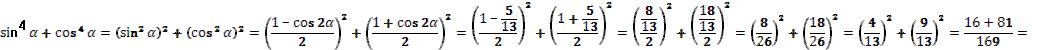 . .
4*. Дан корень уравнения 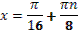 . .
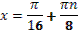 ; ;
;
 ; ;
 ; ;
 ; ;
;
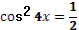 . .
Решение самостоятельной работы по теме «Преобразование произведения тригонометрических функций в сумму».
Вариант 1.
1. Представьте в виде суммы:
 . .
2. Вычислите:
.
3. Решите уравнение:
 ; ;
 ; ;
 ; ;
;
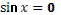 . .
 . .
Ответ: . .
4*. Дано равенство 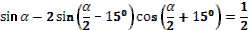 . Сформулируйте и запишите задание и решите его. . Сформулируйте и запишите задание и решите его.
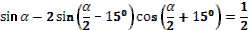 ; ;
Доказать тождество.
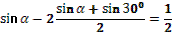 ; ;
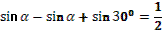 ; ;
 . .
Вариант 2.
1. Представьте в виде суммы:
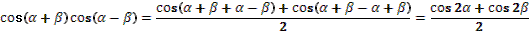 . .
2. Вычислите:
.
3. Решите уравнения:
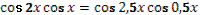 . .
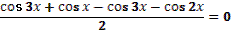 ; ;
 ; ;
 ; ;
 ; ;
;
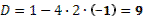 ; ;
 ; ;
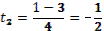 ; ;


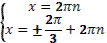
Ответ: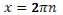 , ,  . .
4*. Дано равенство 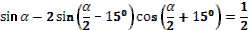 . Сформулируйте и запишите задание и решите его. . Сформулируйте и запишите задание и решите его.
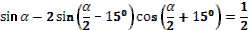 ; ;
Доказать тождество.
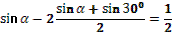 ; ;
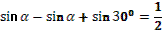 ; ;
 . .
Решение итоговой контрольной работы на тему «Преобразования тригонометрических выражений».
Вариант 1.
Часть А.
1. Упростите выражение
 . .
а)  ; б) ; б) 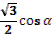 ; в) ; в) 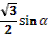 ; г) ; г) 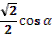 . .
Ответ: б.
2. Вычислите
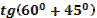 . .
а) 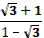 ; б) ; б)  ; в) ; в) 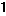 ; г) ; г)  . .
Ответ: а.
3. Упростите выражение
 . .
а) 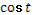 ; б) ; б) 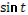 ; в) ; в) 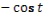 ; г) ; г) 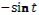 . .
Ответ: а.
4. Упростите выражение
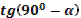 . .
а) 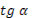 ; б) ; б)  ; в) ; в) 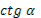 ; г) ; г) 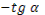 . .
Ответ: в.
5. Вычислите
 . .
а) 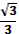 ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
Ответ: г.
6. Вычислите
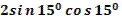 . .
а) 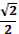 ; б) ; б) 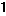 ; в) ; в)  ; г) ; г) 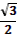 . .
Ответ: в.
Часть В.
1.
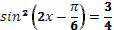 . Сформулируйте задание и решите его. . Сформулируйте задание и решите его.
 ; ;
;
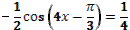 ; ;
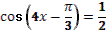 ; ;
;
;


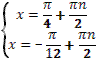
Ответ: 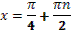 , , 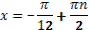 . .
2.
Представьте в виде произведения 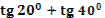 . .
 . .
Часть С.
1.
Дан корень уравнения 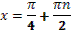 . .


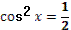
2.
Дано равенство 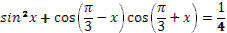 . Сформулируйте и запишите задание и решите его. . Сформулируйте и запишите задание и решите его.
Доказать тождество.
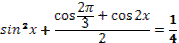
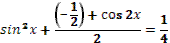
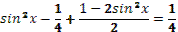
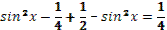

 . .
Вариант 2.
Часть А.
1. Упростите выражение
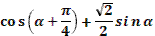 . .
а)  ; б) ; б) 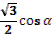 ; в) ; в) 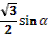 ; г) ; г) 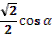 . .
Ответ: г.
2. Вычислите
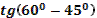 . .
а) 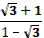 ; б) ; б) 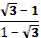 ; в) ; в) 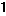 ; г) ; г)  . .
Ответ: б.
3. Упростите выражение
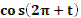 . .
а) 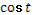 ; б) ; б) 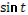 ; в) ; в) 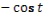 ; г) ; г) 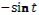 . .
Ответ: а.
4. Упростите выражение
 . .
а) 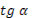 ; б) ; б)  ; в) ; в) 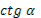 ; г) ; г) 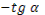 . .
Ответ: в.
5. Вычислите
 . .
а) 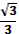 ; б) ; б)  ; в) ; в)  ; г) ; г)  . .
Ответ: б.
6. Вычислите
 . .
а) 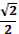 ; б) ; б) 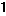 ; в) ; в)  ; г) ; г) 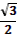 . .
Ответ: г.
Часть В.
1.
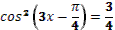 .
Сформулируйте задание и решите его. .
Сформулируйте задание и решите его.
 ; ;
;
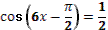 ; ;
;
;
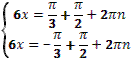
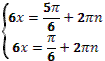

Ответ:  , , 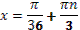 . .
2.
Представьте в виде произведения 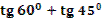 . .
 . .
Часть С.
1
.
Дан корень уравнения 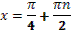 . .


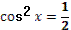
2.
Дано равенство . Сформулируйте и запишите задание и решите его.
Доказать тождество.
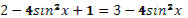

|