ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МОСКОВСКИЙ ГОСУДАРСТВЕНЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ
имени М.А. Шолохова
Факультет информатики и математики
Кафедра высшей математики
Курсовая работа по теме:
«Элементы векторного анализа»
Выполнила:
студентка IV курса группы ФИМ-М-1402
очного отделения
специальность «математика»
Шакурова Н.Н.
Проверила:
доцент Дорошкевич О.А.
Москва 2008
ОГЛАВЛЕНИЕ
Введение
Глава I. Криволинейные и поверхностные интегралы
§1. Криволинейный интеграл I рода
§2. Криволинейный интеграл II рода
§3. Поверхностный интеграл I рода
§4. Поверхностный интеграл II рода
§5. Формулы Грина, Остроградского-Гаусса, Стокса
Глава II. Теория поля
§1. Основные понятия теории поля
§2. Скалярное поле
Производная скалярного поля по направлению
Градиент скалярного поля
§3. Векторное поле и его циркуляция
Поток векторного поля
Дивергенция векторного поля. Формула Остроградского–Гаусса в векторной форме
Вихревой вектор поля. Формула Стокса в векторной форме
§4. Специальные векторные поля
§5. Оператор Лапласа. Гармонические функции
Глава III. Практическая часть.
Заключение
Список литературы
ВВЕДЕНИЕ
Для описания физической реальности математикам стало не доставать основных типов чисел (целые, рациональные, иррациональные, комплексные, …). Чтобы иметь возможность для некоторых величин указывать не только их числовое значение, но и направление, было введено понятие вектора как направленного отрезка. Следовательно, вектор – абстракция математических объектов, характеризующихся модулем и направлением. Примерами физических векторных величин являются перемещение, скорость, ускорение, напряженность электрического ил магнитного поля.
Сам термин «вектор» (от лат. vector – несущий) впервые появился у Гамильтона в 1845г. В работах по построению числовых систем, обобщающих комплексные числа. Гамильтону принадлежат термины «скаляр», «скалярное произведение», «векторное произведение».
После введения понятия вектора были более детально разработаны правила операций над векторами, что привело к появлению сначала векторной алгебры, а затем и векторного анализа
. Векторная алгебра изучает простейшие операции над векторами. Она стала своеобразным языком аналитической геометрии. Векторный анализ изучает векторные и скалярные поля. Основными понятиями векторного анализа являются «градиент», «дивергенция», «ротор» («вихрь») и «лапласиан».
Многие результаты векторного исчисления получены Германом Грассманом и английским математиком Уильямом Клиффордом. Окончательный вид векторная алгебра и векторный анализ приобрели в трудах американского физика и математика Джозайн Уилларда Гиббса, который в 1901г. Опубликовал обширный учебник по векторному анализу.
Следует отметить, что в ясно очерченном виде векторная алгебра появилась примерно на 30 лет позже первых работ по теории кватернионов (это числа, каждое из которых определяет величину и направление в пространстве). Гиббс показал связь векторной алгебры с теорией кватернионов и алгеброй Грассмана. Он был большим энтузиастом распространения векторного исчисления в различных областях точных наук.
Понятие вектора может быть введено аксиоматически, тогда вектор будет пониматься как элемент векторного пространства. Развитием понятия «вектор» можно считать понятие «тензор».
Тензорное исчисление — раздел математики, изучающий тензоры и тензорные поля. Тензорное исчисление разделяется на тензорную алгебру, входящую в качестве основной части в полилинейную алгебру, и тензорный анализ, изучающий дифференциальные операторы на алгебре тензорных полей. Тензорное исчисление является важной составной частью аппарата дифференциальной геометрии. В этой связи оно впервые систематически было развито Дж.Риччи и Т.Леви-Чивитой, его часто называли «исчислением Риччи».
Термин «тензор» еще с середины XIXв. употребляется в механике при описании упругих деформаций тел. С начала XX в. аппарат тензорного исчисления систематически используется в релятивистской физике.
Изучение векторного анализа сводится к изучению дифференциального и интегрального исчисления, включающего криволинейные и поверхностные интегралы, их основные свойства и понятия; а также теорию поля, которая является обобщением основных понятий векторного анализа.
Теория поля – крупный раздел физики, механики, математики, в котором изучаются скалярные векторные и тензорные поля. Теория поля устанавливает и исследует связи между величинами, характеризующими поле.
Следовательно, мы можем выделить основную цель нашей работы: рассмотрение важнейших операций векторного анализа — градиента, ротора, циркуляции и дивергенции, а также наиболее важных теорем векторного анализа — формулы Грина, теоремы Стокса, формулы Остроградского-Гаусса.
Ученые, занимавшиеся исследованием векторного анализа:
ГАМИЛЬТОН Уильям Роуан (Hamilton William Rowan)
Гамильтон Уильям Роуан (04.08.1805-02.09.1865)-ирландский математик, член Ирландской Академии Наук. Родился в Дублине. К 17 годам он изучил "Начала" Евклида, а также сочинения И. Ньютона и П.Лапласа. Окончил Тринити – колледж Дублинского университета, в 22 года стал профессором астрономии в Дублинском университете и директором университетской астрономической обсерватории. Основные труды по механике и теории дифференциальных уравнений (Гамильтона-Остроградского-Якоби уравнение) и функциональному анализу, где важную роль играет оператор Гамильтона («набла»). Открыл вариационный принцип в механике, который был обобщен М.В.Остроградским. Гамильтон почти одновременно с немецким математиком Г. Грассманом дал точное формальное изложение теории комплексных чисел как частного случая числовых систем с несколькими единицами. Построил своеобразную систему чисел (кватернионов). Над теорией кватернионов Гамильтон трудился 8 лет. Это учение в дальнейшем было одним из источников развития векторного анализа. Гамильтон ввел термины "вектор", "ассоциативный закон". Известны работы Гамильтона в геометрии (где он занимался теорией волновых поверхностей) и алгебре. Гамильтон и Кэли разработали теорию матриц.
ГРАССМАН Герман Гюнтер (Grassmann Hermann Günter)
Грассман Герман Гюнтер (15.04.1809—26.09.1877) – немецкий математик, занимавшийся также физикой и филологией. Родился в Штеттине. C 1842 работал в Штеттинской гимназии. В сочинении "Учение о линейном протяжении" ("Lineale Ausdehnungslehre", Lpz., 1844) дал первое систематическое построение учения о многомерном евклидовом пространстве, способствовавшее развитию векторного и тензорного исчислений. Однако из-за абстрактного изложения и необычайной терминологии сочинение было малодоступным. В области физики Грассману принадлежат работы по акустике и магнитному взаимодействию токов. Общие идеи Грассмана об абстрактных векторных пространствах привели его к открытию важного положения - возможности рассматривать цветовые ощущения как трехмерные векторы, что лежит в основе современного учения о цвете. Им установлены (1853) законы сложения цветов. Грассман составил (1875) полный словарь к гимнам Ригведы (памятнику древнеиндийской литературы).
ГИББС Джозайя Уиллард (Gibbs, Josiah Willard)
Американский физик и математик Гиббс Джозайя Уиллард (11.02.1839–28.04.1903) родился в Нью-Хейвене, штат Коннектикут. Он окончил Йельский университет, где его успехи в греческом, латыни и математике были отмечены призами и премиями. В 1863 г. Гиббс получил степень доктора философии и стал преподавателем университета; первые два года преподавал латынь и лишь затем – математику. В 1866–1869 гг. Гиббс продолжил образование в Сорбонне и Коллеж де Франс в Париже, в Берлинском и Гейдельбергском университетах. После возвращения в Нью-Хейвен возглавил кафедру математической физики Йельского университета и занимал её до конца жизни.
Разработал теорию термодинамических потенциалов, открыл общее условие равновесия гетерогенных систем правило фаз, вывел уравнения Гиббса Гельмгольца, Гиббса Дюгема, адсорбционное уравнение Гиббса. Установил фундаментальный закон статистической физики распределение Гиббса. Предложил графическое изображение состояния трехкомпонентной системы (треугольник Гиббса). Заложил основы термодинамики поверхностных явлений и электрохимических процессов. Ввел понятие адсорбции. Является также одним из создателей векторного исчисления в его современной форме ("Элементы векторного анализа", 1881- 1884).
ОСТРОГРАДСКИЙ Михаил Васильевич
Михаил Васильевич Остроградский (12.11.1801–20.12.1861) — российский и украинский математик и механик, признанный лидер математиков Российской империи середины XIX века. Родился в деревне Пашенная Полтавской губернии, в семье помещика. Получил первоначальное образование в пансионе при полтавской гимназии. Окончил курс математического факультета в Харьковском университете; затем посещал в Париже лекции в Сорбонне и в College de France. Здесь он обратил на себя внимание знаменитых математиков Лапласа, Фурье, Ампера, Пуассона, Коши. По возвращении из Санкт-Петербурга он в 1828 г. избран был адъюнктом Академии Наук, через два года - ординарным академиком. Преподавал в офицерских классах морского корпуса, в институте инженеров путей сообщения, в главном педагогическом институте, в училищах инженерном и артиллерийском. В военно-учебных заведениях он был главным наблюдателем преподавания по математическим наукам. Основные работы Остроградского относятся к прикладным аспектам математического анализа, механики, теории упругости и магнетизма, теории вероятностей. Он внёс также вклад в алгебру и теорию чисел. Хорошо известен метод Остроградского для интегрированиярациональных функций (1844). В физике чрезвычайно полезна формула Остроградского для преобразования объёмного интеграла в поверхностный. В последние годы жизни Остроградский опубликовал исследования по интегрированию уравнений динамики.
Глава I. Криволинейные и поверхностные интегралы
§1. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ I РОДА
 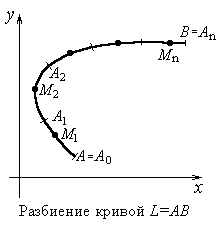 Пусть на плоскости Oxy
задана непрерывная кривая L
= АВ
длиныl
. Рассмотрим непрерывную функцию f
(x
; y
), определенную в точках дуги L
.
Разобьем кривуюL
последовательными точками Пусть на плоскости Oxy
задана непрерывная кривая L
= АВ
длиныl
. Рассмотрим непрерывную функцию f
(x
; y
), определенную в точках дуги L
.
Разобьем кривуюL
последовательными точками
А
0
=А
, А
1
, А
2
, . . . , А
n
=В
на n
дуг
d
1
= А
0
А
1
,d
2
= А
1
А
2
, . . . ,d
n
= А
n
-1
А
n
.
На дуге d
i
выберем произвольную точку М
i
(ti
;si
) (i
= 1,2, . . . , n
) (рис. 1). Обозначим Dli
длину дуги d
i
, а
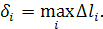
Составим интегральную сумму
функции f
(x
,y
) по кривой L:

Определение.
Предел 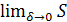 , если он существует, называется криволинейным интегралом I
рода
от функции f
(x
; y
) по кривой L
и обозначается , если он существует, называется криволинейным интегралом I
рода
от функции f
(x
; y
) по кривой L
и обозначается

В случае замкнутой кривой L
криволинейный интеграл I рода определяется аналогично случаю незамкнутой кривой.
Основные свойства криволинейного интеграла I рода
:
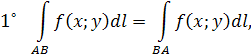
т.е. криволинейный интеграл I рода не зависит от направления пути интегрирования.
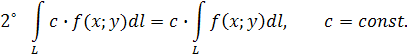
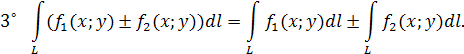
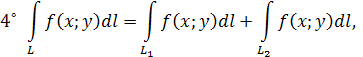
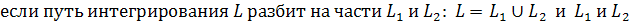
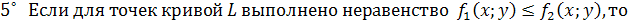

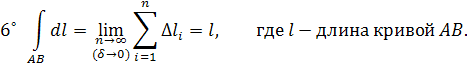
7˚ Если функцияf
(
x
;
y
)
непрерывна на кривой АВ
, то на этой кривой найдетсяточка (
xc
;
yc
):
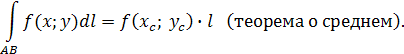
Вычисление криволинейного интеграла 1-го рода
Пусть кривая L
задана параметрическими уравнениями:
x
=
x
(t
), y
=
y
(t
), a
≤ t
≤b
, где x
(t
), y
(t
) - непрерывно дифференцируемые функции на отрезке [a
,b
] функции. Тогда
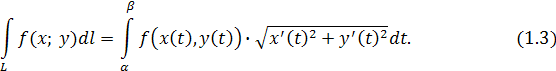
Пусть кривая L
задана явно
уравнением:
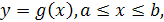
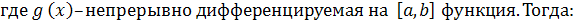
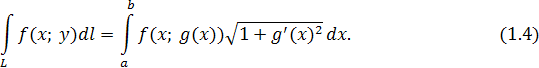
Пусть кривая L
задана в полярных координатах
:
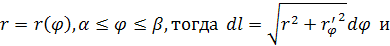
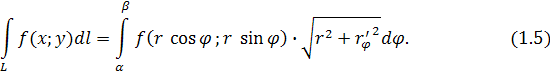
Геометрические приложения
- Длина кривой АВ вычисляется по формуле

- Площадь цилиндрической поверхностиz
=
f
(
x
;
y
)
с направляющей АВ
и образующей,
параллельной Oz
,
находится

- Масса материальной кривой АВ
определяется формулой

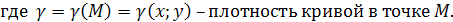
- Статистические моменты и координаты центра тяжести кривой АВ
определяются по формулам
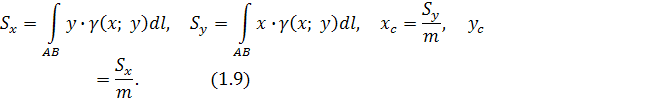
- Для кривой АВ
моменты инерции относительно осей Ox
,
Oy
и начала координат равны:
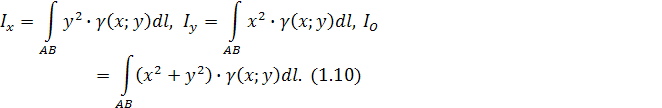
§2.
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ II РОДА
 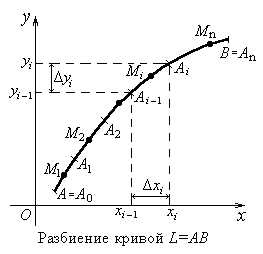 Пусть на плоскости Oxy
задана непрерывная кривая L
= АВ
и функцияP
(
x
;
y
),
определенная в каждой точке кривой. Разобьем кривуюL
последовательными точками А
0
=А
, А
1
, А
2
, . . ., А
n
=В
в направлении от точки А
к точке В
на n
дуг d
i
= Пусть на плоскости Oxy
задана непрерывная кривая L
= АВ
и функцияP
(
x
;
y
),
определенная в каждой точке кривой. Разобьем кривуюL
последовательными точками А
0
=А
, А
1
, А
2
, . . ., А
n
=В
в направлении от точки А
к точке В
на n
дуг d
i
=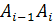 с длинами с длинами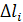 (i
= 1,2, . . . , n
). На каждой элементарной дуге d
i
возьмем точку ( (i
= 1,2, . . . , n
). На каждой элементарной дуге d
i
возьмем точку (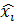 ; ; 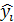 ) и составим сумму вида: ) и составим сумму вида:
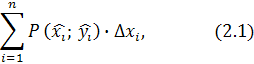
где 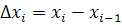 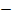 проекция дуги d
i
на ось Ox
(рис.2). проекция дуги d
i
на ось Ox
(рис.2).
|
Определение.
Если приδ=
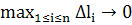 интегральная сумма (2.1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ
, ни от выбора точек ( интегральная сумма (2.1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ
, ни от выбора точек (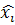 ; ; 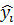 ), то его называют криволинейным интегралом по координате
x
(или II рода) от функции
P
(
x
;
y
) по кривой
L
: ), то его называют криволинейным интегралом по координате
x
(или II рода) от функции
P
(
x
;
y
) по кривой
L
:
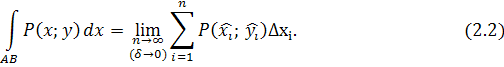
Аналогично вводится криволинейный интеграл от функции Q
(
x
;
y
)
по координате y
:
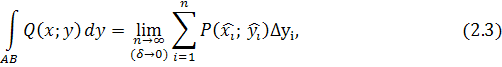
где 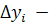 проекция дуги проекция дуги 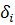 на ось Oy
. на ось Oy
.
Криволинейный интеграл II рода общего вида определяется равенством:
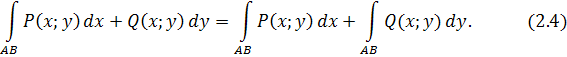
Основные свойства криволинейного интеграла II рода
1˚ При изменении направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противоположный:
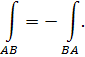
2˚ Если кривая АВ
точкой С
разбита на две части АС
и СВ
, то интеграл по всей кривой равен сумме интегралов по ее частям:
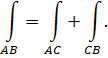
3˚ Если кривая АВ
лежит в плоскости, перпендикулярной оси Ox
, то
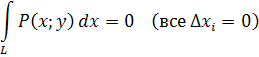
аналогично для кривой, лежащей в плоскости, перпендикулярной оси Oy
:
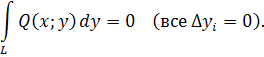
4˚ Криволинейный интеграл по замкнутой кривой (обозначается 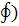
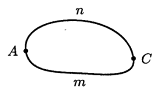 не зависит от выбора начальной точки (зависит только от направления обхода кривой). не зависит от выбора начальной точки (зависит только от направления обхода кривой).
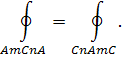
Вычисление криволинейного интеграла 1-го рода
Пусть кривая L
задана параметрическими уравнениями:
x
=
x
(t
), y
=
y
(t
), a
≤ t
≤b
, где x
(t
), y
(t
) - непрерывно дифференцируемые функции на отрезке [a
,b
] функции. Тогда
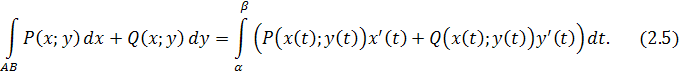
Пусть кривая L
задана явно
уравнением:
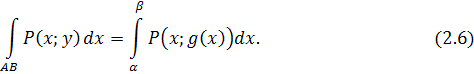
Геометрические приложения
- Площадь S
плоской фигуры, расположенной в плоскости Oxy
и ограниченной замкнутой линией L
, можно найти по формуле

при этом кривая L
обходится против часовой стрелки.
- Переменная сила на участке АВ равна

Условия независимости криволинейного интеграла II рода от пути интегрирования
Для того чтобы криволинейный интеграл
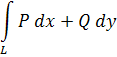
не зависел от пути интегрирования в односвязной области в (область без «дыр»), в которой существуют и непрерывны 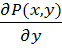 и и 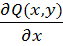 необходимо и достаточно, чтобы необходимо и достаточно, чтобы

Замечание.
Криволинейные интегралыI и II рода связаны соотношением
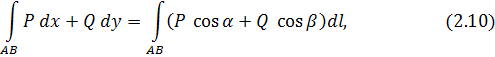
где 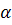 и и 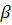 – углы, образованные касательной к кривой АВ
в точке M
(
x
;
y
)
с осями Ox
и Oy
. – углы, образованные касательной к кривой АВ
в точке M
(
x
;
y
)
с осями Ox
и Oy
.
§3. ПОВЕРХНОСТНЫЙ
ИНТЕГРАЛ I РОДА
 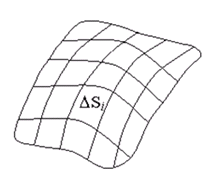 Пусть S
- поверхность в трёхмерном пространстве Oxyz
, а f
(x; y; z)
- непрерывная функция, определённая в точках этой поверхности. Поверхность S
сетью линий разобьём на n
участков ΔS1
,
ΔS2
, ...., ΔSi
, ..., ΔSn
, не имеющих общих внутренних точек (рис. 3). Площади "элементарных" участков обозначим теми же буквами Si
(i = 1,...,n)
, а наибольший из диаметров этих участков - через λ
На каждом "элементарном" участке ΔSi
произвольным образом выберем по точке Mi
(xi
; yi
; zi
) (i = 1,...,n)
и составим интегральную сумму: Пусть S
- поверхность в трёхмерном пространстве Oxyz
, а f
(x; y; z)
- непрерывная функция, определённая в точках этой поверхности. Поверхность S
сетью линий разобьём на n
участков ΔS1
,
ΔS2
, ...., ΔSi
, ..., ΔSn
, не имеющих общих внутренних точек (рис. 3). Площади "элементарных" участков обозначим теми же буквами Si
(i = 1,...,n)
, а наибольший из диаметров этих участков - через λ
На каждом "элементарном" участке ΔSi
произвольным образом выберем по точке Mi
(xi
; yi
; zi
) (i = 1,...,n)
и составим интегральную сумму:

Определение.
Если существует конечный предел

не зависящий от способа разбиения поверхности S
на "элементарные" участки ΔSi
и от выбора точек Mi
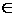 ΔSi
(i=1,....n)
, то он называется поверхностным интегралом I рода от функции ΔSi
(i=1,....n)
, то он называется поверхностным интегралом I рода от функции
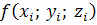 поверхности S
и обозначается поверхности S
и обозначается
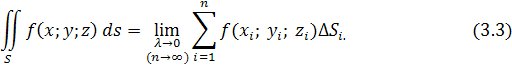
Если поверхность S
гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f
(x; y; z)
непрерывна на этой поверхности, то поверхностный интеграл существует (теорема существования).
Основные свойства криволинейного интеграла I рода:
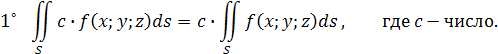
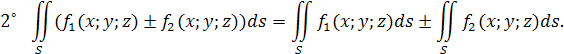
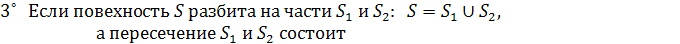 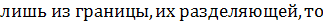
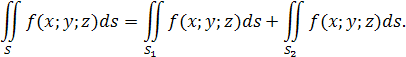

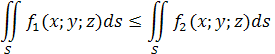
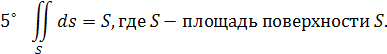
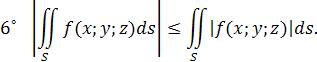
7
˚ Если 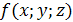 непрерывна на поверхности непрерывна на поверхности 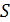 , то на этой поверхности существует точка , то на этой поверхности существует точка  (теорема о среднем значении): (теорема о среднем значении):
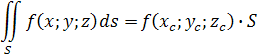
Вычисление криволинейного интеграла I рода
Вычисление поверхностных интегралов первого рода обычно производится путём их сведения к двойным интегралам.
Пусть выполнены условия теоремы существования, тогда, обозначив проекцию ΔSi
(и площадь проекции) на плоскость Oxy
через Δτi
, по теореме о среднем значении будем иметь:
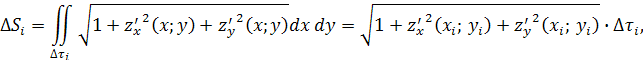
где (xi
, yi
)
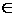 Δτi
, а, следовательно Δτi
, а, следовательно
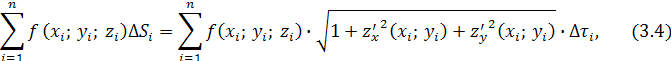
при данном специфическом выборе точек Mi
. Но сумма, стоящая справа, в последнем интеграле есть интегральная сумма для функции
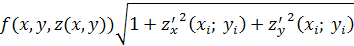
по плоской области τ
. Переходя к пределу, получаем:
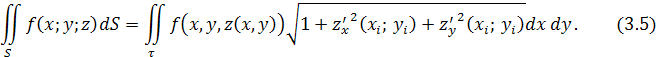
Если проектировать поверхность S
не на координатную плоскость Oxy
, а на координатную плоскость Oxz
или Oyz
, то можно записать формулы для вычисления поверхностного интеграла аналогично формуле (3.5):
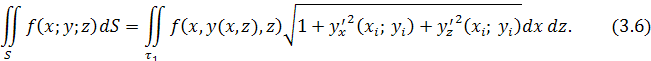
и
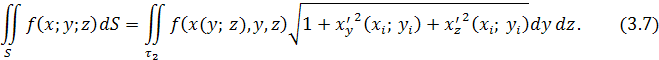
Геометрические приложения
- Площадь поверхности, заданной уравнением z
=
z
(
x
;
y
)
:
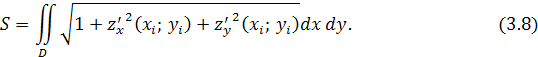
- Масса поверхностиS
:

где 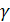 – плотность распределения массы. – плотность распределения массы.
- Моменты, центр тяжести поверхности:
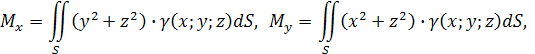
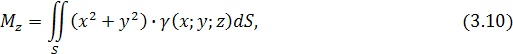
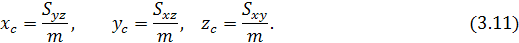
Глава II. Теория поля
§1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ПОЛЯ
Теория поля – крупный раздел, физики, механики, математики, в котором изучаются скалярные, векторные, тензорные поля.
К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин.
Полем
называется область V
пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке М
этой области соответствует определенное число U
=
U
(
M
),
говорят, что в области определено, задано скалярное поле
(или функция точки). Иначе говоря, скалярное поле – это скалярная функция U
(
M
)
вместе с ее областью определения. Если же каждой точке М
области пространства соответствует некоторый вектор 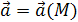 , то говорят, что задано векторное поле
(или векторная функция точки). , то говорят, что задано векторное поле
(или векторная функция точки).
Примерами скалярных полей могут быть поля температуры, атмосферного давления, плотности, электрического потенциала и т.д. Примерами векторных полей являются поле силы тяжести, поле скоростей частиц текущей жидкости (ветра), магнитное поле, поле плотности электрического тока и т.д.
Если функция U
(
M
) (
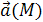 ) не зависит от времени, то скалярное (векторное) поле называется стационарным
; поле, которое меняется с течением времени называется нестационарным
. ) не зависит от времени, то скалярное (векторное) поле называется стационарным
; поле, которое меняется с течением времени называется нестационарным
.
Далее будем рассматривать только стационарные поля.
Если V
– область трехмерного пространства, то скалярное поле U
можно рассматривать как функцию трех переменных x
,
y
,
z
(координат точки M
):

Наряду с обозначениями U
=
U
(
M
),
U
=
U
(
x
;
y
;
z
),
используют запись U
=
U
(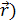 , где , где 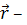 радиус-вектор точки М
.) радиус-вектор точки М
.)
Если скалярная функция U
(
M
)
зависит только от двух переменных, например x
и y
, соответствующее скалярное поле U
(
x
;
y
)
называют плоским
.
Аналогично: вектор 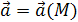 можно рассматривать как векторную функцию трех скалярных аргументов x
,
y
и z
: можно рассматривать как векторную функцию трех скалярных аргументов x
,
y
и z
:  или или 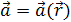 . Вектор . Вектор 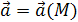 можно представить в виде можно представить в виде
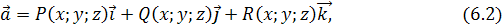
где P
(
x
;
y
;
z
),
Q
(
x
;
y
;
z
),
R
(
x
;
y
;
z
)
– проекции вектора 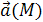 на оси координат. Если в выбранной системе координат Oxyz
одна из проекций вектора на оси координат. Если в выбранной системе координат Oxyz
одна из проекций вектора 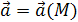 равна 0, а две другие зависят только от двух переменных, то векторное поле называется плоским
. равна 0, а две другие зависят только от двух переменных, то векторное поле называется плоским
.
Векторное поле называется однородным
, если 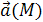 - постоянный вектор (P
, Q, R
– постоянные величины). - постоянный вектор (P
, Q, R
– постоянные величины).
В дальнейшем будем полагать, что скалярные функции: U
(
x
;
y
;
z
)
– определяющая скалярное поле, P
(
x
;
y
;
z
),
Q
(
x
;
y
;
z
),
R
(
x
;
y
;
z
)
– задающее векторное поле, непрерывны вместе со своими частными производными.
§2. СКАЛЯРНОЕ ПОЛЕ
Пусть задано скалярное стационарное поле U = f(M) = f(
x
; y; z)
, где функцию f(
x
; y; z)
будем всегда предполагать непрерывно дифференцируемой в рассматриваемой области.
Основной вопрос исследования скалярного поля есть вопрос об изменении функции U
при переходе из одной точки пространства в другую. Для выяснения этого вопроса рассмотрим, прежде всего, геометрическое место точек, в которых величина U
сохраняет постоянное значение. Это геометрическое место точек называют поверхностью уровня
скалярного поля U
. Ее уравнение в выбранной системе координат имеет вид: U(
x
; y; z) = C
, где C = const.
Следовательно, изменяя значения C, получаем семейство поверхностей уровня, которые заполняют всю область, где определено поле, и никакие две поверхности уровня, отвечающие различным значениям C, не имеют общих точек.
Задание всех поверхностей уровня с указанием соответствующих значений C
равносильно заданию самого поля. Указанный способ изображения поля особенно удобен, если речь идет о поле, заданном в плоской области D
двух переменных. В этом случае уравнение U(x,y) = C
определяет, вообще говоря, некоторую кривую линию, называемую линией уровня плоского скалярного поля
.
Такие линии различных скалярных полей всем хорошо известны: линии равных высот (горизонтали) удобны для изображения размера местности, линии равных температур (изотермы) или линии равных давлений (изобары) в метеорологии и т. д.
Производная скалярного поля по направлению
Производной скалярной функции U = f(x;,y; z) по направлению
вектора

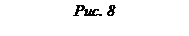  M0
(x0
; y0
; z0
)
называется предел, если он существует, отношения приращения ΔU0
функции при смещении из точки M0
(x0
; y0
; z0
)
в направлении вектора M0
(x0
; y0
; z0
)
называется предел, если он существует, отношения приращения ΔU0
функции при смещении из точки M0
(x0
; y0
; z0
)
в направлении вектора 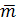 в точку M1
(x; y; z)
к величине этого смещения в точку M1
(x; y; z)
к величине этого смещения 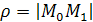 , когда ρ
→ 0, то есть , когда ρ
→ 0, то есть
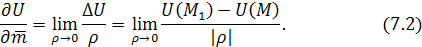
Следовательно, 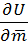 характеризует скорость изменения величины U
в точке M0
в направлении вектора характеризует скорость изменения величины U
в точке M0
в направлении вектора 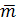 . .
Очевидно, что функция U
имеет бесчисленное множество производных по направлениям в каждой точке M
. Получим формулу для вычисления производной по направлению. Так как
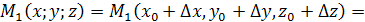
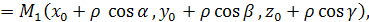
где величины x0
, y0
,z0
, cos
α
, cos
β
, cos
γ
фиксированы, то U(M1
)
есть функция только смещения ρ
Обозначим эту функцию
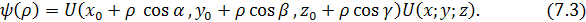
Приρ
= 0 имеемψ
(0) = U(x0
, y0
, z0
) = U(M0
)
. Следовательно:
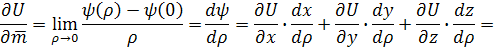
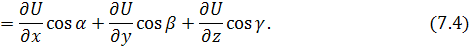
Т. е. получим формулу:
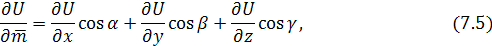
выражающую производную от функции U = f(x;,y; z)
по направлению вектора 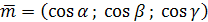
Градиент скалярного поля
Пусть задано скалярное поле U = f(x; y; z)
. Градиентом скалярного поля
U = f(x; y; z)
в точке M(x; y; z)
называют вектор
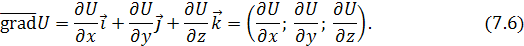
Если функция U = f(x; y; z)
имеет частные производные U'x
, U'y
, U'z
в каждой точке некоторой области, то скалярное поле порождает в этой области векторное поле 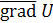 . Преобразуем формулу для вычисления производной по направлению: . Преобразуем формулу для вычисления производной по направлению:
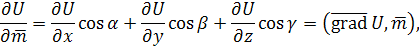
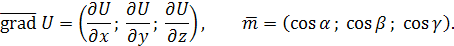
Угол между векторами 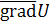 и и 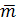 обозначим через φ
, тогда скалярное произведение обозначим через φ
, тогда скалярное произведение 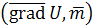 равно равно 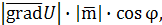 но но
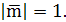 Значит: Значит:
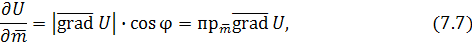
т.е. производная скалярной функции U = f(x; y; z)
в точке M
в направлении вектора 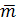 равна проекции равна проекции 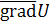 на направление вектора на направление вектора 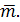
Из формулы () следует, что, когда направление вектора 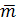 совпадает с направлением вектора совпадает с направлением вектора 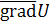 , производная по направлению , производная по направлению 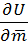 имеет своё наибольшее значение, т. е. вектор имеет своё наибольшее значение, т. е. вектор 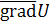 , вычисленный в точке М
, показывает направление наибольшего возрастания скалярного поля, и скорость его возрастания равна , вычисленный в точке М
, показывает направление наибольшего возрастания скалярного поля, и скорость его возрастания равна 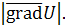
 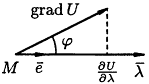 В направлении, перпендикулярном направлению В направлении, перпендикулярном направлению 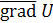 , как это следует из формулы (), , как это следует из формулы (), 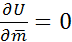 , т. е. в этом направлении из точки М
поле не меняется. , т. е. в этом направлении из точки М
поле не меняется.
Вспомним, что, если поверхность задана уравнением F(x, y, z) = 0,
нормаль к поверхности в точке M0
(x0
,y0
,z0
)
может быть задана уравнением:
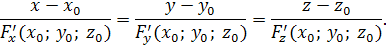
Теперь для скалярной функции U = f(x, y, z)
построим поверхности уровня f(x, y, z) = C
, тогда уравнение нормали к поверхности уровня в точке M0
(x0
, y0
, z0
)
запишется:
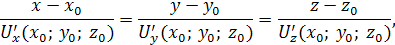
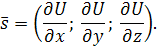
т.е. имеет направляющий вектор
Следовательно, вектор 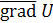 есть вектор, перпендикулярный поверхности уровня функции U = f(x, y, z)
. есть вектор, перпендикулярный поверхности уровня функции U = f(x, y, z)
.
Свойства градиента функции:
1˚ Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
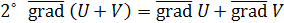
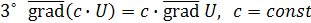
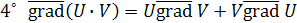
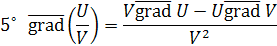
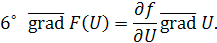
§3. ВЕКТОРНОЕ ПОЛЕ И ЕГО ЦИРКУЛЯЦИЯ
Одной из характеристик стационарного векторного поля служат векторные линии.
Векторной
называется линия, в каждой точке которой направление касательной совпадает с направлением векторного поля в данной точке.
Пусть задано векторное поле
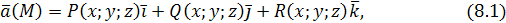
тогда вектор
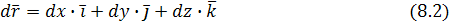
коллинеарен вектору поля 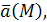 т. е. т. е.
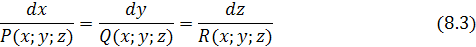
Следовательно, уравнение векторных линий поля можно получить, решив систему дифференциальных уравнений:
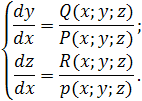
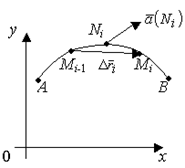 Найдем работу, которая совершается при перемещении материальной точки М
из точки А
в точку В
вдоль некоторого гладкого контура L
под действием непрерывного силового поля Найдем работу, которая совершается при перемещении материальной точки М
из точки А
в точку В
вдоль некоторого гладкого контура L
под действием непрерывного силового поля 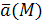 (рис. 10). (рис. 10).
Контур L
разбиваем на n
элементарных дуг точками
А = М0
, М1
, ..., Мi-1
, Мi
, ..., Мn
= В
.
Если элементарные дуги достаточно малы, то в силу непрерывности 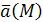 можно считать, что на каждой элементарной дуге сила можно считать, что на каждой элементарной дуге сила 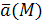 является постоянной и равна своему значению является постоянной и равна своему значению 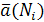 в некоторой точкеNi
, в некоторой точкеNi
,
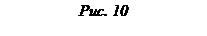 При этих предположениях элементарная работа ΔAi
, совершаемая при передвижении материальной точки вдоль дуги Мi - 1
Мi
, приближённо равна скалярному произведению При этих предположениях элементарная работа ΔAi
, совершаемая при передвижении материальной точки вдоль дуги Мi - 1
Мi
, приближённо равна скалярному произведению
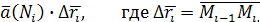
Следовательно, вся работа вдоль контура L
приближённо выражается суммой
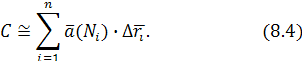
Обозначим через λ
длину наибольшей из хорд 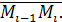 Тогда Тогда
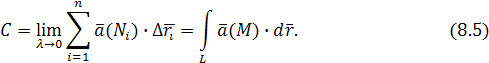
Т. е. мы пришли к криволинейному интегралу второго рода, который в координатной форме имеет вид:
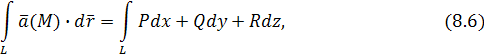
и который называют линейным интегралом
вектора 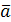 (
x
;
y
;
z
)
вдоль линии L
. (
x
;
y
;
z
)
вдоль линии L
.
Криволинейный интеграл по замкнутому контуру L
называют циркуляцией векторного поля
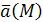 по контуру L
и обозначают: по контуру L
и обозначают:

Рассмотрим различные формы записи циркуляции. Т.к.
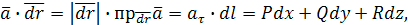
где 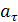 - проекция вектора - проекция вектора 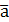 на касательную τ
, проведенную в направлении обхода кривой L
, то равенство можно записать в виде: на касательную τ
, проведенную в направлении обхода кривой L
, то равенство можно записать в виде:

или
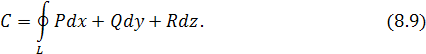
Это выражение имеет простой физический смысл: если кривая L
расположена в силовом поле, то циркуляция – это работа силы 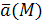 поля при перемещении материальной точки вдоль L
. поля при перемещении материальной точки вдоль L
.
Вдоль замкнутых векторных линий циркуляция отлична от нуля, т.к. в каждой точке векторной линии скалярное произведение 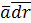 сохраняет знак: «+» - если направление вектора сохраняет знак: «+» - если направление вектора 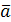 совпадает с направлением обхода векторной линии; «–» - в противном случае. совпадает с направлением обхода векторной линии; «–» - в противном случае.
Поток векторного поля
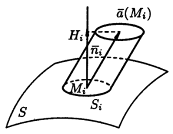 Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность. Понятие потока векторного поля удобно рассматривать на примере потока жидкости, движущейся через некоторую поверхность. Объем жидкости, протекающей в единицу времени через поверхность, расположенную в движущейся жидкости, назовем потоком жидкости через эту поверхность.
 Пусть поверхность S
расположена в поле Пусть поверхность S
расположена в поле 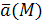 скоростей частиц несжимаемой жидкости с плотностью ρ
= 1
. Можно показать, что поток векторного поля в этом случае равен скоростей частиц несжимаемой жидкости с плотностью ρ
= 1
. Можно показать, что поток векторного поля в этом случае равен
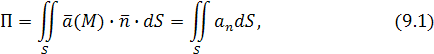
где 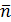 – единичный нормальный вектор к поверхности S
, расположенный по одну сторону с вектором – единичный нормальный вектор к поверхности S
, расположенный по одну сторону с вектором 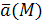 , а величина , а величина 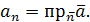
Независимо от физического смысла вектора 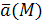 интеграл () по поверхности называют потоком векторного поля
через поверхность S
. интеграл () по поверхности называют потоком векторного поля
через поверхность S
.
Пусть 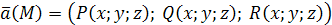 и и 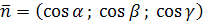 , тогда поток П вектора , тогда поток П вектора 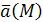 через поверхность S
можно записать в виде: через поверхность S
можно записать в виде:
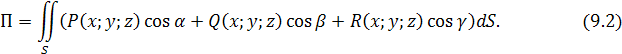
Или учитывая связь поверхностных интегралов первого и второго родов, можно записать поток П через поверхностный интеграл в координатах:
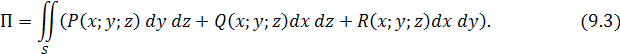
Дивергенция векторного поля. Формула Остроградского–Гаусса в векторной форме
Пусть задано векторное поле
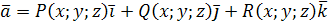
Дивергенцией или расходимостью
векторного поля 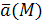 называется скалярная функция, определяемая равенством: называется скалярная функция, определяемая равенством:
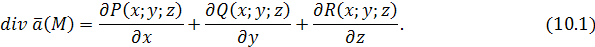
На этот раз векторное поле 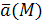 порождает скалярное поле порождает скалярное поле 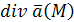 . .
С учетом понятий дивергенции и потока векторного поля формулу Остроградского–Гаусса можно представить в форме:
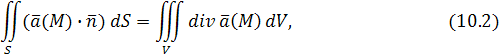
т. е. поток векторного поля 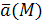 через замкнутую поверхность S
в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью. через замкнутую поверхность S
в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.
На основании формулы () можно записать:
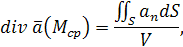
и, переходя к пределу, стягивая V
в точку М
(при этом величина V
→ 0
), имеем:
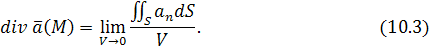
То есть 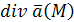 есть предел отношения потока поля есть предел отношения потока поля 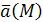 через бесконечно малую замкнутую поверхность, окружающую точку М
, к величине объёма, ограниченного этой поверхностью. Из этого следует, что дивергенция не зависит от выбора системы координат. через бесконечно малую замкнутую поверхность, окружающую точку М
, к величине объёма, ограниченного этой поверхностью. Из этого следует, что дивергенция не зависит от выбора системы координат.
Если поток
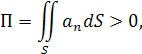
то в область V
втекает большее количество жидкости, чем вытекает из неё, т.е. внутри области V
имеются источники жидкости.
Если П<0
, то внутри области V
есть стоки. Но поток векторного поля характеризует интенсивность источников и стоков лишь суммарно, т.е. при П ≥ 0
внутри области V
могут быть как источники, так и стоки.
Для характеристики точки можно использовать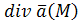 . .
Если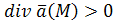 , то данная точка есть источник, если , то данная точка есть источник, если 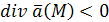 – то сток. – то сток.
Заметим, что 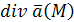 можно записать с помощью символического вектора Гамильтона можно записать с помощью символического вектора Гамильтона
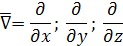
в следующем виде:
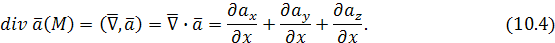
Свойства дивергенции
:
1˚ Если 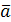 – постоянный вектор, то – постоянный вектор, то 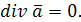
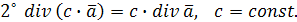
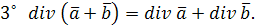
4˚ 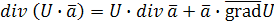 , U
– скалярная функция. , U
– скалярная функция.
Вихревой вектор поля. Формула Стокса в векторной форме
Вихревым вектором (вихрем), или ротором векторного поля
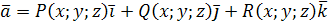
называется вектор, имеющий координаты:
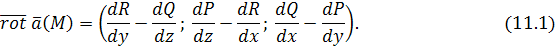
Тем самым векторное поле 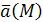 порождает векторное поле вихря порождает векторное поле вихря 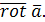
Через символический вектор Гамильтона
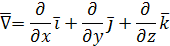
вихревой вектор записывается как векторное произведение вектора 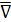 на вектор поля на вектор поля 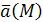 , т. е. , т. е.
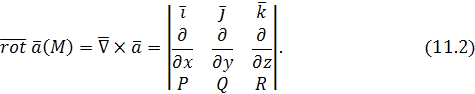
Как легко видеть, выражение
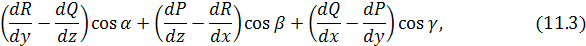
стоящее под знаком поверхностного интеграла в формуле Стокса, представляет собой скалярное произведение 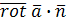 вихря векторного поля вихря векторного поля 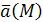 на единичный вектор нормали на единичный вектор нормали 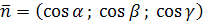 к поверхности S. к поверхности S.
Следовательно, формулу Стокса
можно представить в векторной форме следующим образом:
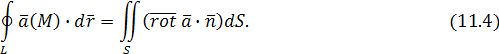
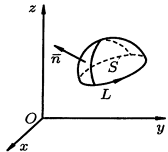 Левая и правая части формулы () представляют, соответственно, циркуляцию векторного поля Левая и правая части формулы () представляют, соответственно, циркуляцию векторного поля 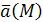 и поток его вихря. Значит, формула Стокса утверждает: циркуляция векторного поля и поток его вихря. Значит, формула Стокса утверждает: циркуляция векторного поля 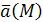 по замкнутому контуру L
равна потоку его вихря по замкнутому контуру L
равна потоку его вихря 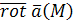 через поверхность S
, натянутую на этот контур. через поверхность S
, натянутую на этот контур.
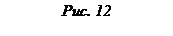 Можно определить проекцию вектора Можно определить проекцию вектора 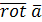 на любое направление на любое направление 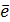 следующим образом: следующим образом:

т.е.  есть вектор, проекция которого на любое направление есть вектор, проекция которого на любое направление 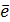 равна пределу отношения циркуляции векторного поля по контуру L
плоской площадки τ
, перпендикулярной этому направлению равна пределу отношения циркуляции векторного поля по контуру L
плоской площадки τ
, перпендикулярной этому направлению 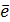 , к площади этой площадки, когда размеры этой площадки стремятся к нулю. , к площади этой площадки, когда размеры этой площадки стремятся к нулю.
Или другими словами: 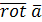 есть вектор, нормальный к поверхности, на которой плотность циркуляции достигает наибольшего значения. есть вектор, нормальный к поверхности, на которой плотность циркуляции достигает наибольшего значения.
Это, кроме прочего, означает и то, что вихрь поля (как и градиент, так и дивергенция) не зависит от выбора системы координат, а является характеристикой самого поля.
Отметим некоторые свойства ротора:
1˚ Если 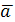 – постоянный вектор, то – постоянный вектор, то 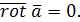
2˚ 
3˚ 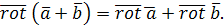
4˚ Если U
– скалярная функция, а 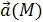 – векторная, то – векторная, то
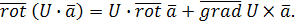
§4. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ
Векторное поле 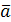 называется соленоидальным
, если во всех точках его дивергенция равна нулю, т.е. называется соленоидальным
, если во всех точках его дивергенция равна нулю, т.е. 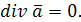 Примерами соленоидальных полей являются: поле скоростей вращающегося твердого тела; магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и т.д. Примерами соленоидальных полей являются: поле скоростей вращающегося твердого тела; магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и т.д.
Векторное поле называется безвихревым
, если его ротор тождественно равен нулю в области определения поля: 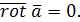
Векторное поле 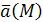 называется потенциальным
, если оно является полем градиентов некоторой скалярной функции φ(M)
, т. е. называется потенциальным
, если оно является полем градиентов некоторой скалярной функции φ(M)
, т. е.  В этом случае функция φ(M)
называется потенциалом
поля. В этом случае функция φ(M)
называется потенциалом
поля.
Имеет место важное утверждение.
Теорема
Если векторное поле 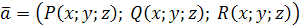 непрерывно дифференцируемо в замкнутой односвязной области V
, то каждое из следующих четырёх предложений равносильно любому другому из них: непрерывно дифференцируемо в замкнутой односвязной области V
, то каждое из следующих четырёх предложений равносильно любому другому из них:
- 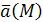 – потенциальное поле; – потенциальное поле;
- 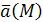 – безвихревое поле; – безвихревое поле;
- циркуляция поля по любому замкнутому контуру, лежащему внутри области V
, равна нулю;
- криволинейный интеграл
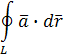
не зависит от формы пути интегрирования.
Если φ(М)
– потенциал поля , то потенциалом этого поля, как легко видеть, будет и любая другая функция вида ψ(М) = φ(М) + const
.
Любой потенциал φ(М)
поля 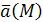 очевидно, можно представить в виде: очевидно, можно представить в виде:
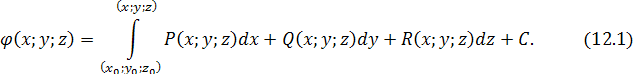
Отметим важное свойство указанных выше специальных векторных полей.
Теорема
Произвольное векторное поле 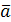 всегда может быть представлено в виде суммы потенциального поля всегда может быть представлено в виде суммы потенциального поля 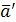 и соленоидального поля и соленоидального поля 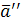 , т.е. , т.е. 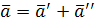 . .
Заметим, что для соленоидального поля можно определить векторный потенциал поля.
§5. ОПЕРАТОР ЛАПЛАСА. ГАРМОНИЧСЕКИЕ ФУНКЦИИ
Рассмотрим дифференциальную операцию второго порядка 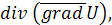 где U
– скалярная функция. Тогда где U
– скалярная функция. Тогда
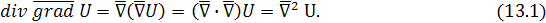
И так как
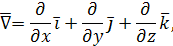
то скалярный квадрат записывают в виде:

и, следовательно
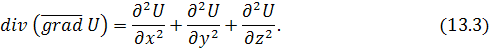
Подобно символическому оператору Гамильтона 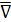 , можно ввести символический оператор: , можно ввести символический оператор:
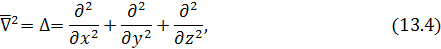
называемый оператором Лапласа
.
Скалярная функция φ(x; y; z)
называется гармонической
в некоторой области, если она непрерывна в этой области вместе со своими производными 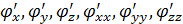 удовлетворяет уравнению удовлетворяет уравнению
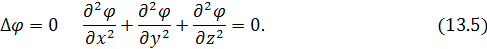
ЗАКЛЮЧЕНИЕ
Векторный анализ — раздел математики, изучающий вещественный анализвекторов в двух или более измерениях. Методы векторного анализа находят большее применение в физике и инженерии.
Векторный анализ изучает векторные поля — функции из n
-мерного векторного пространства в m
-мерное — и скалярные поля — функции из n
-мерного векторного пространства во множество скаляров.
Многие из результатов векторного анализа рассматриваются как частные случаи результатов из дифференциальной геометрии.
Для получения основных соотношений, используемых в векторном анализе, оказывается практически важным рассмотрение криволинейных и поверхностных интегралов, и их геометрических приложений. Так, например, теорема Стокса в векторной форме приобретает совершенно новый физический смысл.
Практически полезным является и введение оператора Гамильтона, с его помощью удобно записывать векторные операции первого порядка (градиент, дивергенция, ротор), а также комбинации со скалярными и векторными функциями. Для введения дифференциальных операций второго порядка используется оператор Лапласа. Дифференциальное уравнение Лапласа 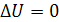 играет важную роль в различных разделах математической физики. играет важную роль в различных разделах математической физики.
К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Математическим ядром теории поля являются рассмотренные нами понятия градиента, потока, потенциала, дивергенции, ротора, циркуляции и др. Эти понятия важны и в усвоении основных идей математического анализа функций многих переменных.
СПИСОК ЛИТЕРАТУРЫ:
1. Березанский Ю. М., Левитан Б. М.. Функциональный анализ/ http://www.cultinfo.ru/fulltext/1/001/008/117/905.htm
2. Бронштейн И.Н., Семендяев К.А. Справочник по математике для и инженеров и учащихся втузов. – М.: Наука, 1964. – 608 с.
3. Выгодский М.Я. Справочник по высшей математике. – М.: Наука, 1966. – 872 с.
4. Квальвассер В.И., Фридман М.И. Теория поля. Теория функций комплексного переменного. Операционное исчисление. – М.: Высшая школа, 1967. – 240 с.
5. Кузнецов Д.С. Специальные функции. – М.: Высшая школа, 1965. – 424 с.
6. Лекции по математическому анализу: Учеб. для вузов/ Г.И. Архипов, В.А. Садовничий, В.Н. Чубариков; Под ред. В.А. Садовничего. – 4-е изд., испр. – М.: Дрофа, 2004. – 640 с.
7. Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. Справочное пособие поп высшей математике. Т.3. Ч.2: Математический анализ: кратные и криволинейные интегралы. Изд. 6-е. – М.: КомКнига, 2007.
8. Магазинников Л.И. Функции комплексного переменного. Ряды. Интегральные преобразования. Учебное пособие. – Томск: Томский межвузовский центр дистанционного образования, 1999. – 205 с.
9. Панов В.Ф. Математика древняя и юная. – 2-е изд. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2006.
10. Письменный Д.Т. – Ч.2 – 4-е изд. – М.: Айрис-пресс, 2006.
11. Фихтенгольц Г.М. Основы математического анализа. Т. 2. – М.: Государственное издательство технико-теоретической литературы, 1956. – 464 с.
12. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. – М.: Наука, 1969. – 800 с.
13. www.wikipedia.ru
|