ФГОУ ВПО «Финансовая академия при Правительстве Российской Федерации»
Кафедра «Макроэкономика»
Курсовая работа
на тему
«Экономические риски: причины их возникновения и способы снижения
»
Выполнил
:
студент группы РЦБ 2-2
Синицын Борис Владимирович
Научный руководитель
:
доктор экономических наук, профессор
Альпидовская Марина Леонидовна.
Москва
2009.
Содержание:
Введение_ 3
Глава 1. Выбор в условиях риска и неопределенности.3
§1. Понятие неопределенности и риска.3
§2. Классификация рисков.3
§3. Измерение и оценка риска.3
§4. Теория ожидаемой полезности. Функции полезности и вероятности.3
§5. Отношение к риску.3
§6. Способы снижения риска и неопределенности.3
Глава 2. Рисковые активы.3
§1. Модель «средняя – стандартное отклонение» для рисковых активов.3
§2. Равновесие на рынке рисковых активов.3
§3. Выравнивание доходности активов и линии фондового рынка.3
Заключение_ 3
Список литературы_ 3
Приложения_ 3
I.
Наука о риске сегодня необходима, ибо риск и неопределенность - это детище тех проблем, которые везде, которые нужны каждому, с другой стороны, общество не может жить без них и двигаться вперед. Все возможные колебания, нестабильность будущего… Необходимы общеконцептуальные представления, нужна систематизация знаний. Хаотичные, случайные процессы, происходящие в экономике, убедили людей в этом. Данная работа посвящена попытке систематизировать имеющиеся научные знания о таких явлениях, как риск и неопределенность.
В начале стоит отметить, что сама по себе проблема довольно молода – основная доля исследования приходится на 20 век. Связано это, конечно, с тем, что именно 20 век и показал необходимость тщательного изучения рисков и неопределенности. Век, когда бурно развивалось предпринимательство, становится колыбелью для случайных процессов. Каков будет спрос на выпускаемую продукцию, например, в следующем году? Насколько возрастет или наоборот упадет стоимость закупаемых на стороне материалов? Можно составить прогноз, провести анализ ситуации. Но практически никогда невозможно точно знать наперед, что и как произойдёт. Неопределенность похожа на ящик Пандоры – можно получить всё, что угодно, как хорошего, так и плохого. Имеются в виду все возможные прибыли, связанных с деятельностью в условиях неопределенности. Но не стоит забывать и об издержках и убытках. Хаотичность и непредсказуемость процессов, культивируемых неопределенностью порой заставляет восторгаться, а порой и бояться.
Сегодня основные задачи направлены на прикладную сторону этого вопроса – управление риском или снижение. Стоит сказать, что в этой сфере не наблюдается какого-то единого, применимого ко всем четкого подхода, ибо разнообразие рисков заставляют изучать их применительно к сфере деятельности, в которой они возникают. В области финансовой деятельности изучением проблем рисков занимаются в том числе и частные компании. Например, JPMorgan, которая разработала свою методику оценки рисковых активов. Помимо этого с рисками очень тесно связана страховая сфера деятельности. Риски, связанные с управлением – одна из главных проблем в менеджменте.
Однако из-за разброса по прикладному назначению на настоящее время так и не существует единой теории риска и неопределенности. Конечно, это не должно отталкивать людей и уменьшать их интерес. Скорее наоборот. Созданная брешь обречена быть заделанной. Вопрос лишь в том – когда.
Данная работа представляет собой анализ монографических публикаций и статей и других трудов известных экономистов ХХ века по тематике риска и неопределенности. Импульсом к выбору именно этой темы послужили актуальность и одновременная малоизученность этих феноменов в экономической деятельности. Поэтому цель работы – углубление знаний по проблеме риска и неопределенности в экономике, а так же по возможности переосмысление имеющейся информации в новых условиях.
Перед тем, как приступить к содержанию работы, хотелось бы наметить цели: 1) попытка систематизировать существующие представления теории риска и неопределенности, в частности, о поведении человека и его выборе в этих условиях, 2) раскрыть основные подходы проблеме рисковых активов в условиях неопределенности.
Что же такое риск? И в каких областях человеческой деятельности мы с ним встречаемся?
Термин риск произошел от греческого «risikon» – утёс. На уровне обыденного познания риск понимается как некая опасность неблагоприятного исхода и носит скорее негативную, чем позитивную, окраску. В словаре Ожегова риск определяется как «опасность, возможность опасности» или «действие наудачу в надежде на счастливый исход». В современном экономическом словаре риск – это опасность возникновения непредвиденных потерь ожидаемой прибыли, дохода или имущества, денежных средств, других ресурсов в связи со случайным изменением условий экономической деятельности, неблагоприятными обстоятельствами. Тщательный анализ источников показывает, что в настоящее время не существует четко определенного понятий риска и неопределенности. Тем не менее, понятно, что они играют серьезную роль в экономической деятельности. Поэтому для наиболее точного представления об этих понятиях стоит изучить развитие теорий с самого начала до наших дней.
Начальные попытки оценки рисковых решений в условиях неопределенности восходят к работам математика Д. Бернулли, который предположил, что математическое ожидание успеха должно определяться с учетом его субъективной оценки. Исследую т. н. Санкт-Петербургский парадокс[1]
, он утверждал, что, принимая свои решения в условиях неопределенности, индивид руководствуется не априорно подсчитанным математическим ожиданием шансов на успех, а “моральным ожиданием успеха, при котором вероятность взвешивается на полезность дохода”. При этом предельная полезность дохода снижается с ростом общей. При уменьшающейся предельной полезности люди будут настаивать на увеличении выигрыша, чтобы компенсировать риск. “Никто не станет платить 1 доллар за шанс выиграть 2 доллара с вероятностью 50 процентов”, — утверждал он. Впоследствии эта гипотеза, а вернее предположение, что ожидание успеха – результат субъективных оценок, получило отражение в известной теории “функции полезности Неймана—Монгерштерна”, а также в работе Нобелевского лауреата по экономике французского ученого М. Алле “Поведение рационального человека в условиях риска”.
Во второй половине XIX столетия гипотеза Д. Бернулли инициировала возникновение самостоятельного психофизического направления школы исследования предпринимательского риска (т.е. поведения индивидуумов в условиях неопределенности), основателями которой являлись В. Вебер и Г. Фехнер. Сформулированный ими “Закон Вебера—Фехнера” утверждал, что осязаемые различия в восприятии явлений прямо пропорциональны интенсивности стимулов. При этом под стимулами ими понимался прирост доходов. Иными словами, этот теоретический вывод утверждал, что выбор решений в условиях неопределенности в значительной степени зависит от субъективных оценок уровня риска и доходности конкретными людьми.
В рамках школы маржиналистов дальнейшее развитие теории риска связано с исследованиями Й. фон Тюнена. В своей работе “Изолированное государство” (1850 г.) он впервые рассмотрел сущность инновационных рисков в процессе предпринимательской деятельности. Характеризуя инновационную деятельность как одну из наиболее рискованных в экономике, он утверждал, что вознаграждение предпринимателя является доходом за принятие на себя тех рисков, которые из-за непредсказуемости не примет на себя и не покроет ни одна страховая компания. Это впервые наметило различия между “условиями риска” (т.е. условиями, вероятность которых может быть рассчитана) и “условиями неопределенности” (т.е. условиями, вероятность которых непредсказуема и не поддастся количественному анализу).
Определенный вклад в развитие инновационной теории риска был внесен представителем школы институционализма Й. Шумпетером. В своей книге “Теории экономического развития” (1912 г.) он предложил новый подход к оценке роли предпринимателей, осуществляющих инновационную деятельность в условиях риска. Он утверждал, предприниматель, осуществляющий инновационную деятельность в условиях высокого риска, является источником всех положительных динамических изменений в экономике. Однако магистральное направление экономической теории того времени проигнорировало этот вывод Шумпетера, поскольку он не укладывался в рамки статического равновесного анализа и противоречил выводам о предпринимательском доходе как результате неисчислимого (а соответственно и нестрахуемого) риска.
Наряду с Й. Шумпетером одним из первых ученых, осветивших проблему риска и неопределенности, был Ф. Найт. Он дал четкие рамки определениям риска и неопределенности, и, следовательно, провёл различия между ними. Однако, как и во многих остальных работах по этой теме, четкого определения риска и неопределенности не даётся. Он писал: «Когда речь идёт о риске, распределение исходов … известно либо благодаря априорным расчетам, либо из статистических данных прошлого опыта, тогда как в условиях неопределенности это не так по той общей причине, что ситуация, с которой приходится иметь дело, весьма уникальна, и нет возможности сформировать какую-либо группу случаев».[2]
Риск возникает только тогда, когда имеется какое-то ограниченное количество вероятных исходов, неопределенность же не имеет заранее определенного количества исходов. Соответственно риск имеет такую природу, которой можно так или иначе управлять или влиять на нее через известную вероятность. Если известно распределение различных возможных результатов в группе, становится возможным путем надлежащей группировки или объединения случаев устранить всякую неопределенность. Ее можноустранить, но это не значит, что так и будет сделано. Поэтому, как тавтологично бы ни звучало, в ситуации принятия единичного решения не существует никакой разницы между измеримым риском и неизмеримой неопределенность. И всё же изначально неопределенность имеет кардинально противоположную сущность, не имеющую вероятность, а следовательно, не поддающуюся управлению и воздействию. Эта неопределенность, с которой сталкивается большинство предпринимателей, “не может быть ни застрахована, ни капитализирована, ни оплачена в форме заработной платы”. Предприниматель не знает заранее цену, по которой будет продан его продукт, но в то же время обязан заранее расплатиться с собственниками факторов производства.
Вследствие того, что в некоторых моментах ситуация риска, то есть та, в которой известно конечное число исходов и вероятностей, не отличается от неопределенности, то Найт под словом риск имеет в виду так называемую измеримую неопределенность, а под неопределенностью – неизмеримую. Чтобы сохранить различие между измеримой и неизмеримой неопределенностью, о котором шла речь выше, мы можем использовать термин "риск" для обозначения первого типа неопределенности и собственно термин "неопределенность" – для второго.[3]
Помимо этого Ф. Найт рассуждает на тему причин появления риска и неопределенности. Рассматривая отдельно механизмы функционирования экономики в моделях совершенной и несовершенной конкуренции, он утверждает, что риск и неопределенность возникают во время перехода от первой ко второй. В то время как необходимым условием совершенной конкуренции является полнота информации, в несовершенной конкуренции информация в руках субъекта либо ограничена, либо не поддается полному анализу из-за больших объемов. Так или иначе, при решениях приходится прибегать к оценкам, которые в свою очередь могут привести к ожидаемому результату, а могут и не.
Теоретические выводы Ф. Найта позволили впервые со времен А. Смита четко отделить понятия риска от неопределенности, но так и не дали их точной трактовки.
Теория риска получила определенное развитие и в работах представителей экономической школы кейнсианства. В своей статье “Общая теория занятости” Дж. Кейнс акцентирует внимание на неопределенности, господствующей в экономической жизни и не поддающейся вероятностным оценкам.
Эта неопределенность в значительной степени влияет на экономическое поведение людей. Вследствие этой неопределенности, отмечал он, инвестиции обречены колебаться вместе с колебаниями доверия в сфере бизнеса, которые не находятся ни в какой предсказуемой зависимости от стандартных экономических величин.
Современный синтез теории риска включает в себя многочисленные его характеристики, выявленные ранее, и имеет скорее практическую направленность — в страховом бизнесе, банковском деле, инвестициях, предпринимательстве и т.д.
Анализ многочисленных толкований риска позволяет выявить характерные для рисковой ситуации моменты:
· случайный характер события, который определяет, какой из возможных исходов реализуется на практике (наличие неопределенности);
· наличие альтернативных решений;
· известны (или можно определить) вероятности исходов и ожидаемые результаты;
· вероятность возникновения убытков;
· вероятность получения дополнительной прибыли.
Говоря о теории риска и неопределенности в российской экономической науке, стоит заметить, что этой проблеме не уделено дόлжного внимания. Ориентация в течение длительного времени на преимущественно экстенсивное развитие народного хозяйства страны, чрезмерно высокая степень централизации управления, господство административных методов управления и не подразумевали учета неопределенности и риска. Кроме того, при «экономике дефицита» не было заинтересованности и желания идти на риск, менять сложившуюся технологию производства. Но с переходом на рыночную экономику, либерализацию цен и другие экономические свободы, проблема риска и неопределенности, само собой, стала весьма актуальной.
Тем не менее, есть такое определение риска: «деятельность, связанная с преодолением неопределенности в ситуации неизбежного выбора, в процессе которой имеется возможность количественно и качественно оценить вероятность достижения предполагаемого результата, неудачи либо отклонения от цели».[4]
Данное определение, во-первых, содержит разделение понятий неопределенности и риска (данные Ф. Найтом), во-вторых, охватывает все возможные исходы, как положительные, так и отрицательные, в-третьих, рисует тесную связь риска и неопределенности.
Таким образом, ситуация риска (рисковая ситуация) — это разновидность неопределенности, когда наступление событий вероятно и может быть определено, т.е. в этом случае объективно существует возможность оценить вероятность событий, возникающих в результате осуществления экономической деятельности.
Многообразие рисковых ситуаций на практике заставляет сравнивать их между собой по различным характеристикам. Поскольку главной задачей является оценка степени рисков, то их систематизация по одинаковым признакам, распределение по группам существенно облегчит этот процесс.
Один из вариантов классификации рисков хозяйственной деятельности представлен в Приложении А.
По характеру последствийриски подразделяются на чистые и предполагаемые. Особенность чистых рисков (их иногда называют статистическими или простыми) заключается в том, что они практически всегда несут в себе отрицательный результат деятельности; их причинами могут быть стихийные бедствия, несчастные случаи, недееспособность руководителей фирм и т.д. Так как потери такого рода всегда можно подсчитать, то именно такие риски чаще других покрываются страхованием.
Предполагаемые риски, которые называют также динамическими или спекулятивными, несут в себе либо потери, либо дополнительную прибыль. Эти риски характерны в бόльшей степени для предпринимательской деятельности; их причинами могут быть изменение курсов валют, конъюнктуры рынка, условий инвестиций и др.
По сфере возникновения, различают следующие виды рисков:
• производственный риск, связанный с невыполнением предприятиями своих планов и обязательств по производству продукции, товаров, услуг, других видов производственной деятельности в результате воздействия как внешней среды, так и внутренних факторов;
• коммерческий риск — это риск потерь в процессе финансово-хозяйственной деятельности; его причинами могут быть снижение объемов реализации, непредвиденное снижение объемов закупок, повышение закупочной цены товара, повышение издержек обращения, потери товара в процессе обращения и др.;
• финансовый риск возникает в связи с невозможностью выполнения фирмой своих финансовых обязательств; причинами являются изменение покупательной способности денег, неосуществление платежей, изменение валютных курсов и прочее.
В зависимости от основной причины возникновениярисков они делятся на следующие категории:
• природно-естественные риски – это риски, связанные с проявлением стихийных сил природы;
• экологические риски связаны с наступлением гражданской ответственности за нанесение ущерба окружающей среде;
• политические риски – это возможность возникновения убытков или сокращения размеров прибыли, являющихся следствием государственной политики;
• транспортные риски связаны с перевозками грузов различными видами транспорта;
• имущественные риски — это риски от потери имущества предпринимателя по не зависящим от него причинам;
• торговые риски зависят от убытков в случае задержки платежей, непоставки товара, отказа от платежа и т.п.
Большая группа рисков связана с покупательной способностью денег. Сюда относятся:
• инфляционные риски, которые обусловлены обесцениванием реальной покупательной способности денег, при этом предприниматель несет реальные потери;
• дефляционный риск связан с тем, что при росте дефляции падает уровень цен и, следовательно, снижаются доходы;
• валютные риски связаны с изменением валютных курсов, они относятся к предполагаемым рискам, поэтому при потерях одной из сторон в результате изменения валютных курсов другая сторона, как правило, получает дополнительную прибыль, и наоборот;
• риск ликвидности связан с потерями при реализации ценных бумаг или других товаров из-за изменения оценки их качества и потребительской стоимости.
Инвестиционные рискисвязаны с возможностью недополучения или потери прибыли в ходе реализации инвестиционных проектов, они включают в себя следующие подвиды:
• риск упущенной выгоды заключается в том, что возникает финансовый ущерб в результате неосуществления некоторого мероприятия;
• риск снижения доходности связан с уменьшением размера процентов и дивидендов по портфельным инвестициям; он делится на процентный риск, возникающий в результате превышения процентных ставок, выплачиваемых по привлеченным средствам, над ставками по предоставленным кредитам, и кредитный риск, возникающий в случае неуплаты заемщиком основного долга и процентов, причитающихся кредитору;
• биржевые риски представляют собой опасность потерь от биржевых сделок;
• селективные риски возникают из-за неправильного формирования видов вложения капиталов, вида ценных бумаг для инвестирования;
• риск банкротства связан с полной потерей предпринимателем собственного капитала из-за его неправильного вложения.
Естественно, анализ классификационных признаков, видов и подвидов риска можно продолжить, но это приведет к перечислению мнений различных исследователей и специалистов, что не даст ответа на основной вопрос – какой подход, какая классификация является основной, в какой степени она будет способствовать снижению степени риска.
После того, как выяснены основные подходы к определению понятий и классификациям, мы приближаемся к следующей проблеме – потребности измерить или каким-то образом оценить риск. Имея оценку рисков, мы можем сравнивать их между собой, принимать, отвергать и т. д. В общем, оценка и измерения необходимы для принятия решения в рисковой ситуации. Как отмечалось выше, риск включает в себя оцененную любым способом вероятность некоторых исходов. Именно вероятность является количественной составляющей риска. В теории риска можно встретить три общих типа вероятностей:
Априорная или математическая. Это вероятность, полученная на основе научного закона или определенного логического принципа, «абсолютно однородная классификация случаев, во всем идентичных[5]
». Сюда входят все события, вероятность наступления исходов которых мы можем сосчитать, например, используя классическое определение вероятности из курса теории вероятности.
Статистическая. Это вероятность, полученная нами благодаря статистическому наблюдению за данным событием в прошлом. Стало быть, для расчета обязательно иметь накапливающуюся определенный период времени информацию и обязательно об идентичном событии. На практике камнем преткновения является то, что зачастую невозможно ограничить наблюдение только за абсолютно идентичными событиями. К примеру, если ведется наблюдение за студентами, забывающими студенческий билет, из 100 студентов забывают 15 человек. В среднем вероятность того, что один студент забудет билет = 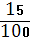 . Но понятно, что это вероятность будет разной у того, кто забывает билет хронически, и у того, кто почти не забывает. Поэтому, несмотря на то, что подобную вероятность реальнее рассчитать, она менее точна, чем априорная. . Но понятно, что это вероятность будет разной у того, кто забывает билет хронически, и у того, кто почти не забывает. Поэтому, несмотря на то, что подобную вероятность реальнее рассчитать, она менее точна, чем априорная.
Ожидаемая. Для определения этого рода вероятности не требуется никаких рациональных алгоритмов. Находится такая вероятность путем субъективной оценки, решения. Не будем вдаваться в причины, просто имеет смысл отметить, что это явление происходит в результате взаимодействия человеческого сознания и реальности. Именно такой случай имеет самое широкое распространение на практике. Вместе с тем он сложнее всего поддается объяснению. И в самом деле, трудно найти менеджера, который смог бы рассказать, в чем причина его успеха. Зачастую он и сам не знает. И даже если знает, не сможет научить другого, не сможет выразить словами то, что понимает. Таким образом, это самая «гадательная» из всех вероятностей. Тем не менее, она зачастую действительно помогает повысить надежность принимаемых решений.
Теория измерения риска бывает порой весьма далека от практики. В реальной среде, например, в бизнесе или менеджменте, очень редко можно применить априорную вероятность полностью. Ведь обязательным критерием ее применения является однородность групп вероятностных исходов, а это, в свою очередь, понятие идеальное и недостижимое. Поэтому результаты измерения вероятности по априорному методу будут весьма далёкими от реальности. Часто неприменима и статистическая вероятность - из-за уникальности событий происходящих. В таких условиях место остается лишь ожидаемой вероятности.
Когда известны вероятности событий, составляющих полную группу возможных в рисковой ситуации, их можно подвергнуть анализу. Вот некоторые показатели этого анализа:
Среднее значение. С точки зрения математики среднее значение – средневзвешенная оценка из всех возможных результатов с учетом соответствующих вероятностей. Оно рассчитывается по формуле математического ожидания (Приложение Б). Притом, если группа событий полная, то сумма всех вероятностей будет равна единице.
Экономический смысл этого показателя, увы, ограничивается рамками теории: он показывает, какое значение примет результат при бесконечно большом количестве повторений события. На практике же данное событие (рисковая ситуация) происходит один раз – и в этот момент требуется принять решение.
Однако одного среднего значения недостаточно для анализа. Ведь, как уже замечалось выше, единичные события (то есть те, которые реально имеют вероятность настать) могут иметь разное отклонение от среднего значения. Для расчета этого отклонения существует два показателя: дисперсия и среднеквадратичное отклонение.
Дисперсия – средневзвешенная величина квадратов отклонений действительных результатов от средних значений (Приложение В).
Для большей наглядности используют корень из дисперсии, называемый средним квадратичным отклонением.
Пример применения данных показателей покажем на ситуации (все расчеты приведены в Приложении Г):
1. Фирма инвестирует 50 млн. руб. и, по мнения экспертов, через год с вероятностью 2/6 получит текущую дисконтированную стоимость (PDV), равную 250 млн. руб., с вероятностью 1/6 PDVсоставит 100 млн. руб. и с вероятностью 3/6 PDV=0.
2. При той же сумме инвестиций фирма с вероятностью 1/6 получит 600 млн. руб. и ничего не получит в остальных случаях (вероятность = 5/6).
Для первого проекта среднее значение составит 100 млн. руб., так же, как и для второго. Это означает, что оба проекта принесут фирме среднюю ожидаемую выручку, равную удвоенной величине инвестиций.
Но полученные величины – лишь гипотетические. Каково же будет отклонение реального дохода от средней величины? Чтобы найти, рассчитаем дисперсию.
Получается, что во втором проекте дисперсия в 4 раза выше. Это означает, что во втором проекте риск больше. Для того, чтобы узнать насколько, рассчитаем среднеквадратичное отклонение. Для первого случая оно составит 111, 9 млн. руб., а для второго 223,6 млн. руб. Эти величины показывают, на сколько фактический доход будет отличаться от ожидаемого. В последнем случае отличие примерно в 2 раза больше, чем в первом, что так же говорит о более высоком уровне риска.
Однако описанная выше ситуация – идеальна. На практике крайней редко случаются такие ситуации, когда можно точно найти вероятность событий и тем более все возможные события. Кроме того вышеописанные методы, исходя из теории вероятности, применимы лишь к идеальной ситуации, когда количество повторений рисковых событий стремится к бесконечности. Во всех остальных случаях, особенно когда требуется один раз принять решение для всей ситуации, равенство не соблюдается.
Поэтому возникает вопрос, в таком случае, зачем нужны, с одной стороны, идеальные математические выкладки и, с другой, чересчур «гадательные» субъективные оценок идвидуумов? В чем заключается их применение на практике? И чему придавать предпочтение? На эти вопросы нет единого мнения в настоящее время. Несмотря на то, что математические вычисления далеки от реальности, а ожидаемая (субъективная) вероятность зачастую выявляется с помощью догадок и шатких предположений, тем не менее, и те, и другие имеют практическое применение. Математические расчеты зачастую служат своеобразным ориентиром. А процесс формирования наших оценок порой весьма сложен с психофизиологической точки зрения и может рождаться благодаря бесчисленному множеству аналитических процессов, проходящих в подсознании. В любом случае, использование всех типов вероятностей, правильное сочетание и анализ помогает взвесить все альтернативы в рисковых ситуациях с наиболее возможной точностью.
Однако знание или тем более незнание вероятностей в рисковых ситуациях всё еще не решает проблему выбора в условиях неопределенности.
С этим кругом вопросов призвана справляться теория ожидаемой полезности. Модели ожидаемой полезности изучают выбор между рисковыми перспективами (т.е. произведениями векторов исходов 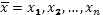 и вероятностей наступления каждого из них и вероятностей наступления каждого из них 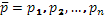 .) как с одним, так и с несколькими возможными исходами. Пусть анализируется n
таких исходов. Если обозначить векторы исходов через .) как с одним, так и с несколькими возможными исходами. Пусть анализируется n
таких исходов. Если обозначить векторы исходов через 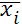 , а вероятности, связанные с каждым из них, через , а вероятности, связанные с каждым из них, через 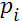 , то ожидаемая полезность в общем виде может быть определена как модель, предсказывающая или предписывающая максимизацию индивидом , то ожидаемая полезность в общем виде может быть определена как модель, предсказывающая или предписывающая максимизацию индивидом 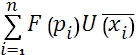 .Основными особенностями модели в этой общей форме являются: 1) независимость альтернативных исходов (т.е. каждый имеет свой собственный уровень полезности); 2) независимы и преобразования вероятностей и исходов; и 3) мультипликативное сочетание вероятностей и исходов по типу вычисления ожидаемых величин после некоторых преобразований, заданных функциями F
и U
. .Основными особенностями модели в этой общей форме являются: 1) независимость альтернативных исходов (т.е. каждый имеет свой собственный уровень полезности); 2) независимы и преобразования вероятностей и исходов; и 3) мультипликативное сочетание вероятностей и исходов по типу вычисления ожидаемых величин после некоторых преобразований, заданных функциями F
и U
.
В рамках этой общей модели ожидаемой полезности существует множество разновидностей, которые различаются между собой 1) по способу измерения полезности, 2) по допустимым типам преобразования вероятностей F
(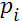 ), и 3) по способу измерения исходов ), и 3) по способу измерения исходов 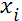 . .
Поэтому имеет смысл рассмотреть формирование моделей ожидаемой полезности с исторической точки зрения. В частности впервые об ожидаемой полезности стало известно из работ Д. Бернулли. Как уже было отмечено в начале работы, в процессе исследования т. н. Санкт-Петербургского парадокса были выдвинуты предположения о том, что индивид руководствуется оптимизацией не ожидаемого выигрыша, а ожидаемой полезности. Напомним, что суть этого парадокса заключалась в игре, в которой подбрасывалась монета до тех пор, пока не выпадет герб. Причем выигрыш будет равен  ден. единиц. Если составить закон распределения случайной величины выигрыша, то значения будут такими: 2, 4, 8, 16 и т.д… ( ден. единиц. Если составить закон распределения случайной величины выигрыша, то значения будут такими: 2, 4, 8, 16 и т.д… (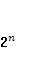 ), - а вероятности будут соответствовать ), - а вероятности будут соответствовать  и т.д… . Нетрудно подсчитать по формуле математического ожидания, что ожидаемый доход будет равняться и т.д… . Нетрудно подсчитать по формуле математического ожидания, что ожидаемый доход будет равняться 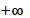 . В ответ на это Бернули вместе с известным математиком Г. Крамером предложили, что в данной ситуации для человека важен не математический подсчет ожидания, а его субъективная оценка. Зависимость между исходами и их ценностью для индивида показывает полезность и кривые безразличия. Функция полезности, предложенная Бернулли, имеет логарифмический вид (приложение Г), тем самым показывая убывание по мере роста богатства (в данном случае выигрыша). Так же он показал, что ожидаемая полезность, имеющая вид , будет конечна (ряд сходится). Однако он не ставил перед собой задачи измерения полезности, и не пытался объяснить, почему его принцип ожидаемой полезности можно считать рациональным. Вместе с тем эту теорию впоследствии неизменно отвергали как правильное объяснение, - обычно потому, что господствующее убеждение в убывающей предельной полезности заставляло считать, что существование азартных игр не может быть объяснено таким образом. . В ответ на это Бернули вместе с известным математиком Г. Крамером предложили, что в данной ситуации для человека важен не математический подсчет ожидания, а его субъективная оценка. Зависимость между исходами и их ценностью для индивида показывает полезность и кривые безразличия. Функция полезности, предложенная Бернулли, имеет логарифмический вид (приложение Г), тем самым показывая убывание по мере роста богатства (в данном случае выигрыша). Так же он показал, что ожидаемая полезность, имеющая вид , будет конечна (ряд сходится). Однако он не ставил перед собой задачи измерения полезности, и не пытался объяснить, почему его принцип ожидаемой полезности можно считать рациональным. Вместе с тем эту теорию впоследствии неизменно отвергали как правильное объяснение, - обычно потому, что господствующее убеждение в убывающей предельной полезности заставляло считать, что существование азартных игр не может быть объяснено таким образом.
Теория Бернулли как таковая является главным образом описательной моделью, хотя для своего времени сам принцип ожидаемой полезности мог выглядеть вполне убедительно.
Формальное доказательство того, что принцип максимизации ожидаемой полезности является критерием рациональности принимаемых решений, т.е. может быть выведен из нескольких аксиом, было проведено лишь в 1947 году Джоном фон Нейманом и Оскаром Моргенштерном. В нем утверждается, что "в условиях, на которых базируется анализ кривой безразличия, легко определить численную полезность[6]
", ожидаемое значение которой максимизируется в выборе среди альтернатив, предполагающих риск. И эта концепция применима к исходам любого рода, где денежные выигрыши являются лишь частным случаем (в отличие от модели Крамера и Бернулли). Именно эта общность теории, по мнению многих экономистов[7]
, и позволила ей стать основой анализа рисковых ситуаций.
Теория ожидаемой полезностиНеймана и Моргенштерна строится на следующих аксиомах:
· Аксиомы полнотыи транзитивности предпочтений. Если рисковая ситуация (далее РС) L1
предпочтительней РС L2
, то это можно записать как L1
> L2
. Полнота означает, что индивид способен всегда оценить, какая РС для него предпочтительней, а какая нежелательней. Транзитивность заключается в то, что, если L1
> L2
, L2
> L3
, то L1
> L3
.
· Аксиома непрерывности. Если существуют такие исходы x1
,x2
,x3
, что x1
>x2
>x3
, существует такая вероятность p для x1
, а для x3
–вероятность (1-p), что РС (x1
, p; x3
, (1-p)) столь же привлекательно, как РС с гарантированным исходом x2
. То есть при определенной p индивиду будет всё равно, точно получить какой-то результат или иметь риск получить результат лучше или хуже.
· Аксиома независимости. Если существуют две РС – L1
(x1
, p; x3
, 1-p) и L2
(x2
,p; x3
, 1-p), где x1
, x2
могут или связаны, или не связаны с риском – и x1
=x2
(равнозначны), то и L1
=L2
независимо от x3
.
· Если в РС L1
(x1
, p; x2
, 1-p) и L2
(x1
,q; x2
, 1-q) x1
>x2
, то L1
> L2
тогда и только тогда, когда p>q.
· Принцип сведения составных РС. При принятии решения для человека не важен порядок, в котором представлены призы и вероятности в РС, а важно лишь конечное распределение призов в РС, сочетающееся с перемножением составных вероятностей.
Пяти вышеперечисленных аксиом, достаточно, чтобы гарантировать существование такого индекса полезности, при котором ранжирование РС по их ожидаемой полезности полностью соответствует действительным предпочтениям индивида, как считают Д. Нейман и О. Моргенштерн.
Что касается самой функции полезности, то она является единственной с точностью доположительного линейного преобразования. Это означает, что если функция U(x)задает предпочтения индивида относительно исходов x, то функция U*(x) = aU(x)+ b, где a, b – числовые коэффициенты, a > 0, также задает предпочтения индивида относительно x. Оказывается, если подвергнуть функцию ожидаемой полезности положительному линейному преобразованию, то полученная в результате этого функция не только будет представлять те же самые предпочтения, но и по-прежнему будет обладать свойством ожидаемой полезности.
Это также означает, что для этой функции нет зависимости от начала координат и единицы измерения. Например, мы можем произвольно считать началом координат $10 (т.е. положить U
(10) = 0, и принять U
(10 000) равной, скажем, 100 единицам полезности (ютилям)). Используя эти две точки отсчета, индекс полезности можно легко получить с помощью простых вопросов типа "Какой достоверный доход столь же привлекателен, что и лотерея 50/50 с исходами $10 и $10000?" Если эта сумма равна $x
*, то U
(x
*) полагается равным 0,5U
(10) + 0,5U
(10 000) = 50 ютилям. До тех пор, пока такая пробная лотерея содержит исходы, полезность которых известна, мы можем определять значения полезности в других точках.
Важную роль в теории ожидаемой полезности играет понятие неприятия риска (подробнее в §5). Выпуклая вверх функция полезности, принимающая вид экспоненциальной кривой, характеризует неприятие риска, а выпуклая вниз – стремление к риску.
С точки зрения измерения полезности теория Неймана и Моргенштерна является кардиналистской, поскольку ее шкала полезности является интервальной. Однако с точки зрения предпочтений, её можно трактовать как ординалистскую, поскольку она обеспечивает лишь порядковое ранжирование лотерей. Поэтому к кардиналистской составляющей теории следует относиться аккуратно. Хотя функции полезности представляют собой интервальные шкалы, т.е. отношения разностей между уровнями полезности независимы относительно линейных преобразований, – это не означает, например, что из x
1
> x
2
> x
3
> x
4
и U(x
1
) – U(x
2
) > U(x
3
) – U(x
4
) следует, что перемещение из x
1
в x
2
должно быть более предпочтительным, чем перемещение из x
3
в x
4
. Поэтому полезность по Нейману и Моргенштерну нельзя
интерпретировать как измерение силы предпочтения в условиях определенности, что качественно отличает ее от неоклассической кардинальной полезности. Это объясняется тем, что предпочтения определяются по крайней мере двумя различными факторами, а именно: 1) силой предпочтений достоверных исходов; и 2) отношением к риску. Функция полезности Неймана и Моргенштерна является составной комбинацией этих двух факторов, которая не требует ни прямого сопоставления интервалов, ни измерения силы предпочтений. Как теория предпочтений она является всецело ординалистской. Тем не менее, она неявнопредполагает, что существует полезность неоклассического кардиналистского типа – иначе было бы психологически невозможно определить достоверный эквивалент рисковых ситуаций.
Существует, еще множество концепций ожидаемой полезности, имеющих различие в функциях полезности, но все так или иначе являются модификацией именно этой модели. Об остальных вскользь упоминается чуть ниже.
Другой аспект модели ожидаемой полезности, в котором наблюдаются различные точки зрения – это определение вероятностей. В аксиоматике теории Неймана и Моргенштерна вероятность рассматривается как элементарное понятие, численное значение которого определено объективно. Однако эмпирически понятие вероятности является куда более проблематичным как с философской, так и с практической точек зрения. Чтобы убедиться в этом, рассмотрим коротко четыре основные концепции вероятности и пределы возможностей каждой из них.
Первая – это классическая концепция Пьера Лапласа, который определил вероятность как число благоприятных элементарных исходов некоторого события, отнесенное к числу всех возможных элементарных исходов. К недостаткам этой теории можно отнести то, что это определение нелегко применить в случае бесконечного пространства исходов, и оно практически ограничивается только хорошо структурированными ситуациями. К положительным моментам, разумеется, относится формальная наглядность и относительная простота этой модели.
Якоб Бернулли, дядя Даниила Бернулли, еще раньше избежал этой тавтологии, отличив само понятие от его измерения. Он определил вероятность как "степень доверия", которая для каждого события может разниться у разных людей. Тем не менее он полагал, что искусство угадывания заключается в том, чтобы уточнять оценки неизвестных вероятностей, в частности, исследуя объективные частоты. Этот частотный подход позже был положен в основу аксиоматики Джона Венна, Ханса Рейхенбаха и Рихарда фон Мизеса которые определяли вероятность как предельное значение процента благоприятных исходов в бесконечной последовательности независимых испытаний. Такой подход является ограниченным по крайней мере с двух точек зрения. Во-первых, вероятность никогда не бывает точно измеримой численно – в лучшем случае ее можно оценить на очень большой выборке. Во-вторых, часто бывает непонятно, что следует считать пространством возможных исходов – так, если оценивается объективная вероятность попасть в авиакатастрофу, то следует ли брать все предыдущие полеты, или же только на этом маршруте, на этом типе самолета, в это время года и т.д.
Третью попытку определить вероятность объективно предприняла так называемая логическая школа Джона Мейнарда Кейнса и Гарольда Джеффриса. Эти авторы утверждали, что каждое множество эмпирических данных находится в логическом, объективном отношении к истинности некоторой гипотезы (например, о виновности кого-либо), даже если эти данные сами по себе не позволяют прийти к определенным выводам. Вероятность измеряет силу этой связи с точки зрения рационального индивида. Поскольку все три вышеописанных подхода привлекательны с определенных точек зрения, было предпринято немало попыток соотнести их друг с другом. Рудольф Карнап разработал формальную теорию согласованной системы приобретения нового знания, основанную на байесовском подходе, в которой совмещаются объективный и субъективный подходы. Гленн Шэфер подошел к объединению этих подходов с другой стороны – посредством формального различения разных типов вероятностей, делая упор на принципиальное отличие вероятности случайных событий от степени убежденности в наступлении тех или иных событий. Эта последняя концепция является основополагающей для субъективизма, четвертой традиции, о которой следует упомянуть.
Субъективная, или персоналистская доктрина вероятности изначально разрабатывалась Фрэнком Рамсэем, Бруно де Финетти, Леонардом Сэвиджем и Праттом, Райффой и Шлайфером. С их точки зрения вероятности – это степени убежденности в том, что наступят те или иные события – как повторяющиеся, так и уникальные (например, третья мировая война). Данному множеству гипотез в принципе можно приписать любые субъективные вероятности при соблюдении некоторых условий рациональности. В отличие от других доктрин, эти условия рассматриваются здесь как достаточные и необходимые одновременно, без каких-либо дополнительных ограничений, накладываемых по логическим или эмпирическим соображениям. Основная аксиома совместимости
, принятая в теории субъективной вероятности, – это согласованность предпочтений. Эта аксиома означает, что вероятности элементарных событий дают в сумме единицу, и что взаимодополняющие и взаимоисключающие события следуют с вероятностью, равной соответственно произведению и сумме элементарных вероятностей. В этом свете субъективные вероятности с математической точки зрения ничем не отличаются от других типов вероятности. Субъективная школа выработала процедуру одновременного измерения полезности и вероятности, основанную на выявленных предпочтениях.
Как видим, вероятность – не такое уж простое понятие. Ее измерение, очевидно, – нелегкое дело даже в некоторых вероятностных играх, не говоря уже о реальном мире. Чтобы отличать субъективную вероятность от объективной, первую из них мы будем обозначать f
(p
). Преобразование f
() показывает, что вероятности, используемые в модели ожидаемой полезности, могут отличаться от установленных или тех, которые исследователь полагает объективными. Однако не все такие преобразования f
(pi
), обладающие свойствами вероятностей (таким, как Σf
(pi
) = 1), должны рассматриваться как степени убежденности в том, что события наступят. В литературе преобразования f
(pi
) обычно используются в качестве показателей отношения к риску; для исследования симметричности компонент вероятности и ожидаемого исхода в моделях ожидаемой полезности; чтобы отразить предпочтения в отношении вероятностей и/или дисперсий, наконец, просто чтобы эмпирические данные можно было согласовать с предпосылкой нелинейности предпочтений по вероятности. Хотя эти разнообразные модели, как правило, относят к теории субъективной ожидаемой полезности, преобразование f
(pi
) не обязательно должно являться мерой степени убежденности. Помимо преобразований, которые сохраняют математические свойства вероятности, существует много теорий, в которых это требование ослаблено. В Приложении Д эти преобразования вероятностей обозначены w
(pi
), – мы будем называть их весами решений. Причем веса решений – это не вероятности: по словам Дэниэля Канемана и Амоса Тверски, они не подчиняются аксиомам вероятностей, и не должны интерпретироваться как меры убежденности. В их теории перспектив веса решений вводятся для того, чтобы отразить влияние событий на общую привлекательность игр – поэтому они монотонны по вероятности, но не обязательно линейны.
Подводя итоги, можно отметить, что полезность и вероятность по-разному трактуются в моделях ожидаемой полезности. Теоретическая концепция этой своеобразной психологии риска прошла последовательно четыре этапа:
а) На первом этапесчиталось, что значение неопределенной перспективы равно придаваемому ей математическому ожиданию денежных значений выигрышей: 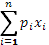 т.е. их средней, взвешенной по объективными вероятностям. т.е. их средней, взвешенной по объективными вероятностям.
б) На втором этапе стали учитывать психологические значения выигрышей, которые заменили денежные значения в предыдущей формуле. Тем самым было предложено выражение где p
i
– объективные вероятности, а 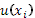 психологические значения в зависимости от исхода (выигрыша). Основными идеологами этой модели являются Бернулли, Нейман и Моргенштерн (разницей лишь в видах функции психологические значения в зависимости от исхода (выигрыша). Основными идеологами этой модели являются Бернулли, Нейман и Моргенштерн (разницей лишь в видах функции 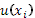 ). ).
в) На третьем этапебыла высказана идея, что индивид оперирует не объективными вероятностями, а психологическими представлениями о них, т.е. субъективными вероятностями. Так возникла формула –, где 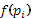 - субъективные вероятности. Эта формула остается еще вида формулы Бернулли, но объективные вероятности уже заменены субъективными. - субъективные вероятности. Эта формула остается еще вида формулы Бернулли, но объективные вероятности уже заменены субъективными.
г) На четвертом этапе, наконец, пришли к тому, что следует учитывать не только средневзвешенные по вероятностям психологические значения 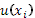 , но также и функцию распределения вероятностей, откуда следует формула , но также и функцию распределения вероятностей, откуда следует формула
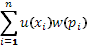 . .
В Приложении Д показаны основные модели ожидаемой полезности, существующие на данный момент. Основными различиями в моделях, как говорилось в начале параграфа, являются разновидности функций полезности и вероятности. Существуют и другие различия: например, в теории перспектив исходы xi
определяются как изменение финансового положения, а не итоговой величины богатства индивида. Кроме того, в описательных моделях пространство исходов может включать такие измерения, как сожаление, обоснованность выбора и т.д. Большинство из перечисленных моделей возникли как описательные, за исключением разве что моделей Неймана-Моргенштерна и Сэвиджа. Наверное, благодаря именно этому практическое использование закрепилось в основном за этими двумя моделями.
Как описательная модель, ориентированная на постижение процесса принятия решения, теория ожидаемой полезности несостоятельна по крайней мере с двух точек зрения.
Во-первых, люди не рассматривают все проблемы как единое целое, как это полагает теория ожидаемой полезности. При выборе в условиях неопределенности индивид физически не способен принимать в расчет все возможные исходы, потому что попросту не имеет информации о них.
Во-вторых, они не обрабатывают информацию, особенно вероятности, в соответствии с принципами ожидаемой полезности (существуют масса исключений в поведении людей, которые невозможно описать с помощью данных функций полезности или вероятности).
Помимо этого сложность вызывает построение функции полезности Неймана-Моргенштерна. Использование в качестве стандарта лотерей с вероятностью 50/50 зачастую приводит к иным функциям полезности, чем, например, при использовании лотерей с вероятностями 30/70. Установлено, что весьма незначительные изменения в контексте или общих условиях формулировки проблемы могут привести к совершенно иным предпочтениям. Таким образом, встает вопрос еще и о том, в каком из контекстов следует измерять "истинное" отношение к риску; или, в более фундаментальной постановке, существуют ли в действительности неизменные вкусы и предпочтения, которые были бы совместимы с аксиомами ожидаемой полезности.
Однако нет правил без исключений. Для хорошо структурированных повторяющихся ситуаций со значительными ставками, в которых решения принимают хорошо подготовленные специалисты, максимизация ожидаемой полезности может хорошо описывать действительный процесс принятия решения, – например, если речь идет о бурении нефтяных скважин. Действительно, в крупных организациях, где используются компьютеры и работают высококвалифицированные менеджеры, модель ожидаемой полезности может использоваться в явном виде. Однако даже в таких благоприятных условиях постановки проблем и их решения могут быть искажены, если учесть невозвратные издержки, эффекты изоляции, асимметричность оценок альтернативных и непосредственных издержек и прочие косвенные факторы.
И всё же если бы не было самой теории ожидаемой, большая часть вышеупомянутых исследований не имела бы место. Модель как таковая породила более глубокие идеи и поставила более тонкие вопросы как описательного, так и нормативного характера относительно принятия решений в условиях риска. Она выявила тот факт, что люди воспринимают и решают проблемы иначе, и предложила схему и язык, в рамках которых обсуждаются эти расхождения. Впрочем это не меняет того факта, что нынешний статус общепринятой концепции в некоторых областях применения может быть поставлен под вопрос. Тем не менее, пока не созданы более удачные модели рациональности, максимизация ожидаемой полезности, несомненно, может оставаться ценным ориентиром, с которым можно сравнивать и по которому можно корректировать реальное поведение. Вместе с тем, возможно, что нынешние парадоксы и устойчивые нарушения ожидаемой полезности содержат в себе семена будущих нормативных и описательных теорий выбора. В конце концов, ведь именно парадокс Бернулли породил нынешнюю модель ожидаемой полезности.
В предыдущем параграфе были рассмотрены основные модели общей полезности. Отличия в них по сути заключались в различных функциях психологических преобразований объективных переменных: вероятности и исхода рисковой ситуации. То есть многие экономисты пытались максимально отождествить формальную математическую функцию и поведение [рационального] человека.
Говоря о психологическом восприятии индивидуумом действительности (в нашем случае рисковой ситуации) принято рассматривать две отклоняющиеся от нормальной ситуации типологии поведения.
О первой, неприятии риска, было упомянуто еще в модели ожидаемой полезности Неймана-Моргенштерна. Именно в этой модели впервые принимается во внимание психологический эффект, производящий влияние на функцию полезности. Противником риска считается человек, который предпочитает рисковой ситуации результат, равный ожидаемому значению исходов. Это означает, что для этого человека полезность ожидаемого дохода больше ожидаемой полезности рисковой ситуации. Иначе говоря, если такому человеку предложить одно из двух: либо 10 рублей, либо 5 рублей с вероятностью 50% и 15 рублей с вероятностью 50%, - то он выберет 10 рублей и избежит рисковой ситуации. То есть 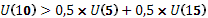 . Графически эта ситуация изображена в Приложении Е. Выпуклая вверх функция – кривая полезности для индивида, который не является сторонником риска. Причем существует прямо пропорциональная зависимость между степенью неприятия и выпуклостью функции. Для такого вида функции производная первого порядка . Графически эта ситуация изображена в Приложении Е. Выпуклая вверх функция – кривая полезности для индивида, который не является сторонником риска. Причем существует прямо пропорциональная зависимость между степенью неприятия и выпуклостью функции. Для такого вида функции производная первого порядка 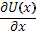 будет убывающей величиной. Каждое равное увеличение дохода будет порождать всё меньшие увеличения полезности (это видно на графике). будет убывающей величиной. Каждое равное увеличение дохода будет порождать всё меньшие увеличения полезности (это видно на графике).
Стоит отметить, что для определения степени неприятия риска (степени выпуклости вверх функции U(x)) был введен коэффициент Эрроу-Пратта (независимо друг от друга Arrow, 1971 и Pratt, 1964). Он представлен в Приложении З. Являясь константой для линейных и экспоненциальных функций, этот коэффициент отражает важный момент – психологическое восприятие рисковой ситуации (неприятие, предпочтение) не зависят от исходов (результатов).
Что же касается уже упомянутой ситуации предпочтения риска, то она обратна вышеописанному случаю. То есть психологическое восприятие рисковой ситуации таково, что функция полезности такового индивида принимает вид выпуклой вниз экспоненциальной функции. В той же рисковой ситуации (Приложение Ж) полезность ожидаемого дохода U(10) будет ниже ожидаемой полезности этой рисковой ситуации 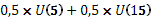 , что будет толкать индивида идти на риск. Для этого вида функции U(x) производная первого порядка , что будет толкать индивида идти на риск. Для этого вида функции U(x) производная первого порядка 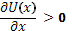 . Это означает, что с каждым одинаковым увеличением дохода полезность будет увеличиваться всё больше и больше. Теоретически коэффициент Эрроу-Пратта можно использовать и для ситуации предпочтения риска. . Это означает, что с каждым одинаковым увеличением дохода полезность будет увеличиваться всё больше и больше. Теоретически коэффициент Эрроу-Пратта можно использовать и для ситуации предпочтения риска.
На практике восприятия или отношение к риску можно увидеть воочию. Например, в ситуации выбора способа заработка. Бόльшая часть населения стран с рыночной экономикой пытаются найти такие положения, при которых в наименьшей степени возможно снижение уже имеющегося благосостояния. Поэтому эта же бόльшая часть населения предпочитает относительно стабильный заработок наемного работника ненадежному предпринимательскому доходу.
Основная причина этого состоит в том, что высокие прибыли, которые сулит частное предпринимательство, никто не гарантирует. И, отдавая свои предпочтения стабильным заработным платам, более низким, чем возможные прибыли предпринимательской деятельности, индивидуумы имеют возросшие альтернативные издержки. Можно сказать, что такие издержки идут на уменьшение риска.
Конечно, нельзя назвать такое поведение нерациональным. В условиях постоянных расходов для многих стабильность доходов является высшим приоритетом, которым нельзя пожертвовать ради увеличения богатства в будущем. В России эта ситуация подкрепляется еще и не самыми благоприятными условиями для предпринимательства, по разным оценкам, заключающимися в высокой степени нестабильности.
Но избежание или приятие риска не являются единственными действиями, которые возможно, а порой даже необходимо производить над рисковыми ситуациями и неопределенностью.
Еще Ф. Найт утверждал, что в человеке наблюдается постоянное стремление избавиться от любого вида неопределенности. «…при рациональном поведении имеет место стремление свести к минимуму неопределенности, связанные с приспособлением средств к целям[8]
». Но это, как ни парадоксально, не означает, что наше стремление имеет окончание в точке полного избавления от неопределенности, даже если это и невозможно. Вряд ли кто-либо пожелал бы в условиях абсолютной детерминации. Тем не менее какая-то сила заставляет нас гнаться за тем, что нам не нужно и недостижимо. Можно сказать, тут раскрывается один из диалектических законов - единство и борьба противоположностей.
Как бы то ни было, стремления так или иначе повлиять на степень неопределенности и риска присутствуют на практике. Рассмотрим некоторые из их разновидностей.
Снова возвращаясь к работе Ф. Найта, заметим, что он выделяет два принципиальных способа снижения неопределенности, основанные на двух ключевых моментах. «…наиболее существенные точки зрения, связанные с неопределенностью, суть, во-первых, возможность уменьшить её масштаб путем группировки случаев, а во-вторых, разное отношение индивидов к неопределенности, порождающее тенденцию к сосредоточению функции ее преодоления в руках определенных индивидов или классов[9]
». Если классифицировать единичные исходы по группам, то степени неопределенности будут меньше, чем если эти случаи рассматривать в отдельности. При априорной вероятности неопределенность исчезает с размером группы. Например, вероятность выпадения хотя бы одного герба из одной, двух, трех монет увеличивается по мере роста числа монет в испытании. Та же закономерность наблюдается и в статистической вероятности, но не так явно, ибо нет такой же однородности групп.
Среди способов снижения неопределенности, основанных на этом принципе, можно выделить следующие:
Диверсификация – это метод, направленный на снижение риска путем распределения его между несколькими рисковыми товарами таким образом, что повышение риска от продажи/покупки одного означает понижение риска продажи/покупки другого. Например, диверсификацией риска считается случай, когда одна фирма, выпускающая товары военного и мирного применения одновременно, имеет сбалансированный рост объема продаж одного из видов продукции соответственно в войну и в мирное время.
Объединение риска – это метод, направленный на снижение риска путем превращения случайных убытков в относительно небольшие постоянные издержки. Этот принцип лежит в основе страхования. Постоянные издержки – стоимость страховки. Риск, в случае негативного исхода, компенсируется выплатой по страховке.
Поиск информации так же является довольно действенным методом, так как воздействует на саму причину возникновения неопределенности – недостаток информации. Получение информации может значительно снизить степень неопределенности и даже может трансформировать ее из неизмеримой в измеримую, то есть риск.
Вторым принципом, на котором основаны способы снижения вероятности, является распределение неопределенности между лицами, готовыми с ней «справляться». Сюда относятся следующие способы.
Распределение риска – это метод, при котором риск вероятного ущерба делится между участниками таким образом, что возможные потери каждого относительно невелики. Именно поэтому крупные ФПГ не боятся идти на риск финансирования крупных проектов или новых направлений НИОКР.
Существенным методом в рамках этой группы способов являются спекуляции. Спекуляция – деятельность, выражающаяся в покупке с целью перепродажи по более высокой цене. Спекулянты, таким образом, играют роль посредником между теми, кто обладает благом, и теми, кто в нем нуждается. Удастся ли перепродать благо дороже в будущем? Таких гарантий никто не даст. Поэтому спекулянты рискуют, нередко расплачиваясь за риск собственным благосостоянием. Они покупают риск у тех людей, которые не склонны рисковать, в надежде получить прибыль.
Кроме двух вышеупомянутых принципов снижения неопределенности, можно так же выделить такие немаловажные, как управление будущим и повышенная способность к прогнозированию. На межорганизационном уровне фирмы заключают между собой разные виды контрактов, давая друг другу гарантии, выполняя обоюдные обязательства, неся ответственность. Это уменьшает риски поведенческого характера.
Существуют еще множество способов влияния в той или иной степени на риск. Выше же были рассмотрены принципиально основные из них.
Заключение по Главе 1.
Данная глава работы представляет собой попытку обобщения и систематизации концепции риска и неопределенности и выбора в условиях риска и неопределенность. Вначале были приведены основные точки зрения на определениях этих понятий, что позволило в некоторой степени систематизировать понятийный аппарат теории, что явилось своеобразным базисом для дальнейших исследований. В рамках классификации были приведены основные виды рисков.
Кроме того, в последующих параграфах были, по возможности, упомянуты основные модели ожидаемой полезности, способы измерения вероятностей и психологические аспекты при выборе в условиях риска и неопределенности. Сама теория ожидаемой полезности является идеологическим ядром концепции выбора в условиях риска неопределенности (по крайней мере пока ей не найдется адекватная замена). Были намечены основные дискуссионные вопросы в рамках исследуемой проблемы, а так же границы применимости на практике.
В заключительном параграфе, рассматривающем основные способы снижения риска, можно отметить максимальную приближенность к практике и актуальность.
Таким образом, проблема выбора в условиях неопределенности была разбита на 6 подтем, каждая из которых была в известной степени освещена. В дальнейшем они могут послужить целостным инструментом при решении этой проблемы выбора.
В данной главе мы постараемся рассмотреть, как влияют риски и неопределенность на рынок активов. Установим связь между доходностью актива и степенью риска.
Активы – это средства, обеспечивающие денежные поступления в форме как прямых выплат (прибыль, дивиденды, рента и т. д…), так и скрытых выплат (увеличение стоимости фирмы, недвижимости, акций и т.д…). Рисковые активы – это активы, доход от которых частично зависит от случая.[10]
Инвестор, оперирующий на финансовом рынке, где цены бумаг (например, облигаций, акций) колеблются непредсказуемым образом, вынужден принимать решения в условиях риска. Одна из наиболее известных задач в таких условиях – задача формирования инвестиционного портфеля (набора) из различных ценных бумаг. Допустим, у инвестора имеется информация о колебании цен в прошлом. Как инвестору обработать эту информацию, чтобы принять правильное решение?
Математическое ожидание (среднее значение) – наиболее простой и естественный критерий выбора в ситуациях, когда будущие поступления/потери случайны. Это также исторически самый первый критерий. Если бы инвестор действовал по правилу максимального среднего, он мог бы выбрать для инвестирования ценную бумагу с наибольшей доходностью, оцененной по данным за определенный период времени, возможно, с поправкой на будущее состояние рынка.
Такой выбор, однако, не учитывает риска возможных случайных колебаний доходностей вокруг среднего. А в условиях неопределенности это весьма важно. Поэтому широкое распространение в теории и на практике получило использование дисперсии в качестве показателя риска. Пример выбора, основанного на измерении риса дисперсии, дает так называемая модель оценки фондовых активов (capitalassetspricingmodel – CAMP). Мы рассмотрим её лишь в самых общих чертах, преимущественно с точки зрения принципов сравнения и выбора альтернатив в условиях риска.
Теория CAMPвозникла как развитие теории выбора портфеля Марковица. Марковиц ввел принцип сравнения по среднему и дисперсии, который в общем можно сформулировать так. Если рассматривать альтернативы, характеризующиеся случайными величинами, то принцип сравнения по среднему и дисперсии заключается в том, что из двух случайных величин «лучшей» считается величина, имеющая большее среднее и меньшую дисперсию.[11]
Стоит отметить, что в этой формулировке скрыто подразумевающее и свойственное людям неприятие риска, а если точнее – стремление к наименьшему риску.
В модели средней и дисперсии относительно нее предполагается, что полезность распределения вероятностей, приносящего инвестору богатство 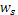 с вероятностью с вероятностью 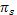 , можно выразить как функцию средней данного распределения и дисперсии относительно этой средней, , можно выразить как функцию средней данного распределения и дисперсии относительно этой средней, 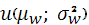 , где , где 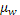 - математическое ожидание богатства, - математическое ожидание богатства, 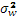 - его дисперсия. Или, если это более удобно, полезность можно выразить в виде функции средней и стандартного отклонения, - его дисперсия. Или, если это более удобно, полезность можно выразить в виде функции средней и стандартного отклонения,  , где , где 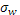 - среднее квадратичное отклонение. Поскольку и дисперсия, и стандартное отклонение есть меры степени риска, характеризующей распределение вероятностей, можно считать полезность зависящей от любого из этих двух показателей. - среднее квадратичное отклонение. Поскольку и дисперсия, и стандартное отклонение есть меры степени риска, характеризующей распределение вероятностей, можно считать полезность зависящей от любого из этих двух показателей.
Эту модель можно рассматривать как упрощение модели ожидаемой полезности, описанной в предыдущей главе. Если существует возможность полностью охарактеризовать варианты производимого выбора с помощью соответствующей им средней и дисперсии относительно нее, то на основе функции полезности для средней и дисперсии можно ранжировать варианты выбора таким же образом, как и на основе функции ожидаемой полезности. Но это так только в первом приближении.
Модель средняя - квадратичное отклонение применяется в простейшей задаче об оценке портфеля, содержащего различные ценные бумаги. В данной работе рассмотрим портфель, состоящий из двух ценных бумаг. Одна из них будет приносить фиксированный доход - 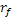 . Это – безрисковый актив. Такими активами являются надежные (в основном государственные) облигации. . Это – безрисковый актив. Такими активами являются надежные (в основном государственные) облигации.
Другой актив - это рисковый актив. Доход по нему непостоянен во времени и зависит от многих факторов, в том числе конъюнктуры на рынке. Тогда 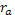 - доход на этот актив при исходе a, а - доход на этот актив при исходе a, а 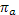 - вероятность наступления данного исхода. При этом - вероятность наступления данного исхода. При этом 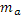 - ожидаемый доход на рисковый актив, а - ожидаемый доход на рисковый актив, а 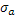 - стандартное отклонение дохода. - стандартное отклонение дохода.
Если обозначить через х долю средств, вложенных в рисковый актив, и соответственно (1-х) – в безрисковый актив, то ожидаемый доход на весь портфель будет задан формулой:
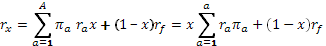
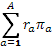 = = 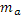 , ожидаемый доход на рисковый актив. Подставив, получим , ожидаемый доход на рисковый актив. Подставив, получим
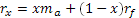
Таким образом, ожидаемый доход на портфель из двух активов есть среднее арифметическое взвешенное двух ожидаемых доходов. Если же портфель состоит из N активов, то ожидаемый доход представится так:
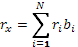
, где 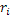 - доходность одного активна, - доходность одного активна, 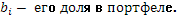
Дисперсия портфельного дохода задана формулой
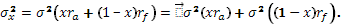
Так как  дисперсия портфельного дохода будет равняться дисперсии значений рискового актива, взвешенной в ее доле. дисперсия портфельного дохода будет равняться дисперсии значений рискового актива, взвешенной в ее доле.
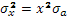
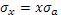 , , 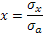
Если подставить х в уравнение ожидаемого дохода, то получится равенство
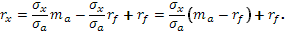
Естественно предположить, что 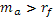 , так как инвестор, не расположенный к риску, никогда не будет держать в своем портфеле рисковый актив, если он приносит более низкий ожидаемый доход, чем безрисковый актив. Отсюда следует, что если направить большую долю своего богатства на покупку рискового актива, то получится более высокий ожидаемый доход, но также при довольно большом риске. Это изображено возрастающими прямыми в приложении К. , так как инвестор, не расположенный к риску, никогда не будет держать в своем портфеле рисковый актив, если он приносит более низкий ожидаемый доход, чем безрисковый актив. Отсюда следует, что если направить большую долю своего богатства на покупку рискового актива, то получится более высокий ожидаемый доход, но также при довольно большом риске. Это изображено возрастающими прямыми в приложении К.
Если выбрать x=1
, то это означает, что все деньги будут вложены в рисковый актив, ожидаемый доход и стандартное отклонение будут равняться (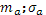 ). Если x=0
, все инвестиции будут вложены в надежный актив и ожидаемые доход и стандартное квадратичное отклонение будут равняться ( ). Если x=0
, все инвестиции будут вложены в надежный актив и ожидаемые доход и стандартное квадратичное отклонение будут равняться (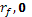 ). Ожидаемая доходность портфеля А, состоящего и из безрискового и из рискового активов, будет равняться ). Ожидаемая доходность портфеля А, состоящего и из безрискового и из рискового активов, будет равняться
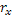 = = 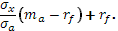 Причем значения доходности будут лежать на АВ, в зависимости от x. Причем значения доходности будут лежать на АВ, в зависимости от x.
Если на этом графике представить каждый возможный рисковый актив с определенной доходностью с помощью параметров 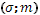 , то это множество будет выпуклым вверх. Причем верхняя граница этого множества будет представлять собой границу, на которой находятся самые эффективные активы – т. е. будет соблюдаться принцип сравнения по среднему и дисперсии. В приложении К эта линия - Е – утолщена. Она называется границей эффективности. , то это множество будет выпуклым вверх. Причем верхняя граница этого множества будет представлять собой границу, на которой находятся самые эффективные активы – т. е. будет соблюдаться принцип сравнения по среднему и дисперсии. В приложении К эта линия - Е – утолщена. Она называется границей эффективности.
Если отметить на границе такую точку М, что ВМ – касательная к границе эффективности, это будет означать, что ВМ – наиболее эффективная бюджетная линия
. Для любой точки отрезка АВ можно указать точку отрезка ВМ, лежащую выше нее. В точке касания бюджетной линии и границы эффективности будет достигаться удовлетворение – т. е. оптимальное сочетание безрискового и рискового активов. Такое сочетание называется оптимальной комбинацией рисковых активов, а соответствующий портфель называется рыночным.
Наклон бюджетной линии называются рыночной ценой риска. То есть
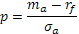
Она показывает, на сколько повышается риск портфеля на единицу прироста средней доходности.
Так что же можно сказать о применимости среднего квадратичного отклонения и среднего в качестве меры риска? Во всяком случае, это мера хорошо «работает», когда распределение случайных величии близко к нормальному. Но в свою очередь нормальное распределение в случайных экономических процессах встречается далеко не всегда. Поэтому в некоторых случаях это модель может оказаться совершенно неприемлемой. Например, дисперсия явно плохая характеристика риска для ассиметричных распределений или для распределений дискретных случайных величин.
Способы измерения величины рисков в рисковых активов отличаются в ситуациях, когда имеется один портфель или несколько.
Для ситуации с несколькими портфелями было найдена зависимость между величиной риска в одном активе и величинами рисков в других активах. Иными словами величина риска, характеризующая данный актив, зависит от его корреляции с другими активами. Поэтому меру риска акции измеряют относительно уровня риска по всему фондовому рынку:
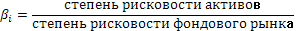
Оценку беты акций позволяют получить статистические методы, определяющие степень чувствительности одной переменной доходности акции по отношению к другой, и существует много консультационных инвестиционных служб, способных предоставить оценки беты конкретных видов акций.
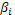 используется в качестве поправки на риск. Если в предыдущей формуле прибыльности портфеля, состоящего из безрискового и рискового активов, весами было используется в качестве поправки на риск. Если в предыдущей формуле прибыльности портфеля, состоящего из безрискового и рискового активов, весами было 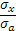 , то теперь весами будет отношение степени рисковости активов к степени рисковости всего рынка, то есть , то теперь весами будет отношение степени рисковости активов к степени рисковости всего рынка, то есть 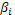 : :
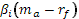 ; ;
Условие равновесия рисковых активов звучит так: в равновесии все активы должны приносить одинаковую, с учетом поправки на риск, норму дохода.
Если имеется два актива i
и j
с ожидаемыми доходами 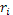 и и 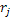 и бетами и бетами 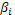 и и 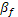 , то в равновесии должно удовлетворяться следующее условие: , то в равновесии должно удовлетворяться следующее условие:
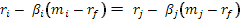
Для надежного актива, по определению, должно соблюдаться 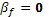 . Причина этого состоит в том, что риск по данному активу равен нулю, а . Причина этого состоит в том, что риск по данному активу равен нулю, а 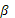 измеряет величину риска, характеризующую актив. Таким образом, для любого актива i
должно соблюдаться измеряет величину риска, характеризующую актив. Таким образом, для любого актива i
должно соблюдаться
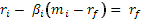 . .
После преобразований это уравнение говорит о том, что
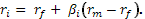
или что ожидаемый доход на любой актив должен равняться сумме дохода на надежный актив и поправки на риск.
Согласно модели, обрисованной выше, ожидаемый доход на любой актив должен быть равен доходу на надежный актив плюс премия за риск:
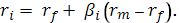
В приложении М изображен график данной функции, причем по оси ординат - 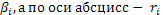 . Отталкиваясь от этой модели, все комбинации ожидаемого дохода и беты для активов, находящихся в равновесии, должны лежать на этой линии. Эта линия именуется линией фондового рынка. . Отталкиваясь от этой модели, все комбинации ожидаемого дохода и беты для активов, находящихся в равновесии, должны лежать на этой линии. Эта линия именуется линией фондового рынка.
Обрисуем ситуацию, при которой ожидаемы доход и бета не будут лежать на линии фондового рынка.
Ожидаемый доход на актив есть ожидаемое изменение его цены, деленное на его текущую цену: 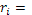 ожидаемое значение ( ожидаемое значение (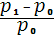 ). Причем р1
– случайная величина. ). Причем р1
– случайная величина.
Пусть найден такой актив, норма ожидаемого дохода на который, с поправкой на риск, выше нормы для безрискового актива:
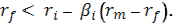
Вложение в этот актив оказывается очень выгодной сделкой. Оно приносит более высокую, с учетом поправки на риск, норму дохода, чем норма дохода на безрисковый актив.
Обнаружив, что такой актив существует, люди захотят купить его. Спрос на такой актив, безусловно, появится.
Однако, пытаясь купить данный актив, люди будут предлагать за него цену выше сегодняшней: p0
будет расти. Это означает, что ожидаемый доход ri
упадет. Насколько он упадет? Как раз настолько, чтобы вновь понизить ожидаемую норму дохода до уровня, соответствующего линии рынка.
Таким образом, покупка актива, лежащего над линией рынка, - выгодная сделка. Ведь когда люди обнаружат, что, при данном риске, он приносит более высокий доход, чем те активы, которыми они владеют в настоящий момент, они начнут предлагать за этот актив более высокую цену.
Все сказанное покоится на гипотезе о том, что люди не расходятся во мнениях относительно величины риска, характеризующей различные активы. Если мнения людей в отношении ожидаемых доходов или бет по различным активам расходятся, модель значительно усложняется.
Модель оценки фондовых активов может быть использована для сравнения различных инвестиций с точки зрения их риска и дохода на них. Одним из популярных видов инвестиций являются инвестиции во взаимный фонд. Взаимные фонды - это крупные организации, принимающие деньги у индивидуальных инвесторов и использующие эти деньги для покупки и продажи акций компаний. Прибыли, приносимые такими инвестициями, выплачиваются затем индивидуальным инвесторам.
Преимущество взаимного фонда состоит в том, что деньгами управляют профессионалы. Его недостаток заключается в том, что они берут плату за это управление. Однако обычно эта плата не бывает слишком высока, и для большинства мелких инвесторов совет вложить деньги во взаимные фонды является скорее всего разумным.
Но как выбрать тот взаимный фонд, в который стоит вложить деньги?
Один из путей, по которому можно пойти, заключается в том, чтобы взглянуть на данные о функционировании различных взаимных фондов в предыдущие периоды и подсчитать среднегодовой доход и бету - величину риска - для каждого из рассматриваемых вами взаимных фондов.
Если нанести на график ожидаемые доходы вдоль одной оси и беты вдоль другой, можно заметить линию тренда и получить график (приложение Н.) Конечно, взаимные фонды с высокими значениями ожидаемого дохода обычно характеризуются высоким риском. График, характеризующий взаимные фонды, имеет смысл использовать для сравнения стратегии инвестиций, осуществляемых с помощью профессиональных менеджеров, с очень простой стратегией вложения части денег в так называемый индексный фонд. Существует несколько индексов активности фондового рынка, таких, как индексы Доу-Джонса или индекс компании "Стэндард энд Пуурз" – S&P 500, и т.п. Каждый из этих индексов представляет собой, как правило, средний доход, рассчитываемый на заданный день для определенной группы акций. Индекс S&P 500, например, основан на средней доходности акций 500 компаний, котирующихся на Нью-Йоркской фондовой бирже. Российский индекс РТС рассчитывается на основе 50 ценных бумаг наиболее капитализированных российских компаний. Индекс ММВБ включает 30 наиболее ликвидных акций российских эмитентов входящих в список Фондовой биржи ММВБ.
Индексный фонд - это взаимный фонд, владеющий акциями компаний, на которых базируется подобный индекс. Это означает, что тому, кто инвестирует в этот фонд, буквально по определению, гарантируется получение средней доходности акций, включаемых в индекс. Поскольку удержаться на уровне средней доходности не очень трудно - по крайней мере, не так трудно, как попытаться ее превзойти, - гонорары менеджеров в индексных фондах, как правило, низки. Поскольку индексный фонд владеет очень широкой базой рисковых активов, его бета обычно очень близка к 1 - он несет такой же риск, как и рынок в целом, потому что индексный фонд владеет акциями почти всех компаний, действующих на рынке в целом.
Один из способов, которым можно на практике найти соотношение между индексным фондом и обычным, состоит в том, чтобы нанести на график ожидаемый доход и бету фонда, базирующегося на каком-нибудь индексе, и провести линию, соединяющую соответствующую точку с нормой дохода для безрискового актива. На этой линии можно получить любую комбинацию риска и дохода - для этого надо просто решить, сколько денег надо вложить в безрисковый актив, а сколько - в индексный фонд.
Для выявления закономерности подсчитаем число взаимных фондов, оказавшихся под этой линией. Это - взаимные фонды, предлагающие такие комбинации риска и дохода, которые хуже комбинаций, получаемых при вложении "индексный фонд/безрисковый актив". Когда вы это проделаете, окажется, что подавляющее большинство комбинаций, предлагаемых взаимными фондами, находится под указанной линией. Число фондов, нанесенных выше этой линии, не превышает того, которого можно было бы ожидать согласно теории вероятности.
Если, однако, взглянуть на это открытие с другой стороны, то оно, возможно, не покажется столь уж удивительным. Фондовый рынок - чрезвычайно конкурентная среда. Люди все время пытаются найти акции, курс которых в данный момент занижен, с тем, чтобы их купить. Это означает, что, в среднем, акции продаются по цене, соответствующей тому, чего они стоят в действительности. А если это так, то делать ставку на средний уровень дохода и риска - стратегия весьма разумная, так как превзойти средние показатели практически невозможно.
Заключение по Главе 2.
В данной главе были рассмотрены основной подход к оценке рисковых активов, а именно модель среднее - стандартное отклонение. Причем были приведены и доводы за использование этой и модели, и против для освещения различных точек зрения.
Помимо этого была затронута тема равновесия рисковых активов, установлено условие равновесия.
Наконец рассматривалось совокупное «поведение» рисковых активов на рынке. Для этого использовались инструменты выравнивания доходности, а так же линия фондового рынка.
Кроме всего прочего стоит отметить особую прикладную значимость этой главы. Если значение первой главы в основном теоретическое, то второй – практическое.
В итоге три параграфа, из которых состоит глава, помогают разобраться с проблемой оценки рисковых активов.
В последней главе работы приведено исследование понятие рискового актива, измерения его стоимости, а так же равновесия. Разумеется, подход к этой проблеме не ограничивается только этими концепциями, но, приведенные выше, они являются, на мой взгляд, наиболее распространенными и отчасти базовыми. Несомненно то, что результаты исследования показали основные способы и методы преодоления проблем на практике, поэтому исследования можно считать актуальными.
Особо стоит отметить, на мой взгляд, то, что вторая глава, хоть и носит теоретический характер, как и первая, но всё же имеет меньше идеологических затруднений, парадоксов и дискуссионных тем. Это связано, прежде всего, со степенью теоретического охвата исследований. Конечно, первая глава исследует фундаментальные теоретические проблемы риска и неопределенности, в то время как вторая – теоретические проблемы прикладного характера, а именно рисковые активы в условиях риска и неопределенности.
Всё же говоря о проделанной работе в целом, хочется отметить немалую актуальность темы. Возрастающий интерес среди как экономистов, так и социологов, к проблемам риска и неопределенности в 20-21 веке говорит сам за себя. Ведь именно на 20 век пришлось бурное исследование этой проблемы. В начале века появляются теоретические концепции риска и неопределенности, сочетающие в себе и философские, и психологические, и экономические методы. Так же с начала 20 века наблюдается активное исследование проблем поведения человека в условиях риска и неопределенности. Одна из концепций была приведена в данной работе – теория ожидаемой полезности. Анализ этой проблемы дал понять и выявление очень большего количества противоречий и разногласий, дает понять, насколько трудна для изучения эта проблема. Насколько глубоки и фундаментальны явления риска и неопределенности. В какой степени они внедряются в нашу повседневную жизнь, какое имеют влияние.
И безусловно, находясь в прямо пропорциональной зависимости от уровня развития информационного общества, эти явления, возможно, лишь «набирают оборот». Но наука не стоит на месте. Конечно, во многих моментах модели и концепции экономической теории далеки от реальности (например, модель ожидаемой полезности Неймана – Моргенштерна). Но не стоит забывать, когда-то и такие фундаментальные науки, как физика, были молодыми и неизученными.
Напоследок хотелось бы вспомнить вскользь упомянутый факт. Человек стремится к недостижимому – устранению неопределенности. И, может, именно этот недостижимый идеал заставляет его быть в вечном поиске.
Список литературы.
1. Алле М. Поведение рационального человека в условиях риска: критика постулатов и аксиом американской школы // THESIS. – 1994. - № 5. - с. 217-241.
2. Вэриан Х. Р. Микроэкономика. Промежуточный уровень. Современный подход. - М.:ЮНИТИ, 1997.
3. Гришаев В.В. – «Риск и общество (дискуссия о понятии риска и библиография)».
4. Луман Н. Понятие риска // THESIS. — 1994. — № 5. — с. 135—160.
5. Микроэкономика: практический подход (ManagerialEconomics): учебник/ кол. Авторов; под ред. А.Г. Грязновой , А.Ю. Юданова. – 4-е изд., перераб. И доп. – М.: КНОРУС, 2008. – 704 с.
6. Найт Ф.Х. «Риск, неопределенность и прибыль» / Пер. с англ. – М.: Дело, 2003. – 360. с .
7. Нейман Дж. фон, Монгерштерн О. Теория игр и экономическое поведение / Пер. с англ. - М.: Экономика, 1970. - 572 с.
8. Нуреев Р. М. Курс микроэкономики: учебник / Р. М. Нуреев. – 2-е изд., изм. – М.: Норма, 2008. – 576 с.
9. Салин В Н , Медведев В Г Понятие рисков и управления ими, методология оценки // Вестник Финансовой Академии. – 2004. - № З. – с. 29 - 43.
10. Салин В.Н., Медведев В.Г. Понятие рисков и управления ими; методология оценки. //Вестник Финансовой академии. 2004. № 3. С. 28-41.
11. Тэпман Л.Н. «Риски в экономике» / Под ред. проф. В.А. Швандара. М.: ЮНИТИ-ДАНА, 2002.- 380 с.
12. Фридмен М. Анализ полезности при выборе среди альтернатив, предполагающих риск // Теория потребительского поведения и спроса. СПб. - 1993. - с. 208-249.
13. Шапкин А.С., Шапкин В. А. «Теория риска и моделирование рисковых ситуаций». – М.: Издательско-торговая корпорация «Дашков и Ко
», 2005 – 880с.
14. Шестовских Т.С.Риск в структуре экономического поведения // Социологические исследования. - 1998. - № 5. - с. 116-119.
15. Шоломицкий А.Г. Теория риска. Выбор при неопределенности и моделирование риска. -М.: ИД ГУ-ВШЭ, 2005. - 400 с.
16. Шумейкер П. Модель ожидаемой полезности: разновидности, подходы, результаты, пределы возможностей// THESIS. – 1994. – Вып.5. – с. 29-80.
17. Kenneth J. Arrow. Risk Perception in Psychology and Economics // Economic Inquiry, January 1982, v.20, no.1, p.1–9.
Приложение А.
Пример классификации рисков.
 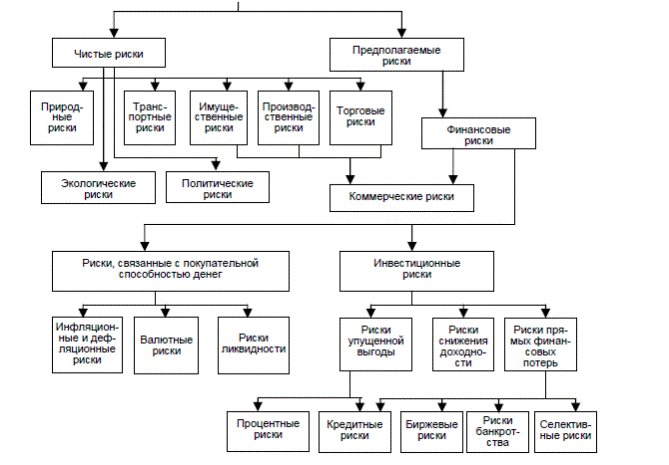
Приложение Б.
Математическое ожидание.
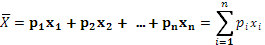 математическое ожидание. математическое ожидание. 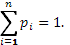
Приложение В.
Дисперсия.
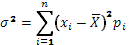 ; ; 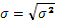 . .
Приложение Г.
Функция полезности Бернулли.
Функция, предложенная Бернулли, имела вид U
(x
) = b*
ln[(a
+x
)/a
]. Заметно, что производная первого порядка dU
(x
)/dx
= b
/(a
+x
) обратно пропорциональна богатству. Кроме того, производная второго порядка d2
U
(x
)/dx
2
< 0
Приложение Д.
Модели ожидаемой полезности.
| 11. |
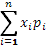 |
Ожидаемый денежный выигрыш. |
| 22. |
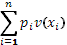 |
Бернуллианская ожидаемая полезность. (Бернулли, 1738) |
| 33. |
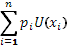 |
Ожидаемая полезность Д. Неймана и О. Моргенштерна, (1970). |
| 44. |
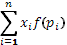 |
Теория достоверных эквивалентов (Schneeweiss, 1974; Handa, 1977, de Finetti, 1937). |
| 55. |
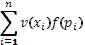 |
Субъективная ожидаемая полезность (Edwards, 1955). |
| 66. |
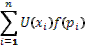 |
Субъективная ожидаемая полезность (Ramsey, 1931; Savage, 1954; Quiggin, 1980). |
| 77. |
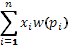 |
Взвешенный денежный выигрыш. |
| 88. |
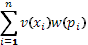 |
Теория перспектив (Kahneman and Tversky, 1979). |
| 99. |
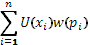 |
Субъективная взвешенная полезность (Karmarkar, 1978). |
| 110. |
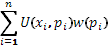 |
Lynch, 1979; Lehner, 1980. |
Приложение Е.
Модель неприятия риска.
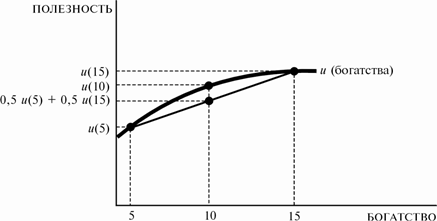
Приложение Ж.
Модель предпочтения риска.
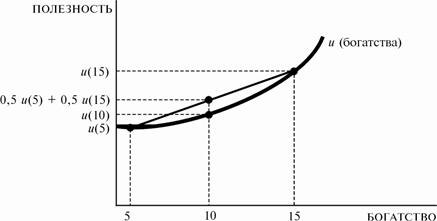
Приложение З.
Коэффициент Эрроу-Пратта.
Коэффициент Эрроу-Пратта 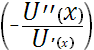 , где , где 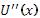 – производная U(x) второго порядка, а – производная U(x) второго порядка, а 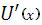 - первого. Эта мера не зависит от линейных преобразований функций, и имеет постоянное значение для линейных и экспоненциальных функций полезности. - первого. Эта мера не зависит от линейных преобразований функций, и имеет постоянное значение для линейных и экспоненциальных функций полезности.
Приложение К.
Риск и доход.
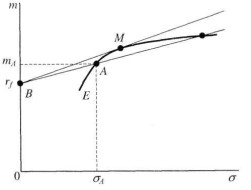
Бюджетная линия показывает издержки получения большего ожидаемого дохода, выраженные через возросшее стандартное отклонение дохода. В точке оптимального выбора кривая безразличия должна касаться бюджетной линии.
Приложение М.
Линия фондового рынка.
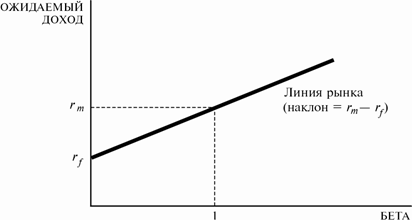
Линия рынка показывает комбинации ожидаемого дохода и беты для активов, находящихся в равновесии.
Приложение Н.
Взаимные фонды.
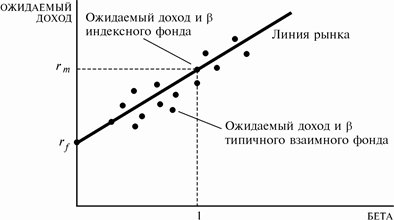
[1]
Санкт-петербургский парадокс (названный так, поскольку работа Бернулли появилась в Комментариях Санкт-Петербургской Академии) заключается в следующем: монета подкидывается n раз до тех пор, пока не выпадет "орел"; затем выплачивается 2 в степени n дукатов. Парадоксально, но математическое ожидание выигрыша представляет собой бесконечно большую величину, хотя здравый смысл приводит к заключению, что справедливым вознаграждением за участие в игре должна быть ограниченная сумма.
[2]
Найт Ф. Х. Риск, неопределенность и прибыль / Пер. с англ. – М.: Дело. 2003. с. 225-230.
[3]
Найт Ф. Понятия риска и неопределенности // THESIS. - 1994. - Вып. 5. С. 26.
[4]
В.Н. Салин, В.Г. Медведев. Понятие рисков и управления ими; методология оценки. //Вестник Финансовой академии. 2004. № 3. С. 28-41.
[5]
Найт Ф.Х. «Риск, неопределенность и прибыль» / Пер. с англ. – М.: Дело, 2003. -210 с.
[6]
Дж. фон Нейман, О. Моргенштерн «Теория игр и экономическое поведение». М.: Наука, 1970. – С.47.
[7]
Шумейкер П. Модель ожидаемой полезности: разновидности, подходы, результаты, пределы возможностей// THESIS. – 1994. – Вып.5. – с. 32-37; Фридмен М. Анализ полезности при выборе среди альтернатив, предполагающих риск // Теория потребительского поведения и спроса. СПб. - 1993. - с. 208-249.
[8]
Найт Ф.Х. «Риск, неопределенность и прибыль» / Пер. с англ. – М.: Дело, 2003. С. 230.
[9]
Там же.-С. 235
[10]
Нуреев Р. М. Курс микроэкономики: учебник / Р. М. Нуреев. – 2-е изд., изм. – М.: Норма, 2008. – С.400-401.
[11]
Шоломицкий А.Г. Теория риска. Выбор при неопределенности и моделирование риска. -М.: ИД ГУ-ВШЭ, 2005. – С.51.
|