| ФЕРРОМАГНИТНЫЙ МАТЕРИАЛ НА ОСНОВЕ
ZnSiAs
2
Перспективным направлением твердотельной электроники становится спинтроника, где, наряду с зарядом, спин электрона рассматривается как активный элемент для хранения и передачи информации. Ключевая проблема спинтроники – поиск и синтез новых ферромагнетиков, которые совместимы с «кремниевой технологией», имеют высокую температуру Кюри и способны инжектировать высокоподвижные поляризованные по спину носители тока [1]. В работах [2-4] путём введения в CdGeAs2
, CdGeP2
, ZnGeAs2
и ZnSnAs2
марганца удалось создать ферромагнетики с температурой Кюри выше комнатной. Для выбора оптимальных условий синтеза ZnSiAs2
, на основе анализа бинарных фазовых диаграмм Zn-As, Si-As, Si-Zn [5], проведена триангуляция тройной системы Zn-Si-As. Наиболее вероятные квазибинарные разрезы – Si-ZnAs2
, Zn-SiAs2
, в которых образуется тройное конгруэнтно плавящееся соединение ZnSiAs2
с Тпл
=10960
С [6].
Исходя из анализа тройной системы Zn-Si-As, синтез ZnSiAs2
с Mn проводили по разрезу ZnAs2
–Si, непосредственным сплавлением порошков Si и ZnAs2
с общим содержанием примесей ~10‑4
масс.% с добавлением в шихту высокочистого порошка марганца при температуре на 10-150
выше Тпл
ZnSiAs2
.
Гетероструктуры Si/ZnSiAs2
{Mn}, получали термической обработкой предварительно напылённых плёнок
ZnAs
2
и Mn определённой толщины на монокристаллические подложки кремния. Термический отжиг проводили при температурах 900-10000
С в парах цинка и мышьяка. Отношение толщин плёнок ZnAs2
к Mn составляло 10:1. Общая толщина гетероструктур 3-6 мкм. Образование ZnSiAs2
проходило по реакции ZnAs2
+Si=ZnSiAs2
. После отжига граница раздела между кремнием и диарсенидом цинка-кремния в гетероструктуре была резкой из-за малой растворимости кремния в ZnSiAs2
.
Идентификацию образцов проводили с помощью РФА, рентгенофлуоресцентного микроанализа и сканирующего электронного микроскопа. Согласно РФА образцы состояли только из фазы
ZnSiAs
2
с параметрами а
= 5,6084; c
= 10,8816Å, что хорошо согласовывается с данными JCPDS. Из рентгенофлуоресцентного анализа установлено, что содержание Zn, Si и As в образцах соответствовало 28:12:60 масс.% т.е. 1:1:1,91, что было близко к стехиометрическому составу ZnSiAs2
. Содержание марганца было около 1 масс.%. На некоторых образцах наблюдались микронеоднородности, их примерный состав был 48-52, 27-28, 18-26 масс.% As, Zn и Si, что, по-видимому, соответствовало тройной эвтектике ZnSiAs2
-Si-SiAs. Из исследований электрических и магнитных свойств установлено, что объемные образцы высокоомные, обладают p-типом проводимости и являются ферромагнетиками с температурой Кюри выше комнатной.
Изучение гетероструктуры Si/ZnSiAs2
{Mn} проводили с помощью оптического микроскопа Epiquant и сканирующего электронного микроскопа. Фотографии структур до и после термической обработки представлены на рис.1 (а, б).
Рис. 1. Фотографии гетероструктуры Si/ZnSiAs2
{Mn} до (а) и после (б) термической обработки.
По данным рентгенофлуоресцентного анализа поверхность гетероструктуры примерно на 1/3 отвечала составу ZnSiAs2
, наблюдались и микровключения тройной эвтектики ZnSiAs2
-Si-SiAs и ZnAs2
. Лучшие результаты получены, при напылении марганца на плёнку ZnAs2
. Неоднородности удаляли путем проведения прецизионного травления поверхности гетероструктуры.
С помощью сканирующего электронного микроскопа установлено распределение элементов в центре гетероструктуры, соотношение Zn:Si:As было близко к 1:1:2, содержание марганца соответствовало ~ 1масс.% (рис. 2).
| 
|

|
| Рис. 2. Распределение элементов (Zn, Si, As, Mn) в центре гетероструктуры Si/ZnSiAs2
{Mn}.
|
Магнитные свойства гетероструктуры Si/ZnSiAs2
{Mn} исследовали с помощью СКВИД магнетометра в интервале температур от 4,2 до 300 К и горизонтальных торсионных весов с электромагнитной компенсацией в интервале температур от 300 до 650 К (рис. 3). Температурная зависимость электросопротивления определялась 4-х зондовым методом (рис. 4).
Из анализа температурной зависимости намагниченности гетероструктуры Si/ZnSiAs2
{Mn} при напряжённости магнитного поля 6кЭ в интервале температур от 4,2 до 650 К установлено, что переход из ферромагнитного состояния в парамагнитное состояние происходит при температурах значительно выше комнатных. Температурная зависимость электросопротивления гетероструктуры характерна для вырожденного полупроводника.
| 
|

|
| Рис. 3. Намагниченность гетероструктуры Si/ZnSiAs2
{Mn}.
|
Рис. 4. Температурная зависимость электросопротивления гетероструктуры Si/ZnSiAs2
{Mn}.
|
Работа выполнялась при финансовой поддержке Российского фонда фундаментальных исследований 05-03-33068 и программы №8.5 по ОХМН РАН.
В антиферромагнитных (АФ) кристаллах эффект магнитного двулучепреломления (ДП) света определяется в основном теми магнитными вкладами в тензор диэлектрической проницаемости εαβ
, которые квадратичны по компонентам вектора АФ L
(слагаемые типа (Li
Lj)) (см.ссылки в [1-3]). В то же время, в присутствии магнитного поля В
, как показано в тех же работах, значительный вклад в эффекты ДП могут внести также магнитные вклады в компоненты тензора εαβ
вида (Li
Bj
). В исследуемом легкоплоскостном АФ α-Fe2
O3
(L
┴
С
3
), при перпендикулярном падении линейно-поляризованного света на образец вдоль тригональной оси С
3
существенную роль играют лишь те вклады, которые связаны с компонентами магнитного поля вдоль этой оси С
3
║Z
(слагаемые типа (Li
Bz
)) [1]. В этом случае распространяющиеся в образце нормальные оптические моды являются эллиптически поляризованными. Показатели преломления этих мод нелинейным образом зависят от компонент тензора диэлектрической проницаемости εxy
∞ Вz
(в системе осей координатX
║С
2
,Y
в плоскости базиса). Это должно привести к нелинейной зависимости от магнитного поля также и эффектов ДП [1,3]. Несмотря на подробное изучение явления магнитного ДП в АФ, особенно в гематите (см.ссылки в [1-3]), влияние на эффекты ДП вкладов, определяемых членами вида (Li
Bz
), изучалось не столь тщательно. В этой работе изложены результаты экспериментального исследования одного из аспектов данного вопроса, связанного, как будет показано ниже, с нарушением однородности магнитного поля в образце, приложенного в базисной плоскости (B
^С
3
), вдоль оси второго порядка С
2
.
Изучалось прохождение линейно поляризованного на входе света (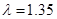 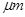 ), перпендикулярно падающего на образец вдоль оси С
3
(k
║С
3
, k
– волновой вектор света) в зависимости от величины В
и угла между направлением магнитного поля и направлением поляризации входящего света (f). Длина образцов вдоль оси С
3
составляла 0,057 и 0,62 cm. Эксперименты проводились с двумя значениями зазора электромагнита (13 и 50 mm). Магнитное поле контролировалось при помощи ЯМР-измерителя магнитной индукции. В первом случае (зазор 13mm.) поле было практически однородным во всем объеме образца. При этом z-компонента поля (Bz
) вдоль оси С
3
оказалась очень малой и можно было полагать Bz
» 0. При зазоре 50mm. магнитное поле имело неоднородность с градиентом до 3-4 mT/cm. Регистрировались зависимости угла поворота q плоскости поляризации света на выходе образца от угла f (для эллиптической поляризации выходящего света разность (f - q) определялась углом между большой полуосью эллипса и направлением В
). Измерения проводились при комнатной температуре. На Рис.1 приведены зависимости угла поворота q плоскости поляризации света на выходе из образца от угла f для более высокой (пуст. треуг.) и худшей (темн.треуг.) однородности магнитного поля В.
Как видно из Рис.1, в однородном магнитном поле зависимость в интервалах 0 - 40o
и 50о
- 90о
является линейной, неоднородность поля приводит к заметному отклонению от линейности. В экспериментах поляризация выходящего света менялась с изменением угла f: она линейная при f=0 и 90°, круговая при f = 45° и эллиптическая при промежуточных значениях. Это подтверждалось характером изменения интенсивности проходящего света от минимума при почти полном поглощении линейно поляризованного света скрещенными поляризаторами до максимума при круговой поляризации света на выходе из образца (Рис.1, темн. прямоуг). На Рис.2 представлена зависимость угла поворота q при фиксированном угле f = 22,50
от величины магнитного поля высокой однородности (пуст. прямоуг).
), перпендикулярно падающего на образец вдоль оси С
3
(k
║С
3
, k
– волновой вектор света) в зависимости от величины В
и угла между направлением магнитного поля и направлением поляризации входящего света (f). Длина образцов вдоль оси С
3
составляла 0,057 и 0,62 cm. Эксперименты проводились с двумя значениями зазора электромагнита (13 и 50 mm). Магнитное поле контролировалось при помощи ЯМР-измерителя магнитной индукции. В первом случае (зазор 13mm.) поле было практически однородным во всем объеме образца. При этом z-компонента поля (Bz
) вдоль оси С
3
оказалась очень малой и можно было полагать Bz
» 0. При зазоре 50mm. магнитное поле имело неоднородность с градиентом до 3-4 mT/cm. Регистрировались зависимости угла поворота q плоскости поляризации света на выходе образца от угла f (для эллиптической поляризации выходящего света разность (f - q) определялась углом между большой полуосью эллипса и направлением В
). Измерения проводились при комнатной температуре. На Рис.1 приведены зависимости угла поворота q плоскости поляризации света на выходе из образца от угла f для более высокой (пуст. треуг.) и худшей (темн.треуг.) однородности магнитного поля В.
Как видно из Рис.1, в однородном магнитном поле зависимость в интервалах 0 - 40o
и 50о
- 90о
является линейной, неоднородность поля приводит к заметному отклонению от линейности. В экспериментах поляризация выходящего света менялась с изменением угла f: она линейная при f=0 и 90°, круговая при f = 45° и эллиптическая при промежуточных значениях. Это подтверждалось характером изменения интенсивности проходящего света от минимума при почти полном поглощении линейно поляризованного света скрещенными поляризаторами до максимума при круговой поляризации света на выходе из образца (Рис.1, темн. прямоуг). На Рис.2 представлена зависимость угла поворота q при фиксированном угле f = 22,50
от величины магнитного поля высокой однородности (пуст. прямоуг).
Результаты измерений могут быть объяснены из следующих соображений. Согласно [1-3], при перпендикулярном падении (k
║С
3
) линейно поляризованного света в случае Bz
» 0 (малый зазор) нормальные оптические моды в образце также линейно поляризованы и угол поворота плоскости поляризации выходящего света (q) определяется выражением:
tg[2(f-q)] = cos2d×tg2f (1)
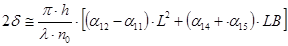 , (2) , (2)
где 2d×-разность фаз на выходе, 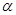 ij
– магнитооптические константы ij
– магнитооптические константы 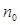 - показатель преломления света в гематите ( - показатель преломления света в гематите (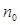 » 2,84 [2]) при L = 0. Поскольку разность фаз (2 » 2,84 [2]) при L = 0. Поскольку разность фаз (2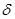 ) равна: 2 ) равна: 2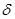 = 2 = 2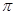 h(n1
–n2
)/ h(n1
–n2
)/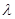 , то зависимость ДП ( , то зависимость ДП (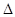 n = n1
–n2
) от величины магнитного поля в базисной плоскости (B
^С
3
) можно представить, исходя из (1) и (2) в виде: n = n1
–n2
) от величины магнитного поля в базисной плоскости (B
^С
3
) можно представить, исходя из (1) и (2) в виде:
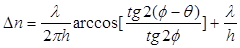 (3), (3),
где слагаемое l./h учитывает дополнительный сдвиг фаз в 2p, возникающий в толстом образце по сравнению с тонким. Экспериментальная зависимость эффекта ДП ( Dn(В)) при фиксированном значении угла f = 22.5о
от величины магнитного поля высокой однородности также представлена на Рис.2 (пуст.треуг.).
 
Рис. 5. Рис. 6.
Там же сплошной линией представлены результаты подгонки экспериментальных данных для ДП света методом наименьших квадратов. Это позволило определить значения констант, входящих в выражение (2) (L= 0,1740 T [3]): a12
- a11
» 1.02×10-2
T-2
, a14
+ a15
» 4.8×10-9
T-2
.
Для напыления нанокомпозитов использовались сплавные мишени Со, Co84
Nb14
Ta2
, Fe41
Co39
B20
и Co45
Fe45
Zr10
размером 270 х 80 мм2
с закрепленными на ее поверхности пластинами из монокристалла кварца, алюмооксида или другого диэлектрика шириной ~ 9 мм, расположенными перпендикулярно продольной оси сплавной мишени. Неравномерное расположение навесок и конструктивные особенности оригинальной установки напыления позволили в одном технологическом цикле получить непрерывное распределение соотношений металлической и диэлектрической фаз композита. Пленки наносились на ситалловую подложку и имели толщину порядка 10 мкм. Измерения комплексной магнитной проницаемости проводились резонансным методом в диапазоне частот 15-150 МГц на образцах прямоугольной формы размером 2×60 мм2
. Высокочастотное магнитное поле было приложено в плоскости пленки вдоль длинной стороны образца. Кривые намагниченности композитов измерялись вибрационным магнитометром при различной геометрии положения образца и внешнего постоянного поля подмагничивания. Измерение удельного электрического сопротивления выполнялось на образцах специальной формы потенциометрическим методом.
На зависимостях действительной (μ/
) и мнимой (μ//
) частей комплексной магнитной проницаемости наногранулированных композитов (Co40
Fe40
B20
)Х
(SiO2
)100-
X
от содержания металлической фазы на частотах 30, 60, 90, 150 МГц можно выделить несколько характерных областей концентрации х, где наблюдается существенное различие в поведении μ/
и μ//
. При концентрации х < 45 ат. % величина комплексной магнитной проницаемости составляет величину несколько единиц и практически не изменяется в широком диапазоне изменения содержания металлической фазы. Изменение кривых намагниченности для этих композитов показывает характерные зависимости, свойственные для суперпарамагнетиков. В этом случае магнитный момент каждой гранулы направлен вдоль оси легкого намагничивания частицы в одном из двух эквивалентных направлений (в случае одноосной магнитной анизотропии) и не коррелирует с намагниченностью соседних гранул. В общем случае скорость разрушения магнитной упорядоченности после снятия магнитного поля зависит от температуры, величины поля анизотропии гранулы и силы дипольного взаимодействия между магнитными частицами в композите.
Так как в исследуемых композитах (Co40
Fe40
B20
)Х
(SiO2
)100-
X
ферромагнитные гранулы состоят из сплава Co40
Fe40
B20
, который имеет аморфную структуру, можно предположить, что поле анизотропии будет иметь меньшую величину по сравнению с кристаллическими частицами из-за отсутствия кристаллографической анизотропии. При этом увеличение концентрации металлической фазы приведет к ферромагнитному упорядочению композита при комнатной температуре несколько раньше, чем электрический порог перколяции.
При концентрациях металлической фазы от 42 до 53 ат. %, на концентрационных зависимостях комплексной магнитной проницаемости как для μ/
, так и μ//
мы наблюдаем хорошо выраженный перегиб. Структура композитов данного диапазона концентрации характеризуется наличием кластеров соприкасающихся ферромагнитных частиц и отдельными изолированными гранулами, магнитное дипольное взаимодействие между которыми приводит к объемному магнитному упорядочению при комнатной температуре. Кривые намагничивания композитов (Co40
Fe40
B20
)Х
(SiO2
)100-
X
при данных концентрациях уже не описываются функцией Ланжевена и характеризуются зависимостями, типичными для ферромагнитных сплавов. Однако значения комплексной магнитной проницаемости для данного диапазона концентраций остаются достаточно низким (<50).
Дальнейшее увеличение концентрации металлической фазы (х > 52 ат. %) приводит к росту комплексной магнитной проницаемости и характеризуется наличием максимума μ(х) в районе х = 55-57 ат. %. Структура композита в этом случае характеризуется наличием бесконечной сетки физически соприкасающихся металлических гранул и между магнитными моментами атомов отдельных частиц устанавливается прямое обменное взаимодействие, а магнитная структура становится аналогичной структуре объемных ферромагнитных материалов. Кривые намагничивания композитов (Co40
Fe40
B20
)Х
(SiO2
)100-
X
при данных концентрациях показывают хорошие магнитомягкие свойства.
Увеличение частоты измерения комплексной магнитной проницаемости от 30 до 150 МГц приводит к уменьшению абсолютной величины μ/
, как в диапазоне концентрации металлической фазы от 42 до 53 ат. % так и при х > 52 ат. %. Мнимая часть комплексной магнитной проницаемости также увеличивается.
Исследования кривых намагничивания композитов (Co40
Fe40
B20
)Х
(SiO2
)100-
X
в плоскости пленки при различной концентрации металлической фазы показали, что при х = 40 ат. % пленка в плоскости образца является изотропной, тогда как при х ≥ 46 ат. % трудная ось намагничивания лежит перпендикулярно оси образца. Поле анизотропии в этих составах композитов порядка 100 Э. Измерение комплексной величины магнитной проницаемости проводилось вдоль легкой оси намагничивания, что уменьшает значения μ/
в высокочастотном диапазоне измерения.
Исследования зависимостей действительной и мнимой частей комплексной магнитной проницаемости композитов (Co40
Fe40
B20
)58,5
(SiO2
)41,5
на частоте 16 МГц от постоянного внешнего магнитного поля, приложенного в различных направлениях образца, показали, что для композита (Co40
Fe40
B20
)47,7
(SiO2
)52,3
поле направленное перпендикулярно оси образца приводит к увеличению значений μ/
в полях до 50 Э в и 200 Э перпендикулярно плоскости пленки. В то же время как для (Co40
Fe40
B20
)58,5
(SiO2
)41,5
и (Co40
Fe40
B20
)58,5
(SiO2
)41,5
поле, приложенное в любом направлении, понижает значение μ/
.
Это свидетельствует о сильной дисперсии локальных полей анизотропии в композите (Co40
Fe40
B20
)Х
(SiO2
)100-
X
. Значение мнимой магнитной проницаемости понижается во всех исследованных образцах при любой ориентации внешнего поля.
Сложный характер температурной зависимости тангенса угла магнитных потерь (tg(φ)) от температуры наблюдается в системах, где происходит смена магнитной фазы. При температуре бифуркации наблюдается минимум tg(φ). При возрастании температуры и переходе системы в суперпаромагнитное состояние потери увеличиваются и большей частоте соответствует большее значение tg(φ). При понижении температуры от магнитного перехода величина потерь проходит через максимум и затем tg(φ), соответствующий большей частоте, спадает быстрее, чем потери при меньших частотах, что может свидетельствовать о релаксационной природе данных потерь. С увеличением концентрации металлической фазы tg(φ) от температуры увеличивается монотонно с ростом Т .
Анализ экспериментальных данных по влиянию термического отжига на высокочастотные магнитные свойства композитов (Co45
Fe45
Zr10
)x
(SiO2
)1-x
показал, что величина комплексной магнитной проницаемости после термообработки у нанокомпозитов, расположенных за порогом протекания, изменяется в разной степени в зависимости от концентрации металлической фазы. Наибольший спад действительной и мнимой частей комплексной магнитной проницаемости наблюдается у композитов, расположенных вблизи порога перколяции, а для композитов от 48 до 53 ат. % наблюдается рост действительной части комплексной магнитной проницаемости. Такое поведение, вероятно, связано с влиянием магнитной анизотропии, индуцированной механическими напряжениями из-за различия температурных коэффициентов линейного расширения композита и подложки, а также анизотропии формы образцов, влияющих на изменение магнитной структуры композитов при термообработке. Поскольку форма образцов для разных композитов одинакова, влияние анизотропии формы на магнитную структуру тоже одинаковое. Магнитная анизотропия, индуцированная механическими напряжениями на границе пленка – подложка зависит от различия температурных коэффициентов линейного расширения, величины магнитострикции аморфного сплава Co45
Fe45
Zr10
, и различна для разных композитов. У гранулированных композитов с матрицей из SiO2
, расположенных вблизи порога перколяции, напряжения, возникающие на границе раздела пленка - подложка меньше, чем у композитов, расположенных за порогом перколяции.
При термомагнитном отжиге помимо анизотропии, индуцированной механическими напряжениями, и анизотропии формы образца на магнитную структуру ферромагнитных композитов оказывает влияние анизотропия, наведенная внешним магнитным полем. Конкуренция всех этих факторов приводит к формированию неоднородной магнитной структуры, зависящей от концентрации магнитной фазы. Для композитов с гранулированной и лабиринтной структурой гранул внешнее магнитное поле, применяемое при термомагнитной обработке, оказывается недостаточным для формирования наведенной магнитной анизотропии и значения m'
и m''
не отличаются от таковых после обычной термической обработки.
Для составов композитов порядка Х ~ 55 ат. % металлической фазы магнитная анизотропия, наведенная магнитным полем, начинает доминировать над магнитоупругой и приводит к росту величин m'
и m''
. Следует отметить, что при формировании «сплошной» магнитной среды с включениями гранул диэлектрической фазы после термомагнитного отжига значения действительной и мнимой части комплексной магнитной проницаемости повышают свои значения по сравнению с простым термическим отжигом.
Изучено влияние внешнего постоянного магнитного поля различной ориентации на поведение m'
и m''
аморфных композитов (Co45
Fe45
Zr10
)x
(SiO2
)1-x
при комнатной температуре. Показано, что при ориентации высокочастотного измерительного и постоянного магнитного поля (Н) в плоскости пленки параллельно продольной оси образца, величины m'
и m''
уменьшаются и в поле насыщения стремятся к единице. При ориентации оси образца перпендикулярно приложенному магнитному полю Н величина комплексной магнитной проницаемости в малых полях возрастает, достигая максимума, а затем уменьшается и в поле насыщения стремится к единице. На основании полученных результатов установлено, что ось легкого намагничивания в ферромагнитных композитах (Co45
Fe45
Zr10
)x
(SiO2
)1-x
имеет преимущественное направление параллельно продольной оси образца.
Добавление реактивных газов в процессе получения композитов приводит к смещению порога перколяции композита в сторону увеличения концентраций металлической фазы и уменьшению значений величины комплексной магнитной проницаемости.
Уменьшение эффекта линейного ДП в малых полях B<BS
, (BS
– поле монодоменизации) связано, как показано в [1,2], с доменной структурой образца. Несмотря на то, что в пределах каждого домена вектор АФ не равен нулю, суммарный вектор в образце L
 0 при В
0 при В  0, и, как следствие, разность фаз 2d
0, и, как следствие, разность фаз 2d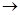 0. То есть эффект линейного магнитного ДП в многодоменных образцах уменьшается при B<BS
и исчезает при B = 0.
0. То есть эффект линейного магнитного ДП в многодоменных образцах уменьшается при B<BS
и исчезает при B = 0.
Во втором случае, когда z-компонента магнитного поля отлична от нуля (Bz
¹ 0), значительный вклад в ДП света вносит недиагональная компонента тензора диэлектрической проницаемости exy
. При Bz
¹ 0 компонента exy
отлична от нуля и в системе координат Х
║В
║C
2
, Y
║L
, Z
║C
3
определяется выражением exy
= a3
ВzL (a3
– соответствующий магнитооптический коэффициент)[1-3]. В этом случае нормальные оптические моды в образце (в рассматриваемой геометрии эксперимента) имеют эллиптическую поляризацию с осями эллипсов вдоль осей Х
и Y
, большие полуоси которых взаимно ортогональны [1]. Здесь следует говорить о ДП эллиптически поляризованных волн и о повороте большой полуоси результирующего эллипса на выходе из образца. Согласно [1] зависимость угла поворота плоскости поляризации q от угла f в этом случае можно описать выражением:
tg2(f - q) = (a + b tg2f)/(c + в tg2f) (4)
Здесь мы не приводим громоздких выражений для величин a, b, c, d, входящих в (4), которые в общем виде получены в [1,3]. Отметим лишь, что эти величины являются сложными функциями компонент exx
, eyy
, exy
тензора диэлектрической проницаемости, полученных с учетом АФ вкладов и магнитного поля. (Заметим, что при exy
= 0 выражение (4) переходит в выражение (1)). В отличие от первого случая (Bz
= 0), зависимость tg[2(f-q)] от tg2f носит нелинейный характер и зависимость угла поворота q от магнитного поля определяется не только разностью фаз 2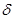 (Вz
≠0)≠2 (Вz
≠0)≠2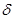 (Вz
=0), но и зависимостью exy
(Bz
), появляющейся в нашем случае вследствие неоднородности поля при большом зазоре магнита. На Рис.3 приведены зависимости tg(2q) от tg(2f) (светл. треуг.–малый зазор, Bz
≈ 0, B = 0,71T, темн. треуг.–большой зазор, Bz
¹0, B=0,71T) полученные из данных, приведенных на Рис.1. Там же сплошными линиями представлены результаты описания этих зависимостей, выражениями (1) и (4) соответственно, методом наименьших квадратов при Bz
= 5,5 mT. (с использованием литературных данных [1,2] и полученных выше значений магнитооптических констант). Таким образом, на основании вышеизложенного можно отметить, что полученное хорошее согласие экспериментальных и расчетных данных является, с одной стороны, еще одним подтверждением теории магнитного ДП света в АФ и, с другой стороны, указывает на возможность проявления аналогичных нелинейных зависимостей в магнитных полях при изучении различных свойств сильных магнетиков с использованием оптических методов регистрации, основанных на явлении линейного и кругового ДП. (Вz
=0), но и зависимостью exy
(Bz
), появляющейся в нашем случае вследствие неоднородности поля при большом зазоре магнита. На Рис.3 приведены зависимости tg(2q) от tg(2f) (светл. треуг.–малый зазор, Bz
≈ 0, B = 0,71T, темн. треуг.–большой зазор, Bz
¹0, B=0,71T) полученные из данных, приведенных на Рис.1. Там же сплошными линиями представлены результаты описания этих зависимостей, выражениями (1) и (4) соответственно, методом наименьших квадратов при Bz
= 5,5 mT. (с использованием литературных данных [1,2] и полученных выше значений магнитооптических констант). Таким образом, на основании вышеизложенного можно отметить, что полученное хорошее согласие экспериментальных и расчетных данных является, с одной стороны, еще одним подтверждением теории магнитного ДП света в АФ и, с другой стороны, указывает на возможность проявления аналогичных нелинейных зависимостей в магнитных полях при изучении различных свойств сильных магнетиков с использованием оптических методов регистрации, основанных на явлении линейного и кругового ДП.
Литература:
[1] В.А. Иванов, Т.Г. Аминов, В.М. Новоторцев, В.Т. Калинников. Известия академии наук. Серия Химическая, 11,
2255 (2004).
[2] В.М. Новоторцев, В.Т. Калинников, Л.И. Королёва. С.Ф. Маренкин. ЖНХ, 50
, 4, 552 (2005).
[3] Р.В. Демин, Л.И. Королева. Актуальные проблемы физики твердого тела. ФТТ-2005, 2,
410 (2005).
[4] Sungyoul Choi, Jeongyong Choi, Soon Cheol Hong and Sunglae Cho, Yunki Kim and John B. Ketterson. Journal of the Korean Phisical Society 42
, S739 (2003).
[5] Н.П. Лякишев, О.А. Банных, Л.Л. Рохлин. Диаграммы состояния двойных металлических систем / Под общ. ред. Н.П. Лякишева. Машиностроение, М. (1997). 1024 с.
[6] А.В. Новосёлова, В.Б. Лазарев. Физико-химические свойства полупроводниковых веществ. Наука, М. (1979). 340 с.
|