Контрольная работа: Кинематический и силовой расчет привода
|
Название: Кинематический и силовой расчет привода Раздел: Промышленность, производство Тип: контрольная работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Министерство образования и науки Российской Федерации Филиал Ухтинского Государственного Технического Университета в г. Усинске Контрольная работа по теории механизмов и машин ТММ 72 00 00 00Р Зачетная книжка № 012300 Зачтено« » ................................................................................. 2004 г Преподаватель Выполнил студент Группы РЭНГМ – 00 14.04.2004г. 1 Задание на контрольную работу № 1 По заданию 2 и варианту 7 для схемы привода изображенной на рисунке 1, решить следующие задачи: - выбрать асинхронный э/двигатель, - вычислить скорость вращения, мощность и крутящий момент для каждого из валов привода, - рассчитать клиноременную передачу, - рассчитать зубчатую тихоходную цилиндрическую передачу, - рассчитать цепную передачу.
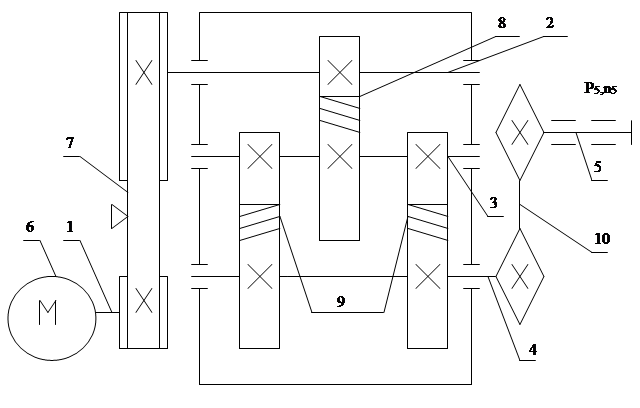
Рисунок 1 -схема привода 1,2,3,4,5, -соответственно валы э.двигателя быстроходный , промежуточный, и тихоходный редуктора и выходной вал привода, 6- э.двигатель ,7- ременная передача , 8 и 9-соответственно быстроходная и тихоходная зубчатая передачи редуктора 10-цепная передача. Мощность Р5 и частота вращения n5 выходного вала привода равны соответственно 18 кВт и 50 об/мин. 1.2.Кинематический и силовой расчет привода.
2.1 Выбор электродвигателя
2.1.1 Требуемая мощность электродвигателя(2, стр.4) Ртр =Р5 /η (2.1) где Р5 - мощность на выходе привода, кВт η – КПД привода η=η(р) · η(з)2 · η(п)4 · η(ц) (2.2) где η(р), η(з), η(п), η(ц) – соответственно КПД ременной, зубчатой цилиндрической, пары подшипников качения и цепной передачи. Руководствуясь рекомендациями (2, стр.5) принимаем η(з) = 0,97, η(ц) = 0,95, η(п) = 0,99, η(р) = 0,96 После подстановки численных значений параметров в формулы (2.2) и ( 2.1) получим: η = 0,96 * 0,972 * 0,994 * 0,95 = 0,87 Ртр = 18/0,87 = 20,69 кВт 2.1.2. С учетом требуемой мощности Ртр = 20,69 кВт рассмотрим возможность выбора асинхронных двигателей серии 4А с номинальными мощностями Рн = 18,5 кВт и Рн = 22 кВт. Для первого перегрузка составляет (20,69 - 18,5) * 100%/20,69 = 10,6% при допустимой перегрузке 5%. Далее его не рассматриваем. Для второго недогрузка не более 5,9%. Для ориентировки в выборе двигателя по частоте вращения оценим передаточное отношение привода i(ср), вычисленное по примерно средним значениям рекомендуемых передаточных отношений отдельных передач. Возьмем (2, стр.7) эти значения для зубчатой конической цилиндрической, ременной и цепной передач соответственно i(ср.з.т) = 3, i(ср.з.б) = 3, i(ср.р) = 3, i(ср.ц) = 3. После перемножения получим в результате: i(ср) = 34 = 81 При таком передаточном отношении привода потребуется двигатель с частотой вращения: n = i(ср) * n5 = 81 * 50 = 4050 об/мин 2.1.3. Окончательно выбираем (3, стр.328) ближайший по частоте вращения асинхронный электродвигатель марки 4А180S2УЗ со следующими параметрами: 1. Номинальная мощность: Рн = 22 кВт 2. Номинальная частота вращения: nн = nс * (1-S/100) = 3000 * (1 – 2,1/100) = 2937 об/мин где скольжение S = 2,1%, синхронная частота вращения nс = 3000 об/мин 3. Отношение пускового момента к номинальному Тп /Тн = 1,4 2.2. Передаточные отношения привода и отдельных его передач Общее передаточное отношение привода при частоте вращения входного вала привода n1 = nн i(общ.) = n1 /n5 = nн /n5 (2.3) где n5 – частота вращения выходного вала привода. Расчет по формуле (2.3) даёт: i(общ.) = 2937/50 = 58,74 примем (2, стр.6) передаточные отношения 1 .Для ременной передачи - i(p) = 3 2.Для зубчатой (быстроходной) цилиндрической передачи - i(з,б) = 3 З.Для зубчатой(тихоходной) цилиндрической передачи - i(з,т) = 3 Тогда на долю цепной передачи остается передаточное отношение i(ц) = i(общ)/(i(p) * i(з.б) * i(з.т)) = 58,74/33 = 2,18 2.3. Частоты вращения, угловые скорости, мощности и моменты на валах привода .
2.3.1. Частоты вращения валов n1 = nн = 2937 об/мин n2 = n1 /i(p) = 2937/3 = 979 об/мин n3 = n2 /i(з.б) = 979/3 = 326.33 об/мин n4 = n3 /i(з.т) = 326.33/3 = 108.8 об/мин n5 = n4 /i(ц) = 108.8/2.18 = 50 об/мин Примечание: здесь и далее параметры, относящиеся к валам привода, обозначены числовыми индексами, соответствующими нумерации валов на схеме привода 2.3.2. Угловые скорости валов ω1 = π * n1 /30 = 3.14 * 2937/30 = 307.4 рад/с ω2 = ω1 /i(p) = 307.4/3 = 102.47 рад/с ω3 = ω2 /i(з.б) =102,47/3 = 34,16 рад/с ω4 = ω3 /i(з.т) = 34,16/3 = 12,56 рад/с ω5 = ω4 /i(ц) = 12,56/2,72 = 4,6 рад/с 2.3.3. Мощности на валах привода Р1 = Ртр = 20,69 КВт Р2 = Р1 * η(р) * η(п) = 20,69 * 0,96 * 0,99 = 19,7 кВт Р3 = Р2 * η(з) * η(п) = 19,7 * 0,97 * 0,99 = 18,9 кВт Р4 = Р3 * η(з) * η(п) = 18,9 * 0,97 * 0,99 = 18,2 кВт Р5 = Р4 * η(ц) * η(п) = 18,2 * 0,95 * 0,99 =17,1 кВт 2.3.4. Моменты на валах привода Т1 = Р1 / ω1 = 20,69 * 103 /307,4 = 67,3 Н * м Т2 = Р2 / ω2 = 19,7 * 103 / 102,47 =192,3 Н * м Т3 = Р3 / ω3 = 18,9 * 103 /34,16 = 553,3 Н * м Т4 = Р4 / ω4 = 18,2 *103 /12,56 = 1449 Н * м Т5 = Р5 / ω5 = 17,1 * 103 /4,6 = 3717 Н * м 2.3.5. Максимальные моменты при перегрузках на валах Т1 max = T1 * 1,4 = 67,3 * 1,4 = 94,22 Н * м Т2 max = Т2 * 1,4 = 192,3 * 1,4 = 269,22 Н * м T3 max = Т3 * 1,4 = 553,3 * 1,4 = 774,62 Н * м T4 max = Т4 * 1,4 = 1449 * 1,4 = 2028,6 Н * м T5 max = Т5 * 1,4 = 3717 * 1,4 = 5203,8 Н * м 2.3.6. Результаты расчетов, выполненных в подразделе2.3. сведены в таблицу 2.1. Частоты вращения, угловые скорости, мощности и моменты на валах привода.
3.Расчет клиноременной передачи. Из раздела 2 заимствуем следующие данные P1 = 20,69 кВт n1 = 2937 об/мин iр = 3 Т1 = 67,3 Н * м В зависимости от частоты вращения малого шкива и передаваемой мощности выбираем по монограмме (2.С.134) клиновой ремень сечения А,с площадью поперечного сечения F=81 мм2 Определяем диаметр меньшего шкива d1 (2.c.l30) d1 >=3*(T1 )1/3 d1 = 3 * (67300)1/3 = 121,86 мм по ГОСТу принимаем d1 = 125 мм Определяем диаметр большего шкива d2 и согласуем с ГОСТ: d2 = ip * d1 * (1 – ε) = 3 * 125 * (1 – 0,015) = 369 мм где ε – коэффициент упругого скольжения по ГОСТу принимаем d2 = 400 мм при этом фактическое передаточное отношение ip = d2 /(d1 * (1 – ε)) = 400/(125 * (1 – 0,015)) = 3,05 Расхождение составляет (3,05 – 3)/3 * 100% = 1,6% что меньше допускаемых обычно 3% Выбираем межосевое расстояние арем арем = 600 мм (это не противоречит условию) (d1 + d2 ) ≤ арем ≤ 2,5(d1 + d2 ) 525 ≤ арем ≤ 1312,5 Определяем длину ремня L: L = 2 * арем + (π/2) * (d1 + d2 ) + (d2 – d1 )2 /(4 * арем ) = = 2 * 600 + (3,14/2) * (125 + 400) + (400 – 125)2 /(4 * 600) = 2056 мм Из (2.стр.121) L = 2000 мм Соответствующее этой длине межосевое расстояние арем = 0,25 * ((L – w) + ((L – w)2 – 2y))1/2 где w = 0,5 * π * (d1 + d2 ) y = (d2 – d1 )2 После подстановки получаем w = 0,5 * 3,14 * (400 + 125) = 824,25 мм y = (400 – 125)2 = 75625 мм арем = 0,25 * ((2000 – 824,25) + ((2000 – 824,25)2 – 2 * 75625))1/2 = 596 мм Найдем угол охвата меньшего шкива (2.стр.130) φ ≈ 180о – ((d2 – d1 )/арем ) * 60о = 180о – ((400 – 125)/596) * 60о = 152о окружное усилие передаваемое одним клиновым ремнем сечения Б (интерполируя) Р0 = 155 + (177 – 155)/5 * 2 = 159,4 Н Допускаемое окружное усилие на один ремень [Р] = Р0 * Сα * СL * Ср Сα = 1 – 0,003 * (180 – φ) = 1 – 0,003 * (180 – 152) = 0,916 (2.стр.135) Коэффициент учитывающий влияние длины ремня СL = 0,3 * L/L0 + 0,7 = [L0 = 1700] = 0,3 * 2000/1700 + 0,7 = 1,05 Ср = 1 [Р] = 159,4 * 0,916 * 1 * 1,05 = 153,3 Н скорость v = 0,5 * ω1 * d1 = 0,5 * 307,4 * 125 * 0,001 = 19,2 м/с окружное усилие Р = Р1 /v = 20690/19,2 = 1077 Н расчётное число ремней Z = P/[Р] = 1077/153.3 = 7.02 = 7 Примем предварительно напряжение от предварительного натяжения σ0 = 1,6 Н/мм Предварительное натяжение каждой ветви ремня вычисляется по формуле (2.стр.136) S0 = σ0 * F = 1,6 * 81 = 130 H Усилие действующее на валы РВХ = 2 * S0 * Z * sin(φ/2) = 2 * 130 * 7 * sin(152o /2) = 1766 H 1. Задание на контрольную работу №2 На основании результатов решения задачи предыдущей контрольной работы расcчитать следующие передачи привода : - расcчитать зубчатую тихоходную цилиндрическую передачу - расcчитать цепную передачу 2. Расчет тихоходной цилиндрической передачи редуктора.
2.1. Материалы зубчатых колес и допускаемые напряжения. 2.1.1. Для зубчатых колес назначаем дешевую углеродистую качественную конструкционную сталь 45 по ГОСТ 1050-80. После улучшения материал колес должен иметь нижеследующие механические свойства, (2,с.34) Шестерня Колесо Твердость НВ 230...260 НВ 200...225 Предел текучести σТ , не менее 440 МПа 400 МПа Предел прочности σb , не менее 750 МПа 690 МПа 2.1.2. Допускаемое контактное напряжение при расчете зубьев и общем случае (2,стр.33) [σн ] = σн lim в * KHL /[SH ] (4.1) где σн lim в – предел контактной выносливости при базовом числе циклов, МПа; КHL – коэффициент долговечности; [SH ] – коэффициент безопасности. Для стальных колёс с НВ 350 (2,стр.27) σн lim в = 2НВ + 70 (4.2) Коэффициент долговечности (2,стр.33) КHL = 1 если взять [SH ] = 1,15 (2.стр.33), то расчет по формулам (4.1), (4.2) дает [σн ]1 = (2НВ + 70) * КHL /[SH ] = (2 * 230 + 70) * 1/1,15 = 461 МПа (4.3) [σн ]2 = (2НВ + 70) * КHL /[SH ] = (2 * 200 + 70) * 1/1,15 = 409 МПа (4.4) В частном случае для косозубых передач допускаемое контактное напряжение при расчете на выносливость (2.стр.85) [σн ] = 0,45 * ([σн ]1 + [σн ]2 ) (4.5) при соблюдении условия [σн ] < 1,23 * [σн ]мин где [σн ]1 и [σн ]2 – соответственно допускаемые контактные напряжения для шестерни и колеса вычисленные по формуле (4.1). Расчёт по формуле (4.5) даёт [σн ] = 0,45 * (461 + 409) = 391,5 МПа [σн ] < 1,23 * [σн ]мин = 409 МПа условие выполняется 2.1.3. Допускаемое контактное напряжение при кратковременных перегрузках для колес зависит от предела текучести σт и вычисляется по формуле [σн ]max = 2,8 * σт (4.6) при σт = 400 МПа (берётся минимальное значение для колеса) [σн ]max = 2,8 * 400 = 1120 МПа 2.1.4. Допускаемые напряжения изгиба при проверочном расчете зубьев на выносливость вычисляются по формуле /3,с.190/ [σF ] = σFlim в * КFL * KFC /[SF ] (4.7) где σFlim в – предел выносливости материала зубьев при нулевом цикле, соответствующего базовому числу циклов; КFL – коэффициент долговечности при расчёте зубьев на изгиб; КFC – коэффициент, учитывающий влияние двухстороннего приложения нагрузки на зубья (в случае реверсивной передачи); [SF ] – допускаемый коэффициент безопасности (запаса прочности). По рекомендациям (2,стр.43-45) берём: для заданных сталей σFlim в 1 = 1,8 * НВ = 1,8 * 230 = 414 МПа σFlim в 2 = 1,8 * НВ = 1,8 * 200 = 360 МПа при одностороннем нагружении зубьев, КFC = 1 (привод не реверсивный) [SF ] = 1,75 КFL = (NFO /NFE )1/ m (4.8) где m – показатель корня; NFO – базовое число циклов; NFE – эквивалентное число циклов. Для колёс с твердостями зубьев до и более НВ 350 коэффициент m равен соответственно 6 и 9. Для всех сталей принимается NFO = 4·106 . Для обоих колес NFE имеет те же численные значения, что и NHE (см.п.2.1.2.). Оба эти значения (для шестерни – 70*107 , для колеса – 21*107 ) больше NFO = 4*106 , поэтому КFL = 1 (3,стр.191,192). Расчёт по формуле (4.7) даёт соответственно для шестерни и колеса [σF ]1 = 414/1,75 = 236,6 МПа [σF ]2 = 360/1,75 = 205,7 МПа 2.1.5. Допускаемое напряжение изгиба при расчете зубьев на кратковременные перегрузки для сталей с твердостью менее НВ 350 [σн ]max = 0,8*σт (4.9) Расчёт по этой формуле (см.п.2.1.1.) даёт для шестерни и колеса соответственно [σF ]max 1 = 0.8*440=352 МПа [σF ]max 2 = 0.8*400=320 МПа 2.2.Расчёт геометрических параметров быстроходной зубчатой передачи. Межосевое расстояние передачи из условия контактной выносливости активных поверхностей зубьев (2,стр.32) аw = Ка *(u+1)*((T4 *Kн b )/( [σн ]2 *u2 *φba ))1/3 (2.10) где Ка - коэффициент, равный 49,5 и 43 для прямозубых и косозубых колес соответственно; u - передаточное число зубчатой пары, u = 3, (передача понижающая); Т4 - момент на колесе /на большем из колес/, T4 = 1449 H*м Кн b - коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, Кн b = 1,25; [σн ] – допускаемое контактное напряжение, [σн ] = 391,05 МПа; φba - коэффициент ширины венца по межосевому расстоянию, φba = 0,5; В итоге расчёт по формуле (2.10) даёт аw = 43*(3+1)*((1449*103 *1,25)/(391,52 * 32 * 0,5))1/3 = 237 мм Межосевое расстояние округляем до стандартного значения (3,стр.30) аw = 224 мм нормальный модуль (2,стр.36) mн = (0,01…0,02)* аw = (0,01…0,02)*224 =3,36 мм Из стандартного ряда модулей (3,стр.30) берем mн = 3,5 мм Назначим угол наклона зубьев β = 40о (2,стр.37). Тогда число зубьев шестерни Z1 = 2* аw *cosβ/((u+1)*mн ) = 2*224*cos40o /(3+1)*3.5 = 24.5 Примем Z1 = 26, тогда число зубьев колеса Z2 = Z1 * i(з) = 26*3 = 78 Уточненное значение cosβ = (Z1 +Z2 )*mн /(2* аw ) = (26+78)*3.5/(2*224) = 0.8125 Отсюда β = arccos(0.8125) = 36o При Z1 = 26 подрезание зубьев исключается, т.к. условие неподрезания (2,стр.38) Zмин = 17*cos2 β<Z1 = 18 соблюдено, что видно из расчёта. Делительные диаметры шестерни и колеса соответственно d1 = (mн *Z1 )/cosβ = 1.25*26/cos36o = 40 мм d2 = (mн *Z2 )/cosβ = 1.25*78/cos36o = 144 мм Диаметры вершин зубьев da 1 = d1 +2mн = 40+2*3.5 = 47 мм da 2 = d2 +2mн = 144+2*3,5 = 151 мм ширина колеса (берем колесо как нераздвоенное) b≤φba *aw = 0.5*224 = 112 мм. Примем b = 110 Принимаем ширину каждого колеса b2 = 55 Шестерни возьмем шире колес на 4 мм b1 = b2 +4 = 55+4 = 59 мм 2.3. Проверочный расчёт прочности зубьев быстроходной передачи.
2.3.1. Расчётное контактное наряжение (2,стр.31) σн =270/ aw *(Т*Кн *(u+1)3 /(b*u2 ))1/2 ≤ [σн ] (2.11) где Кн – коэффициент нагрузки; b – ширина колеса (нераздвоенного); Окружная скорость колес vδ = ω3 *d1 /(2*103 )=34.16*40/2000=0.68 м/с При такой скорости назначаем восьмую степень точности (2,стр.32) Коэффициент нагрузки (2,стр.32) при проверочном расчёте на контактную прочность Кн =Кнα *Кнβ *Кн v (2.12) где Кнα – коэф., учитывающий неравномерность распределения нагрузки между зубьями; Кнβ - коэф., учитывающий неравномерность распределения нагрузки по длине зуба (по ширине венца); Кн v - коэф., учитывающий дополнительные динамические нагрузки. По рекомендации (2,стр.39,40) назначаем: Кнα =1,07 при восьмой степени точности Кнβ =1,06 твердости зубьев менее НВ 350; Кн v =1 v<5м/с и 8 степени точности По формуле (2.12) Кн =Кнα *Кнβ *Кн v = 1,07*1,06*1 = 1,136 Ширину колеса (нераздвоенного) берем в расчёт минимальную, т.е. b=110 мм Момент на колесе Т4 = 1449 Н*м расчёт по формуле (2.11) даёт σн =270/224*(1449*103 *1,136*(3+1)3 /(110*32 ))1/2 =372,4 МПа что меньше допускаемого напряжения [σн ]=391,5 МПа 2.3.2. Расчёт зубьев на контактную прочность по формуле (2.11) при кратковременных перегрузках моментом T4max=2028.6 Н*м дает σн =270/224*(2028,6*103 *1,136*(3+1)3 /(110*32 ))1/2 =1035 МПа что меньше допускаемого[σн ]=1120 МПа 2.3.3.Напряжения изгиба зубьев цилиндрических колес при проверочном расчёте на выносливость вычисляются по формуле (2,стр.46) σF =Ft *KF *YF *Yβ *KFα /(b*mн )<[σF ] (2.13) Ft – окружная сила, Н; KF – коэф. нагрузки; YF – коэф. формы зуба; Yβ – коэф., компенсирующий погрешности, возникающие из-за применения для косых зубьев той же расчётной схемы, что и для прямых; KFα – коэф., учитывающий неравномерность распределения нагрузки между зубьями; b – ширина колеса, находящаяся в зацеплении (минимальная), мм; mн - модуль нормальный, мм. В зацеплении колес (раздвоенного колеса) тихоходной передачи действуют следующие силы(2,стр.158) окружная Ft = T3 *2/d1 =2*553.3*103 /40=27665 H радиальная Fr = Ft *tg α/cos β = 27665*tg20o /cos36o =12447 H осевая Fa = Ft *tg β = 27665*tg36o = 20098 H Коэффициент нагрузки (2,стр.42) KF = KFβ *KFv (2.14) где KFβ – коэф., учитывающий неравномерность распределения нагрузки по длине зубьев; KFv – коэф., учитывающий дополнительные динамические нагрузки (коэф.динамичности). Примем KFβ =1,11 (2,стр.43) с учётом, что твердость колеса менее НВ 350,. Назначим KFv =1,1, учитывая дополнительно, что окружная скорость v = 0,8 м/с, а степень точности принята восьмая. Тогда по формуле (2.14) KF = 1,11*1,1 = 1,23 Без расчётов, руководствуясь только рекомендацией (2,стр.46), возьмем KFα = 0,92 коэффициент Yβ – определим по формуле (2,стр.46) Yβ = 1-β/140 = 1-36о /140 = 0,74 β – вычисленный уже ранее угол наклона зубьев YF – коэф. формы зуба зависит от эквивалентного числа зубьев (2,стр.46), которое составляет для шестерни Zv 1 = Z1 /cos3 β = 26/cos3 36 = 49 для колеса Zv 2 = Z2 /cos3 β = 78/cos3 36 = 145 Для эквивалентных чисел зубьев соответственно шестерни и колеса находим (2,стр.42) YF 1 = 3,7 YF 2 = 3,6 Подстановка подготовленных численных значений в формулу (2.13) дает для шестерни и колеса соответственно σF 1 = 27665*1,23*3,7*0,74*0,92/(224*3,5) = 109 МПа σF 2 = 27665*1,23*3,6*0,74*0,92/(224*3,5) = 106 МПа Это значительно меньше вычисленных допускаемых напряжений [σF ]1 = 236,6 МПа [σF ]2 = 205,7 МПа Напряжения изгиба при кратковременных перегрузках вычисляются также по формуле (2.13), куда вместо окружной силы рассчитанной для длительно передаваемой мощности, следует подставить окружную силу при кратковременных перегрузках Ft max = T3 max /d1 = 774.62*103 /40 =19365 H После подстановки в формулу (2.13) получаем при перегрузках соответственно для шестерни и колеса напряжения изгиба σFmax 1 = 19365*1,23*3,7*0,74*0,92/(224*3,5) = 76 МПа σFmax 2 = 19365*1,23*3,6*0,74*0,92/(224*3,5) = 74 МПа Эти напряжения значительно меньше вычисленных допускаемых напряжений [σF ]max 1 =352 МПа [σF ]max 2 =320 МПа 2.3.5. Геометрические параметры колес тихоходной зубчатой передачи, обоснованные в результате расчётов, сведены в таблицу.
Расчёт цепной передачи. Выбираем для передачи цепь приводную роликовую ПР по ГОСТ 13568-75 Числа зубьев (3,стр.84) Z1 = 31-2*I = 31-2*2.72 = 26 Z2 = Z1 *I = 26*2.72 = 71 Допускаемое среднее давление примем ориентировочно по табл. 5.15 (3,стр.85) [р] = 37 Н/мм2 , чтобы вычислить Кэ по формуле принимаем kд = 1,25; ka = 1; kн = 1; kp = 1.25; kcm = 1.5; kп = 1 получим Кэ = 1,252 *1,5 = 2,33 число рядов m = 1 Следовательно t = 2.8*((T4 *Кэ /(Z1 *[р]*m)1/3 = 2.8*(1449*1000*2.33/(26*46))1/3 = 39.5 мм Ближайшее стандартное значение по таблице 5.12 (3,стр.82) t = 38.1 мм соответственно F = 473 мм2 ; Q = 12700 кгс; q = 5,5 кг/м. По табл. 5.14 (3,стр.84) условие [n4 ]≥n4 выполнено Условное обозначение цепи: Цепь –ПР-19.05-3180 ГОСТ 13568-75 Определим скорость цепи V = z1 *t*n4 /60000=26*38.1*108.8/60000=1.8 м/с Окружное усилие Р = Р4 /V = 18,2*1000/1,8 = 8402 Н Проверяем среднее давление р = Р*Кэ /F = 8402*2,33/473 = 37,83 Уточняем по табл. 5.15 (3,стр.85) при 55 об/мин [р] = 36,4 Н/мм2 (получено интерполированием) умножая согласно примечанию наёденное значение на поправочный множитель Кz = 1+0,01(z1 -17) получим [р] = 36,8*(1+0,01(26-17)) = 40,11 Н/мм2 Таким образом р<[р] , следовательно выбранная цепь по условию надёжности и износостойкости подходит. Выполним геометрический расчет передачи: принимаем межосевое расстояние а = 40*t; at = a/e = 40 Для определения числа звеньев Lt находим предварительно суммарное число зубьев Z = Z1 +Z2 = 26+71 = 97 Поправку ∆ = (Z2 -Z1 )/(2*π) = (71-26)/(2*3.14) = 7.16 По формуле(3,стр.84) Lt = 2*at +0.5*Z+∆2 /at = 2*40+0.5*97+7.162 /40 = 129.8 Уточняем межосевое расстояние по формуле (3,стр.84) а = 0.25*t*[Lt -0.5*Z+((Lt -0.5*Z)2 -8*∆2 )]1/2 = = 0.25*38.1*[129.8-0.5*97+((129.8-0.5*97)2 -8*7.162 )]1/2 = 1016 мм Для обеспечения свободного провисания цепи следует предусмотреть уменьшение а на 0,4%, т.е. на 1016*0,004 = 4 мм Делительный диаметр меньшей звездочки по формуле (3,стр.82) dд 1 = t/(sin180/Z1 ) = 38.1/(sin(180/26)) = 316 мм большей звездочки dд2 = t/(sin180/Z2 ) = 38.1/(sin(180/71)) = 861 мм наружные диаметры по формуле (3,стр.84) De1 = t/(sin180/Z1 )+1.1*d1 = 38.1/(sin(180/26))+1.1*22.23 = 339 мм здесь d1 – диаметр ролика по табл. 5.12 (3,стр.82) d1 = 22,23 De2 = t/(sin180/Z2 )+0,96*t = 38.1/(sin(180/71))+0.96*38.1 = 896 мм силы действующие на цепь окружная Р = 8402 Н центробежная Рv = q*v2 = 5.5*1.82 = 17.82 H от провисания Pf = 9.819*kf*q*a = 9.81*1.5*5.5*1.013 = 82 H здесь kf = 1,5 при расположении цепи под углом 45о расчетная нагрузка на валы Рв = Р+2*Pf = 8402+2*82 = 8566 H проверяем коэф. запаса прочности по формуле (3,стр.86) n = 9.81*Q/(P+Pv+Pf) = 9.81*12700/(8402+17.82+82) = 14.65 что значительно больше нормативного [n] = 10. Следовательно, условие прочности выбранной цепи также удовлетворительно. Список литературы. 1. Задания к расчетным и контрольным работам по теории механизмов и машин Ухта 2003 г. 2. С.А. Чернавский и др. „КУРСОВОЕ ПРОЕКТИРОВАНИЕ ДЕТАЛЕЙ МАШИН" Москва. „ Машиностроение" , 2-е изд. Переработанное и дополненное.1988г. З. С.А. Чернавский и др. „КУРСОВОЕ ПРОЕКТИРОВАНИЕ ДЕТАЛЕЙ МАШИН", Москва. „ Машиностроение "1979г. 4. П.Г. Гузенков. „Детали машин " издание третье . Москва „высшая школа", 1982г. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||