Курсовая работа: Исследование колебаний механической системы с одной степенью свободы
|
Название: Исследование колебаний механической системы с одной степенью свободы Раздел: Промышленность, производство Тип: курсовая работа | |||||||||||
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Кафедра теоретической механики КУРСОВАЯ РАБОТА «Исследование колебаний механической системы с одной степенью свободы» по разделу «Динамика» Кафедра теоретической механики Рецензия На курсовую работу Студента __Кисова Ивана____________ (фамилия, имя, отчество) Группы _121142__________________ Вариант № ___ количество страниц Курсовая работа по содержанию соотве- тствует / не соответствует выданному заданию и выполнена в полном / не в полном объеме. КР может быть допущена к защите с добавлениембаллов рецензента после успешной защиты. Рецензент_______ /_____________ (Ф.И.О.) «____»_____________200 г. ТУЛА 200 Оглавление Аннотация Содержание задания 1. Применение основных теорем динамики механической системы 1.1.Постановка второй основной задачи динамики 1.2.Определение закона движения системы 1.3.Определение реакций внешних и внутренних связей 2. Построение алгоритма вычислений 3. Применение принципа Лагранжа-Даламбера и уравнений Лагранжа второго рода 3.1. Составление дифференциального уравнения движения механизма с помощью принципа Даламбера - Лагранжа 3.2. Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода Анализ результатов Список использованной литературы Аннотация Дана механическая система с одной степенью свободы, представляющая собой совокупность абсолютно твёрдых тел, связанных друг с другом посредством невесомых нерастяжимых нитей, параллельных соответствующим плоскостям. Система снабжена упругой внешней связью с коэффициентом жесткости с. На первое тело системы действует сила сопротивления R=-µ*V и возмущающая гармоническая сила F(t) = F0 * sin(pt). Трением качения и скольжения пренебрегаем. Качение катков происходит без скольжения, проскальзывание нитей на блоках отсутствует. Применяя основные теоремы динамики системы и аналитические методы теоретической механики, определён закон движения первого тела и реакции внешних и внутренних связей. Произведён численный анализ полученного решения с использованием ЭВМ. В данной курсовой работе мы исследовали динамическое поведение механической системы с использованием основных теорем и уравнений теоретической механики. Дифференциальное уравнение движения механической системы получено тремя способами. Во всех случаях коэффициенты тnp ,п,к получились одинаковыми и совпали с компьютерной распечаткой, что говорит об их правильности. В процессе решения дифференциального уравнения данной механической системы были получены законы движения первого груза, его скорость и ускорение в зависимости от времени t. На основании этих зависимостей были определены законы изменения всех остальных характеристик механической системы, в том числе и реакции связей Содержание задания Исследовать движение механизма с одной степенью свободы. Определить реакции внешних и внутренних связей. Массами нитей и упругих элементов пренебречь. Нити считать нерастяжимыми и абсолютно упругими. В качестве координаты, определяющей положение системы, принять перемещение груза 1 -S. К грузу 1 приложена возмущающая сила F(t). Исходные данные: M1, М2,М3 - массы тел механической системы. с - жесткость упругого элемента. г2 - радиус блока 2. R3 , Гз -радиусы ступеней катка 3. i2 - радиус инерции блока 3. µ - коэффициент сопротивления. Fo — амплитуда возмущающей силы m1= 3mm2= mm3= mm4= 2m r2 =r R2 =3rr3 =rr4 =2r i2 =2r Xo=6 см Xo= 0 см/c m= 1кг r= 0.1 м p = 3.14 F 0 = 50 Н F(t)= F 0 sin(pt) c= 4000 Н/м μ=100Н*с/м R= - μV
Часть 1. ПРИМЕНЕНИЕ ОСНОВНЫХ ТЕОРЕМ ДИНАМИКИ МЕХАНИЧЕСКОЙ СИСТЕМЫ 1.1. Постановка второй основной задачи динамики
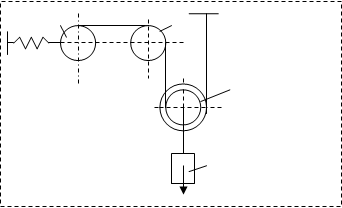
Рис. 1 Расчётная схема На рис. 1 обозначено:
Fупр - упругая реакция пружины,
Fсц - сила сцепления с опорой,
R = - µ*Vсила вязкого сопротивления,
F(t)- возмущающая сила. Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 3 происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 1. Для построения дифференциального уравнения движения системы используем теорему об изменении кинетической энергии механической системы в дифференциальной форме: dT
∑Ne k - сумма мощностей внешних сил, ∑Ni k -сумма мощностей внутренних сил. Теорема (1.1) формулируется так: "Производная по времени от кинетической энергии механической системы равна алгебраической сумме мощностей внешних и внутренних сил, действующих на точки механической системы. Вычислим кинетическую энергию системы как сумму кинетических энергий тел 1-3: T= T1+T2+T3.(1.2) Груз 1 совершает поступательное движение. Его кинетическая энергия равна: T1= 1/2 m1 *υ2 1 (1.3) где Vl - скорость груза 1. Блок 2 совершает вращательное движение около неподвижной оси. Его кинетическая энергия T2 =1/2*m2*υ2 2+1/2*Jc2 ω 2 2 (1.4) где Jn2 = m2 *i2 2 : - момент инерции относительно центральной оси блока; ω2 - угловая скорость блока. Блок 3 совершает вращательное движение, T3 =1/2*Jc3 ω2 3 гдеjc3 =1/2 m3 *r2 3 (1.5) Каток 4 совершает плоскопараллельное движение T =1/2*m4 *vc4 2 +1/2*Jc4 * ω4 2 гдеJc4 = Ѕ*m4 *r4 2 Кинетическая энергия всего механизма будет равна: T=1/2m1 υ1 2 + 1/2m2 *vc2 2 +1/2*Jc2 ω2 2 +1/2*Jc3 ω2 3 + 1/2*m4 *vc4 2 +1/2*Jc4 *ω4 2 (1.6) Выразим υn 3., ω2, ω3 через скорость груза 1 vc 2 = υ1 =υ=S; => ω3 = (R2 + r2 )*v/R3 *V3 vc 4 =ω 4 * r 4 = (R2 + r2 )*v/2R2 (1.7) ω2 =v/r 2 Подставляя (1.3), (1.4), (1.5), в (1.6) с учетом (1.7), и вынося 1/2 и V2 за скобки, получаем:T= 1/2(m +m + Jc2 т пр /R2 2 + Jc3 * (R2 - r 2 ) 2 / R2 * r 2 + m4 (R2 + r 2 ) 2 /4r2 2 + Jc 4 (R2 - r 2 ) 2 /4r2 2 R2 2 )*υ2 T=1/2m тр v3 2 (1-8) т пр =m +m2 +m3 1/R2 2 + 1/2m3 (R2 - r 2 ) 2 / R2 + m4 (R2 + r 2 ) 2 /4r2 2 + m4 (R2 + r 2 ) 2 /4r2 2 т пр =8, 21кг(1-9) Найдем производную от кинетической энергии по времени: dT/dt= т пр – S*S(1.10) вычислим сумму мощностей внешних и внутренних сил. Мощность силы равна скалярному произведению вектора силы на скорость точки ее приложения: N = FV = Fvcos(F, v);(1-11) Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, недеформируемые и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю: ∑N’=0(1.12) Будут равняться нулю и мощности некоторых внешних сил, в том числе сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы N4 , ,Y3 ,X3 ,P3 ,Fвд . Сумма мощностей внешних сил: N=F*V+pV-RV+p2 V2 -Fупр *V4 С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду: (1-13) N= F(t)*V1 +p1 V1 -RV1 + p2 V1 -Fупр V1 * R2 +r2 /2R2 , N =( F(t) +p1 – R +p2 - Fупр R2 +r2 /2R2 )V1 , или N= Fпр * V Где Fnp приведенная сила. Упругую силу считаем пропорциональной удлинению пружины. которое равно сумме статического ѓст и динамического S4 удлинений Fупр =с(ѓст + S4 ) (1-15) Сила вязкого сопротивления R =μ V = μ S тогда Fпр = F(t)+p1 – μ*S+ p 2 – c(ѓст + R2 +r2 /2R2 * S) R2 +r2 /2R2 , (1-16) В состоянии покоя приведенная сила равна нулю. Пологая в (1-16) , что S=’S=0 и F(t)= 0 получаем условие равновесия Fпр = p+ p2 = c *ѓст = R2 +r2 /2R2 =0, (1-17) Отсюда статистическое удлинение пружины равно: - c *ѓст R2 +r2 /2R2 = -p1 - p ; ѓст R2 +r2 /2R2 =(p 1 + p 2 )/c => ѓст =(p 1 + p 2 )/c* 2R2 / R2 +r2 ѓст =1/c (p 1 + p2) * 2R 2 /R2 +r2 ;(1-18) Подставляем выражение (1-18) в, (1-16) получаем окончательное выражение для приведенной силы . ѓпр = F(t) + p1 +p2 - μS – c* R2 +r2 /2R 2 *1/c (p 1 + p2)* *2R 2 /R2 +r2 - c*(R2 + r2 ) 2 /4R2 2 *S ѓпр = F(t) - μS- c*(R2 + r2 ) 2 /4R2 2 *S; (1-19) Подставим выражение для производной от кинетической энергии и сумму мощностей всех сил с учетом (1-19) в (1-1) полуучаем дифференциальное уравнение движения системы ; mпр =S=- c*(R2 + r2 ) 2 /4R2 2 *S- μS+ F0 sin(pt) (1-20) S = 2nS +k2 S +F0 / mпр sin(pt) ; (1-21) Где k циклическая частота свободных колебаний ; n = μ/2* mпр =100/2*8.21= 6.1с -1 ; n – показатель степени затухания колебаний ; k= R2 +r2 /2R2 c/mпр = 1.2 Определение закона движения системы Проинтегрируем дифференциальное уравнение (1.26). Пусть возмущающая сила изменяется по гармоническому закону: F = F0 -S m{pt),(2.1) Где Fo - амплитуда возмущающей силы, р - циклическая частота возмущения. Общее решение S неоднородного дифференциального уравнения (1.26) складывается из общего решения однородного уравнения S и частного решения неоднородного: S=Sод +S . Однородное дифференциальное уравнение, соответствующее данному неоднородному (1.26) имеет вид: S + 2*n*S + kz *S = 0;.(2.2) Составим характеристическое уравнение и найдем его корни L2 +2*n*L + k2! =0, L 1.2 = -n +- n 2 -k 2 ; т.к n <k ,=> решение однородного уравнение имеет вид : Sос =a * e*sin (k 1 *t +β ), где k 1 = k 2 -n 2 ; частное решение дифференциального уравнения ищем в виде правой части: k 1 =18,31с-1 ; Sт= A* sin (pt) + B*cos(pt); далее получаем: (A(k2 - p2 )- 2npB)*sin(pt) + (2 npA +B(k2 - p2 ) )cos(pt)= F0 /mпр *sin(pt); Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева , получаем систему алгебраических уравнений для определения состояния А и В A(k2 - p2 )- 2npB = F0 /mпр решая эту систему получаем следующие выражения 2npА + В(k2 - p2 )= 0 A= k2 - p2 / (k2 - p2 ) 2 + 4n2 p2 * F0 /mпр ; А= 0.011м; B= - 2np/(k2 - p2 ) 2 + 4n2 p2 * F0 /mпр ; B= -0.002м; Общее решение дифференциального уравнения : S= αe–nt sin (k 1 t β) + Asin (pt) + B cos(pt); S= αe–nt (-nsin(k 1 t+β) +k 1 cos(k 1 t+β)) +Apcos(pt) – Bpsin(pt); Постоянные интегрирования αи βопределяем из начальных условий S 0 = α sin(β) + B ; t =0 имеем S 0 = α(- nsin (β) + k 1 cos (β)) + Ap решая эту систему получаем : α= (S 0 - B) 2 + (S 0 - B) - Ap) 2 1/k 2 1 α= 0.045; β= arctg k 1 (S 0 –B) 2 / S 0 +n(S 0 - B)- Ap β=1.2;
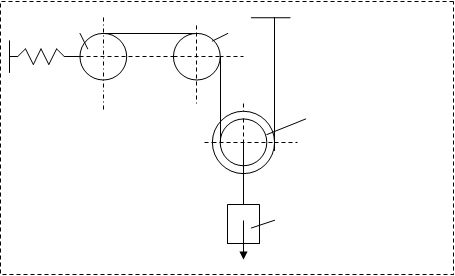
Рис.2 Рис. 2 Для решения этой задачи расчленяем механизм на отдельные части и изображаем расчетные схемы отдельно для каждого тела (рис. 2). Определение реакций связей проведем с помощью теоремы об изменении кинетической момента и теорема об изменения количества движения. Тело№1 αm1 V1 /dt= p1 +T12 S+F+R; наось s : m1 S 1 =p1 +F-R-T12 ; Тело№2 αm2 V2 /dt= p2 +T21 +T20 + T23 ; наось s : m2 S=p2 + T21 -T20 -T23 т.кV2 = V1 =V=S=>dV1 /dt= dV2 /dt;dl2z =∑M2 z dJc2 ω/dt= T20 R- T23 r 2 ; Тело№3 dl 3z /dt=∑M 3z => dJc3 ω 3 /dt= T32 r 3 – T34 r 3 ; Αm3 V3 /dt=x 3 +y3 +p3 +T34 +T12 на ось 0x3 :0=x3 +T34 ; на ось 0y3 : 0=y3 - p3 - T32 ; Тело№4 αm4 V4 /dt=T 43 +P 4 +N 4 +Fcy +F упр ; на ось 0x4 : m 4 S 4 =T 43 -F упр +Fsy с учетом кинематических соотношений (1-7) полученную систему уравнений преобразуем к виду: m 1 S= p 1 +F – R-T 12 ; 0 = N 4 - p 4 ; x 3 = T 34 R m 2 S= p 2 +T 21 - T 20 -T 23 ; y 3 =p 3 +T 34 ‘ J c2 1/R 2 S = T 20 R 2 - T 23 r 2 ; J c4 m 4 R 2 +r 2 /2R 2 r 4 * S=T 43 * J c3 R 2 +r 2 /R 2 r 3 S= T 32 r 3 - T 34 r 3 ; *r 4 - F cy r 4 R m 4 R 2 +r 2 /2R 2 * S= T 43 - Fупр +F cy ; Решая эту систему получаем выражение для определения реакций связей: T 12 = m g + F 0 sin (pt) – μS – mS x2 = T43 T 20 = R 2 r 2 ( p 2 + T 21 - m 2 S) + J c2 S/ R 2 (R 2 +r 2 ); y3 = p2 + T 32 T 23 = R2 2 (p2 + T21 - m2 S) + Jc2 S / R 2 (R 2 +r 2 ); T 43 = T 32 - V c3 /V 3 * (R 2 + r 2 )/ R2 r2 * S F c = T 32 - (R 2 -r 2 )/ R2 r4 *(JC3 r 4 / r 2 r 3 + Jc4 /2r 4 ); Часть 2. ПОСТРОЕНИЕ АЛГОРИТМА ВЫЧИСЛЕНИЙ 2,1 Исходные данные m1 , m2 , m3 , m4 , r 2 , R 2 , r 3 , r 4 , i2 ,μ , F0 , p , S0 , S0 , g ,c. 2,2 Вычисление констант n = μ/2* mпр; k 1 = k 2 - n 2 ; ѓст =1/c (p 1 + p2) * 2R 2 /R2 +r2 ; A= k2 - p2 / (k2 - p2 ) 2 + 4n2 p2 * F0 /mпр ; B= - 2np/(k2 - p2 ) 2 + 4n2 p2 * F0 /mпр ; α= (S 0 - B) 2 + (S 0 - B) - Ap) 2 1/k 2 1 ; β= arctg k 1 (S 0 –B) 2 / S 0 +n(S 0 - B)- Ap ; 2,3 Задание начального времени t=0 2,4 Вычисление значений функций в момент времени t S= αe–nt sin (k 1 t β) + Asin (pt) + B cos(pt); S= αe–nt (-nsin(k 1 t+β) +k 1 cos(k 1 t+β)) +Apcos(pt) – Bpsin(pt); S = 2nS +k2 S +F0 / mпр sin(pt) ; Fупр =с(ѓст + S4 ); 2,5 Вычисление реакций связей T 12 = m g + F 0 sin (pt) – μS – mS x2 = T43 T 20 = R 2 r 2 ( p 2 + T 21 - m 2 S) + J c2 S/ R 2 (R 2 +r 2 ); y3 = p2 + T 32 T 23 = R2 2 (p2 + T21 - m2 S) + Jc2 S / R 2 (R 2 +r 2 ); T 43 = T 32 - V c3 /V 3 * (R 2 + r 2 )/ R2 r2 * S F c = T 32 - (R 2 -r 2 )/ R2 r4 *(JC3 r 4 / r 2 r 3 + Jc4 /2r 4 ); 2,6 Вывод на печать значений искомых функций в момент времени t 2,7 определение значения времени на следующем шаге t = t + ∆t 2.8 Проверка условия окончания цикла t ≤ tкон 2,9 Возврат к пункту 2,4 Часть 3. ПРИМЕНЕНИЕ ПРИНЦИПА ДАЛАМБЕРА-ЛАГРАНЖА И УРАВНЕНИЙ ЛАГРАНЖА ВТОРОГО РОДА 3.1 Составление дифференциального уравнения движения механизма с помощью принципа Даламбера - Лагранжа Общее уравнение динамики системы есть математическое выражение принципа Даламбера - Лагранжа: (1)∑σAk + ∑ σA 0 k =0;
∑ σAk = ∑Fk σrk - сумма элементарных работ всех активных сил на возможном перемещении системы; - сумма элементарных работ всех сил инерции на (=1*■=! возможном перемещении системы.
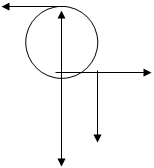
Рис.3 Изобразим на рисунке активные силы и силы инерции (рис 3). Идеальные связи N4 , X3 , Y3 , Fcu не учитывают и не отображают на расчётной схеме, поскольку по определению работа их реакций на любом возможном перемещении равна нулю. Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ: ∑ σA 0 k = Aσ+ σAp + σAp1 +σAp2 + σAp4 + σAF упр ; Вычисляем последовательно элементарные работы активных сил и суммируя их получаем: (2) ∑ σA 0 k = - F пр σS , ∑- σA 0 k = ( - c (R 2 + r2 ) 2 / 4R2 2 * S – μS + F(t)) *σS; Найдем возможную работу сил инерции: ∑ σA 0 k = -φ1 σS1 – φσS2 - M2 σφ2 – M3 σφ3 – φ4 σS4 - M4 φ4 σ ; Запишем выражение для главных векторов и главных моментов сил инерции φ1 = m1 a =m1 S; φ4 = m4 a 4 = m4 S4 ; M 4 = J c4 *E 4 = J c4 * φ4 ; φ2 = m2 a 2 = m2 S 2 ; M 2 = J c2 *E 2 = J c2 * φ2 ; φ3 =0 ; M 3 = Jc 3 *E 3 = Jc 3 * φ3 ; Используя кинематические уравнения (1.7) можно записать σS2 = σ S; σ φ2 = 1/R 2 σ S ; σ φ3 = R 2 + r 2 / R 2 r 3 * σS; σ φ4 = R 2 + r 2 / R 2 r 3 * σS; σS4 = R 2 + r 2 / 2R 2 * σS; S4 = R 2 + r 2 / 2R 2 * S S2 =S ; φ2 = 1/R2 *S; φ3 = R 2 + r 2 / R 2 r 3 * S; φ3 = R 2 + r 2 / 2R 2 r 3 *S; Теперь возможную работу сил инерции можно преобразовать к виду : ∑ σA 0 k = -( m1 +m2 + Jc 2 1/R 2 2 + (R 2 + r 2 )2 / R 2 2 r 3 2 + m4 ( R2 + r 2 )2 / 4R 2 2 + J c4 (R 2 + r 2 )2 / 4R 2 2 r 3 2 )* Sσ S; (3)∑ σA 0 k = - mпр * Sσ S; далее подставляя выражение (2) и (3) в (1) т.е в общее уравнение динамики получаем Поделив это уравнение на σS = 0 получаем дифференциальное уравнение вынужденных колебаний системы: S + 2nS + k2 S = F0 /mпр sin (pt) , где k = R2 +r2 /2R2 c/mпр = 19 , 3 c -1 n = μ / 2 mпр = 6.1 c -1 Полученное нами дифференциальное уравнение полностью совпадает с полученными ранее уравнением 3.2. Составление дифференциального уравнения движения механизма с помощью уравнения Лагранжа 2-го рода Составим теперь уравнение Лагранжа 2-ого рода. В качестве обобщенной координаты примем перемещение груза 1 - S. Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид: d/dt * σ T/ σS - σ T/ σ S (3.3) где Т — кинетическая энергия системы; Q - обобщенная сила; S - обобщенная координата; S - обобщенная скорость. Выражение для кинетической энергии системы было найдено ранее: (3.4) T=1/2m тр v3 2 т пр =m +m2 +m3 1/R2 2 + 1/2m3 (R2 - r 2 ) 2 / R2 + m4 (R2 + r 2 ) 2 /4r2 2 + m4 (R2 + r 2 ) 2 /4r2 2 Производные от кинетической энергии: (3.5) σT/ σS= 0; σT/ σS = т пр S ; d/dt * σT/ σS= т пр S; Для определения обобщенной силы Q сообщим системе возможное перемещение σS (рис.3) и вычислим сумму элементарных работ всех активных сил на возможных перемещениях точек их приложения [см.(2)]. (3.6) ∑ σA 0 k = - F пр σS , ∑- σA 0 k = ( - c (R 2 + r2 ) 2 / 4R2 2 * S – μS + F(t)) *σS; С другой стороны для системы с одной степенью свободы: ∑ σA 0 k =QσS( 3.7) Сравнивая два последних соотношения, получаем: Q = - c (R2 + r 2 ) 2 /4R2 2 *S – μ*S + F(t). Подставляя производные (3.5) и обобщенную силу (3.8) в уравнение Лагранжа(3.3), получаем; Q = - c (R2 + r 2 ) 2 /4R2 2 *S – μ*S + F0 m(pt) , S + 2nS + k2 S = F0 /mпр sin (pt) , где k = R2 +r2 /2R2 c/mпр = 19 , 3 c -1 n = μ / 2 mпр = 6.1 c -1 Анализ результатов В данной курсовой работе мы исследовали динамическое поведение механической системы с использованием основных теорем и уравнений теоретической механики. Дифференциальное уравнение движения механической системы получено тремя способами. Во всех случаях коэффициенты тнр ,п,к получились одинаковыми и совпали с компьютерной распечаткой, что говорит об их правильности. В процессе решения дифференциального уравнения данной механической системы были получены законы движения первого груза, его скорость и ускорение в зависимости от времени t На основании этих зависимостей были определены законы изменения всех остальных характеристик механической системы, в том числе и реакции связей. Использованная литература 1. Методические указания к курсовой работе по разделу "Динамика", "Исследование колебаний механической системы с одной степенью свободы". Разработали: профессор Нечаев Л.М., доцент Усманов М.А. Тула 1998. 2. Яблонский А.А. "Курс теоретической механики." Том 2 - М.: Высшая школа 1984-424 с. 3. Тарг СМ. "Краткий курс теоретической механики" — М.: Наука, 1988 — 482 с.22 |
|||||||||||