МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФГОУ ВПО «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ ИМЕНИ К.Д. ГЛИНКИ»
Кафедра ИОМАС
КУРСОВОЙ ПРОЕКТ ПО МОДЕЛИРОВАНИЮ
на тему:
«Разработка экономико-математической модели по оптимизации отраслевой структуры производства в СХА "Горизонт»
Выполнила:студентка экономического
факультета заочного отделения
2-ое высшее Полякова Э.Ю.
Шифр по зачетке: 09221
Руководитель: д.э.н., зав.кафедрой
Улезько А.В.
Воронеж
2010
Содержание
Введение Стр.3
1. Теоретические и методические основы моделирования экономических процессов в сельскохозяйственном производстве Стр.5
2. Разработка экономико-математической модели по оптимизации отраслевой структуры производства в СХА «Горизонт» Стр.14
2.1. Постановка задачи Стр.14
2.2. Подготовка входной информации Стр.15
2.3. Запись экономико-математической модели в математическом видеСтр.24
2.4. Запись экономико-математической модели в структурном виде Стр.29
2.5. Запись экономико-математической модели в матричном виде Стр.31
3. Анализ результатов решения экономико-математической задачи по оптимизации отраслевой структуры производства в СХА «Горизонт» Стр.32
Выводы и предложения Стр.33
Список используемой литературы Стр.34
Приложения Стр. 36
Введение
Обоснование параметров потенциально эффективного предприятия предполагает формирование такого его сбалансированного ресурсного потенциала, который обеспечивал бы максимальную отдачу каждого производственного ресурса. Под параметрами предприятия в данном случае понимается совокупность показателей, характеризующих величину и структуру материальных ресурсов, количественные и стоимостные результаты деятельности, получаемые при использования ресурсного потенциала. Решение этого вопроса позволяет создать материальную основу производственной системы, на основании которой можно обосновывать способы и методы построения адекватной системы производственных отношений.
Изучение внутренней сущности сельскохозяйственного предприятия, элементов его производственной системы и системы хозяйственного механизма позволяет определить следующие основные направления адаптации аграрного формирования к изменяющимся условиям хозяйствования:
- изменение масштабов производства, позволяющее соблюдать оптимальность ресурсных пропорций;
- корректировка производственного направления за счет отдания приоритета наименее капиталоемким, но эффективным отраслям;
- внедрение гибких технологий, обеспечивающих достаточную свободу маневра всеми видами имеющихся ресурсов и др.
Одним из инструментов принятия стратегического решения об определении перспективных направлений развития предприятия является использование методов математического моделирования, в частности разработка и реализация модели по оптимизации отраслевой структуры производства.
Цель данной работы заключается в том, чтобы исходя из природно-климатических и макроэкономических условий хозяйствования, ресурсного потенциала предприятия определить такую специализацию производства и сочетание отраслей, которые позволили бы достичь максимального экономического эффекта.
Для достижения данной цели были решены следующие задачи:
· изучены теоретические и методические основы оптимизации перспективных параметров сельскохозяйственных предприятий;
· поставлена экономико-математическая задача по оптимизации отраслевой структуры производства и выбран критерий оптимальности;
· подготовлена и обоснована входная информация для экономико-математической модели;
· разработана экономико-математической модели по оптимизации отраслевой структуры производства;
· поставленная экономико-математическая задача реализована на ПЭВМ в многовариантной постановке;
· проведен анализ результатов решения.
В качестве основного метода исследований использовался метод экономико-математического моделирования.
Расчеты проводились с помощью табличного процессора Excel, для реализации задачи линейного программирования использовался пакет оптимизации Solver.
В качестве объекта исследования выбрано сельскохозяйственное предприятие «Горизонт».
1.Теоритические и методические основы моделирования экономических процессов в сельскохозяйственном производстве
Экономико-математические методы представляют собой совокупность математических методов (математического программирования, теории вероятностей, теории массового обслуживания, теории игр, сетевых методов, математической статистики и др.), применяемых при решении разных экономических задач в науке и практике. Однако получение какого-либо количественного результата еще не дает оснований для его немедленного использования в практике планирования и управления народным хозяйством. Необходимо понять качественную природу этого результата. Если этого не учитывать, то полученные решения, будучи идеальными с математической точки зрения, могут оказаться совершенно неприемлемыми с экономической. Если такие понятия, как "математический экстремум" и "экономический оптимум", не совпадают, то результаты экономико-математических расчетов будут условными, абстрактными и, следовательно, практически неприемлемыми. Таким образом, при использовании экономико-математических методов экономической теории принадлежит основная роль, а математике, математическому аппарату - служебная, вспомогательная.
Разработкой и внедрением экономико-математических методов в практику планирования и управления сельским хозяйством занимаются многие научно-исследовательские учреждения и сельскохозяйственные вузы России.
В сельском хозяйстве экономико-математические методы используются по трем основным направлениям:
разработка и решение экономико-математических задач внутрихозяйственного анализа и планирования;
разработка и решение экономико-математических задач на уровне агропромышленных объединений и отдельных звеньев агропромышленного комплекса;
разработка и решение экономико-математических задач отраслевого анализа и планирования.
Разработаны и успешно решаются задачи первого направления, поскольку необходимая для их разработки информация более доступна и достоверна. Решение этих задач на ЭВМ не представляет больших трудностей и не требует усилия больших коллективов. К задачам первого направления относятся следующие задачи оптимизации: использование кормов на фермах и в хозяйствах; использование минеральных и органических удобрений; состав и использование машинно-тракторного парка; транспортные перевозки внутри хозяйства; планы развития животноводства; планы развития растениеводства; производственная структура сельскохозяйственного предприятия; внутрихозяйственное размещение и специализация производства по отделениям, фермам, бригадам и другим подразделениям; планы организационно-хозяйственного устройства сельскохозяйственных предприятий.
Задачи второго направления использования экономико-математических методов, возникшего в связи с организацией агропромышленных объединений, включают задачи оптимизации не только производства продукции сельского хозяйства, но и ее промышленной переработки внутри объединения.
Третье направление использования экономико-математических методов связано с разработкой и решением задач развития отдельных отраслей сельского хозяйства и агропромышленного комплекса в целом на уровне области, края, республики и страны. Задачи этого направления могут быть разработаны и решены только с участием больших коллективов, иногда даже несколько научно-исследовательских институтов.
Основная задача работ этого направления - оптимальное размещение и специализация сельскохозяйственного производства по регионам. Результаты решения подобных задач по отдельным крупным регионам страны показали их высокую эффективность. К этому же направлению относится задача оптимизации закупок сельскохозяйственных продуктов по хозяйствам, районам областям и республикам. Необходимо разрабатывать задачи оптимального развития агропромышленных объединений областного и республиканского уровней. Успешное решение подобных задач будет способствовать повышению эффективности работы агропромышленного комплекса страны.
Основной метод исследования - метод моделирования экономических процессов в сельском хозяйстве, который и определяет комплекс различных приемов, получивших широкое распространение в науке и практике в последние годы.
Под моделированием понимают процесс построения моделей, с помощью которых изучают функционирование (поведение) объектов различной природы.
В самом общем смысле модель - это условный образ, схема объекта исследования. Понятие "модели" связано с наличием сходства между двумя объектами, один из которых может рассматриваться как оригинал, а другой - как его модель. Степень соответствия модели объекту моделирования может быть различной. Модель является важным инструментом научной абстракции, позволяющим выделить в процессе исследования наиболее существенные характеристики изучаемого объекта. В некоторых случаях модель может быть внешне схожа с моделируемым объектом, но отличается от него какими-либо параметрами (размерами, скоростью передвижения и т.д.). Такие модели принято называть физическими (модель самолета, корабля, гидроэлектростанции, планетарий и т.д.). Физическое моделирование успешно используется в науке и технике. Однако физическое моделирование может быть использовано не во всех случаях. Если необходимо изучить объекты или системы достаточно большой сложности, физическая модель заменяется абстрактной, математической, в которой описываются количественные характеристики системы. Математические модели используются в самых различных областях человеческого знания.
Математическое моделирование универсальный и эффективный инструмент познания внутренних закономерностей, присущих явлениям и процессам. Математическое моделирование позволяет изучить количественные взаимосвязи и взаимозависимости моделируемой системы и совершенствовать ее дальнейшее развитие и функционирование. Но для того, чтобы моделирование стало действенным инструментом познания, необходимо правильно построить математическую модель, адекватную изучаемой системе. Математическая модель представляет собой систему математических формул, неравенств или уравнений, с большей или меньшей точностью описывающих явления и процессы, происходящие в оригинале.
Поскольку одни и те же символы и обозначения позволяют описать самые различные процессы, математическая модель широко применяется в науке и практике. Кроме того, она позволяет абстрактно (в общем виде) представить или описать большое количество сложных процессов и явлений. Экономические процессы и явления исследуются с помощью экономико-математических моделей, введенных в практику экономических исследований в нашей стране академиком В.С. Немчиновым.
Сущность экономико-математической модели в сжатой и емкой форме выразил В.С. Немчинов: "Экономико-экономическая модель представляет собой концентрированное выражение общих взаимосвязей и закономерностей экономического явления в математической форме"[1]
.
Среди различных систем наиболее сложными являются экономические, правильно описать которые можно лишь в том случае, если достаточно подробно, хорошо познаны количественные связи между отдельными факторами и степень их влияния друг на друга и на конечные результаты производств. Поэтому модель должна с большей или меньшей точностью отражать реальные процессы и взаимосвязи экономической системы и ограничения, накладываемые на нее внешними условиями. Модель должна опираться на достоверную информацию. Однако не одна, даже сложная и большая модель не может до мельчайших подробностей отразить все стороны моделируемой системы. Да в этом и нет особой надобности. Поэтому в процессе построения модели не следует стремиться к описанию многочисленных связей, присущих моделируемой системе, поскольку не всегда точно известно количественная природа всех связей и зависимостей исследуемой системы; кроме того, это может так усложнить и перегрузить модель, что решения с ее помощью конкретной экономической задачи окажется невозможной. Поэтому математическое моделирование предполагает абстрагирование, отвлечение от несущественных сторон моделируемого объекта и, следовательно, описание наиболее характерных закономерных черт его. Однако и абстрагирование имеет свои пределы, за которыми модель становится слишком условной, что не позволяет получить практически приемлемое решение. Следовательно, в процессе моделирования необходимо определить пределы абстрагирования. При этом надо помнить, что любая экономико-математическая модель представляет собой диалектическое единство количественной и качественной характеристик экономического явления. Отсутствие такого единства или нарушение его в модели может привести к нежелательным, а следовательно, и к практически непригодным решениям.
Таким образом, искусство моделирования состоит в том, чтобы, глубоко изучив и поняв качественную природу явления, суметь отразить ее в математической количественной форме, сохранив основные черты явления и отбросив несущественное.
Для изучения экономических процессов, происходящих в народном хозяйстве страны используются и другие методы, например метод научных экспериментов. Однако, как показывает опыт, дешевле и быстрее разработка экономико-математической модели. Решение ее на ЭВМ не зависит от конкретных условий хозяйства, его территориальной удаленности, времени года и других внешних факторов, и решение возможно до тех пор, пока не будут получены объективные, обоснованные практические результаты. Следует отметить, что возможно применение уже готовых типовых (базовых) моделей, экспериментально проверенных и дающих высокий эффект. Такими моделями, как правило, являются модели линейного программирования. Когда поставленная экономическая проблема не может быть решена с помощью ни одной из известных моделей, создается оригинальная модель, которая в дальнейшем проходит все необходимые стадии, вплоть до практической апробации, и только после этого рекомендуется в производство[2]
.
Процесс экономико-математического моделирования можно условно разделить на ряд отдельных, но взаимосвязанных этапов:
постановка задачи и обоснование критерия оптимальности;
разработка структурной математической модели;
сбор и обработка исходной информации;
построение развернутой матрицы задачи (числовой модели);
решение задачи на ЭВМ, анализ и корректировка его.
Рассмотрим более подробно сущность каждого из этих этапов.
Постановка задачи и обоснование критерия оптимальности. На этом этапе требуется, прежде всего, четкая формулировка задач, раскрывающая известные и не известные параметры и цель задачи. Постановка задачи должна свидетельствовать о хорошем знании объекта моделирования.
Критерий оптимальности должен, как правило, соответствовать основной цели экономической системы. Однако путем формулировки одного критерия оптимальности это не всегда возможно. Поэтому в задачу вводят дополнительные ограничения или решают ее последовательно на несколько критериев оптимальности, а затем с помощью сравнительного анализа полученных вариантов решений выбирают тот, который наилучшим образом отвечает поставленным целям.
Как отмечалось, правильная постановка задачи невозможна без предварительного глубокого количественного и качественного анализа моделируемой системы. Такой анализ позволяет точнее выявить условия, в которых функционирует система, и определить степень влияния одного или нескольких существенных факторов на экономические результаты. Анализировать экономические явления и процессы не просто, а в данном случае ставится задача довести до численных характеристик анализируемые явления и процессы. Только при соблюдении этих условий возможно правильно поставить задачу и получить практические результаты.
Разработка структурной математической модели. На этом этапе выбирается базовая модель и в соответствии с поставкой задачи с использованием определенных символов и обозначений записывается математическая модель. В линейном программировании разработаны две базовые модели - модель общей задачи линейного программирования, называемая моделью симплексного метода, и модель транспортной задачи, или модель распределительного метода. На основе этих базовых моделей в зависимости от конкретной постановки задачи записывается математическая модель. Отражающая структуру будущей задачи, ее композицию - структурная модель. Структурная модель позволяет в ёмкой и сжатой форме отразить характер поставленной задачи и условия, включенные в нее. При разработке структурной модели целесообразно использовать унифицированные символику и порядок описания модели.
Сбор и обработка исходной информации. Процесс сбора и обработки исходной информации более сложный и трудоемкий. На этом этапе определяются характер и объем необходимой информации, источники ее получения и способы обработки.
В значительной степени получаемый результат зависит от качества исходной информации. Если даже одна - две цифры, включенные в задачу, будут неверными, то весь результат решения окажется неприемлемым.
При разработке экономико-математических задач самая трудоемкая работа - расчет технико-экономических коэффициентов затрат и выхода продукции. Если на решение задачи на ЭВМ затрачивается 20-30 мин, то на разработку информации - один - два месяца напряженной работы.
Построение числовой матрицы задачи (числовой модели). Матрица представляет собой запись в табличной форме, в которой условия задачи отражены в виде линейных соотношений. Матрица состоит из столбцов и строк. По столбцам матрицы располагаются, как правило, переменные величины, т.е. искомые значения отраслей сельскохозяйственного производства, по строкам - условия задачи, которые называются ограничениями. Технико-экономические коэффициенты матрицы могут означать либо норму затрат, либо норму выхода продукции в расчете на единицу измерения переменной величины. Но каждая матрица содержит особый столбец, в котором отражаются тип и объем ограничений, и особую строку, в которой располагается целевая функция задачи.
Таким образом, развернутая матрица представляет собой задачу, подготовленную к решению на ЭВМ. Обычно матрица строится в соответствии с принятой на вычислительном центре программой расчета. Матрица этой задачи имеет следующий вид:
| Ограничения |
Единица измерения |
Овес |
Ячмень |
Тип и объем ограничений |
1. По использованию пашни
2. По использованию трудовых ресурсов
|
га
чел. - дней
|
1
6
|
1
8
|
< 300
< 2000
|
| Целевая функция - валовая продукция |
руб. |
200 |
250 |
max |
В таком виде матрица передается для решения на ЭВМ в вычислительный центр.
Анализ и корректировка полученного на ЭВМ решения. Анализ решения проводит постановщик задачи, который должен овладеть определенными навыками и приемами анализа.
Анализ должен определить реальность полученного решения, возможность практического использования этого решения в хозяйстве, необходимость корректировки решения и направление корректировки. Корректировка решения может быть проведена с использованием коэффициентов последней симплексной таблицы. Однако если первоначальные параметры задачи изменяются, необходимо повторное решение ее на ЭВМ. Процесс продолжается до тех пор, пока не будет получено практически приемлемое решение[3]
.
2. Разработка экономико-математической модели по оптимизации отраслевой структуры производства в СХА «Горизонт»
2.1. Постановка задачи
За сельскохозяйственной артелью «Горизонт» закреплено 4460 га сельскохозяйственных угодий, в том числе 3195 га пашни, 755 га сенокосов и 510 га пастбищ. В хозяйстве возделывается большинство сельскохозяйственных культур, характерных для центрально-черноземной зоны. Животноводство представлено молочным скотоводством. Фактическое поголовье фуражных коров составляет 500 голов со шлейфом, соответствующим организации стада с замкнутым циклом воспроизводства.
Хозяйство заключило договора на реализацию сельскохозяйственной продукции в следующих объемах: пшеницы - 21300 ц, ячменя - 8520 ц, овса - 2130 ц, гороха - 2663 ц, гречихи - 639 ц, сахарной свеклы - 109000 ц, подсолнечника - 3941 ц., молока - 11900 ц., мяса КРС в живом весе - 1620 ц.
При оптимизации отраслевой структуры производства необходимо найти такое сочетание отраслей, которое обеспечило бы максимально возможную эффективность производства при условии соблюдения всех агротехнических и зооветеринарных требований, выполнении договорных обязательств по реализации продукции, гарантированного обеспечения отраслей животноводства кормами собственного производства.
Поскольку основной целью любой коммерческой организации является получение максимально возможной суммы прибыли, то в данной задаче критерием оптимальности будет являться максимизация суммы чистого дохода, определяемого как разность между стоимостью товарной продукции и общей суммой производственных затрат по предприятию.
2.2. Подготовка входной информации
Для разработки экономико-математической модели данной задачи необходимо подготовить следующую информацию:
· размер площади пашни, пастбищ и сенокосов;
· перечень сельскохозяйственных культур, возделываемых в данном предприятии;
· планируемый уровень урожайности сельскохозяйственных культур, нормы высева семян;
· виды сельскохозяйственных животных, их поголовье, продуктивность, нормы и рационы кормления;
· питательность кормов;
· материально-денежные затраты и затраты труда в расчете на 1 га посева или одну структурную голову сельскохозяйственных животных;
· объемы реализации продукции по договорам;
· цены реализации товарной продукции;
· агротехнические требования и возможные пределы насыщения севооборотов отдельными сельскохозяйственными культурами.
При подготовке входной информации необходимо обосновать уровень урожайности сельскохозяйственных культур, на основе расчета технологических карт определить нормативный уровень производственных затрат и затрат труда по каждой сельскохозяйственной культуре. Информация о планируемых уровнях урожайности сельскохозяйственных культур, затратах материально-денежных средств и труда в расчете на 1 га приведены в таблице 1.
Таблица 1. Планируемый уровень урожайности сельскохозяйственных культур, производственные затраты и труда на 1 га посева
| Сельскохозяйственные культуры |
Планируемая урожайность, ц/га |
Материально-денежные затраты на 1 га, тыс.руб. |
Затраты труда на 1 га, чел-дней |
| Озимая пшеница |
40 |
3,4 |
1,8 |
| Ячмень |
23 |
2,9 |
1,4 |
| Овес |
26 |
2,7 |
1,4 |
| Горох |
18 |
2,9 |
1,6 |
| Гречиха |
16 |
2,3 |
1,2 |
| Сахарная свекла |
228 |
16,5 |
4,5 |
| Подсолнечник |
13 |
3,3 |
1,5 |
| Кормовая свекла |
393 |
13,5 |
4,1 |
| Кукуруза на силос |
229 |
4,0 |
2,6 |
| Кукуруза на зеленый корм |
210 |
3,9 |
2,4 |
| Однолетние травы на сено |
37 |
1,9 |
1,1 |
| Однолетние травы на зеленый корм |
119 |
2,2 |
1,2 |
| Многолетние травы на сено |
25 |
1,7 |
1,0 |
| Многолетние травы на зеленый корм |
214 |
1,9 |
1,2 |
| Озимые на зеленый корм |
106 |
2,1 |
1,2 |
| Пар |
1,5 |
0,8 |
| Сенокосы |
25 |
1,1 |
0,7 |
| Пастбища |
33 |
0,3 |
0,1 |
Продуктивность крупного рогатого скота принята на следующем уровне: среднегодовой надой на 1 фуражную корову составляет 28 ц.; прирост в расчете на 1 структурную голову принят на уровне 3,16 ц, а реализация прироста – 3,41 ц. Затраты труда на 1 структурную голову составляют 19,3 чел.-дня, а материально-денежные затраты (без стоимости кормов) – 18,3 тыс. руб.
При подготовке входной информации для данной модели необходимо провести распределение основной и побочной продукции, получаемой с 1 га посева сельскохозяйственных культур на различные цели: на семена, реализацию, на корм скоту и т.д. (табл. 2.)
Таблица 2.Распределение продукции сельскохозяйственных культур, полученной с 1га посева, ц
Сельскохозяйственные культуры
|
Выход продукции
с 1 га, ц
|
Отходы, ц |
Семена со страховым фондом, ц |
На корм скоту |
Товарная продукция |
| основной |
побочный |
основной |
побочный |
в натуральном выражении, ц |
в денежном выражении, тыс. руб. |
| Озимая пшеница товарная |
40 |
60 |
1,2 |
2,5 |
1,2 |
60 |
36,3 |
9,075 |
| Озимая пшеница фуражная |
40 |
60 |
1,2 |
2,5 |
37,5 |
60 |
| Ячмень товарный |
23 |
23 |
0,69 |
3,3 |
0,69 |
23 |
19,01 |
4,182 |
| Ячмень фуражный |
23 |
23 |
0,69 |
3,3 |
19,7 |
23 |
| Овес товарный |
26 |
26 |
0,78 |
2,42 |
0,78 |
26 |
22,8 |
4,104 |
| Овес фуражный |
26 |
26 |
0,78 |
2,42 |
23,58 |
26 |
| Горох товарный |
18 |
14,4 |
0,54 |
3,52 |
0,54 |
14,4 |
13,94 |
4,461 |
| Горох фуражный |
18 |
14,4 |
0,54 |
3,52 |
14,48 |
14,4 |
| Гречиха |
16 |
0,48 |
1,1 |
14,90 |
14,42 |
6,056 |
| Сахарная свекла |
228 |
91,2 |
91,2 |
228 |
22,8 |
| Подсолнечник |
13 |
0,39 |
12,61 |
7,062 |
| Кормовая свекла |
393 |
393 |
| Кукуруза на силос |
229 |
45,8 |
183,2 |
| Кукуруза на зеленый корм |
210 |
210 |
| Однолетние травы на сено |
37 |
37 |
| Однолетние травы на зеленый корм |
119 |
119 |
| Многолетние травы на сено |
25 |
25 |
| Многолетние травы на зеленый корм |
214 |
214 |
| Озимые на зеленый корм |
106 |
106 |
| Сенокосы |
25 |
25 |
| Пастбища |
33 |
33 |
При распределении продукции следует учесть следующие моменты:
· по группе зерновых культур и подсолнечнику нормативный процент отходов по товарным культурам составляет 3%; данные отходы (за исключением гречихи и подсолнечника) направляются на корм скоту;
· нормативный процент угара силосной массы составляет 20% от урожайности кукурузы, возделываемой на силос;
· планируется производство собственных семян по группе зерновых культур;
· предусматриваются следующие коэффициенты выхода побочной продукции (от основной): по озимой пшенице - 1,5, по ячменю и овсу - 1, по гороху - 0,8, по сахарной свекле (ботва) - 0,4.
В таблице 3 проведен расчет потребности в семенах собственного производства в расчете на 1 га посева.
Таблица 3. Расчет потребности в семенах собственного производства на 1 га посева
| Сельскохозяйственные культуры |
Норма высева на 1 га, ц |
Страховой фонд,% |
Всего со страховым фондом, ц |
| Озимая пшеница |
2,5 |
0% |
2,50 |
| Ячмень |
3,0 |
10% |
3,30 |
| Овес |
2,2 |
10% |
2,42 |
| Горох |
3,2 |
10% |
3,52 |
| Гречиха |
1,0 |
10% |
1,10 |
Выход корма по зерновым фуражным культурам определяется как разница между производством основной продукции (графа 1) и потребностью в семенах со страховым фондом (графа 4). По зерновым товарным культурам на корм направляются зерноотходы (графа 3). По остальным культурам (за исключением подсолнечника и сахарной свеклы) на корм используется 100 % валового сбора основной продукции (графа 1). Выход корма по кукурузе на силос определяется с учетом нормативного угара силоса. Побочная продукция (графа 2) используется на корм полностью.
Объем товарной продукции в натуральном выражении определяется как разница между выходом основной продукции с 1 га (графа 1), нормативным количеством отходов (графа 3) и потребностью в семенах со страховым фондом (графа 4). Товарная продукция в денежном выражении определяется путем умножения товарной продукции в натуральном выражении на цены реализации.
Планируется следующий уровень цен реализации (руб. за 1 ц.): пшеницы - 250, ячменя - 220, овса - 180, гороха - 320, гречихи - 420, сахарной свеклы - 100, подсолнечника -560, молока - 650, прироста КРС - 3500.
Важным элементом рациональной структуры посевных площадей является организация зеленого конвейера, позволяющего обеспечить регулярное поступление зеленой массы в течение всего пастбищного периода. В таблицах 4-5 приведен вариант организации зеленого конвейера, предлагаемого для данного предприятия.
Таблица 4. Распределение зеленой массы кормовых культур по срокам использования, % от выхода с 1 га
| Источники зеленого корма |
Сроки использования зеленых кормов |
| 2-я пол. мая |
1-я пол.
июня
|
2-я пол. июня |
июль |
август |
сентябрь |
| Ботва сахарной свеклы |
100% |
| Кукуруза 1 срока сева |
100% |
| Кукуруза 2 срока сева |
100% |
| Многолетние травы |
60% |
40% |
| Однолетние травы 1 срока сева |
100% |
| Однолетние травы 2 срока сева |
100% |
| Озимые на зеленый корм |
100% |
| Пастбища |
12% |
15% |
17% |
23% |
18% |
15% |
Таблица 5. Распределение зеленой массы кормовых культур по срокам использования, ц
| Источники зеленого корма |
Выход с 1 га, ц. к. ед. |
Сроки использования зеленых кормов |
| 2-я пол. мая |
1-я пол.
июня
|
2-я пол. июня |
июль |
август |
сентябрь |
| Ботва сахарной свеклы |
14,6 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
14,6 |
| Кукуруза 1 срока сева |
44,1 |
0,0 |
0,0 |
0,0 |
0,0 |
44,1 |
0,0 |
| Кукуруза 2 срока сева |
44,1 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
44,1 |
| Многолетние травы |
47,1 |
0,0 |
28,2 |
0,0 |
18,8 |
0,0 |
0,0 |
| Однолетние травы 1 срока сева |
21,4 |
0,0 |
0,0 |
21,4 |
0,0 |
0,0 |
0,0 |
| Однолетние травы 2 срока сева |
21,4 |
0,0 |
0,0 |
0,0 |
21,4 |
0,0 |
0,0 |
| Озимые на зеленый корм |
21,2 |
21,2 |
0,0 |
0,0 |
0,0 |
0,0 |
0,0 |
| Пастбища |
8,9 |
1,1 |
1,3 |
1,5 |
2,0 |
1,6 |
1,3 |
Таблица 6. Расчет выхода корма с 1 га кормовых угодий.
| Сельскохозяйственные культуры |
Содержится в 1 ц. корма |
Выход корма с 1 га, ц |
Основная продукция |
Побочная продукция |
Всего |
| Основная продукция |
Побочная продукция |
| ц.к.ед. |
переваримого протеина, кг |
ц.к.ед. |
переваримого протеина, кг |
основной |
побочной |
ц.к.ед. |
переваримого протеина, ц |
ц.к.ед. |
переваримого протеина, ц |
ц.к.ед. |
переваримого протеина, кг |
| Озимая пшеница товарная |
1,28 |
10,60 |
0,20 |
0,50 |
1,20 |
60,00 |
1,5 |
0,127 |
12,0 |
0,300 |
13,5 |
0,127 |
| Озимая пшеница фуражная |
1,28 |
10,60 |
0,20 |
0,50 |
37,50 |
60,00 |
48,0 |
3,975 |
12,0 |
0,300 |
60,0 |
3,975 |
| Ячмень товарный |
1,15 |
8,50 |
0,34 |
1,30 |
0,69 |
23,00 |
0,8 |
0,059 |
7,8 |
0,299 |
8,6 |
0,059 |
| Ячмень фуражный |
1,15 |
8,50 |
0,34 |
1,30 |
19,70 |
23,00 |
22,7 |
1,675 |
7,8 |
0,690 |
30,5 |
1,675 |
| Овес товарный |
1,00 |
7,90 |
0,31 |
1,70 |
0,78 |
26,00 |
0,8 |
0,062 |
8,1 |
0,442 |
8,8 |
0,062 |
| Овес фуражный |
1,00 |
7,90 |
0,31 |
1,70 |
23,58 |
26,00 |
23,6 |
1,863 |
8.1 |
0,442 |
31,6 |
1,863 |
| Горох товарный |
1,18 |
19,20 |
0,30 |
3,50 |
0,54 |
14,40 |
0,6 |
0,104 |
4,3 |
0,504 |
5,0 |
0,104 |
| Горох фуражный |
1,18 |
19,20 |
0,30 |
3,50 |
14,48 |
14,40 |
17,1 |
2,780 |
4,3 |
0,504 |
21,4 |
2,780 |
| Гречиха |
14,90 |
| Сахарная свекла |
0,16 |
1,90 |
91,20 |
14,6 |
1,733 |
14,6 |
| Подсолнечник |
| Кормовая свекла |
0,12 |
0,90 |
393,00 |
47,2 |
3,573 |
47,2 |
3,573 |
| Кукуруза на силос |
0,20 |
1,40 |
183,20 |
36,6 |
2,565 |
36,6 |
2,565 |
| Кукуруза на зеленый корм |
0,21 |
1,40 |
210,00 |
44,1 |
2,940 |
44,1 |
2,940 |
| Однолетние травы на сено |
0,45 |
6,70 |
37,00 |
16,7 |
2,479 |
16,7 |
2,479 |
| Однолетние травы на зеленый корм |
0,18 |
2,40 |
119,00 |
21,4 |
2,856 |
21,4 |
2,856 |
| Многолетние травы на сено |
0,50 |
9,90 |
25,00 |
12,5 |
2,475 |
12,5 |
2,475 |
| Многолетние травы на зеленый корм |
0,22 |
3,10 |
214,00 |
47,1 |
6,634 |
47,1 |
6,634 |
| Озимые на зеленый корм |
0,20 |
2,50 |
106,00 |
21,2 |
2,650 |
21,2 |
2,650 |
| Пар |
| Сенокосы |
0,48 |
4,00 |
25,00 |
12,0 |
1,000 |
12,0 |
1,000 |
| Пастбища |
0,27 |
3,00 |
33,00 |
8,9 |
0,990 |
8,9 |
0,990 |
| Молоко |
0,34 |
5,10 |
| Обрат |
0,13 |
3,50 |
В таблице 6 приведен расчет выхода корма с 1 га кормовых угодий.
Пределы насыщения севооборота отдельными культурами или группами культур определяются исходя из требований к рациональному чередованию сельскохозяйственных культур для данной зоны (табл. 7).
Таблица. 7 Пределы насыщения севооборотов отдельными культурами или группами культур
| Сельскохозяйственные культуры |
Нижняя граница |
Верхняя граница |
| % |
га |
% |
га |
| Всего пашни |
100% |
3 195 |
100% |
3195 |
| Зерновые |
50% |
1 598 |
60% |
1917 |
| Озимые |
20% |
639 |
30% |
959 |
| Гречиха |
0% |
0 |
5% |
160 |
| Сахарная свекла |
0% |
0 |
15% |
479 |
| Подсолнечник |
0% |
0 |
12% |
399 |
| Пар |
5% |
160 |
10% |
320 |
В таблице 8 приведены данные расчета потребности в кормах на 1 структурную голову при планируемом уровне продуктивности скота.
Таблица 8. Структура рационов и потребность в кормах в расчете на 1 структурную голову
 2.3. Запись экономико-математической модели в математическом виде 2.3. Запись экономико-математической модели в математическом виде
В данной задаче за основные неизвестные приняты площади посева сельскохозяйственных культур по их целевому назначению и площади сенокосов и пастбищ.
| x1
|
Озимая пшеница товарная |
| x2
|
Озимая пшеница фуражная |
| x3
|
Ячмень товарный |
| x4
|
Ячмень фуражный |
| x5
|
Овес товарный |
| x6
|
Овес фуражный |
| x7
|
Горох товарный |
| x8
|
Горох фуражный |
| x9
|
Гречиха |
| x10
|
Сахарная свекла |
| x11
|
Подсолнечник |
| x12
|
Кормовая свекла |
| x13
|
Кукуруза на силос |
| x14
|
Кукуруза на зеленый корм 1 срока сева |
| x15
|
Кукуруза на зеленый корм 2 срока сева |
| x16
|
Однолетние травы на сено |
| x17
|
Однолетние травы на зеленый корм 1 срока сева |
| x18
|
Однолетние травы на зеленый корм 2 срока сева |
| x19
|
Многолетние травы на сено |
| x20
|
Многолетние травы на зеленый корм |
| x21
|
Озимые на зеленый корм |
| x22
|
Пар |
| x23
|
Сенокосы |
| x24
|
Пастбища |
| x25
|
Молоко на корм |
| x26
|
Обрат |
| x27
|
Поголовье КРС |
| x28
|
Стоимость товарной продукции |
| x29
|
Производственные затраты |
| х30
|
Затраты труда |
На переменные накладываются следующие группы ограничений:
· по использованию земельных ресурсов;
· по определению стоимости товарной продукции;
· по определению потребности в трудовых ресурсах;
· по выполнению агротехнических требований возделывания сельскохозяйственных культур;
· по выполнению договорных обязательств по реализации продукции растениеводства;
· по обеспеченности потребностей животноводства кормами собственного производства;
· по поголовью сельскохозяйственных животных;
· по определению стоимости товарной продукции.
В процессе производственной деятельности используется три вида земельных ресурсов: пашня, сенокосы и пастбища.
Первое ограничение свидетельствует о том, что сумма всех посевных площадей и площади пара будет равна площади пашни:
Х1
+Х2
+ … +Х22
=3000 (1)
Второе и третье ограничения определяют полное использование соответствующего сенокосов (2) и пастбищ (3):
Х23
=250 (2)
Х24
=640 (3)
Четвертое ограничение служит для определения стоимости материально-денежных затрат. В качестве технико-экономических коэффициентов при переменных используются величина МДЗ (в тыс. руб.) в расчете на 1 га посева конкретных сельскохозяйственных культур и отдельных видов сельскохозяйственных животных:
3,0Х1
+3,0Х2
+2,6Х3
+ … + 0,3Х24
+14,2Х25
-Х29
=0 (4)
Пятое ограничение служит для определения потребности затрат труда по отрасли.. В качестве технико-экономических коэффициентов при переменных используются значения затрат труда (в чел-днях) в расчете на 1 га посева конкретных сельскохозяйственных культур и отдельных видов сельскохозяйственных угодий (графа 3 табл.1):
1,8Х1
+1,8Х2
+1,4Х3
+ … + 0,7Х23
+0,1Х24
-Х26
=0 (5)
Ограничения с 6 по 14 отражают требования по насыщению севооборотов отдельными культурами или группами культур. Пределы насыщения севооборотов отдельными культурами или группами культур приведены в табл.7.
Пятое и шестое ограничения описывают максимальную и минимальную границы насыщения севооборотов зерновыми культурами:
Х1
+Х2
+Х3
+ … + Х9
≥1500 (6)
Х1
+Х2
+Х3
+ … + Х9
≤1800 (7)
Седьмое и восьмое ограничения - озимыми культурами:
Х1
+Х2
≥600 (8)
Х1
+Х2
≤900 (9)
Девятое, десятое и одиннадцатое ограничения определяют верхние границы насыщения севооборота соответственно гречихой (10), сахарной свеклой (11) и подсолнечником (12):
Х9
≤150 (10)
Х10
≤450 (11)
Х11
≤360 (12)
Тринадцатое и четырнадцатое ограничения описывают максимальное и минимальное значение площади пара:
Х10
≥450 (13)
Х11
≤360 (14)
Пятнадцатое ограничение обеспечивает размещение озимых культур по рекомендуемым предшественникам. Технико-экономические коэффициенты перед переменными, обозначающими сельскохозяйственные культуры-предшественники, показывают возможность их использования в качестве предшественников. Так, по многолетним травам значение данных коэффициентов составляет 0,33. Это связано с тем, что в данном случае планируемый срок использования трав составляет три года, то есть ежегодно под посев озимых может быть отведено не более 1/3 их площадей.
Х1
+Х2
-Х7
-Х8
-Х14
-Х16
-Х17
-Х18
-0,33Х19
-0,33Х20
-Х22
≤0 (15)
Ограничения с 16 по 24 определяют гарантированные объемы производства товарной продукции. В качестве технико-экономических коэффициентов при переменных используются значения выхода товарной продукции с 1 га посева соответствующей сельскохозяйственной культуры (графа 7 табл.2). В правой части неравенства указывается плановый объем производства соответствующего вида продукции.
Например, ограничение по производству товарной пшеницы будет иметь вид:
31,45 Х1
≥20 000 (15)
Ограничения с 25 по 42 определяют гарантированные объемы производства кормов в соответствии с потребностями отрасли животноводства. В качестве технико-экономических коэффициентов при переменных используются значения выхода кормов с 1 га посева соответствующей сельскохозяйственной культуры (графы 5 и 6 табл.6) и затраты корма в кормовых единицах на 1 структурную голову КРС (табл. 7). По сельскохозяйственным культурам, являющихся источником получения зеленых кормов данные коэффициенты берутся из расчетной таблицы «Распределение зеленой массы кормовых культур по срокам использования».
Например:
ограничение по производству концентрированных кормов будет иметь вид:
1,1Х1
+32,5Х2
+0,8Х3
+24,7Х4
+0,8 Х5
+ 24,6 Х6
+0,8Х7
+21,5 Х8
-14,12 Х27
≥0 (27)
ограничение по производству соломы:
52,5Х1
+52,5Х2
+28Х3
+228Х4
+27 Х5
+ 27 Х6
+20Х7
+20 Х8
-4,01 Х27
≥0 (31)
Сорок третье ограничение описывает поголовье КРС в структурных головах.
Х27
≥450 (31)
Сорок четвертое ограничение предназначено для определения суммарной стоимости товарной продукции. В качестве технико-экономических коэффициентов при переменных используются выход товарной продукции с 1 га посева соответствующей сельскохозяйственной культуры в стоимостном выражении (графы 8 табл.12) и одной структурной головы КРС.
Целевая функции описывается как разница между стоимостью товарной продукции и сумой материально-денежных затрат:
Zm
ax
=Х28
-Х29
2.4. Запись экономико-математической модели в структурном виде
В структурном виде данную экономико-математическую модель можно представить следующим образом:
Минимизировать значение функции:
 , где , где
xs
- стоимость товарной продукции по хозяйству;
xz
– производственные затраты по хозяйству.
При условиях:
1. Оптимальный план должен исходить из наличия земельных ресурсов:
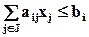 (iÎI), где (iÎI), где
аij
- затраты земельных ресурсов i-го вида на гектар посева j-й сельскохозяйственной культуры или на 1 голову j-го вида сельскохозяйственных животных.;
bi
- объем имеющихся земельных ресурсов i-го вида;
xj
- площадь посева j-той сельскохозяйственной.
2. Определение потребности в трудовых ресурсах:
 , где , где
tj
- затраты труда в расчете на 1 гектар посева j-й сельскохозяйственной культуры или на 1 голову j-го вида сельскохозяйственных животных.;
xt
- суммарные затраты труда по хозяйству
3. Определение суммы производственных затрат:
 , где , где
zj
– производственные затраты в расчете на 1 га посева j-ой сельскохозяйственной культуры или на 1 голову j-го вида сельскохозяйственных животных;
x
z
- суммарные производственные затраты по хозяйству
4. Выполнение агротехнических условий возделывания сельскохозяйственных культур:
4.1. Насыщение севооборотов отдельными культурами или группами культур
 (iÎI), где (iÎI), где
Qi
- верхние или нижние пределы насыщения севооборотов отдельными сельскохозяйственными культурами или группами культур.
4.2. Обеспеченность озимых культур предшественниками
 , где , где
xj
-площадь посева j-ой озимой культуры;
xj
p
- площадь посева j-ой сельскохозяйственной культуры;
αj
- коэффициент возможного использования посевов j-ой сельскохозяйственной культуры в качестве предшественника под озимые.
5. Выполнение заказа на производство товарной продукции
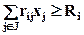 (iÎI), где (iÎI), где
rij
– выход товарной продукции i-го вида с 1 га посева j-й сельскохозяйственной культуры или с 1 головы j-го вида сельскохозяйственных животных;
R
j- планируемый объем реализации продукции i-го вида.
6. Производство кормов должно полностью удовлетворять потребности отрасли животноводства в собственных кормах
 (iÎI), где (iÎI), где
kij
– выход корма i-го вида с 1 га посева j-й сельскохозяйственной культуры;
dij
– потребность в корме i-го вида на 1 голову j-го вида сельскохозяйственных животных;
7. Определение стоимости товарной продукции
 , где , где
sj
- выход товарной продукции в денежном выражении с 1 га посева j-й сельскохозяйственной культуры или с 1 головы j-го вида сельскохозяйственных животных;
xs
- стоимость товарной продукции по хозяйству
8. Определение поголовья
 , где , где
Gi
–минимальное поголовье крупного рогатого скота
9. Переменные величины не могут иметь отрицательного значения

2.5. Запись экономико-математической модели в матричном виде
Разработанная экономико-математическая модель в матричном виде представлена в таблице 9.
3. Анализ результатов решения экономико-математической задачи по оптимизации отраслевой структуры производства в СХА «Горизонт»
Данная задача была реализована в 3 вариантах. В первом варианте поголовье КРС бралось на фактическом уровне, во втором на уровне 80% от фактического показателя, в третьем – 120%.
В результате анализа вариантов ( см. табл. 10) можно сделать следующие выводы: при изменении поголовья КРС изменяется и структура посевных площадей. В первую очередь это связано с необходимостью получения корма для животных. При увеличении кол-ва КРС площадь под кормовые культуры увеличивается, а структура посевных площадей под зерновые культуры терпит изменение в сторону уменьшения, т.к. общая площадь пашни в хозяйстве не изменяется.
Значительные изменения происходят и в объемах производства продукции и ее реализации. Т.к. изменение поголовья КРС приводит напрямую к изменению кол-ва молока, производимого хозяйством и прироста КРС. С этим связано уменьшение стоимости товарной продукции при уменьшении кол-ва КРС и наоборот ее увеличение при увеличении поголовья скота. Однако т.к. МТЗ и трудоемкость выращивания КРС достаточно велики, то уровень рентабельности в хозяйстве максимальный при уменьшении поголовья КРС на 20% и именно этот вариант дает максимальную прибыль.
Выводы и предложения
Методы планирования характеризуются всеми теми положительными моментами, которые присущи им: они используют те же нормативы, экономико-математическое моделирование и реализация расчетов на ЭВМ, открывают неограниченные возможности в получении необходимого количества вариантов плана. При решении экономико-математических задач все вопросы решаются в строго количественных пропорциях между всеми сторонами производства в единой балансовой взаимоувязке между ними. Преимущество их состоит в обеспечении оптимальных решений, а реализация их на ЭВМ позволяет получать эти решения за короткий промежуток времени. При этом обеспечивается экономическая оценка плана как единого комплекса отраслей с учетом всех воздействующих на него факторов.
Результаты решения экономико-математической модели показали, что хозяйства в настоящее время обеспечены техникой и сельскохозяйственными машинами лишь на одну треть.
Одной из основных причин сокращения сельскохозяйственного производства являются значительные сбои в материально-техническом обеспечении сельского хозяйства. По данным Госкомстата, за последние годы парк основных видов сельскохозяйственной техники сократился до 40% и составил по основным машинам около 55-65% от нормативного. Машинно-тракторный парк "состарился", 42% тракторов работает сверх амортизационного срока, из остальных - 70% эксплуатируется по 8-10 лет. Еще хуже положение с комбайнами. Сверх амортизационного срока эксплуатируется 65% зерноуборочных комбайнов.
Чтобы обеспечить хозяйства недостающей техникой необходимы большие инвестиции.
Аналогичная ситуация с дефицитом техники и сельхозмашин характерна для хозяйств всей страны. Разумеется, хозяйства самостоятельно не в состоянии произвести инвестиции. Одним из способов выхода из создавшейся ситуации является теснейшая интеграция сельскохозяйственных предприятий с сильными перерабатывающими предприятиями.
Агропромышленному комплексу страны необходимо учитывать накопленный положительный опыт передовых хозяйств в деле возрождения сельского хозяйства путем интеграции предприятий АПК.
Список используемой литературы
1. Богданов Г.А. Кормление сельскохозяйственных животных. - М.: ВО "Агропромиздат", 1990. - 624 с.
2. Гатаулин А.М. Математическое моделирование экономических процессов в сельском хозяйстве. - М.: ВО "Агропромиздат", 1990. - 432с.
3. Курносов А.П. Вычислительная техника и программирование. - М.: "Финансы и статистика", 1991. - 344с.
4. Курносов А.П. Разработка экономико-математической модели по определению оптимально специализации и сочетания отраслей в сельскохозяйственных предприятиях. Лекция - Воронеж, - 1988
5. Методы решения задач математического программирования. Учебное пособие / А.П. Курносов, В.П. Подтележников. - Воронеж: ВСХИ, 1990. - 108с.
6. Муравьев А.С., Олейник Г.Г. Нормативньй справочник по экономике и организации сельскохозяйственного производства. М.: Колос, 1972
7. Муртаф Брюс. Современное линейное программирование. Теория и практика: пер. с англ. / под. ред. И.А. Станевичюса. - : Мир, 1984. - 224с.
8. Немчинов В.С. Экономико-математические методы и модели. М.: Мысль, 1965. - 478с.
9. Нормативная информация для разработки технологических карт в животноводстве с использованием ЭВМ (Сост. Терновых К.С., Дубровский Б.А., Саввин А.В. и др.). - Воронеж. 1996. - 71с.
10. Нормы и рационы кормления сельскохозяйственных животных. /А.П. Калашников, Н.И. Клейшенов и др. - М.: 1986. - 352с.
11. Разработка экономико-математической модели по определению оптимальной специализации и сочетания отраслей в сельскохозяйственных предприятиях / А.П. Курносов. Лекция. - Воронеж, ВСХИ, 1988. - 50с.
12. Решение экономико-математических задач на персональном компьютере. Учебное пособие. / А.П. Курносов, А.В. Агибалов. - Воронеж, ВСХИ, 1992. - 75с.
13. Справочник по планированию и экономике сельскохозяйственного производства: в 2-х ч. Ч.1, Ч.2/Сост. Г.В. Кулик, Н.А. Окунь, Ю.М. Пехтерев. - М.: Россельхозиздат. - 512с.
[1]
Немчинов В.С. «Экономико-математические методы и модели. М.:, 1967, с. 161.
[2]
Тунеев М.М., Сухоруков В.Ф. Экономико-математические методы в организации и планировании сельскохозяйственного производства: Учеб пособие, М.:, 1986, с. 7.
[3]
Тунеев М.М., Сухоруков В.Ф. Экономико-математические методы в организации и планировании сельскохозяйственного производства: Учеб пособие, М.:, 1986, с. 12.
|