| Министерство образования Республики Беларусь
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное учреждение высшего профессионального образования
БЕЛОРУССКО–РОССИЙСКИЙ УНИВЕРСИТЕТ
Кафедра «Автоматизированные системы управления»
Курсовая работа на тему:
«Исследование алгоритма SSA-метода при анализе временных последовательностей данных с шумом по известному закону распределения»
по дисциплине
«Математическая логика и теория алгоритмов»
051.23 02 01.081446.23.81-01
2010
Задание на курсовую работу по дисциплине «Математическая логика и теория алгоритмов»
1 Тема работы
: Исследование алгоритма SSA-метода при анализе временных последовательностей данных с шумом по известному закону распределения.
2 Срок сдачи студентом законченной работы ‑ 25.05.2010 г.
3 Исходные данные для работы:
1) Технология исследования SSA-метода с использованием пакетов MS Excel, Mathcad, Statistica. 2) Алгоритм генерации временной последовательности данных по заданному закону распределения:
Постановка задачи.
Исследовать свойства SSA-метода при декомпозиции временной последовательности данных на трендовую, гармоническую и шумовую составляющие. Оценить погрешность SSA-метода при декомпозиции временной последовательности данных для разных значений тренда, гармоники и шума. Восстановление шумовой составляющей оценить по критериям хи-квадрат Пирсона, лямбда Колмогорова, омега-квадрат Мизеса.
4 Содержание расчётно-пояснительной записки.
Титульный лист.
Задание на курсовую работу. Аннотация.
Содержание. Перечень условных обозначений. Введение. 1 Анализ и теоретическое исследование алгоритма. 2 Разработка технологии экспериментального исследования алгоритма. 3 Описание разработанного программного обеспечения. 4 Экспериментальное исследование алгоритма. Заключение. Список использованных источников. Приложение.
5. Дата выдачи задания 22.02.2010 г.
6. Научный консультант: канд. техн. наук, доц. Альховик С. А.
7. Календарный график работы на весь период проектирования.
Оглавление
Введение
1. Распределение Pearson Type V
1.1 Формализованное описание закона Pearson Type V
1.2 Примеры использования закона распределения Pearson Type V
1.3 Числовые характеристики закона распределения Pearson Type V
1.4 Получение выборки с распределением Pearson Type V
1.5 Формулировка гипотезы о законе распределения Pearson Type V
1.6 Проверка гипотезы о законе распределения Pearson Type V
1.7 Программа для проверки гипотезы о законе распределения
2. Распределение Rayleigh
2.1 Формализованное описание закона Rayleigh
2.2 Примеры использования закона распределения Rayleigh
2.3 Числовые характеристики закона распределения Rayleigh
2.4 Получение выборки с распределением Rayleigh
2.5 Формулировка гипотезы о законе распределения Rayleigh
2.6 Проверка гипотезы о законе распределения Rayleigh
2.7 Программа для проверки гипотезы о законе распределения
3. SSA-метод
3.1 Определение собственных чисел матрицы
3.2 Содержательное описание SSA-метода
3.3 Методика исследования SSA-метода на основе информационных технологий
4. Исследование временных рядов с шумом заданным Pearson Type V
4.1 Постановка эксперимента
4.2 Экспериментальная часть (тренд)
4.3 Экспериментальная часть (гармонический ряд)
4.4 Экспериментальная часть (рандом)
4.5 Результаты и их обсуждение
5. Исследование временных рядов с шумом заданным Rayleigh
5.1 Постановка эксперимента
5.2 Экспериментальная часть (тренд)
5.3 Экспериментальная часть (гармонический ряд)
5.4 Экспериментальная часть (рандом)
5.5 Результаты и их обсуждение
6. Экспериментальное исследование средней трудоемкости Pirson Type V
7. Экспериментальное исследование средней трудоемкости Rayleigh
Заключение
Список использованных источников
Введение
В процессе интеллектуального анализа данных (ИАД) центральное место занимает автоматическое порождение характеризующих анализируемые данные моделей, правил и/или функциональных зависимостей. В целом процесс извлечения знаний в ИАД условно делят на следующие этапы, которые в совокупности предложено использовать на этапе эксплуатации имитационной модели (ИМ) сложного объекта.
Шаг 1. Отбор данных: анализ задач пользователя, выбор целевого множества данных, определение переменных.
Шаг 2. Предобработка данных: устранение зашумленности, обработка пропущенных значений, итоговые показатели по группам данных.
Шаг 3. Редукция и проекция данных: ищутся полезные особенности данных для решения поставленных задач, сокращается пространство переменных.
Шаг 4. Поиск закономерностей: выбор метода поиска закономерностей с учетом объема и типа данных, их зашумленности и осуществление поиска закономерностей.
Шаг 5: Оценка и интерпретация найденных закономерностей: оценка и упорядочение закономерностей по их релевантности, проверка согласованности предыдущих и вновь найденных знаний. Возможно возвращение к любому шагу от 1 до 4 для дальнейших итераций.
Шаг 6. Использование найденных знаний: прямое использование, передача заинтересованным лицам, включение в интеллектуальные системы, основанные на знаниях.
Для разработки технологии извлечения знаний из временных последовательностей данных исследован сингулярный спектральный метод (SSA-метод), включающий этапы вложения, сингулярного разложения, группировки, диагонального усреднения. Исследуем Pearson Type V и Rayleigh законы распределения.
1. Распределение Pearson Type V
1.1 Формализованное описание закона Pearson Type V распределения случайной величины
Плотность вероятности
если x>0;

в противном случае
Функция распределения
если x>0;

где  функция распределения случайной величины с распределением gamma( функция распределения случайной величины с распределением gamma( ,1/ ,1/ ) )
График функции плотностей распределения вероятностей PT5(α,1) представлен на рисунке 1.1.

Рисунок 1.1. Функции плотностей распределения вероятностей PT5(α,1)
1.2 Примеры использования закона распределения Pearson Type V
Варианты применения: Время выполнения какой-либо задачи (График функции плотности принимает форму, подобную форме графика плотности логнормального распределения, но может иметь большой острый “выступ” ближе к х=0)
1.3 Числовые характеристики закона распределения Pearson Type V
Параметр формы α > 0, масштабный параметр β > 0
Область[0,∞)
Среднее для α > 1 для α > 1
Дисперсия для α > 2 для α > 2
Мода
Оценка максимального правдоподобия
При наличии данных Х
1, Х
2, …, Х
n
подборка распределения gamma( , , ) к 1/Х
1, 1/Х
2, …, 1/Х
n
,
в результате дает оценки по методу максимального правдоподобия ) к 1/Х
1, 1/Х
2, …, 1/Х
n
,
в результате дает оценки по методу максимального правдоподобия  и и  . Оценки максимального правдоподобия для PT5(α,β) составляют . Оценки максимального правдоподобия для PT5(α,β) составляют  = = и
и  = =
Примечания1. Тогда и только тогда X~ PT5(α,β), когда Y=1/X~gamma( ,1/ ,1/ ). Поэтому распределение Пирсона типа V называют обращенным гамма - распределением. ). Поэтому распределение Пирсона типа V называют обращенным гамма - распределением.
2. Заметьте, среднее и дисперсия существуют только для определенных значений параметров формы.
1.4 Получение выборки с распределением Pearson Type V
Текст программы на C++
//kursml.cpp : main project file.
#include "stdafx.h"
#include "Pearson5.h"
using namespace System;
using namespace Variates;
using namespace System::IO;
int main(array<System::String ^> ^args)
{
TextWriter ^tr = File::CreateText(L"numbers.txt");
for(int i=0;i<100;i++)
{
tr->WriteLine((Pearson5::Sample(1,1).ToString());
}
tr->Close();
return 0;
}
Pearson5.h
#pragma once
#include "Rng.h"
#include "Gamma.h"
using namespace System;
namespace Variates
{
public ref class Pearson5 : public Rng
{
private:
double m_alpha;
double m_beta;
public:
Pearson5(double alpha, double beta) : m_alpha(alpha), m_beta(beta)
{}
virtual double Sample() override
{
return Sample(m_alpha, m_beta);
}
static double Sample(double alpha, double beta)
{
return 1 / Gamma::Sample(alpha, 1 / beta);
}
//FG(x) функция распределения случайной велечины с распределением GAMMA(gamma,1/beta)
virtual double DistributionFunction(double x) override
{return Pearson5::DistributionFunction(x, m_alpha, m_beta);}
//функция распределения F(x)
static double DistributionFunction(double x, double alpha, double beta)
{if (x > 0)
{return 1 - Gamma::DistributionFunction(1/x, alpha, 1/beta);//F(x)=1-FG(1/x)
}
else {return 0;}
}
virtual double DensityFunction(double x) override
{return Pearson5::DensityFunction(x, m_alpha, m_beta);}
//плотность f(x)
static double DensityFunction(double x, double alpha, double beta)
{if (x > 0)
{return Math::Pow(x, -(alpha + 1)) * Math::Exp(-beta / x) / Math::Pow(beta, -alpha) / Gamma::GammaFunction(alpha);}
else {return 0;}
}
};
}
Полученный по этой функции ряд представлен следующими значениями: (Объем выборки равен 43. Это ограничение обусловлено последующим использованием пакета Mathcad, в котором общее число элементов матрицы не должно превышать числа 600)
1,4898437906868
0,155118334154153
0,61232084606753
2,93030830346735
0,805146083946738
9,56457213164303
1,27783343504077
0,251137603293805
3,5276740403232
1,87120717537695
1,32530533009446
0,580380148657655
2,75653644757967
1,17443969975235
40,4251902165006
0,819370739897353
0,76435890601386
0,294787757136549
7,05592655012343
2,66917981096155
8,79281345418844
0,580093474185326
1,39633930229403
2,53700526140079
0,770494926092603
1,93265448451382
1,18590055703106
1,0792114387216
0,82818491346851
1,7150955462617
2,95934460597946
2,25523634892915
0,235192957404532
1,90816102397495
0,459223533552272
1,2301015212362
0,461599593338555
5,8725267553485
0,405012588940358
0,697295973424586
1,10547514222875
5,24774803293084
0,650277052201361
1.5 Формулировка гипотезы о законе распределения Pearson Type V
Пусть f0
(x) – известная плотность вероятности распределения Pearson Type V и fξ
(x) – плотность вероятности генеральной совокупности.
Гипотеза вида
{H0
: fξ
(x) = f0
(x); H1
: fξ
(x) ≠ f0
(x);}
Является двухальтернативной непараметрической сложной гипотезой о законе распределения. Здесь проверяется утверждение о том, что исследуемая выборка извлечена из распределения f0
(x)
Для проверки согласия полученных случайных величин теоретическому распределению используется λ-критерий Колмогорова–Смирнова. Критерий Колмогорова–Смирнова применяется с наибольшей эффективностью, когда есть основание предположить, что частоты каждого из порядковых значений будут располагаться не случайным образом, а в соответствии с некоторой предсказуемой схемой.
Процедура, связанная с вычислением тестовой статистики λ, требует накапливания частот по всем порядковым значениям. Затем сравниваются два распределения накопленных частот – теоретическое распределение, имеющее место при справедливой H0
, и наблюдаемое распределение. Таким образом, проверяется гипотеза
H0
: Fξ
(x) = F0
(x),
против альтернативы
H1
: Fξ
(x) ≠ F0
(x),
где Fξ
(x) – функция распределения генеральной совокупности, F0
(x) – непрерывная гипотетическая функция распределения.
Для проверки гипотезы используется статистика
 , ,
где Δ – максимальный модуль отклонения гипотетической функции распределения от эмпирической функции распределения
 . .
Если гипотеза H0
верна, то статистика λ имеет распределение, приближающееся при  к распределению Колмогорова–Смирнова. Критерий для проверки гипотезы имеет следующий вид: к распределению Колмогорова–Смирнова. Критерий для проверки гипотезы имеет следующий вид:
P(λ > λα
) = α,
где α – 100α-процентное отклонение распределения Колмогорова–Смирнова. Например, для α = 0,01 критическое значение статистики λα
= 1,627.
Для последовательности (выборки) данные сгруппированы для проведения расчетов по критерию согласия Колмогорова–Смирнова.
Г. Стерджес (Herbert Sturges, 1926) предложил правило для определения числа интервалов k при построении гистограммы распределения случайной величины. При этом i-й интервал является биномиальным коэффициентом  . Общий объем выборки . Общий объем выборки
 , ,
отсюда число интервалов для построения гистограммы с нормальными данными
 , ,
где n – количество значений случайной величины в исследуемой выборке. Полученное значение округляется до целого числа. Правило Г. Стерджеса справедливо для величин, распределенных по нормальному закону. В общем случае оно может быть использовано без корректировки для n < 200 [6]. При использовании десятичного логарифма, соответственно, используется формула
 . .
Для построения гистограммы и проверки гипотезы о законе распределения Pearson Type V построена таблица 1.
Таблица 1 – Исходные данные для построения гистограммы и проверки гипотезы о законе распределения Pearson Type V
| №
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
| ξi
|
0-5,857
|
5,857-11,714
|
11,714-17,571
|
17,571-23,428
|
23,428-29,285
|
29,285-35,142
|
35,142-41
|
| Fξ
|
38
|
4
|
0
|
0
|
0
|
0
|
1
|
1.6 Проверка гипотезы о законе распределения Pearson Type V
Для проверки гипотезы о законе распределения выполняется следующая последовательность шагов.
Шаг 1. Находим ожидаемую частоту ni
0
путем вычисления в Mathcad интеграла функции плотности вероятности на каждом из интервалов. Результат представлен на рисунках 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8.

Рисунок 1.2. Ожидаемая вероятность на интервале 0 - 5,857

Рисунок 1.3. Ожидаемая вероятность на интервале 5,857-11,714

Рисунок 1.4. Ожидаемая вероятность на интервале 11,714-17,571

Рисунок 1.5. Ожидаемая вероятность на интервале 17,571-23,428

Рисунок 1.6. Ожидаемая вероятность на интервале 23,428-29,285

Рисунок 1.7. Ожидаемая вероятность на интервале 29,285-35,142

Рисунок 1.8. Ожидаемая вероятность на интервале 35,142 – 41
Шаг 2. Выражаем каждую наблюдаемую и каждую ожидаемую частоту в виде отношения:
частота клетки
n
Шаг 3. Вычисляем накопленные значения наблюдаемых и ожидаемых отношений путем их суммирования слева направо (суммирование справа налево также приводит к статистике λ).
Шаг 4. Находим абсолютные значения разности между накопленными наблюдаемыми отношениями и накопленными ожидаемыми отношениями.
Шаг 5. Находим наибольшее отношение и выражаем его в виде десятичной дроби. Полученное значение соответствует тестовой статистике λ. В данном примере наибольшее отношение равно Δ =0,058744186.
Шаг 6. В таблице Е [4, с. 141] (критические значения Δα
в критерии Колмогорова–Смирнова для одной выборки) при объеме выборки свыше 35 предлагается определять критическое значение Δα
при α = 0,01 по формуле
 . .
Если наблюдаемое значение Δ больше или равно критическому значению, H0 отклоняется. В данном примере критическое значение
Δ
α
=0,249. Поскольку наблюдаемое значение Δ меньше критического, H0 принимается.
1.7 Программа для проверки гипотезы о законе распределения
Проверка гипотезы о законе распределения выполнена в электронной таблице MS Excel. Случайные величины эмпирического распределения расположены в ячейках B2:B44. Рабочее поле для выполнения расчетов расположено в ячейках E4:K11.

Рисунок 1.9. Проверка гипотезы о законе распределения, выполненная в электронной таблице MS Excel
2. Распределение Rayleigh
2.1 Формализованное описание закона Rayleigh распределения случайной величины
Плотность вероятности

где a – параметр масштаба, мода (а>0)
Функция распределения

Функция риска

График функции плотностей распределения вероятностей Rayleigh представлен на рисунке 2.1.

Рисунок 2.1. Функции плотностей распределения вероятностей Rayleigh
2.2 Примеры использования закона распределения Rayleigh
Варианты применения: Время выполнения какой-либо задачи.
2.3 Числовые характеристики закона распределения Rayleigh
Математическое ожидание
Медиана
Мода
Дисперсия
Стандартное отклонение
Коэффициент вариации
Асимметрия
Эксцесс
р-квантиль
2.4 Получение выборки с распределением Rayleigh
Генерирование случайных чисел
x = =
Текст программы на C++
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#include<time.h>
#include<math.h>
int main()
{FILE *f;
int i;
const int a=1;
float m[43];
if((f=fopen("43.txt","wb"))==NULL)
{printf("!!Cann't write file!!\n");exit(1);}
else printf("Can write file 43.txt\n");
printf("\n");
srand(time(NULL));
for(i=0;i<43;i++)
{
m[i]=a*sqrt( (-2)*log(float(rand())/RAND_MAX) );
printf("%f \n",m[i]);
fprintf(f,"%f \n",m[i]);
}
fclose(f);
return 0;}
Полученный по этой функции ряд представлен следующими значениями:
1.844905 2.870072 1.764507 1.110845 1.526675 0.788239 0.816683 1.968559 0.525110 0.797883 1.464174 1.080738 1.356594 0.425269 1.633723 3.143837 1.242856 1.467282 1.063998 2.868115 0.975500 1.288683 1.921442 0.605059 0.716165 2.192975 2.094303 1.237865 0.902787 1.665678 1.110946 1.694965 0.569614 1.908184 1.234843 1.612594 0.508507 0.355821 0.721552 0.678204 0.108697 1.029705 0.827769
Объем выборки равен 43. Это ограничение обусловлено последующим использованием пакета Mathcad, в котором общее число элементов матрицы не должно превышать числа 600.
2.5 Формулировка гипотезы о законе распределения Rayleigh
Пусть f0
(x) – известная плотность вероятности распределения Rayleigh и fξ
(x) – плотность вероятности генеральной совокупности.
Гипотеза вида
{H0
: fξ
(x) = f0
(x); H1
: fξ
(x) ≠ f0
(x);}
Является двухальтернативной непараметрической сложной гипотезой о законе распределения. Здесь проверяется утверждение о том, что исследуемая выборка извлечена из распределения f0
(x)
Для проверки согласия полученных случайных величин теоретическому распределению используется λ-критерий Колмогорова–Смирнова. Критерий Колмогорова–Смирнова применяется с наибольшей эффективностью, когда есть основание предположить, что частоты каждого из порядковых значений будут располагаться не случайным образом, а в соответствии с некоторой предсказуемой схемой.
Процедура, связанная с вычислением тестовой статистики λ, требует накапливания частот по всем порядковым значениям. Затем сравниваются два распределения накопленных частот – теоретическое распределение, имеющее место при справедливой H0
, и наблюдаемое распределение. Таким образом, проверяется гипотеза
H0
: Fξ
(x) = F0
(x),
против альтернативы
H1
: Fξ
(x) ≠ F0
(x),
где Fξ
(x) – функция распределения генеральной совокупности, F0
(x) – непрерывная гипотетическая функция распределения.
Для проверки гипотезы используется статистика
 , ,
где Δ – максимальный модуль отклонения гипотетической функции распределения от эмпирической функции распределения
 . .
Если гипотеза H0
верна, то статистика λ имеет распределение, приближающееся при  к распределению Колмогорова–Смирнова. Критерий для проверки гипотезы имеет следующий вид: к распределению Колмогорова–Смирнова. Критерий для проверки гипотезы имеет следующий вид:
P(λ > λα
) = α,
где α – 100α-процентное отклонение распределения Колмогорова–Смирнова. Например, для α = 0,01 критическое значение статистики λα
= 1,627.
Для последовательности (выборки) данные сгруппированы для проведения расчетов по критерию согласия Колмогорова–Смирнова.
Г. Стерджес (Herbert Sturges, 1926) предложил правило для определения числа интервалов k при построении гистограммы распределения случайной величины. При этом i-й интервал является биномиальным коэффициентом  . Общий объем выборки . Общий объем выборки
 , ,
отсюда число интервалов для построения гистограммы с нормальными данными
 , ,
где n – количество значений случайной величины в исследуемой выборке. Полученное значение округляется до целого числа. Правило Г. Стерджеса справедливо для величин, распределенных по нормальному закону. В общем случае оно может быть использовано без корректировки для n < 200. При использовании десятичного логарифма, соответственно, используется формула
 . .
Для построения гистограммы и проверки гипотезы о законе распределения Rayleigh построена таблица 2.
Таблица 2 – Исходные данные для построения гистограммы и проверки гипотезы о законе распределения Rayleigh
| №
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
| ξi
|
0-0.448
|
0.448-0.896
|
0.896-1.344
|
1.344-1.792
|
1.792-2.24
|
2.24-2.688
|
2.688-3.14
|
| Fξ
|
3
|
11
|
11
|
9
|
6
|
0
|
3
|
2.6 Проверка гипотезы о законе распределения Rayleigh
Для проверки гипотезы о законе распределения выполняется следующая последовательность шагов.
Шаг 1. Находим ожидаемую частоту ni
0
путем вычисления в Mathcad интеграла функции плотности вероятности на каждом из интервалов. Результат представлен на рисунках 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8.

Рисунок 2.2. Ожидаемая вероятность на интервале 0 - 0,448

Рисунок 2.3. Ожидаемая вероятность на интервале 0,448-0,896

Рисунок 2.4. Ожидаемая вероятность на интервале 0,896-1,344

Рисунок 2.5. Ожидаемая вероятность на интервале 1,344-1,792

Рисунок 2.6. Ожидаемая вероятность на интервале 1,792-2,240

Рисунок 2.7. Ожидаемая вероятность на интервале 2,240-2,688

Рисунок 2.8. Ожидаемая вероятность на интервале 2,688 - 3.14
Шаг 2. Выражаем каждую наблюдаемую и каждую ожидаемую частоту в виде отношения:
частота клетки
n
Шаг 3. Вычисляем накопленные значения наблюдаемых и ожидаемых отношений путем их суммирования слева направо (суммирование справа налево также приводит к статистике λ).
Шаг 4. Находим абсолютные значения разности между накопленными наблюдаемыми отношениями и накопленными ожидаемыми отношениями.
Шаг 5. Находим наибольшее отношение и выражаем его в виде десятичной дроби. Полученное значение соответствует тестовой статистике λ. В данном примере наибольшее отношение равно Δ =0,04226744.
Шаг 6. В таблице Е [4, с. 141] (критические значения Δα
в критерии Колмогорова–Смирнова для одной выборки) при объеме выборки свыше 35 предлагается определять критическое значение Δα
при α = 0,01 по формуле
 . .
Если наблюдаемое значение Δ больше или равно критическому значению, H0 отклоняется. В данном примере критическое значение Δα
=0,249. Поскольку наблюдаемое значение Δ меньше критического, H0 принимается.
2.7 Программа для проверки гипотезы о законе распределения
Проверка гипотезы о законе распределения выполнена в электронной таблице MS Excel. Случайные величины эмпирического распределения расположены в ячейках B2:B44. Рабочее поле для выполнения расчетов расположено в ячейках E4:K11.

Рисунок 2.9. Проверка гипотезы о законе распределения, выполненная в электронной таблице MS Excel
3.
SSA-метод
3.1 Определение собственных чисел матрицы
Предположим, что  и и  . Вектор . Вектор  принадлежит принадлежит  и будет элементом из области значений матрицы А. Нам будут особенно интересны те векторы x, которые при умножении на А переходят в кратные им векторы, т.е. такие векторы и будет элементом из области значений матрицы А. Нам будут особенно интересны те векторы x, которые при умножении на А переходят в кратные им векторы, т.е. такие векторы  , для которых существует число , для которых существует число  из из 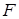 с с 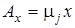 . Такой ненулевой вектор . Такой ненулевой вектор 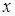 называется правым собственным вектором матрицы называется правым собственным вектором матрицы 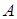 и и  – соответствующим собственным значением. – соответствующим собственным значением.
Написанное выше уравнение может быть переписано в виде
 . .
Причем 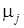 – собственное значение матрицы – собственное значение матрицы 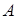 в том и только в том случае, когда в том и только в том случае, когда 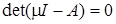 . Определение функции определения означает теперь, что . Определение функции определения означает теперь, что 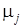 удовлетворяет полиномиальному уравнению с коэффициентом в удовлетворяет полиномиальному уравнению с коэффициентом в 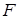 , это уравнение известно как характеристическое уравнение матрицы , это уравнение известно как характеристическое уравнение матрицы 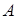 . Многочлен . Многочлен  называется характеристическим многочленом матрицы называется характеристическим многочленом матрицы 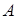 . .
Следует заметить, что правый собственный вектор матрицы  , соответствующий данному собственному значению , соответствующий данному собственному значению 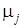 не может быть единственным. Правые собственные векторы соответствуют в действительности с множеством всех ненулевых элементов из не может быть единственным. Правые собственные векторы соответствуют в действительности с множеством всех ненулевых элементов из  . .
Отметим что величина
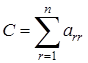
известна как след матрицы  и обозначается через и обозначается через  . .
Если  – собственные значения матрицы – собственные значения матрицы  (не обязательно различные), то (не обязательно различные), то
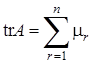 ; ;
 . .
Пример
. Показать, что для матрицы
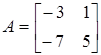
собственными значениями будут 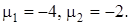
Решение:
 ; ;
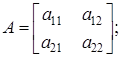  ; ;
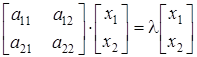 ; ;
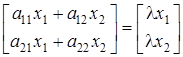 . .
Две матрицы равны, если равны их соответствующие элементы, поэтому
 ; ;
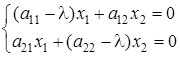 . .
Решаем систему уравнений методом Гаусса:
 ; ;
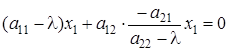 ; ;
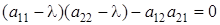 ; ;
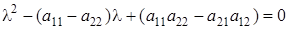 ; ;
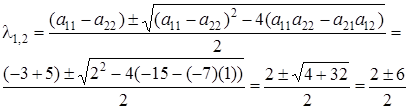 ; ;
 . .
Найдем правые собственные вектора, соответствующие собственным числам.
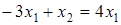 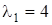 . .
Откуда
 . .
Пусть вектор  . .
Проверим
 ; ;
 или или 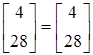 . .
 ; ;  . .
Откуда

Пусть
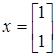 . .
Проверим
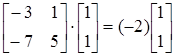 ; ;
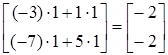 или или  = = . .
3.2 Содержательное описание
SSA-метода
Метод SSA используется для анализа временных рядов и может быть использован на каждом из этапов эксплуатации ИМ. Он позволяет выделить ряды, которые описывают тренд первоначального ряда, гармонические колебания и те составляющие рядов, которые относят к «шуму». При этом метод не требует стационарности ряда, знания модели тренда, а также сведений о наличии в ряде периодических составляющих и их периодах. Также с помощью данного метода можно определить модель тренда и использовать это знание для дальнейшей обработки ряда уже с известной моделью тренда, что важно, например, при автоматизации определения длительности переходного процесса в ИМ.
Математической основой метода SSA является сингулярное разложение [4]. Для успешного применения метода SSA следует последовательно пройти несколько шагов.
Вложение. На этом шаге выбирается ширина окна L, от выбора которой зависят результаты применения метода SSA. Из-за того, что нет общих рекомендаций по выбору ширины окна, параметр L зависит от решаемой задачи и предварительной информации, известной о ряде. Например, для выделения тренда рекомендуется выбирать ширину окна не слишком большой. С другой стороны, для выделения гармонических колебаний рекомендуется большая ширина окна. После выбора ширины окна в соответствии с L строится траекторная матрица А ряда, которая будет являться по условию её построения ганкелевой [5].
Сингулярное разложение. Для матрицы S = A·AT
находятся собственные числа λ и ортонормированные собственные вектора U. Упорядоченные по убыванию собственные числа, которые являются большими нуля, часто называются сингулярными числами, а соответствующие им собственные вектора – левыми сингулярными векторами U. После этого вычисляются вектора V, которые называются правыми сингулярными векторами, и находятся элементарные матрицы, на сумму которых раскладывается первоначальная траекторная матрица.
Группировка. На этапе группировки элементарные матрицы группируются по принципу принадлежности к тренду, гармоническим колебаниям или к шуму. Этот этап является наиболее сложным при применении метода SSA. Для нахождения тренда на диаграммах собственных векторов (по оси абсцисс откладывается порядковый номер координаты собственного вектора, по оси ординат откладывается значение координаты собственного вектора) выделяют медленно меняющиеся вектора. Сумма элементарных матриц, соответствующих этим векторам будет являться траекторной матрицей тренда ряда. После этого восстанавливают гармонические колебания ряда. Для отделения шума можно воспользоваться несколькими замечаниями: нерегулярное поведение сингулярных векторов может говорить о принадлежности их к набору, порожденному шумовой компонентой; также об этом может свидетельствовать медленное, практически без скачков, убывание собственных значений с некоторого номера.
Диагональное усреднение. Если полученные сгруппированные матрицы являются ганкелевыми, то они являются траекторными матрицами некоторого ряда, который может быть легко по ним восстановлен. Однако обычно сгруппированные матрицы редко получаются ганкелевыми, поэтому для восстановления ряда прибегают к диагональному усреднению. В соответствии с этим этапом каждый член восстановленного ряда будет являться средним арифметическим соответствующей ему побочной диагонали траекторной матрицы.
В результате проделанных шагов получается несколько рядов, один из которых является рядом, описывающим тренд первоначального ряда, другой описывает гармонические колебания, а третий – шумовые составляющие.
3.3 Методика исследования
SSA-метода на основе информационных технологий
Для исследования SSA-метода применяется комплекс информационных технологий, представленный табличным процессором MS Excel, математическим пакетом Mathcad и пакетом статистической обработки данных Statistica.
Этап вложения. Для экспериментальных исследований исходный ряд 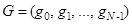 может быть задан по известным функциям либо определен результатами функционирования исследуемой системы. По известным функциям ряд формируется на рабочем листе MS Excel и затем в пакете Mathcad формируется матрица А, которая по правилам построения является ганкелевой [5]. Процедура вложения является преобразованием исходного одномерного ряда может быть задан по известным функциям либо определен результатами функционирования исследуемой системы. По известным функциям ряд формируется на рабочем листе MS Excel и затем в пакете Mathcad формируется матрица А, которая по правилам построения является ганкелевой [5]. Процедура вложения является преобразованием исходного одномерного ряда 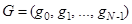 в последовательность в последовательность 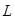 -мерных векторов, число которых равно -мерных векторов, число которых равно 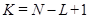 : :
 , , 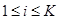 . (1) . (1)
Эти вектора образуют траекторную матрицу 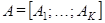 ряда ряда 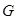 , в которой. , в которой.  , т. е. матрица , т. е. матрица 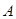 имеет одинаковые элементы на диагонали имеет одинаковые элементы на диагонали  . .
Этап сингулярного разложения. Обозначим 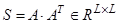 . Матрица . Матрица  симметричная и неотрицательно определенная, а значит ее собственные числа симметричная и неотрицательно определенная, а значит ее собственные числа  вещественны и неотрицательны. Представленные в виде вещественны и неотрицательны. Представленные в виде 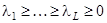 собственные числа называют сингулярными значениями матрицы А. Пусть собственные числа называют сингулярными значениями матрицы А. Пусть 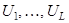 – соответствующие им ортонормированные собственные вектора. Будем называть – соответствующие им ортонормированные собственные вектора. Будем называть 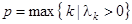 порядком сингулярного разложения. Обозначим порядком сингулярного разложения. Обозначим
 . (2) . (2)
Тогда сингулярным разложением матрицы A называется ее представление в виде суммы элементарных матриц
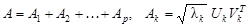 . (3) . (3)
Каждая из матриц 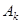 имеет ранг, равный единице. Поэтому их можно назвать элементарными матрицами. Вектор имеет ранг, равный единице. Поэтому их можно назвать элементарными матрицами. Вектор 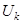 называют k-м левым сингулярным вектором или просто k-м собственным вектором, вектор называют k-м левым сингулярным вектором или просто k-м собственным вектором, вектор 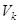 – правым сингулярным вектором. – правым сингулярным вектором.
Набор 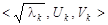 будем называть k-ой собственной тройкой. будем называть k-ой собственной тройкой.
Собственные числа  матрицы А в пакете Mathcad представлены вектором d. Вектор в сингулярных значений в Mathcad определяется с использованием функции svds() [6]: матрицы А в пакете Mathcad представлены вектором d. Вектор в сингулярных значений в Mathcad определяется с использованием функции svds() [6]:
d := svds(A). (4)
Диагональная матрица ds сингулярных значений матрицы А в пакете Mathcad определяется с использованием функции diag():
ds := diag(d). (5)
Объединенная матрица AS с левыми и правыми сингулярными векторами определяется с использованием функции svd ():
AS := svd(A). (6)
Для разделения левых и правых сингулярных векторов из матрицы AS используется функция submatrix() [6].
Этап группировки. Вид левых и правых сингулярных векторов, трактуемых в SSA как временные ряды, является очень важным для следующего шага метода – группировки [3]. При этом для одномерного SSA левые и правые сингулярные вектора обладают определенной симметрией, так как в этих случаях сингулярные разложения траекторных матриц с длиной окна  и и 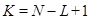 эквивалентны. эквивалентны.
Процедура группировки формально одинакова для всех разновидностей SSA. На основе разложения (3) процедура группировки делит все множество индексов  на на  непересекающихся подмножеств непересекающихся подмножеств 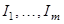 . .
Пусть 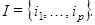 Тогда результирующая матрица Тогда результирующая матрица 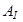 , соответствующая группе , соответствующая группе 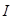 , определяется как , определяется как  .Такие матрицы вычисляются для .Такие матрицы вычисляются для 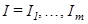 , тем самым разложение (3) может быть записано в сгруппированном виде: , тем самым разложение (3) может быть записано в сгруппированном виде:
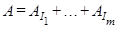 .(7) .(7)
Процедура выбора множеств  и называется группировкой собственных троек. Для определения и называется группировкой собственных троек. Для определения  в MS Excel используется лепестковая диаграмма, которая является аналогом графика в полярной системе координат, отображая распределение значений относительно начала координат. По особенностям представления сингулярных векторов на лепестковой диаграмме принимается решение о принадлежности их одной группе. в MS Excel используется лепестковая диаграмма, которая является аналогом графика в полярной системе координат, отображая распределение значений относительно начала координат. По особенностям представления сингулярных векторов на лепестковой диаграмме принимается решение о принадлежности их одной группе.
Этап диагонального усреднения. На последнем шаге базового алгоритма каждая матрица сгруппированного разложения переводится в новый ряд длины 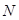 . Для произвольной матрицы X процедуру приведения ее к ганкелевому виду и последующему преобразованию в ряд (обозначим его как Gв
) выразим следующим образом. Пусть . Для произвольной матрицы X процедуру приведения ее к ганкелевому виду и последующему преобразованию в ряд (обозначим его как Gв
) выразим следующим образом. Пусть 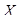 – матрица размера – матрица размера 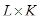 с элементами с элементами  , ,  , ,  . Положим . Положим 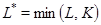 , , 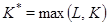 и и 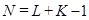 . Пусть . Пусть 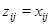 , если , если 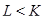 и и  в остальных случаях. Тогда диагональное усреднение переводит матрицу в остальных случаях. Тогда диагональное усреднение переводит матрицу 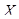 в ряд в ряд  по формуле по формуле
 (8) (8)
Это выражение соответствует усреднению элементов матрицы вдоль побочных диагоналей  : выбор : выбор 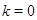 дает дает  , для , для 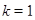 получаем получаем 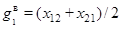 и т. д. Применив диагональное усреднение к матрицам, полученным на этапе группировки, приходим к разложению исходного ряда в сумму и т. д. Применив диагональное усреднение к матрицам, полученным на этапе группировки, приходим к разложению исходного ряда в сумму 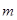 рядов. рядов.
Процедуру диагонального усреднения просто и наглядно предложено выполнить в MS Excel. Для этого матрица, подлежащая диагонализации, размещается на рабочем листе. Затем блок матрицы, следующий за первой строкой сдвигается вправо на одну позицию. В сдвинутом блоке также определяется блок, следующий за первой строкой, который сдвигается вправо на одну позицию. Процедура повторяется до тех пор, пока в очередном блоке не останется ни одной строки. Восстановленный ряд Gв
определяется аналогично формуле (1) с использованием функции СРЗНАЧ() в MS Excel. Затем исследуется в пакете Statistica.
4. Исследование временных рядов с шумом заданным Pearson Type V законом распределения
4.1 Постановка эксперимента
Для проведения исследований выбрана функция 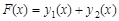 +rnd, где +rnd, где 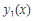 – линейная функция, y1(x)= 0.1+0.09x; – линейная функция, y1(x)= 0.1+0.09x;  – гармоническая функция, y2(x)=3sin(x); rnd – шум. Переменная – гармоническая функция, y2(x)=3sin(x); rnd – шум. Переменная  принимает значения от 0 до 42 с шагом, равным единице. Таким образом, длина N ряда принимает значения от 0 до 42 с шагом, равным единице. Таким образом, длина N ряда 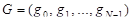 , равна 43. При этом длина окна , равна 43. При этом длина окна 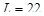 , число L-мерных векторов , число L-мерных векторов 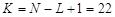 . Отдельно на рабочем листе MS Excel 2003 рассчитаны значения функций . Отдельно на рабочем листе MS Excel 2003 рассчитаны значения функций 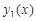 , , , rnd и , rnd и 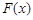 . При этом ряду . При этом ряду  линейной функции, или тренда, соответствуют значения Gy1={gy10,gy11,…,gy142}={ 0.1, 0.19,..,3.88}. Ряд линейной функции, или тренда, соответствуют значения Gy1={gy10,gy11,…,gy142}={ 0.1, 0.19,..,3.88}. Ряд 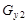 гармонической составляющей – Gy2={gy20,gy21,…,gy242}={ 0, 2.524,..,-2.749}, Rnd={1.489, 0.155,..,0.65} и G={1.59, 2.87,..,1.78}. Элементы ряда гармонической составляющей – Gy2={gy20,gy21,…,gy242}={ 0, 2.524,..,-2.749}, Rnd={1.489, 0.155,..,0.65} и G={1.59, 2.87,..,1.78}. Элементы ряда  копируются в траекторную матрицу A на рабочем листе Mathcad 14.0. копируются в траекторную матрицу A на рабочем листе Mathcad 14.0.
Сформированная матрица A является ганкелевой размером 22×22. Следует отметить, что размеры матрицы при ручном вводе ограничены возможностями Mathcad и не должны превышать 600 позиций. Сингулярные числа при сингулярном разложении траекторной матрицы A с применением функции svds() по формуле (4) принимают следующие значения: λ1= 92.196; λ2=33.886; λ3=33.794. Остальные значения λ4,…,λ22 представляют убывающую последовательность: 19.575,…, 1.732.
Сингулярное разложение в пакете Mathcad 14.0 реализуется с помощью функции svd() по формуле (6), формируется обобщенная матрица AS, включающая левые и правые сингулярные вектора. Левые и правые сингулярные вектора разделяются по формулам  и и  соответственно. соответственно.
Диагональная матрица ds сингулярных чисел определена по формуле (5). Для контроля правильности выполненных вычислений определяется равенство
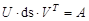 . (9) . (9)
Для последующих расчетов определяются скалярные значения собственных чисел по формулам с использованием функции submatrix(). Например, для 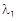 (обозначение ds0 в пакете Mathcad) (обозначение ds0 в пакете Mathcad)
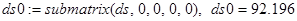 , (10) , (10)
для 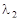 (обозначение ds1 в пакете Mathcad) (обозначение ds1 в пакете Mathcad)
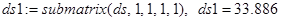 и т. д. (11) и т. д. (11)
Левые сингулярные вектора определяются из матрицы U аналогично с использованием функции submatrix():
 , (12) , (12)
 и т. д. (13) и т. д. (13)
Правые сингулярные вектора определяются в пакете Mathcad по формуле
 . (14) . (14)
Элементарные матрицы Xi
определены по формуле
 . (15) . (15)
Таблица 4.1 – Исходные данные для исследования временного ряда
| Составляющие исходного ряда F(x)j
|
Потенциалы составляющих исходного ряда
|
| F(x)j
|
Тренд ax + b
|
Гармоника с·sinx
|
Шум rnd
|
φT
|
φS
|
φN
|
| F(x)0
|
0.1+0.09x
|
3sin(x)
|
rnd
|
85.57
|
81.44938204
|
86.94553
|
| F(x)1
|
0.1+0.09x
|
3sin(x)
|
10rnd
|
85.57
|
81.44938204
|
869.4553
|
| F(x)2
|
0.1+0.09x
|
30sin(x)
|
rnd
|
85.57
|
814.4938204
|
86.94553
|
| F(x)3
|
0.1+0.09x
|
30sin(x)
|
10rnd
|
85.57
|
814.4938204
|
869.4553
|
| F(x)4
|
10(0.1+0.09x)
|
3sin(x)
|
rnd
|
855.7
|
81.44938204
|
86.94553
|
| F(x)5
|
10(0.1+0.09x)
|
3sin(x)
|
10rnd
|
855.7
|
81.44938204
|
869.4553
|
| F(x)6
|
10(0.1+0.09x)
|
30sin(x)
|
rnd
|
855.7
|
814.4938204
|
86.94553
|
| F(x)7
|
10(0.1+0.09x)
|
30sin(x)
|
10rnd
|
855.7
|
814.4938204
|
869.4553
|
Таблица 4.2 – Собственные числа при сингулярном спектральном анализе временных рядов F(x)j
| λi
|
F(x)0
|
F(x)1
|
F(x)2
|
F(x)3
|
F(x)4
|
F(x)5
|
F(x)6
|
F(x)7
|
| λ1
λ2
λ3
λ4
λ5
λ6
λ7
λ8
λ9
λ10
λ11
λ12
λ13
λ14
λ15
λ16
λ17
λ18
λ19
λ20
λ21
λ22
|
92.196
33.886
33.794
19.575
15.968
14.193
13.288
12.5
11.969
10.978
10.875
10.004
9.718
8.824
8.702
7.372
6.554
6.406
5.958
1.974
1.894
1.732
|
515.747
195.792
160.277
143.162
132.928
125.87
123.748
114.367
111.448
109.846
107.852
100.137
97.35
86.226
81.9
74.488
67.182
63.022
61.566
21.719
18.66
13.31
|
331.554
328.913
89.658
19.577
15.956
14.173
13.29
12.512
11.932
10.976
10.885
9.997
9.739
8.82
8.736
7.31
6.483
6.394
5.876
2.117
2.021
1.751
|
525.525
337.9
335.737
195.704
159.631
141.406
132.878
124.274
119.619
109.785
108.358
99.928
97.352
88.46
83.315
73.455
65.653
63.705
59.799
19.779
18.947
17.205
|
513.814
35.083
34.027
33.055
19.459
15.963
13.826
13.273
12.46
11.955
10.963
10.707
9.988
9.687
8.691
7.509
6.595
6.452
5.598
3.433
1.84
1.81
|
915.716
195.886
160.303
143.794
132.949
126.517
123.756
114.365
111.423
109.833
108.326
100.173
97.316
86.543
86.049
74.529
66.855
63.198
61.422
21.692
18.624
13.185
|
525.945
328.695
316.756
34.273
19.463
15.952
13.819
13.275
12.467
11.916
10.962
10.716
9.98
9.702
8.706
7.441
6.627
6.421
5.507
3.711
1.887
1.82
|
921.985
338.831
337.916
195.808
159.66
141.892
132.892
125.017
119.647
109.769
108.785
99.985
97.209
88.221
87.083
73.675
65.529
64.064
59.584
19.762
18.949
17.304
|
4.2 Экспериментальная часть (тренд)
Для определения групп элементарных матриц Xi
построены лепестковые диаграммы для векторов Vi
в табличном процессоре MS Excel 2003 (рисунок 4.1).
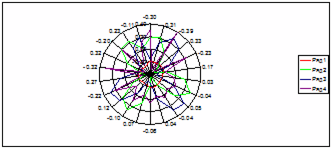
Рисунок 4.1 Лепестковая диаграмма
Где ряд 1 - тренд, ряд 2 и ряд 3 - гармоники, ряд 4-22 – шум.
Тогда группа X1 элементарных матриц соответствует тренду ряда: 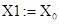 . Группа . Группа 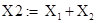 соответствует гармонической составляющей ряда. Группа соответствует гармонической составляющей ряда. Группа 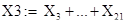 соответствует шумовой составляющей ряда. соответствует шумовой составляющей ряда.
| 
|
|
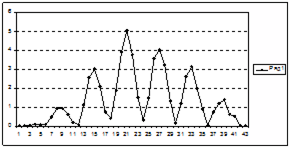
| Рисунок 4.2 – Распределение абсолютной ошибки восстановления
трендовой составляющей
|
Рисунок 4.3 – Распределение суммы квадратов отклонений трендовой
составляющей
|
4.3 Экспериментальная часть (гармонический ряд)
Группа X2 включает в себя все  вошедшие в гармоническую составляющую: вошедшие в гармоническую составляющую:
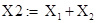
| 
|
|
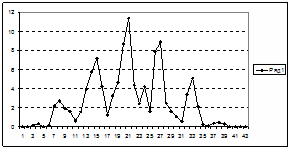
| Рисунок 4.4 – Распределение абсолютной ошибки восстановления гармонической составляющей
|
Рисунок 4.5 – Распределение суммы квадратов отклонений гармонической составляющей
|
4.4 Экспериментальная часть (рандом)
Группа X3 включает в себя все  не вошедшие ни в тренд, ни в гармоническую составляющую: не вошедшие ни в тренд, ни в гармоническую составляющую:

| 
|

|
| Рисунок 4.6 – Распределение абсолютной ошибки восстановления “шумовой” составляющей
|
Рисунок 4.7 – Распределение суммы квадратов отклонений “шумовой” составляющей
|
4.5 Результаты и их обсуждение
В ходе проведенных исследований временных детерминированных рядов, образованных функциями вида F(x) = ax + bsinx + c, построена таблица 4.3.
Таблица 4.3. – Результаты исследования временных рядов
| Временной ряд, заданный функцией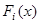
|
Трендовая составляющая
|
Гармоническая составляющая
|
| Vтренд
|
Vгарм
|
| 1) y=0.1+0.09x+3*sin(x)+rnd
|
V0
|
-
|
V1
|
V2
|
-
|
| 2) y=0.1+0.09x+3*sin(x)+10rnd
|
V0
|
-
|
-
|
-
|
-
|
| 3) y=0.1+0.09x+30*sin(x)+rnd
|
-
|
-
|
V0
|
V1
|
V2
|
| 4) y=0.1+0.09x+30*sin(x)+10rnd
|
-
|
-
|
V0
|
V1
|
V2
|
| 5)y=10(0.1+0.09x)+3*sin(x)+rnd
|
V0
|
-
|
V1
|
V2
|
V3
|
| 6)y=10(0.1+0.09x)+3*sin(x)+10rnd
|
V0
|
-
|
-
|
-
|
-
|
| 7)y=10(0.1+0.09x)+30*sin(x)+rnd
|
V3
|
-
|
V0
|
V1
|
V2
|
| 8)y=10(0.1+0.09x)+30*sin(x)+10rnd
|
V0
|
-
|
V1
|
V2
|
-
|
Особенность группировки составляющих ряда определяется перестановками сингулярных векторов, ответственных за трендовую и гармоническую составляющую.
5. Исследование временных рядов с шумом заданным Rayleigh законом распределения
5.1 Постановка эксперимента
Для проведения исследований выбрана функция 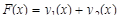 +rnd, где +rnd, где  – линейная функция, y1(x)=0.1+0.055x; – линейная функция, y1(x)=0.1+0.055x; 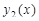 – гармоническая функция, y2(x)=2sin(x); rnd – шум. Переменная – гармоническая функция, y2(x)=2sin(x); rnd – шум. Переменная  принимает значения от 0 до 42 с шагом, равным единице. Таким образом, длина N ряда принимает значения от 0 до 42 с шагом, равным единице. Таким образом, длина N ряда 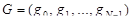 , равна 43. При этом длина окна , равна 43. При этом длина окна 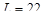 , число L-мерных векторов , число L-мерных векторов 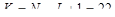 . Отдельно на рабочем листе MS Excel 2003 рассчитаны значения функций . Отдельно на рабочем листе MS Excel 2003 рассчитаны значения функций 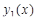 , ,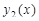 , rnd и , rnd и  . При этом ряду . При этом ряду  линейной функции, или тренда, соответствуют значения Gy1={gy10,gy11,…,gy142}={ 0.1, 0.155,..,2.41}. Ряд линейной функции, или тренда, соответствуют значения Gy1={gy10,gy11,…,gy142}={ 0.1, 0.155,..,2.41}. Ряд 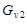 гармонической составляющей – Gy2={gy20,gy21,…,gy242}={ 0, 1.68,..,-1.83}, Rnd={1.84, 2.87,..,0.827} и G={1.94, 4.71,..,1.4}. Элементы ряда гармонической составляющей – Gy2={gy20,gy21,…,gy242}={ 0, 1.68,..,-1.83}, Rnd={1.84, 2.87,..,0.827} и G={1.94, 4.71,..,1.4}. Элементы ряда  копируются в траекторную матрицу A на рабочем листе Mathcad 14.0. Сформированная матрица A является ганкелевой размером 22×22. Следует отметить, что размеры матрицы при ручном вводе ограничены возможностями Mathcad и не должны превышать 600 позиций. Сингулярные числа при сингулярном разложении траекторной матрицы A с применением функции svds() по формуле (4) принимают следующие значения: λ1=58.997; λ2=24.184; λ3=23.729. Остальные значения λ4,…,λ22 представляют убывающую последовательность: 5.404,…,0.228. копируются в траекторную матрицу A на рабочем листе Mathcad 14.0. Сформированная матрица A является ганкелевой размером 22×22. Следует отметить, что размеры матрицы при ручном вводе ограничены возможностями Mathcad и не должны превышать 600 позиций. Сингулярные числа при сингулярном разложении траекторной матрицы A с применением функции svds() по формуле (4) принимают следующие значения: λ1=58.997; λ2=24.184; λ3=23.729. Остальные значения λ4,…,λ22 представляют убывающую последовательность: 5.404,…,0.228.
Сингулярное разложение в пакете Mathcad 14.0 реализуется с помощью функции svd() по формуле (6), формируется обобщенная матрица AS, включающая левые и правые сингулярные вектора. Левые и правые сингулярные вектора разделяются по формулам 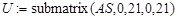 и и  соответственно. соответственно.
Диагональная матрица ds сингулярных чисел определена по формуле (5). Для контроля правильности выполненных вычислений определяется равенство
 . (9) . (9)
Для последующих расчетов определяются скалярные значения собственных чисел по формулам с использованием функции submatrix(). Например, для 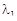 (обозначение ds0 в пакете Mathcad) (обозначение ds0 в пакете Mathcad)
 , (10) , (10)
для 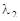 (обозначение ds1 в пакете Mathcad) (обозначение ds1 в пакете Mathcad)
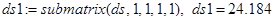 и т. д. (11) и т. д. (11)
Левые сингулярные вектора определяются из матрицы U аналогично с использованием функции submatrix():
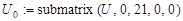 , (12) , (12)
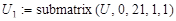 и т. д. (13) и т. д. (13)
Правые сингулярные вектора определяются в пакете Mathcad по формуле
 . (14) . (14)
Элементарные матрицы Xi
определены по формуле
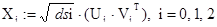 . (15) . (15)
Таблица 5.1 – Исходные данные для исследования временного ряда
| Составляющие исходного ряда F(x)j
|
Потенциалы составляющих исходного ряда
|
|
F
(x)j
|
Тренд ax + b
|
Гармоника с·sinx
|
Шум rnd
|
φT
|
φS
|
φN
|
| F(x)0
|
0.1+0.055x
|
2sin(x)
|
rnd
|
53.965
|
54.29958803
|
55.72192
|
| F(x)1
|
0.1+0.055x
|
2sin(x)
|
10rnd
|
53.965
|
54.29958803
|
557.2192
|
| F(x)2
|
0.1+0.055x
|
20sin(x)
|
rnd
|
53.965
|
542.9958803
|
55.72192
|
| F(x)3
|
0.1+0.055x
|
20sin(x)
|
10rnd
|
53.965
|
542.9958803
|
557.2192
|
| F(x)4
|
10(0.1+0.055x)
|
2sin(x)
|
rnd
|
539.65
|
54.29958803
|
55.72192
|
| F(x)5
|
10(0.1+0.055x)
|
2sin(x)
|
10rnd
|
539.65
|
54.29958803
|
557.2192
|
| F(x)6
|
10(0.1+0.055x)
|
20sin(x)
|
rnd
|
539.65
|
542.9958803
|
55.72192
|
| F(x)7
|
10(0.1+0.055x)
|
20sin(x)
|
10rnd
|
539.65
|
542.9958803
|
557.2192
|
Таблица 5.2 – Собственные числа при сингулярном спектральном анализе временных рядов F(x)j
| λi
|
F(x)0
|
F(x)1
|
F(x)2
|
F(x)3
|
F(x)4
|
F(x)5
|
F(x)6
|
F(x)7
|
| λ1
λ2
λ3
λ4
λ5
λ6
λ7
λ8
λ9
λ10
λ11
λ12
λ13
λ14
λ15
λ16
λ17
λ18
λ19
λ20
λ21
λ22
|
58.997
24.184
23.729
5.404
5.331
4.454
4.112
4.01
3.807
3.768
3.482
3.422
3.086
2.903
2.373
2.24
1.895
1.859
1.566
1.499
1.361
0.228
|
330.15
54.463
53.732
46.596
46.365
43.26
40.101
38.279
37.603
35.482
34.728
34.278
29.542
28.412
23.721
22.454
18.883
18.838
15.537
15.097
13.484
2.384
|
223.425
222.2
57.172
5.416
5.35
4.443
4.102
4.01
3.798
3.757
3.488
3.426
3.089
2.909
2.382
2.24
1.877
1.858
1.56
1.494
1.357
0.25
|
341.176
241.956
231.45
54.212
53.4
44.113
40.123
38.356
37.702
35.491
34.692
34.329
30.376
29.281
23.91
22.49
18.965
18.889
15.569
15.08
13.554
2.392
|
324.008
24.177
23.928
20.601
5.364
5.315
4.408
4
3.821
3.721
3.501
3.415
3.116
2.83
2.395
2.245
1.922
1.891
1.553
1.508
1.358
0.226
|
584.944
54.45
53.799
46.612
46.361
43.463
41.141
40.081
37.987
37.556
34.953
34.267
29.906
28.273
23.596
22.454
18.847
18.601
15.643
15.088
13.586
2.354
|
333.228
222.05
212.455
20.592
5.378
5.335
4.408
4.009
3.819
3.707
3.498
3.408
3.118
2.839
2.407
2.253
1.93
1.896
1.563
1.504
1.361
0.244
|
590.12
241.876
237.353
54.179
53.45
44.394
41.084
40.101
37.999
37.62
34.924
34.289
30.824
29.121
23.802
22.481
18.879
18.641
15.694
15.082
13.672
2.364
|
5.2 Экспериментальная часть (тренд)
Для определения групп элементарных матриц Xi
построены лепестковые диаграммы для векторов Vi
в табличном процессоре MS Excel 2003 (рисунок 5.1).
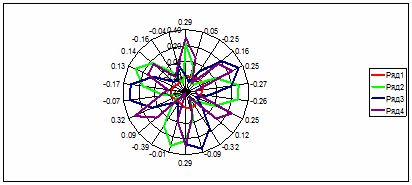
Рисунок 5.1 Лепестковая диаграмма
Где ряд 1 - тренд, ряд 2 и ряд 3 - гармоники, ряд 4-22 – шум.
Тогда группа X1 элементарных матриц соответствует тренду ряда: 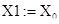 . Группа . Группа 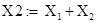 соответствует гармонической составляющей ряда. Группа соответствует гармонической составляющей ряда. Группа 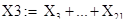 соответствует шумовой составляющей ряда. соответствует шумовой составляющей ряда.
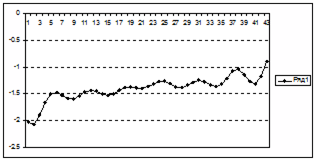
| 
|

|
| Рисунок 5.2 – Распределение абсолютной ошибки восстановления трендовой составляющей
|
Рисунок 5.3 – Распределение суммы квадратов отклонений трендовой составляющей
|
5.3 Экспериментальная часть (гармонический ряд)
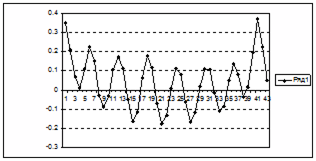
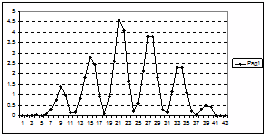
Группа X2 включает в себя все 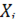 вошедшие в гармоническую составляющую: вошедшие в гармоническую составляющую:

| 
|
|
| Рисунок 5.4 – Распределение абсолютной ошибки восстановления гармонической составляющей
|
Рисунок 5.5 – Распределение суммы квадратов отклонений гармонической составляющей
|
5.4 Экспериментальная часть (рандом)
Группа X3 включает в себя все 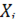 не вошедшие ни в тренд, ни в гармоническую составляющую: не вошедшие ни в тренд, ни в гармоническую составляющую:
| 
|

|
| Рисунок 5.6 – Распределение абсолютной ошибки восстановления “шумовой” составляющей
|
Рисунок 5.7 – Распределение суммы квадратов отклонений “шумовой” составляющей
|
5.5 Результаты и их обсуждение
В ходе проведенных исследований временных детерминированных рядов, образованных функциями вида F(x) = ax + bsinx + c, построена таблица 5.3.
Таблица 5.3. – Результаты исследования временных рядов
| Временной ряд, заданный функцией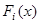
|
Трендовая составляющая
|
Гармоническая составляющая
|
| Vтренд
|
Vгарм
|
| 1)y=0.1+0.055x+2sin(x)+rnd
|
V0
|
-
|
V1
|
V2
|
-
|
| 2)y=0.1+0.055x+2sin(x)+10rnd
|
V0
|
-
|
-
|
-
|
-
|
| 3)y=0.1+0.055x+20sin(x)+rnd
|
V2
|
-
|
V0
|
V1
|
-
|
| 4)y=0.1+0.055x+20sin(x)+10rnd
|
-
|
-
|
V0
|
V1
|
V2
|
| 5)y=10(0.1+0.055x)+2sin(x)+rnd
|
V0
|
V3
|
V1
|
V2
|
-
|
| 6)y=10(0.1+0.055x)+2sin(x)+10rnd
|
V0
|
-
|
-
|
-
|
-
|
| 7)y=10(0.1+0.055x)+20sin(x)+rnd
|
V0
|
V3
|
V1
|
V2
|
-
|
| 8)y=10(0.1+0.055x)+20sin(x)+10rnd
|
V0
|
-
|
V1
|
V2
|
-
|
Особенность группировки составляющих ряда определяется перестановками сингулярных векторов, ответственных за трендовую и гармоническую составляющую.
6. Э
кспериментальное исследование средней трудоемкости алгоритма для генерации случайных чисел по закону Pirson
Type V
Трудоёмкость алгоритма генерации случайного числа зависит от 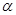 , ,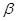 , ,
где 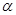 -параметр формы (α > 0), -параметр формы (α > 0), 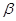 - масштабный параметр (β > 0). - масштабный параметр (β > 0).

Рисунок 6.1 - График зависимости средней трудоёмкости от α (при β=1) для алгоритма генерации случайного числа по закону Pirson Type V
7. Э
кспериментальное исследование средней трудоемкости алгоритма для генерации случайных чисел по закону
Rayleigh
Трудоёмкость алгоритма генерации случайного числа зависит от a,
где a – параметр масштаба (а>0)

Рисунок 7.1 - Графики зависимости трудоёмкости от a и выборки

Рисунок 7.2 - График зависимости средней трудоёмкости от a для алгоритма генерации случайного числа по закону Rayleigh
Заключение
Факты, обнаруженные при исследовании.
1)Гармоническая составляющая по закону распределения Rayleigh восстанавливается со средним значением, близким к нулю. Например, для ряда F(x)0
среднее значение восстановленной составляющей равно -0.00823, а для исходной составляющей 0.038. (см. рисунок 6.1)

Рисунок 6.1. - Среднее значение восстановленной и исходной составляющей
2)Составляющая шума по закону распределения Rayleigh восстанавливается со средним значением, близким к нулю. Для ряда F(x)0
среднее значение восстановленной составляющей равно -0,0605, а для исходной составляющей 1,29.
3)Постоянная составляющая шума исключается при восстановлении и суммируется с линейной составляющей исходного ряда.
4)Значения восстановленных случайных чисел принадлежат исходному интервалу (с учетом исключения постоянной составляющей) с небольшой погрешностью. Например, для ряда F(x)0
исходные случайные числа принадлежат интервалу (0,01; 3,14), восстановленные случайные числа принадлежат интервалу (– 1,1; 1,6).
Методика применения полученных результатов состоит в построении имитационной модели объекта в соответствии с технологиями, представленными выше.
Список использованных источников
1. Айвазян, С. А. Прикладная статистика. Основы моделирования и первичная обработка данных : справоч. изд. / С. А. Айвазян, И. С. Енюков, Л. Д. Мешалкин. – М.: Финансы и статистика, 1983. – 471 с.
2. Крамер, Г. Математические методы статистики : пер. с англ. / Г. Крамер. – 2-е изд. – М.: Мир, 1975. – 648 с.
3. Большев, Л. Н. Таблицы математической статистики / Л. Н. Большев, Н. В. Смирнов. – М.: Наука, 1983. – 416 с.
4. Рунион, Р. Справочник по непараметрической статистике. Современный подход : пер. с англ. / Р. Рунион. – М. Финансы и статистика, 1982. – 198 с.
5. Муха, В. С. Статистические методы обработки данных : учеб. пособие / В. С. Муха.
–
Минск: Изд. центр БГУ, 2009. – 183 с.
6. Hyndman, R. J. The problem with Sturges’ rule for constructing histograms [Электрон
. ресурс] / R. J. Hyndman. – 1995. – Режим доступа : http: // www.robjhyndman.com / papers / sturges.pdf. – Дата доступа : 12.04.2010.
7. Таран, Т. А. Искусственный интеллект. Теория и приложения : учеб. пособие / Т.
А. Таран, Д. А. Зубов. – Луганск: ВНУ им. В. Даля, 2006. – 240 с.: ил.
8. Якимов, Е. А. Интеллектуальный анализ входных данных при эксплуатации имитационной модели / Е.
А. Якимов; науч. рук.: И. В. Максимей // Новые материалы, оборудование и технологии в промышленности : материалы междунар. науч.-техн. конф. молод. ученых, Могилев, 19-20 ноября 2009 г. – Могилев: Белорус.-Рос. ун-т, 2009. – С. 121.
9. Голяндина, Н.Э. Метод «Гусеница»-
SSA: анализ временных рядов: Учебное пособие / Н.Э. Голяндина. – СПб.: С.-Петерб. гос. ун-т, 2004. – 76 с.
10. Голуб, Дж. Матричные вычисления: пер. с англ. /
Дж. Голуб, Ч. Ван Лоун. – М.: Наука, 1999. – 548 с.: ил.
11. Гантмахер, Ф.Р. Теория матриц / Ф.Р.
Гантмахер; 2-е изд., доп. – М.: Наука, 1966. – 576 с.: ил.
12. Ивановский, Р.И. Компьютерные технологии в науке и образовании. Практика применения систем
MathCAD Pro: учеб. пособие / Р.И. Ивановский. – М.: Высш. шк., 2003. – 431 с.: ил.
13. Якимов, Е.А. Исследование SSA-метода на основе комплексного применения информационных технологий / Е. А. Якимов // Доклады БГУИР. – 2010. – № 2(48). – С. 77–83.
14. Якимов, Е.А. Исследование детерминированных временных последовательностей данных на основе SSA-метода / Е. А. Якимов, И. В. Максимей
// Информационные технологии, энергетика и экономика (информационные технологии, математическое моделирование технологических процессов, электроника): сб. трудов 7-ой Межрег. (межд.) науч.-техн. конф. студентов и аспирантов, 8–9 апр. 2010 г. : в 3 т. – Смоленск: ф-л ГОУ ВПО МЭИ(ТУ), 2010. – Т. 2. – С. 103–107.
|