Содержание
Введение
Глава 1. Основные понятия теории рядов
1.1 Определения и термины
1.2 Истоки проблемы
Глава 2. Метод степенных рядов
2.1 Суть метода
2.2 Теорема Абеля
2.3 Теорема Таубера
Глава 3. Метод средних арифметических
3.1 Суть метода
3.2 Взаимоотношение между методами Пуассона-Абеля и Чезаро
3.3 Теорема Харди-Ландау
3.4 Применение обобщенного суммирования к умножению рядов
Глава 4. Другие методы обобщенного суммирования
4.1 Методы Г.Ф. Вороного
4.2 Обобщенные методы Чезаро
4.3 Метод Бореля
4.4 Метод Эйлера
Заключение
Список использованной литературы
Как мы уже знаем математический анализ, занимается проблемами изучения множества объектов, таких как: числа, переменные, функции, последовательности, ряды и др. При изучении свойств того или иного объекта могут возникать пробелы или “пустоты". Это возникает тогда, когда наука не может объяснить: “Почему происходит так, а не иначе? ”. Такой казус существовал некоторое время и при изучении рядов, а точнее при изучении расходящихся рядов
.
При изучении рядов заданному числовому ряду
 (А) (А)
в качестве его суммы мы приписывали предел её частичной суммы  , в предположении, что этот предел существует и конечен. “Колеблющийся" расходящийся ряд оказывался лишенным суммы и подобные ряды, как правило, из рассмотрения исключали. Естественно возникает вопрос о возможности суммирования расходящихся рядов
в некоем новом смысле, конечно отличном от обычного. Этот вопрос возник ещё до второй половины XIX века. Некоторые методы такого суммирования оказались довольно-таки плодотворными. , в предположении, что этот предел существует и конечен. “Колеблющийся" расходящийся ряд оказывался лишенным суммы и подобные ряды, как правило, из рассмотрения исключали. Естественно возникает вопрос о возможности суммирования расходящихся рядов
в некоем новом смысле, конечно отличном от обычного. Этот вопрос возник ещё до второй половины XIX века. Некоторые методы такого суммирования оказались довольно-таки плодотворными.
В данной своей работе я хочу рассмотреть эти методы, обратить внимание на то, где и какой метод наиболее применим, изучить связь между этими методами. Моя работа состоит из 4 глав, первая из которых содержит основные термины и определения необходимые для работы. Последующие главы рассматривают непосредственно сами методы суммирования. Вторая и третья главы посвящены двум основным методам суммирования: метод степенных рядов
и метод средних арифметических
, а третья содержит сведения о других существующих, но реже применяемых методах. Каждая из четырех глав содержит примеры суммирования рядов по данному конкретному методу.
Как мы упомянули вначале цель нашего исследования - расходящиеся ряды
. А что же такое, вообще, ряд
?
Пусть задана некоторая бесконечная последовательность чисел
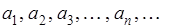 (1) (1)
Составленный из этих чисел символ
 (2) (2)
называется бесконечным рядом
, а сами числа (1) - членами ряда. Вместо (2), пользуясь знаком суммы, часто пишут так:
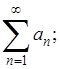 (2а) (2а)
Станем последовательно складывать члены ряда, составляя (в бесконечном количестве) суммы;
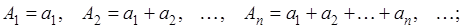 (3) (3)
их называют частичными суммами ряда.
Конечный или бесконечный предел А частичной суммы  ряда (
2) при ряда (
2) при 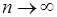 : : 
называют суммой ряда
и пишут
 , ,
Придавая тем самым символу (2) или (2а) числовой смысл. Если ряд имеет конечную сумму, его называют сходящимся, в противном же случае (т. е если сумма равна
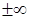 , либо же суммы вовсе нет) - расходящимся. , либо же суммы вовсе нет) - расходящимся.
Примеры.1) простейшим примером бесконечного ряда является уже знакомая геометрическая прогрессия:
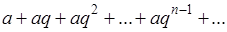
Его частичная сума будет (если  ) )
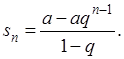
Если знаменатель прогрессии, q, по абсолютной величине меньше единицы, то 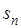 имеет конечный предел имеет конечный предел
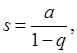
то есть наш ряд сходится, и  будет его суммой. будет его суммой.
При  та же прогрессия дает пример расходящегося ряда. Если та же прогрессия дает пример расходящегося ряда. Если  , то его суммой будет бесконечность (определенного знака), в прочих случаях суммы вовсе нет. Отметим, в частности, любопытный ряд, который получается при a=1
и q= - 1; , то его суммой будет бесконечность (определенного знака), в прочих случаях суммы вовсе нет. Отметим, в частности, любопытный ряд, который получается при a=1
и q= - 1;
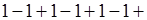 … … 1+ (-1) +1+ (-1) +1+… 1+ (-1) +1+ (-1) +1+…
Его частичные суммы попеременно равны то 1, то 0.
2) Легко установить расходимость ряда
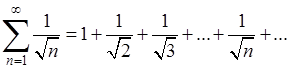
В самом деле, так как члены его убывают, то его n
-я частичная сумма
 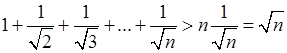
и растет до бесконечности вместе с n.
Различные факты из области математического анализа, как, например, расходимость, произведения двух сходящихся рядов, естественно выдвинули вышеупомянутый вопрос: “О возможности суммирования расходящихся рядов, в некоем новом смысле”.
Нужно сказать, что до создания Коши строгой теории пределов (и связанной с нею теории рядов) расходящиеся ряды нередко встречались в математической практике.
Хотя применение их при доказательствах и оспаривалось, тем не менее иной раз делались попытки придавать им даже числовой смысл.
Вспомним, опять, наш колеблющийся ряд

Еще со времен Лейбница в качестве "суммы" приписывалось число 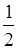 . Эйлер, например, мотивировал это тем, что из разложения . Эйлер, например, мотивировал это тем, что из разложения
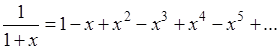
(которое в действительности имеет место лишь для 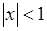 ) при подстановке вместо х
единицы как раз и получается ) при подстановке вместо х
единицы как раз и получается
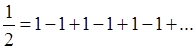
В этом уже содержалось зерно истины, но постановке вопроса не хватало четкости; самый произвол в выборе разложения оставлял открытой возможность, скажем из другого разложения (где п
и т -
любые, но 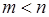 ) )
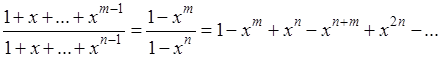
получить одновременно

Современный анализ ставит вопрос по-другому. В основу кладется то или иное точно сформулированное определение “обобщенной суммы" ряда, не придуманное только для конкретно интересующего нас числового ряда, но приложимое к целому ряду классов таких рядов. Определение “обобщенной суммы" обычно подчиняется двум требованиям.
Во-первых, если ряду
 приписывается
“обобщенная сумма" А, а ряду приписывается
“обобщенная сумма" А, а ряду  - “обобщенная сумма" В, то ряд - “обобщенная сумма" В, то ряд 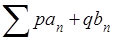 , где
p,
q- две произвольные постоянные, то должен иметь в качестве “обобщенной суммы" число , где
p,
q- две произвольные постоянные, то должен иметь в качестве “обобщенной суммы" число 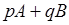 .
Метод суммирования, удовлетворяющий этому требованию, называется линейным. .
Метод суммирования, удовлетворяющий этому требованию, называется линейным.
Во-вторых, новое определение должно содержать обычное определение как частный случай. Точнее говоря, ряд, сходящийся в обычном смысле к сумме А, должен иметь “обобщенную сумму", и притом также равную А.
Метод суммирования, обладающий этим свойством, называют регулярным.
Разумеется, интерес представляют лишь такие регулярные методы, которые позволяют устанавливать “сумму” в более широком классе случаев, нежели обычный метод суммирования: лишь тогда с полным правом можно говорить об “обобщенном суммировании”. Мы переходим к теперь непосредственно к рассмотрению особо важных с точки зрения приложений методов ‘обобщенного суммирования".
Этот метод, в существенном принадлежит Пуассону, который сделал первую попытку применить его к тригонометрическим рядам. Он состоит в следующем.
По данному числовому ряду (А) строится степенной ряд
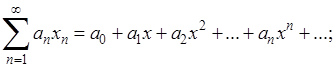 (
1) (
1)
Если этот ряд для 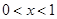 сходится и его сумма сходится и его сумма 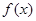 при при  имеет предел А: имеет предел А:
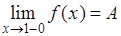 , ,
то число А и называют “обобщённой (в смысле Пуассона) суммой” данного ряда.
Примеры.1) Ряд, рассмотренный Эйлером:
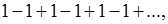
Здесь уже в силу самого определения приводит к степенному ряду, сумма которого  при при  стремится к пределу стремится к пределу 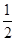 . Значит, число . Значит, число 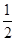 , действительно, является “обобщенной суммой” указанного в точном установленном здесь смысле. , действительно, является “обобщенной суммой” указанного в точном установленном здесь смысле.
2) Возьмем более общий пример: тригонометрический ряд
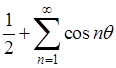 (2) (2)
является расходящимся при всех значениях 
Действительно, если 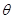 имеет вид имеет вид 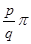 , где , где 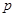 и и 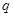 - натуральные числа, то для значений - натуральные числа, то для значений  , кратных , кратных 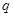 , будет , будет  , так что нарушено необходимое условие сходимости ряда. Если же отношение , так что нарушено необходимое условие сходимости ряда. Если же отношение  иррационально, то, разлагая его в бесконечную непрерывную дробь и составляя подходящие дроби иррационально, то, разлагая его в бесконечную непрерывную дробь и составляя подходящие дроби 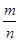 , будем иметь, как известно, , будем иметь, как известно,
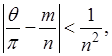 откуда откуда 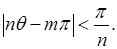
Таким образом, для бесконечного множества значений 
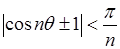 , так что , так что 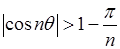 . .
Это также свидетельствует о нарушении необходимого условия сходимости. Если образовать степенной ряд:
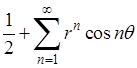 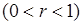
(здесь буква  заменяет прежнюю букву заменяет прежнюю букву 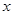 ), то его сумма при значении ), то его сумма при значении 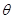 , отличном от 0, будет , отличном от 0, будет
 (3) (3)
и при 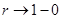 стремится к 0. Таким образом, для стремится к 0. Таким образом, для 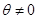 “обобщенной суммой” ряда будет 0. если “обобщенной суммой” ряда будет 0. если 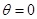 , то ряд (2), очевидно имеет сумму, равную , то ряд (2), очевидно имеет сумму, равную  ; впрочем, выражение (3), которое в этом случае сводится к ; впрочем, выражение (3), которое в этом случае сводится к  , также имеет пределом , также имеет пределом  . .
3) Аналогично ряд
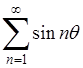  , ,
который сходится лишь при 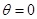 или или  , приводит к степенному ряду , приводит к степенному ряду
 . .
Так что “обобщенная сумма" на этот раз оказывается равной  при при 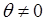 и равной нулю при и равной нулю при 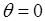 . .
Непосредственно ясно, что рассматриваемый метод “обобщенного суммирования” является линейным. Что же касается регулярности этого метода, то она устанавливается следующей теоремой принадлежащей Абелю.
Теорема. Если ряд (А) сходится и имеет сумму А (в обычном смысле), то для  сходится степенной ряд (1), и его сумма стремится к пределу А, когда сходится степенной ряд (1), и его сумма стремится к пределу А, когда 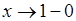 . .
Доказательство. Начнем с того, что радиус сходимости ряда (1) не меньше 1, так что для  ряд (1), действительно, сходится. Мы имели уже тождество
ряд (1), действительно, сходится. Мы имели уже тождество

(
где  ); вычтем его почленно из тождества ); вычтем его почленно из тождества
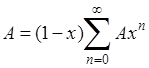 . .
Полагая 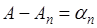 , Придем к тождеству , Придем к тождеству
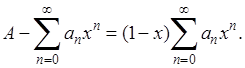 (4) (4)
Так как 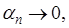 то по произвольно заданному то по произвольно заданному  найдется такой номер найдется такой номер  , что , что  , лишь только , лишь только  . .
Разобьем сумму ряда в правой части (4) на две суммы
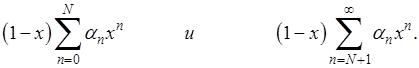
Вторая оценивается сразу и независимо от 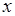 : :
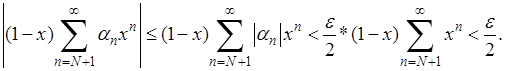
Что же касается первой, то она стремится к 0 при 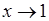 и при достаточной близости и при достаточной близости 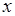 к 1 будет к 1 будет

так что окончательно 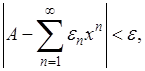 что и доказывает утверждение. что и доказывает утверждение.
Если ряд (А) суммируем по Пуассону-Абелю к сумме А, то в обычном смысле, как мы видели, он может и не иметь суммы. Иными словами из существования предела
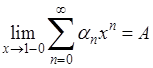 , (5) , (5)
вообще говоря, не вытекает сходимость ряда (А
). Естественно возникает вопрос, какие дополнительные условия надлежит наложить на поведение членов этого ряда, чтобы из (5) можно было заключить о сходимости ряда ( ), т.е. о существовании для него суммы ), т.е. о существовании для него суммы 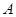 в обычном смысле. Первая теорема в этом направлении была доказана Таубером. в обычном смысле. Первая теорема в этом направлении была доказана Таубером.
Теорема. Пусть ряд (1) сходится при 0<
x<1, и имеет место предельное равенство (5). Если члены ряда (А) таковы, что
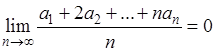 (
6) (
6)
то и 
Доказательство. Разобьем доказательство на две части. Сначала
предположим, что 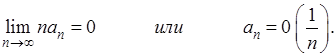 Если положить Если положить 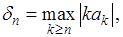 то при то при 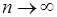 величина величина  , монотонно убывая, стремится к нулю. , монотонно убывая, стремится к нулю.
Имеем при любом натуральном N

так что:

Взяв произвольно малое число 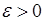 , положим , положим
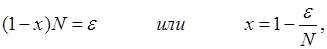
Так что 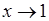 при при  . Пусть теперь . Пусть теперь 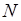 выбрано достаточно большим чтобы: выполнялось неравенство выбрано достаточно большим чтобы: выполнялось неравенство 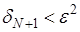 ; соответствующее x
было настолько близко к 1, что ; соответствующее x
было настолько близко к 1, что
 . Тогда . Тогда 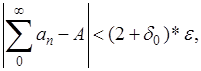
Что и доказывает утверждение теоремы.
К рассмотренному частному случаю теоремы приводится и общий. Положим
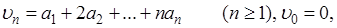 так что так что
 и затем и затем
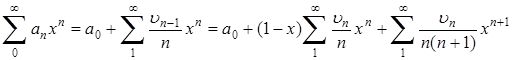 (7) (7)
Но из предположения теоремы, т.е. из того, что  при при 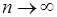 , легко получить, что , легко получить, что
 . (8) . (8)
Для доказательства этого достаточно разбить здесь сумму на две:
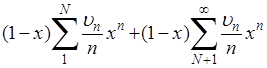
и выбрать N
таким, чтобы во второй сумме все множители  были по абсолютной величине меньшими наперед заданного числа были по абсолютной величине меньшими наперед заданного числа 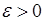 , тогда и вторая сумма по абсолютной величине будет меньше , тогда и вторая сумма по абсолютной величине будет меньше 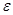 , каково бы ни было х
; относительно первой суммы, состоящей из определенного конечного числа слагаемых, того же можно достигнуть за счет приближения х
к 1. , каково бы ни было х
; относительно первой суммы, состоящей из определенного конечного числа слагаемых, того же можно достигнуть за счет приближения х
к 1.

Но здесь уже можно применить доказанный частный случай теоремы, так что и
 С другой стороны, С другой стороны,

Отсюда, так как первое слагаемое справа стремится к нулю
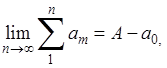
Что и завершает доказательство теоремы.
Идея метода в простейшем его осуществлении принадлежит Фробениусу, но связывают его обычно с именем Чезаро, который дал методу дальнейшее развитие.
По частичным суммам 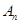 данного числового ряда (А) строятся их последовательные средние арифметические данного числового ряда (А) строятся их последовательные средние арифметические
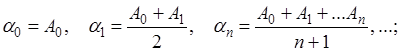
Если варианта  при при 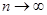 имеет предел А, то это число и называют “обобщенной (в смысле Чезаро) суммой” данного ряда. имеет предел А, то это число и называют “обобщенной (в смысле Чезаро) суммой” данного ряда.
Примеры.1) Возвращаясь к ряду
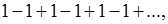 Имеем здесь Имеем здесь
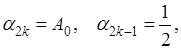
так что 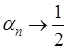 . Мы пришли к той же сумме, что и по методу Пуассона-Абеля. . Мы пришли к той же сумме, что и по методу Пуассона-Абеля.
2) Для ряда 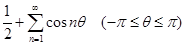 . Частичные суммы будут (если только . Частичные суммы будут (если только 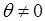 ) )
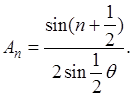
Теперь нетрудно подсчитать средние арифметические:

Итак, окончательно
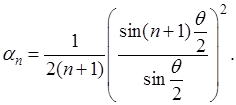
Очевидно, 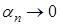 : для значений : для значений 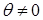 “обобщенной суммой” и здесь служит 0. “обобщенной суммой” и здесь служит 0.
3) Наконец, пусть снова предложен ряд 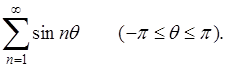
Имеем при 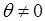 , ,

и затем
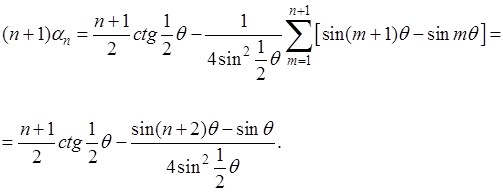
Отсюда ясно, что 
Во всех случаях по методу Чезаро получилась та же “обобщенная сумма", что и выше, по методу Пуассона-Абеля. Оказывается это не случайность.
Начнем с простого замечания: если ряд (А) суммируем по методу средних арифметических к конечной “сумме” А, то необходимо 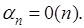
Действительно, из  и и 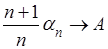 следует, что следует, что
 а тогда и а тогда и
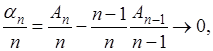
что и требовалось доказать.
Теорема (Фробениуса). Если ряд (А) суммируем по методу средних арифметических к конечной “сумме” А, то одновременно он суммируем также по методу Пуассона-Абеля и притом к той же сумме.
Доказательство. Итак, пусть 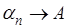 . Ввиду сделанного вначале замечания очевидна сходимость степенного ряда . Ввиду сделанного вначале замечания очевидна сходимость степенного ряда
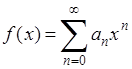
для 0<
x<1.
Выполнив дважды преобразование Абеля, последовательно получим

[при этом следует помнить, что 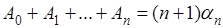 ]. ].
Известно, что (для 0<
x<1
)  или или

Умножим обе части тождества на А
и вычтем из него почленно предыдущее тождество:
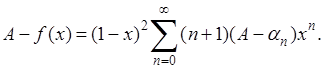
Сумму справа разобьем на две:

Причем число N
выберем так, чтобы при 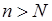 было было
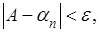
где 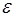 - произвольное наперед заданное положительное число. Тогда вторая сумма по абсолютной величине и сама будет меньше - произвольное наперед заданное положительное число. Тогда вторая сумма по абсолютной величине и сама будет меньше 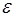 (независимо от (независимо от  ), а для первой суммы того же можно добиться за счет приближения x
к 1. Этим и завершается доказательство. ), а для первой суммы того же можно добиться за счет приближения x
к 1. Этим и завершается доказательство.
Итак, мы установили, что во всех случаях, где приложим метод Чезаро, приложим и метод Пуассона-Абеля с тем же результатом.
Обратное же неверно: существуют ряды суммируемые методом Пуассона-Абеля, но не имеющие “обобщенной суммы" в смысле Чезаро. Рассмотрим, например, ряд

Так здесь явно не соблюдено необходимое условие суммируемости по методу средних арифметических, то этот метод не приложим. В то же время ряд
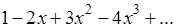
Имеет (при 0<
x<1
) сумму  , которая при , которая при 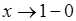 стремится к пределу стремится к пределу 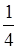 . Это и есть “обобщенная сумма" нашего ряда по Пуассону-Абелю. . Это и есть “обобщенная сумма" нашего ряда по Пуассону-Абелю.
Таким образом, метод Пуассона-Абеля является более мощным, то есть приложим в более широком классе случаев, чем метод Чезаро, но не противоречит ему в тех случаях, когда они оказываются приложимыми оба.
Как и в случае Пуассона-Абеля, для метода Чезаро также могут быть доказаны теоремы “тауберовского” типа, устанавливающие те дополнительные условия относительно членов ряда, при наличии которых из суммируемости ряда по методу средних арифметических вытекает его сходимость в обычном смысле слова. Ввиду теоремы Фробениуса ясно, что каждая тауберовская теорема для метода Пуассона-Абеля приводит, в частности, к такой же теореме для метода Чезаро. Например, сама теорема Таубера перефразируется теперь так: если и выполняется условие и выполняется условие
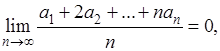 (
9) (
9)
то одновременно и  .
Впрочем, здесь она непосредственно вытекает из легко проверяемого тождества .
Впрочем, здесь она непосредственно вытекает из легко проверяемого тождества
 , ,
которое для данного случая указывает даже на необходимость условия (9).
Харди установил, что заключение от  к к  можно сделать не только, если можно сделать не только, если 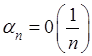 , но и при более широком предположении, что , но и при более широком предположении, что
 ( (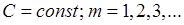 ). ).
Ландау показал, что можно удовольствоваться даже “односторонним” выполнением этого соотношения;
Теорема. Если ряд (А) суммируем к “сумме” А по методу средних арифметических и при этом выполняется условие
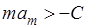 ( (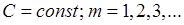 ),то одновременно и ),то одновременно и
 . .
[Изменяя знаки всех членов ряда, видим, что достаточно также предположить неравенство другого смысла:
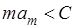 . .
В частности, теорема, очевидно приложима к рядам с членами постоянного знака.
Доказательство. Для доказательства рассмотрим сначала сумму
 , ,
где n
и k
- произвольные натуральные числа; путем тождественного преобразования она легко приводится к виду
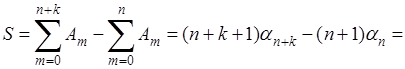
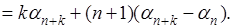 (10) (10)
Если взять любое 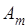 (при (при 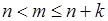 ), то используя предположенное неравенство ), то используя предположенное неравенство  , можно получить такую оценку снизу: , можно получить такую оценку снизу:
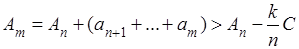 , ,
откуда, суммируя по m
, найдем
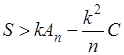 . .
Отсюда, сопоставляя с (10), приходим к такому неравенству:
 . (11) . (11)
Станем теперь произвольно увеличивать п
до бесконечности, а изменение k
подчиним требованию, чтобы отношение  стремилось к наперед заданному числу стремилось к наперед заданному числу 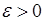 . Тогда правая часть неравенства (11) будет стремиться к пределу . Тогда правая часть неравенства (11) будет стремиться к пределу  , так что для достаточно больших значений п
будет , так что для достаточно больших значений п
будет
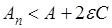 . (12) . (12)
Совершенно аналогично, рассматривая сумму
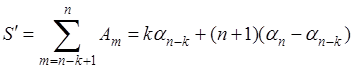
и проведя для 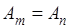 (при (при  ) оценку сверху: ) оценку сверху:
 , ,
придем к неравенству
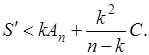
Отсюда

Если 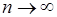 и одновременно и одновременно  , как и прежде (но на этот раз пусть , как и прежде (но на этот раз пусть  ), то правая часть этого неравенства стремится к пределу ), то правая часть этого неравенства стремится к пределу
 . .
Следовательно, для достаточно больших n
окажется
 . (13) . (13)
Сопоставляя (12) и (13), видим, что, действительно,
 . .
Теорема доказана.
Остановимся на применении обобщенных методов суммирования в вопросе об умножении рядов по правилу Коши. Пусть, кроме ряда (А
), дан ещё ряд
 (В
) (В
)
тогда ряд
 (С
) (С
)
и называется произведением рядов (А
) и (В
) в форме Коши. Если данные ряды сходятся и имеют обыкновенные суммы А
и В,
то ряд (С
) все же может оказаться расходящимся.
Однако во всех случаях ряд (С) суммируем по методу Пуассона-Абеля и именно к сумме АВ.
Действительно, для 0<
x<1
ряд (1) равно как и ряд
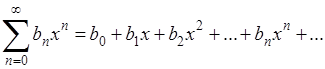
оба абсолютно сходятся; обозначим их суммы, соответственно, через  и и  . Произведение этих рядов, то есть ряд . Произведение этих рядов, то есть ряд
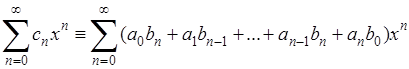 , ,
По классической теореме Коши также сходится и имеет суммой произведение  * * . Эта сумма при . Эта сумма при 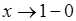 стремится к АВ
, ибо как мы видели, по отдельности стремится к АВ
, ибо как мы видели, по отдельности

Итак, “обобщенной (в смысле Пуассона-Абеля) суммой” ряда (С)
действительно будет АВ,
что и требовалось доказать.
Отсюда как следствие получается теорема Абеля об умножении рядов. Равным образом из самого доказательства ясно, что то же заключение остается в силе, если ряды (А) и (В) -
вместо того, чтобы сходиться в собственном смысле - лишь суммируемы по методу Пуассона-Абеля к суммам А и В.
В таком случае, учитывая теорему Фробениуса, можно сделать и следующее утверждение: если (А), (В) и (С) суммируемы в смысле Чезаро и имеют, соответственно, “обобщенные суммы" А, В и С, то необходимо С=АВ.
В качестве примера рассмотрим возведение в квадрат ряда
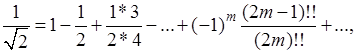
который получается из биномиального разложения
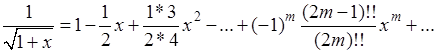
при х=1
. умножая указанный числовой ряд на самого себя, придем к хорошо знакомому нам ряду

“обобщенная сумма" которого есть 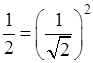 . .
Далее, “возведем в квадрат" и этот расходящийся ряд. Мы получим ряд
 “обобщенная сумма" которого в смысле Пуассона-Абеля есть “обобщенная сумма" которого в смысле Пуассона-Абеля есть  . .
Пусть мы имеем положительную числовую последовательность  и и
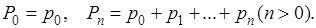
Из частичных сумм  ряда (А
) составим выражения ряда (А
) составим выражения

Если  при при  то А
называется “обобщенной суммой” ряда (А)
в смысле Вороного - при заданном выборе последовательности то А
называется “обобщенной суммой” ряда (А)
в смысле Вороного - при заданном выборе последовательности  . .
Теорема.
Для регулярности метода Вороного необходимо и достаточно условие.

Доказательство. Необходимость.
Допустим сначала регулярность рассматриваемого метода: пусть из  всегда следует и всегда следует и  . Если, в частности, взять ряд . Если, в частности, взять ряд  для которого для которого 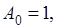 а прочие а прочие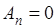 (так что и (так что и 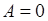 ), то необходимо ), то необходимо

Достаточность. Предположим теперь условие теоремы выполненным и докажем, что из  вытекает и вытекает и  . .
Обратимся к теореме Теплица и заменим там 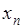 на на  и и 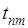 на на 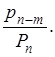 Условие (а) этой теоремы удовлетворено, ибо Условие (а) этой теоремы удовлетворено, ибо

Выполнение условий (б) и (в) очевидно, так как

Следовательно, как и требовалось доказать,  . .
Мы уже знакомы с методом средних арифметических; он является простейшим из бесконечной последовательности методов суммирования, предложенных Чезаро.
Фиксируя натуральное число к
, Чезаро вводит варианту
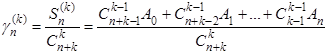
и ее предел при 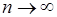 рассматривает как “обобщенную сумму" (к
-го порядка) ряда (А
). При к
=1 мы возвращаемся к методу средних арифметических. рассматривает как “обобщенную сумму" (к
-го порядка) ряда (А
). При к
=1 мы возвращаемся к методу средних арифметических.
В дальнейшем нам не раз понадобится следующее соотношение между коэффициентами:
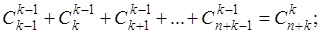
Он легко доказывается по методу математической индукции относительно n,
B и если исходить из известного соотношения
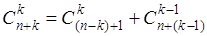 . (14) . (14)
Прежде всего, покажем, что методы Чезаро всех порядков являются частными случаями регулярных методов Вороного.
Для этого достаточно положить 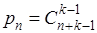 , ибо из (14) тогда следует, что , ибо из (14) тогда следует, что 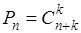 и к тому же, очевидно, и к тому же, очевидно,
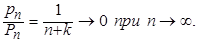
С помощью того же равенства (14), пользуясь самим определением величин  , устанавливается, что , устанавливается, что
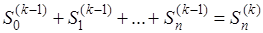 . (15) . (15)
Это дает возможность выяснить взаимоотношение между суммированием по Чезаро к
-го и (к-1
) - го порядка. Пусть ряд (А
) допускает суммирование (к-1
) - го порядка, так что  . В силу (14) и (15) имеем . В силу (14) и (15) имеем

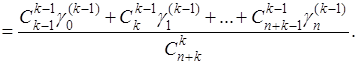
Применяя сюда теорему Теплица, причем полагаем
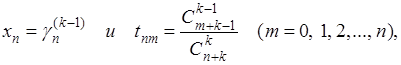
придем к заключению, что и 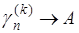 . Таким образом, если ряд (А) допускает суммирование по методу Чезаро какого-нибудь порядка, то он допускает и суммирование любого высшего порядка, и притом к той же сумме. . Таким образом, если ряд (А) допускает суммирование по методу Чезаро какого-нибудь порядка, то он допускает и суммирование любого высшего порядка, и притом к той же сумме.
Приведем теперь обобщение уже известной нам теоремы Фробениуса: если ряд (А) суммируем по какому-либо из методов Чезаро
(скажем к
-го порядка), то он суммируем к той же сумме и по методу Пуссона-Абеля.
Доказательство. Пусть дано, что
 (16) (16)
Легко заключить отсюда, что ряд
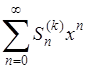 (17) (17)
для - 1<
x<1
сходится. Действительно, так как  то из (16) имеем: то из (16) имеем:
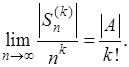
Если 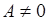 , то , то
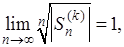
так что по теореме Коши-Адамара, радиус сходимости ряда (17) равен 1. Он во всяком случае не меньше 1, если А
=0.
Рассмотрим теперь ряд тождеств
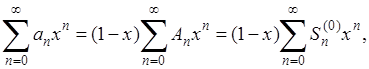
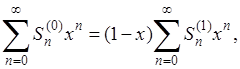 [2] [2]
 
Выше мы установили сходимость последнего ряда в промежутке (-1,1); отсюда вытекает сходимость и всех предшествующих рядов. Кроме того,
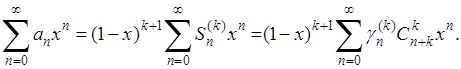 (18) (18)
Сопоставим с этим тождеством другое:
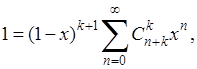 (19) (19)
которое имеет место в том же промежутке (-1;
1);
оно получается к
-кратным дифференцированием прогрессии

Умножив обе части тождества (19) на А
и вычитая из него почленно равенство (18), получим наконец,
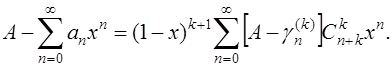
Дальнейшие рассуждения [с учетом (16)] вполне аналогичны тем, с помощью которых была доказана теорема Абеля и теорема Фробениуса. В результате мы и получим:

что и требовалось доказать.
Отметим, что существуют расходящиеся ряды, суммируемые по методу Пуассона-Абеля, но не суммируемые ни одним из обобщенных методов Чезаро. Таким образом, первый из названных методов оказывается сильнее всех последних, даже вместе взятых.
Он состоит в следующем: по ряду (А
) и его частичным суммам 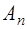 строится выражение: строится выражение:

Если последний ряд сходится, хотя бы для достаточно больших значений х, и его сумма при 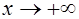 имеет предел А, то это число и является “обобщенной суммой” в смысле Борелядля данного ряда (А). имеет предел А, то это число и является “обобщенной суммой” в смысле Борелядля данного ряда (А).
Докажем регулярность метода Бореля. Допустим сходимость ряда (А
) и обозначим его сумму через А
, а остатки  через через  . Имеем (для достаточно больших х
) . Имеем (для достаточно больших х
)
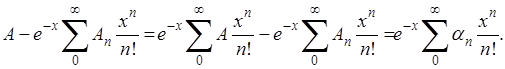
Зададимся произвольно малым числом 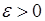 ; найдется такой номер N,
что для ; найдется такой номер N,
что для 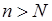 будет: будет:
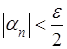 . .
Представим последнее выражение в виде суммы,
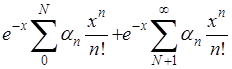 . .
Второе слагаемое по абсолютной величине 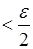 , каково бы ни было х
, а первое представляющее собой произведение , каково бы ни было х
, а первое представляющее собой произведение 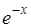 на многочлен, целый относительно х
, становится абсолютно на многочлен, целый относительно х
, становится абсолютно 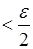 при достаточно больших х
. Этим все доказано. при достаточно больших х
. Этим все доказано.
Пусть дан ряд 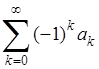 . Формула, выражающая “преобразование Эйлера” выглядит следующим образом . Формула, выражающая “преобразование Эйлера” выглядит следующим образом
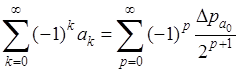 . (20) . (20)
При этом
, как было доказано, из сходимости ряда в левой части вытекает сходимость ряда в правой части и равенство между их суммами
.
Однако и при расходимости первого ряда второй ряд может оказаться сходящимся; в подомном случае его сумму Эйлер приписывал в качестве “обобщенной суммы" первому ряду. В этом собственно и состоит метод Эйлера суммирования рядов; сделанное только что замечание гарантирует регулярность метода.
Если писать рассматриваемый ряд в обычном виде (А
), не выделяя знаков 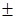 , и иметь в виду вырыжение , и иметь в виду вырыжение
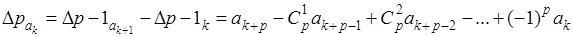
для р-
ой разности, то можно сказать, что методу суммирования Эйлера в качестве “обобщенной суммы" ряда (А
) берется обычная сумма ряда
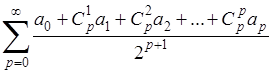
(в предположении, что последний сходится)
Методы Гельдера представляют собой ещё один класс методов обобщенного суммирования. Но они состоят в простом повторении метода средних арифметических. Поэтому рассматривать их не стоит.
В своей дипломной работе я рассмотрел методы суммирования расходящихся рядов, теоремы, вытекающие из этих методов, а также взаимосвязь этих методов между собой. Мы увидели многообразие подходов к вопросу суммирования расходящихся рядов. Регулярность каждого метода мы устанавливали во всех случаях. К сожалению, я не всегда имел возможность достаточно углубиться в вопрос о взаимоотношении этих методов между собой. А между тем может случиться, что два метода имеют пересекающиеся области приложимости, или, наоборот, может оказаться и что два метода приписывают одному и тому же расходящемуся ряду различные “обобщенные суммы”.
Теория рядов является важным и широко используемым разделом математического анализа, или другими словами бесконечные ряды являются важнейшим орудием исследования в математическом анализе и его приложениях.
1. Выгодский М.Я. Справочник по высшей математике. М., 1982.
2. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах, часть 1, М., 1974.
3. Зельдович Я.Б. Высшая математика для начинающих. М., 1970.
4. Леонтьев А.Ф. Целые функции. Ряды экспонент. М., 1983.
5. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления, I, II т., М., 1966.
[1]
Хотя формулировка метода “обобщенного суммирования ” принадлежит Пуассону, этот метод называют всё же методом Абеля, так как Пуассон применил этот метод лишь в частном случае. Поэтому в дальнейшем мы будем называть этот метод – методом Пассона-Абеля.
[2]
Здесь и дальше учитываются соотношения типа (15)
|