Содержание
1. Анализ рядов распределения
2. Анализ рядов динамики
3. Индексы
4. Выборочное наблюдение
Список литературы
1. Анализ рядов распределения
По данным ряда распределения своего вариант (табл. I) выполнить следующие расчеты. 1.1. Построить ряд распределения. Изобразить ряд графически в виде гистограммы (полигона) и кумуляты распределения. Сделать вывод о характере распределения. 1.2. Рассчитать моду, медиану, первый и третий квартиль. 1.3. Рассчитать средний уровень признака в совокупности; сравнить значение моды, медианы, средней и сделать вывод об асимметрии распределения. 1.4. Рассчитать показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации. 1.5. Указать другие методы расчета среднего уровня и дисперсии. 1.6. Показать методику расчет дисперсии альтернативного признака. 1.7. Назвать виды дисперсии в совокупности, разбитой на группы, сформулировать правило их сложения и методику расчета показателя тесноты связи между изучаемыми признаками.
Решение
1.1. Построим ряд распределения.
Таблица А
Распределение покупателей по стоимости покупок канцелярских товаров
| Группы по стоимости покупок |
Частота |
| 18 – 24 |
18 |
| 24 – 28 |
27 |
| 28 – 32 |
35 |
| 32 – 36 |
41 |
| 36 – 40 |
30 |
| 40 – 44 |
21 |
| 44 и выше |
15 |
| Итого (объем ряда) |
159 |
Гистограмма (полигон)
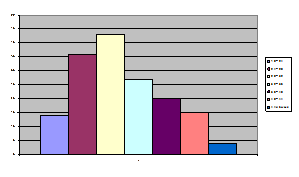
Кумулята распределения.

По виду графиков делаем вывод о нормальном распределении признака.
1.2. Рассчитаем моду, медиану, первый и третий квартиль.
Модальным является интервал (28, 32), содержащий наибольшее число покупателей. Модальный размер стоимости покупок:
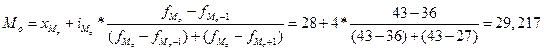
Медиана определяется по формуле:
 . .
Медианным интервалом является интервал [28 - 32], содержащий 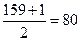 -го покупателя. Медианный размер стоимости покупок: -го покупателя. Медианный размер стоимости покупок:
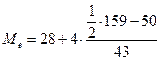 =30,774. =30,774.
Первый квартиль определяется по формуле:
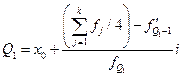
Он задается интервалом [24 - 28], содержащим  -го покупателя. -го покупателя.

Третий квартиль определяется по формуле
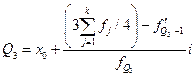
Он задается интервалом [32 - 36], содержащим 3* -го покупателя. -го покупателя.

1.3. Переходим от интервального ряда к моментному, приняв за стоимость покупок середину соответствующего интервала.
| №интервала |
СерединаИнтервала( ) ) |
ЧислоПокупателей(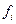 ) ) |
 |
| 1 |
21 |
14 |
294 |
| 2 |
26 |
36 |
936 |
| 3 |
30 |
43 |
1290 |
| 4 |
34 |
27 |
918 |
| 5 |
38 |
20 |
760 |
| 6 |
42 |
15 |
630 |
| 7 |
46 |
4 |
184 |
| Всего |
159 |
5012 |
Находим средний уровень признака в совокупности по формуле средней арифметической взвешенной:
 . .
Получаем:  5012/159=31,522. 5012/159=31,522.
Так как мода и медиана меньше среднего уровня признака, то коэффициент асимметрии положителен.
1.4. Для расчетов показателей вариации составляем вспомогательную таблицу.
| №интервала |
Середина
интервала
( ) )
|
Число
покупателей
(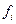 ) )
|
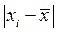 |
 |
 |
 |
| 1 |
21 |
14 |
10,522 |
147,308 |
110,713 |
1549,978 |
| 2 |
26 |
36 |
5,522 |
198,792 |
30,493 |
1097,734 |
| 3 |
30 |
43 |
1,522 |
65,447 |
2,317 |
99,610 |
| 4 |
34 |
27 |
2,478 |
66,906 |
6,140 |
165,791 |
| 5 |
38 |
20 |
6,478 |
129,560 |
41,964 |
839,286 |
| 6 |
42 |
15 |
10,478 |
157,170 |
109,788 |
1646,823 |
| 7 |
46 |
4 |
14,478 |
57,912 |
209,612 |
838,448 |
| Всего |
159 |
823,094 |
6237,673 |
Размах вариации:
 = 46 – 21=25. = 46 – 21=25.
Среднее линейное отклонение:
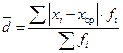 = 823,094/ 159 = 5,177, = 823,094/ 159 = 5,177,
Дисперсия:
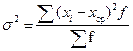 = 6237,673/ 159 = 39,231, = 6237,673/ 159 = 39,231,
Среднее квадратическое отклонение
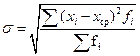 = 6,263, = 6,263,
Коэффициент вариации
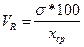 = 6,263*100/ 31,522 = 19,87%. = 6,263*100/ 31,522 = 19,87%.
1.5. Методы расчета среднего уровня:
средний уровень ряда по формуле средней простой
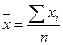 , ,
по формуле средней хронологической

для моментных рядов; по формуле средней гармонической взвешенной
 . .
Дисперсию можно вычислить по формуле:
 . .
1.6. Рассчитать дисперсию альтернативного признака можно следующим образом: вычислить значения  и и  Тогда Тогда  . .
1.7. В совокупности, разбитой на группы можно вычислить:
межгрупповую дисперсия по формуле:

среднюю из групповых дисперсий по формуле:
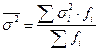
Правило сложения дисперсий
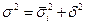 . .
2. Анализ рядов динамики
2.1. Построить ряд динамики. Изобразить ряд в виде линейного графика. Сделать вывод о наличии тенденции изменения уровня и ее характере (увеличение уровня, снижение уровня, переломы тенденции, периоды одинакового типа тенденции).
2.2. Рассчитать среднюю хронологическую (ряд динамики интервальный). При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные хронологические средние.
2.3. Рассчитать систему производных показателей ряда динамики (абсолютные приросты, темпы роста и прироста, абсолютные значения одного процента прироста).
2.4. Показать взаимосвязь цепных и базисных темпов роста и прироста.
2.5. Рассчитать средний абсолютный прирост. При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные абсолютные приросты.
2.6. Рассчитать средний темп роста (три методики расчета). При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные средние темпы роста.
2.7. Проанализировать тенденцию изменения уровня, самостоятельно избрав метод (скользящий средний уровень, аналитическое выравнивание по соответствующей модели). Выровненные значения показать на графике.
2.8. Проанализировать сезонные колебания объема выпуска продукции за три года. Рассчитать индексы сезонности. На графике изобразить сезонную волну.
Решение
2.1. Построим ряд динамики:
| Годы |
Выпуск продукции, тыс.усл.ед. |
| 1 |
1476 |
| 2 |
1529 |
| 3 |
1607 |
| 4 |
1598 |
| 5 |
1673 |
| 6 |
1702 |
| 7 |
1680 |
| 8 |
1658 |
| 9 |
1612 |
| 10 |
1639 |
Изобразим ряд в виде линейного графика.
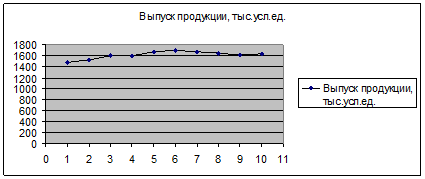
По графику делаем следующие выводы: Первые 6 лет наблюдалось небольшое увеличение выпуска, затем – снижение и в последний год - рост уровня выпуска.
2.2. Так как ряд динамики интервальный среднюю хронологическую вычисляем по формуле:
 = 16174/10= 1617,4. = 16174/10= 1617,4.
Среднее первых 4 лет: (1476+1529+1607+1598)/4= 1552,5
Среднее последних 4 лет: (1680+1658+1612+1639)/4=1647,25
2.3. Рассчитаем систему производных показателей ряда динамики (абсолютные приросты, темпы роста и прироста, абсолютные значения одного процента прироста) по формулам:
Абсолютные приросты:
цепные:  уц
= уi
- yi
-1
базисные: уц
= уi
- yi
-1
базисные:  уб
= уi
- y0 уб
= уi
- y0
Темпы роста:
цепные: Трц
= (уi
/ yi
-1
) базисные: Трб
= (уi
/ y0
)
Темпы прироста:
цепные: Тпр
= Dуц
/ уi-1
, базисные: Тпр
= Dуб
/ y0
Абсолютное значение 1% прироста Аi
= yi
-1
/ 100
Составляем расчетную таблицу:
| Годы |
Выпуск продукции,
тыс.усл.ед.
|
Абсолютные
приросты
|
Темпыроста |
Темпыприроста |
Абсолют. значение
1%приростаед. прод.
|
| Цеп. |
Баз. |
Цеп. |
Баз. |
Цеп. |
Баз. |
| 1 |
1476 |
| 2 |
1529 |
53 |
53 |
1,036 |
1,036 |
0,036 |
0,036 |
14,76 |
| 3 |
1607 |
78 |
131 |
1,051 |
1,089 |
0,051 |
0,089 |
15,29 |
| 4 |
1598 |
-9 |
122 |
0,994 |
1,083 |
-0,006 |
0,083 |
16,07 |
| 5 |
1673 |
75 |
197 |
1,047 |
1,133 |
0,047 |
0,133 |
15,98 |
| 6 |
1702 |
29 |
226 |
1,017 |
1,153 |
0,017 |
0,153 |
16,73 |
| 7 |
1680 |
-22 |
204 |
0,987 |
1,138 |
-0,013 |
0,138 |
17,02 |
| 8 |
1658 |
-22 |
182 |
0,987 |
1,123 |
-0,013 |
0,123 |
16,8 |
| 9 |
1612 |
-46 |
136 |
0,972 |
1,092 |
-0,028 |
0,092 |
16,58 |
| 10 |
1639 |
27 |
163 |
1,017 |
1,110 |
0,017 |
0,110 |
16,12 |
| сумма |
16174 |
163 |
2.4. Взаимосвязь цепных и базисных темпов роста и прироста:
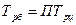
2.5. Средний абсолютный прирост
исходя из цепных абсолютных приростов:
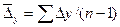 =163/9= 18,111 =163/9= 18,111
исходя из базисного абсолютного прироста:
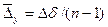 =18,111. =18,111.
Средний абсолютный прирост первых 6 лет: 226/5= 45,2
Средний абсолютный прирост последних 5 лет: (163-226)/4= -15,75
2.6. Средний темп роста:
 (101,2%). (101,2%).
Средний темп прироста:
 .
.
Средний темп роста первых 6 лет:  . .
Средний темп роста последних 5 лет: 
2.6. Аналитическое выравнивание проведем по методу скользящей средней. Находим средние значения признака для каждой тройки соседних лет.
| Годы |
Выпуск продукции,
тыс.усл.ед.
|
Средние значения для
тройки соседних лет
|
| 1 |
1476 |
| 2 |
1529 |
| 3 |
1607 |
1537,3 |
| 4 |
1598 |
1578 |
| 5 |
1673 |
1626 |
| 6 |
1702 |
1657,7 |
| 7 |
1680 |
1685 |
| 8 |
1658 |
1680 |
| 9 |
1612 |
1650 |
| 10 |
1639 |
1636,3 |
Выровненные значения показываем на графике.
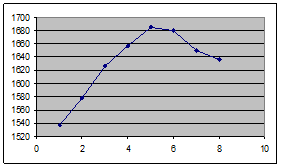
Вывод.
При использовании метода аналитического выравнивания динамического ряда и отображения результатов графически прослеживается тенденция увеличения выпуска продукции первые 5 лет и дальнейшее снижение выпуска продукции. Эти результаты подтверждаются расчетом частных средних абсолютных приростов и темпов роста.
2.8. Проанализируем сезонные колебания объема выпуска продукции за три года. Построим динамическую таблицу, содержащую объем выпуска продукции за три года.
Таблица В Динамика помесячного выпуска продукции
| Месяц |
Год |
| первый |
второй |
третий |
| 1 |
287 |
295 |
302 |
| 2 |
262 |
280 |
292 |
| 3 |
284 |
298 |
314 |
| 4 |
335 |
350 |
327 |
| 5 |
354 |
363 |
329 |
| 6 |
362 |
384 |
392 |
| 7 |
380 |
392 |
397 |
| 8 |
387 |
398 |
403 |
| 9 |
330 |
358 |
411 |
| 10 |
321 |
319 |
403 |
| 11 |
301 |
307 |
364 |
| 12 |
274 |
265 |
315 |
Рассчитаем индексы сезонности по формуле:
 , ,
где,  - средняя за месяц, - средняя за месяц, 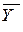 - средняя за год. - средняя за год.
Определим осредненные значения уровней для каждого месяца годового цикла, среднюю за год, индексы сезонности.
| Месяц |
Осредненное значение уровня |
Индексы сезонности |
| расчет |
итого |
0,860116 |
| 1 |
(287+295+302)/(31+31+31) |
9,505 |
0,86743 |
| 2 |
(262+280+292)/(29+29+29) |
9,586 |
0,871792 |
| 3 |
(284+298+314 )/(31+31+31) |
9,634 |
1,01748 |
| 4 |
(335+350+327)/(30+30+30) |
11,244 |
1,017739 |
| 5 |
(354+363+329)/(31+31+31) |
11,247 |
1,144162 |
| 6 |
(362+384+392)/(30+30+30) |
12,644 |
1,137416 |
| 7 |
(380+392+397)/(31+31+31) |
12,570 |
1,155903 |
| 8 |
(387+398+403)/(31+31+31) |
12,774 |
1,104951 |
| 9 |
(330+358+411)/(30+30+30) |
12,211 |
1,01482 |
| 10 |
(321+319+403)/(31+31+31) |
11,215 |
0,977263 |
| 11 |
(301+307+364)/(30+30+30) |
10,800 |
0,830927 |
| 12 |
(274+265+315)/(31+31+31) |
9,183 |
0,860116 |
| Сумма |
|
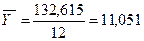
На графике изобразим сезонную волну:

3. Индексы
3.1. Рассчитать индивидуальные индексы цен и физического объема.
3.2. Рассчитать общий индекс цен в агрегатной форме по методикам Пааше, Ласпейреса.
3.3. Рассчитать общий индекс физического объема в агрегатной форме.
3.4. Рассчитать общий индекс стоимости. Показать взаимосвязь индексов цены, физического объема и стоимости.
3.5. Рассчитать влияние факторов на изменение общей стоимости товаров.
3.6. Показать методику преобразования общих индексов цен (Пааше, Ласпейреса) и общего индекса физического объема в средние индексы. Рассчитать общие индексы цен методом среднего индекса.
Решение
Исходные данные:
Цены и физический объем реализованной продукции (цена в рублях, физический объем в тысячах условных единицах)
| Товар-представитель |
| А |
Б |
В |
Г |
| цена |
физ. объем |
цена |
физ. объем |
цена |
физ. объем |
цена |
физ. объем |
| Базовый период |
13,2 |
400 |
3,8 |
2540 |
25,7 |
184 |
83,5 |
156 |
| Текущий период |
11,2 |
403 |
3,1 |
2564 |
29,5 |
194 |
80,9 |
175 |
3.1. Индивидуальные индексы находим по формулам:
 -индивидуальный индекс цен, -индивидуальный индекс цен,
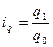 -индивидуальный индекс физического объема продаж. -индивидуальный индекс физического объема продаж.
Результаты вычислений представляем в таблице:
Товар-
представитель
|
Базовый период |
Текущий период |
Индиви-дуальный индекс цен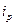 |
Индивидуальный индекс физического объема продаж
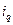
|
цена.

|
объем

|
цена
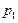
|
объем
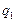
|
| А |
13,2 |
400 |
11,2 |
403 |
0,848 |
1,008 |
| Б |
3,8 |
2540 |
3,1 |
2564 |
0,816 |
1,009 |
| В |
25,7 |
184 |
29,5 |
194 |
1,148 |
1,054 |
| Г |
83,5 |
156 |
80,9 |
175 |
0,969 |
1,122 |
3.2. Рассчитаем общий индекс цен в агрегатной форме по методикам Пааше, Ласпейреса.
Товар-
предс-тавитель
|
Базовый период |
Текущий период |
Стоимость продукции |
| в текущих ценах |
текущего
периода в сопоста-вимых ценах
|
базового
периода в текущих ценах
|
цена,
руб.
|
объем,
тыс. ед.
|
цена,
руб.
|
объем,
тыс. ед.
|
2003 года |
2004 года |
| Символ |
 |
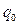 |
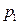 |
 |
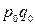 |
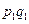 |
 |
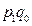 |
| А |
13,2 |
400 |
403 |
11,2 |
5280 |
4513,6 |
5319,6 |
4480 |
| Б |
3,8 |
2540 |
2564 |
3,1 |
9652 |
7948,4 |
9743,2 |
7874 |
| В |
25,7 |
184 |
194 |
29,5 |
4728,8 |
5723 |
4985,8 |
5428 |
| Г |
83,5 |
156 |
175 |
80,9 |
13026 |
14157,5 |
14612,5 |
12620,4 |
| Сумма |
3280 |
3336 |
32686,8 |
32342,5 |
34661,1 |
30402,4 |
Общий индекс цен Пааше:
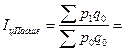 30402,4/ 32686,8=0,93 (93%). 30402,4/ 32686,8=0,93 (93%).
Цены снизились на 7%. Общий индекс цен Ласпейреса:
 32342,5/ 34661,1=0,933 (93,3%). 32342,5/ 34661,1=0,933 (93,3%).
Цены снизились на 6,7%.
3.3. Общий индекс физического объема в агрегатной форме:
 = 34661,1/ 32686,8= 1,06 (106%). = 34661,1/ 32686,8= 1,06 (106%).
Физический объем увеличился на 6%.
3.4. Общий индекс стоимости:
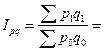 32342,5/ 32686,8 =0,989 (98,9%). 32342,5/ 32686,8 =0,989 (98,9%).
Стоимость уменьшилась на 1,1%. Взаимосвязь индексов:
3.5. Рассчитаем влияние факторов на изменение общей стоимости товаров. Абсолютная сумма изменения общей стоимости товаров:
 32342,5 – 32686,8 = -344,3 32342,5 – 32686,8 = -344,3
- общая стоимость товаров уменьшилась на 344,3 руб.
Абсолютная сумма изменения общей стоимости товаров за счет изменения цен:
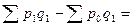 32342,5 - 34661,1 = -2318,6 32342,5 - 34661,1 = -2318,6
- за счет изменения цен общая стоимость товаров уменьшилась на 2318,6 руб.
Абсолютная сумма изменения общей стоимости товаров за счет изменения количества товаров:
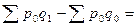 34661,1- 32686,8 = 1974,3 34661,1- 32686,8 = 1974,3
- за счет изменения количества товаров стоимость товаров увеличилась на 1974,3 руб.
3.6. Методик преобразования общих индексов в средние.
Общий индекс цен Пааше:
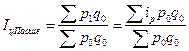 . .
Общий индекс цен Ласпейреса:
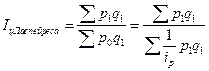 . .
Общий индекс физического объема:
 . .
4. Выборочное
наблюдение
Рассчитать предельную ошибку выборки для средней и для доли с вероятностью, указанной для варианта и границы, в которые попадает генеральная средняя или генеральная доля.
Решение
Исходные данные:
Генеральная численность единиц совокупности N
= 48400.
Выборочная численность единиц совокупности п
= 200.
Средняя  =11,26. =11,26.
Среднее квадратическое отклонение 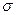 =3,27 =3,27
Выборочная доля W
= 0,042.
Вероятность, с которой гарантируется результат F
(
t
)
= 0,997.
Среднюю ошибку выборки для средней вычисляем по формуле:
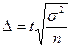 . .
Среднюю ошибку выборки для доли вычисляем по формуле
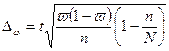 . .
Так как вероятность, с которой гарантируется результат равна 0,997, то уровень коэффициента доверия  . .
Получаем среднюю ошибку выборки для средней: 
Получаем среднюю ошибку выборки для доли:
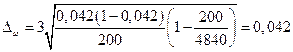
Предельную ошибку выборки вычисляем по формуле:
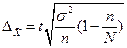 . .
Получаем предельную ошибку выборки для средней:

Границы, в которые попадает генеральная средняя вычисляем по формуле: 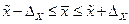 Получаем Получаем 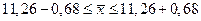 , , 
Генеральная средняя с вероятностью 0,997 находится в интервале от 10,58 до 11,94.
Границы, в которые попадает генеральная генеральная доля вычисляем по формуле:.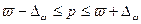 . Получаем: . Получаем: 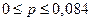 . .
Доля единиц, обладающих определенным свойством с вероятностью 0,997 находится в интервале от 0 до 0,082.
Список литературы
1. Боярский А.Я., Громыко Г.Л. "Общая теория статистики" М.: изд. Московские университеты, 1985 г.
2. Гришин А.Ф. Статистика: Учеб. Пособие. – М.: Финансы и статистика, 2003. – 240с
3. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник.-М.:ИНФРА – М., 1996.- 416 с.
4. Ефремова М.Р. "Общая теория статистики"; М.: "Инфра-М", 1996
5.
Кильдишев и др. "Общая теория статистики" М.: Финансы и Статистика, 1994 г
6.
Переяслова И.Г., Колбачев Е.Б., Переяслова О.Г.
Статистика. Серия "Высшее образование". – Ростов н/Д: "Феникс", 2003.- 288 с.
7. Сборник задач по теории статистики: Учебное пособие/Под ред. проф. В.В.Глинского и к.э.н. Л.К.Серга. – М.: ИНФРА-М; 2002.-257 с.
8. Статистика: Учебное пособие/Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; под ред. В.Г.Ионина. – Изд.2-е, перераб. и доп. – М.: ИНФРА-М, 2001.
9. Статистический словарь (под. ред. Ю.А.Юркова) М.: Финстатинформ, 1996
10. Экономическая статистика (под. ред. Ю.Н. Иванова) М.:ИНФРА-М, 1998 Кильдишев и др. "Общая теория статистики" М.: Финансы и Статистика, 1994 г
|