Содержание:
1. Проектирование усиления пролета неразрезного многопролетного ригеля рамы.
1.1 Исходные данные на проектирование усиления пролета неразрезного многопролетного ригеля рамы
1.2. Расчет несущей способности ригеля в пролете и на опорах.
1.3. Перераспределение моментов
1.4.Расчет арматуры усиления на правой опоре
1.5 Расчет несущей способности ригеля
1.6 Расчет сечения затяжки
1.7 Расчет сближения тяжей затяжки.
1.8 Расчет системы ригель-затяжка
1.9. Построение эпюр изгибающих моментов и перерезывающих сил в ригеле с учетом влияния затяжки
1.10 Проверка прочности ригеля наклонным сечениям
1.11 Проверка прогиба ригеля после усиления
2. Проектирование усиления железобетонной колонны, преднапряженной стальными распорками
2.1. Исходные данные на проектирование усиления железобетонной колонны
2.2 Расчет требуемого сечения уголков распорки
2.3 Расчет соединительных планок
2.4. Расчет ветви распорки на устойчивость при ее предварительном напряжении.
2.5 Расчет бокового смещения “Х” в месте изгиба уголков.
2.6. Расчет сварных швов крепления планок-упоров к уголкам распорок.
Список литературы9
1. Проектирование усиления пролета неразрезного многопролетного ригеля рамы.
1.1. Исходные данные на проектирование усиления пролета неразрезного многопролетного ригеля рамы
Пролет ригеля - 9м.
Размеры сечения ригеля h=75см, b=30см, h0
= h – 5 = 70см.
Кубиковая прочность бетона Rкуб
=37,5МПа
Рабочая арматура класса А-III
В середине пролета 3Ø28
На левой опоре 3Ø28
На правой опоре 3Ø28
Поперечная арматура класса А-III
На приопорном участке 3Ø10, S=2см
В средней части пролета 3Ø10, S=50см
Монтажная арматура класса A-IIØ10.
Полная нагрузка до усиления 80кН/м, после усиления 97,4кН/м
Изгибающие моменты от расчетной нагрузки
после усиления Моп.лев
=594,1кНм, Мпр
=462,7кНм, Моп.пр.
=452,2кНм
Поперечные перерезывающие силы Qлев
=360кН, Qпр
= 360кН.
В результате испытания неразрушающими методами установлено , что бетон имеет кубиковую прочность Rкуб
=37,5МПа, что в соответствии [2, п.6,15] соответствует классу бетона В=0,8·37,5=30 (В30), для которого Rb
=17·γb
2
=17·0.9= =15.3МПа. Расчетное сопротивление арматурной стали в соответсвии с [1, п.6,18] равно  , Rsc
= 339МПа. Расчетное сопротивление арматуры Rsw
= Rs
·0.8·0.9 = 339·0.8·0.9 = 244МПа. , Rsc
= 339МПа. Расчетное сопротивление арматуры Rsw
= Rs
·0.8·0.9 = 339·0.8·0.9 = 244МПа.
Расчетное сопротивление бетона на растяжение:
Rbt
=1.05γb
2
= =1.05·0.9=0.95МПа.

Рис 1 – Ригель.
1.2 Расчет несущей способности ригеля в пролете и на опорах
Высота сжатой зоны 
Относительная высота сжатой зоны 
Mнес
= Rs
As
h0
(1-0.5ξ) = 339·18.47·10-1
·0.7(1-0.5·0.19)= 397кНм.
В результате расчета ригеля в составе рамы (в предположении упругой работы конструкций) на нагрузки, которые увеличатся после усиления получаем:
После усиления:
Постоянная - 29,22кН/м
 Длительная - Длительная -
Временная -
Кратковременная - 34,09кН/м
Σ97,4кН/м
Моп.лев
=594,1кНм, Мпр
=462,7кНм, Моп.пр.
=452,2кНм
Полная нагрузка до усиления 80кН/м.
Балочный момент Мб
= 462,7 + 0,5(594,1 + 452,2) = 986кНм
Проверка  кНм кНм

Рис 2 – Эпюра моментов в ригеле от полной нагрузки.
1.3
Перераспределение моментов
Возможно, уменьшить опорные моменты при увеличении пролетного момента с учетом неупругих деформаций железобетона (в соответствии с руководством по расчету статически неопределимых железобетонных конструкций).
Опорные моменты можно уменьшить на 30%.
Тогда получаем Mлев,
min
= 0,7·594,1 = 416кНм, что больше Мнес
= 397кНм, следовательно здесь требуется усиление.
Mпр,
min
= 0,7·462,7 = 324кНм, что меньше Мнес
= 397кНм, следовательно здесь усиление не требуется.
На левой опоре требуется рассчитать арматуру на величину разности моментов ΔМ = 416 - 397 = 19кНм
Конструкция усиления левой опоры ригеля показана на рисунке 3:

Рис3 – Усиление левой опоры ригеля.
1.4
Расчет арматуры усиления на правой опоре

 0,0074 0,0074
 м2 м2
Принимаем 2Ø10A-IIIAs
=1,57см2
Так как полученное решение приближенно, тк не найден общий центр тяжести арматуры необходимо проверить несущую способность балки на левой опоре – Млев, нес
.
Рассчитываем положение общего центра тяжести сечения арматуры с нахождением h0
.
Статический момент площади всей арматуры относительно оси 0-0:
ΣS0-0
=3AØ28
·70 + 2 AØ10
·75 = 18.47·70 + 1.57·75 = 1410,7см
ΣАS
= 18.47 + 1.57 = 20.04см2
Рабочая высота сечения  см см
Относительная высота сжатой зоны:
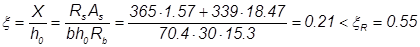
Проверка выполняется
Плечо внутренней пары сил Z = h0
– 0.5·ξh0
= 70.4 – 0.5·0.21·70.4 = 63м.
1.5
Расчет
несущей способности ригеля
Несущая способность ригеля на правой опоре
Млев, нес
= ΣRS
AS
Z = (339·18.47+ 365·1.57)·10-1
·0.63 = 431кНм
Что более Mлев,
min
= 416кНм
В результате перераспределения момент в опоре увеличивается:
Мпр
= Мб
-0,5(Млев,оп
+ Мпр,оп
) = 986 – 0,5(416 + 397) = 580кНм
Эпюра моментов в ригеле после их перераспределения вследствие неупругих деформаций приведена на рисунке
Найдем опорные реакции


В пролете часть момента (Мп
=397кНм) передается на основную арматуру, затяжки.
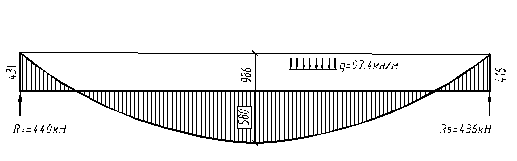
Рис 4 – Эпюра моментов в ригеле после их перераспределения вследствие неупругих деформаций
1.6
Расчет сечения затяжки
Момент передаваемый на затяжку (и соответствующую сжатую зону бетона) равен:
Мз
= Мпр
- Млев
= 580 – 397 = 183кН
Принимаем затяжку из двух стержней Ø25 A-III(Аз
=9,82см2
)
Проверяем прочность ригеля с затяжкой по нормальным сечениям (метод Поповича):
1.  см2 см2
2. 
3, 
4, Mнес
= Rs
·Ared
·hred
(1-0.5ξ) = 339·29·10-1
·0.74(1-0.5 ·0.29) = 622кНм
Так как Mнес
= 622кНм > Mmax
= 580кНм Условие прочности удовлетворяется.

Рис 5 – Усиление ригеля затяжкой.
1.7
Расчет сближения тяжей затяжки
Величина напряжения затяжки назначается в пределах 09Rs
,
ser
≥σр
≥0,3Rs
,
ser
.
Чем больше величина предварительного напряжения , тем больше величина начальной разгрузки балки, но тем меньше затяжка в состоянии воспринимать увеличение напряжений при увеличении нагрузки. Кроме того, увеличение преднапряжений повышает изгибную жесткость балки, что бывает необходимо для обеспечения предельного изгиба.
Принимаем σр
= 0,3Rs
,
ser
= 0,3·390 = 117МПа. Принимаем σр
= 120МПа.
Для обеспечения принятой величины напряжения σр
необходимо определить степень затягивания гайки стяжного болта, что контролируется по зазору между тяжами (сближение тяжей).
Выполняем расчет сближения тяжей (расчетная схема приведена на рис. 6)

Рис 6 – Расчетная схема сближения тяжей.
Удлинение тяжа, при напряжении σр
= 120МПа:

Боковые смещения: 
Величина сближения тяжей δ = B-2a = 300-2·105 = 90мм.
1.8
Расчет системы ригель-затяжка
Исходные данные:
Eb
=32500МПа; ЕS
=200000МПа; AS
=18.47см2
; Ab
=0.3·0.75=0.225м2
hз
= 0,816м; tgα=0.3; cosα=0.958; sinα=0,287.
Момент инерции сечения ригеля:

Параметры:
 0,962 0,962


 0,509 0,509
Усилие в шпренгеле от предварительного напряжения:
D = 0.826P·tgα = 0.826·118·0,3 = 29 кН
где Р = σр
Аз
= 120·9,82·10-1
= 118кН – усилие затяжке от предварительного преднапряжения/
Опорный момент М0
= 0,33Рhз
= 0,33·118·0,816 = 32кНм
После усиления нагрузка на ригель увеличится на 97,4 – 80 = 17,4кН/м
При этом усилие в затяжке повысится на величину:
X = Aql2
ω = 0.509·17.4·92
·0.061 = 44кН
А в шпренгеле: в = 0.826·X·tdα = 0.826·44·0.3 ≈ 11кН.
Опорный момент: М0
= 0,33Xhз
= 0,33·44·0,816 ≈12кНм
Коэффициент ω = 0,061 найден по [2, таб. 6] при полном загружении пролета равномерно распределенной нагрузкой q при x/l = 1.
Суммарные усилия ΣD = 29 + 11 = 40 кН
ΣM0
= 32 + 12 = 44кНм
1.9
Построение эпюр изгибающих моментов и перерезывающих сил в ригеле с учетом влияния затяжки
Определение опорных реакций: RA
= 440 – 40 = 400кН
RВ
= 436 –40 = 396кН
Определение моментов:
Млев,оп
= 431 – 44= 387кН
Мправ,оп
= 397 - 44 = 353кН
Мпр
= - 387 - 97,4·4,52
·0,5 + 40·2 + 400·4,5 = 507 кНм

Рис 7 – а. эпюра изгибающих моментов в ригеле с учетом влияния затяжки; б. Эпюра перерезывающих сил с учетом затяжки.
1.10 Проверка прочности ригеля наклонным сечениям
1. На приопорном участке
 1,396; h0
= 0.7 < C0
≤ 2h0
= 1.4м. 1,396; h0
= 0.7 < C0
≤ 2h0
= 1.4м.
 кН кН
Qsw
= qsw
C = 230·1,396 = 321Кн
где qsw
=  кН/м кН/м
Так как Q = 400кН < Qb
+ Qsw
= 200 + 321 = 521Кн, Условие прочности выполняется.
2. В середине пролета
 1,78; Принимаем 2h0
= 1.4м. 1,78; Принимаем 2h0
= 1.4м.
 кН кН
Qsw
= qsw
C = 115·1,4 = 161Кн
где qsw
=  кН/м кН/м
Так как Q = 156,5 кН < Qb
+ Qsw
= 200 + 161 = 361Кн, Условие прочности выполняется.
1.10 Проверка прогиба ригеля после усиления
Расчет выполняется на действие нормативных нагрузок при среднем коэффициенте надежности по нагрузке γfm
= 1.15
Определение моментов:
Млев,оп
=  кН кН
Мправ,оп
= 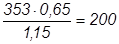 кН кН
Мпр
=  кН кН

Рис 8 - Эпюра изгибающих моментов в ригеле от действия постоянной и длительной накгрузки.
Прогиб определяется от действия постоянной и длительной нагрузки (продолжительное действие нагрузки при коэффициенте  =0,15 [1, таб. 35]. В соответствии с исходными данными составит 65% от полных нагрузок. =0,15 [1, таб. 35]. В соответствии с исходными данными составит 65% от полных нагрузок.
Погиб в середине пролета для ригеля с защемленными опорами определяется по [3, (313)]:


где , , ,  - кривизны в середине пролета, на левой и правой опорах. - кривизны в середине пролета, на левой и правой опорах.
При равномерно распределенной нагрузке к = , тогда прогиб: , тогда прогиб:

1. Вычислим кривизну  в середине пролета ригеля: в середине пролета ригеля:
Определим параметры:
 0,091 0,091
 0,0088; 0,0088;  ; µα = 0,055 ; µα = 0,055
 0,023, где A’s
= 2.36см2
– монтажная арматура Ø10 A-II. 0,023, где A’s
= 2.36см2
– монтажная арматура Ø10 A-II.

Относительная высота сжатой зоны:
 0,216 0,216
Плечо внутренней пары сил при 2a’ =2·3 = 6см
 69,12 69,12
Коэффициент  - - 1.008 1.008
Коэффициент φl
3
= 0.8 (1,табл. 36); Wpl
= γW0
= 1.75
Так как φs
> 1, принимаем φs
= 1.
Кривизна ригеля в пролете:
  = 0,0039 1/м = 0,0039 1/м
2. Вычисляем кривизну  на левой опоре: на левой опоре:
 0,068 0,068
 0,0095; 0,0095;  ; µα = 0,059 ; µα = 0,059
 0,18, 0,18,
 0,17 0,17
Относительная высота сжатой зоны:
 0,181 0,181
Плечо внутренней пары сил при 2a’ =2·5 = 10см
 64,5 64,5
Коэффициент  - - 0,926 0,926
Коэффициент φl
3
= 0.8 (1,табл. 36); Wpl
= γW0
= 1.75
Кривизна ригеля в пролете:
  = 0,00224 1/м = 0,00224 1/м
3. Вычислим кривизну ригеля  на правой опоре: на правой опоре:
 0,062 0,062
 0,0088; 0,0088;  ; µα = 0,055 ; µα = 0,055
 0,182 0,182

Относительная высота сжатой зоны:
 0,174 0,174
Плечо внутренней пары сил при 2a’ =2·5 = 10см
 67 67
Коэффициент  - - 0,896 0,896
Кривизна ригеля в пролете:
  = 0,00221 1/м = 0,00221 1/м
Прогиб, защемленного на опорах ригеля в середине пролета от постоянной и длительной нагрузки:
 =(0,104·0,0039 – 0,0104(0,0024 + 0,0021))92
= 0,029м =(0,104·0,0039 – 0,0104(0,0024 + 0,0021))92
= 0,029м
Предельный прогиб для пролета 9м: [f] =  см см
Так как f = 2,9см < [f] = 4,3см, проверка прогиба проходит.
2. Проектирование усиления железобетонной колонны, преднапряженной стальными распорками
2.1. Исходные данные на проектирование усиления железобетонной колонны
Сечение колонны 40х40см, h0
= 40-5=35мс.
Высота колонны H = Lef
= 4.2м
Кубиковая прочность бетона Rкуб
=18,75МПа; B = 0.8Rкуб
=0.8·18.75=15 (B15)
Rb
= 0.9·8.5 = 7.65МПа
Арматура класса A-II 8Ø36,  ; RSC
=256.5МПа, ; RSC
=256.5МПа,
A’s
= As
= 40,72см2
.
После усиления на колонну будут действовать усилия
От полной нагрузки М=51кНм, N=3527кН.
От постоянной и длительной нагрузки Мдл
=8,3кНм, Nдл
=2410кН.
Стальную распорку выполнить из стали ВСт3кп2-1, Ry
= 220МПа.

Рис 9 – Сечение колонны.
2.2. Расчет несущей способности колонны до усиления
Случайный эксцентриситет
Гибкость:
I = 0.289h = 0.289·0.4 = 0.12м – радиус инерции.

Так как гибкость λ = 35 > 14, то в рачсете учитывается коэффициент продольного изгиба η.
Коэффициент, учитывающий длительность действия нагрузки:  
 -относительный эксцентриситет. -относительный эксцентриситет.
δe
,
min
= 0,5-0,01
 м4
– момент инерции сечения колонны. м4
– момент инерции сечения колонны.
Js
= 2As
0.152
= 2·40.72·0.152
·10-4
= 1.8·10-4
м4
Критическая сила:

 =18510кН =18510кН
Коэффициент продольного изгиба:
 1,23 < 3 1,23 < 3
Определяем случай расчета при симметричной арматуре:
 3.3 > ξR
= 0.55 – случай малых эксцентриситетов. 3.3 > ξR
= 0.55 – случай малых эксцентриситетов.
Несущая способность определяется из уравнения моментов всех сил относительно менее сжатой арматуры:
Ne = αR
Rb
·bh0
2
+ Rsc
A’s
(h0
-a’)= 0.4·7.65·103
·0.4·0.352
+ 265.5·40.72·10-1
(0.35-0.05)=4 74кН
где e = e0
η + 0.5h –a = 0,013·1,23 + 0,5·0,4 – 0,05 = 0,166м
 =2855кН – первое приближение. =2855кН – первое приближение.
Коэффициент продольного изгиба во втором приближении:
 1,18 1,18
 > ξR
= 0.55 > ξR
= 0.55
e = e0
η + 0.5h –a = 0,013·1,18 + 0,5·0,4 – 0,05 = 0,165м
 =2873кН – второе приближение =2873кН – второе приближение
Коэффициент продольного изгиба тетьем приближении:
 1,184 1,184
 > ξR
= 0.55 > ξR
= 0.55
e = e0
η + 0.5h –a = 0,013·1,184 + 0,5·0,4 – 0,05 = 0,165м
 =2873кН – третье приближение. =2873кН – третье приближение.
При Nнес
=2873кН < N = 3527кН – необходимо усиление колонны.
2.3 Расчет требуемого сечения уголков распорки
В случае малых эксцентриситетов определим требуемые сечения уголков по формуле:

= =0,0017м2 =0,0017м2
гдеe = e0
η1
+ 0.5h – a = 0,013·1,23 + 0,2 -0,05 = 0,166
e0
=  м. м.
γ0
= 0.9 – коэффициент условия работы распорки.
αR
=0,4
Формула Атр
р
получена из условий равенства моментов всех сил относительно сечения менее сжатой арматуры колонны – Аs
: ΣM0
=0 (рис ).
Принимаем уголки, которые в паре представляют одну ветвь распорки:
2 L80x6 Ab
= 2·9.38 = 18.76м2
ix
= 2,47см; Jx
= 147см2
; z0
= 2.19см.

Рис 10 - Усиление колонны распорками из уголков.

2.3 Расчет соединительных планок
Расстояние между центрами тяжести ветвей:
С = bk
– 2z0
= 42 – 2·2.19 = 37.62 см.
Ширина планки в = (0.5 – 0.75)bK
B = 21…31
Принимаем в = 25 см толщина планки
tпл
=(0,1 – 0,4)d, tпл
= 12мм.
Расстояние между центрами планок:

Длина ветви lb
= 97.5 – в =72.5см, что менее ix
[λ] = 2,47·40 = 98,8см.
На ветвь в плоскости планки действует перерезывающая сила, приблизительно равная:
Q = 0.2Ab
= 0.2·18.76 = 3,752кН.
Перерезывающая сила в планке:
 9,7кН. 9,7кН.
Изгибающий момент в планке:
 кНм кНм
Проверяем сварные швы крепления планок к уголкам:
Момент сопротивления сварного шва при катете kf
= 6мм:
WW
=  см2 см2
Нормальные напряжения в шве:

Касательные напряжения в шве:

Проверка приведенных напряжений:
 < Rwf
= 180МПа < Rwf
= 180МПа
Прочность сварных швов обеспечена.
2.4. Расчет ветви распорки на устойчивость при ее предварительном напряжении
Гибкость ветви: 
Условная приведенная гибкость: 
Коэффициент продольного изгиба:
φ = 1 - (0,073 – 5,53 ) )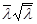 = 1 – (0,073 – 5,53·0,00107)1,45 = 1 – (0,073 – 5,53·0,00107)1,45 0,88 0,88
Величина критических напряжений при потере устойчивости ветви равна:
σкр
= Ry
φ = 220·0.88 = 193.6МПа.
При такой величине напряжений равной γ0
Ry
= 0.9·220 = 198МПа, и определялась требуемая площадь сечения уголков ветви, фактическая площадь имеет запас по сравнению с требуемой. Поэтому можно считать, что уголки не потеряют устойчивость.
Нет необходимости значительно разрушать колонну, поэтому достаточно стальные уголки включать в совместную работу, не создавая в распорках значительных сжимающих напряжений.
Учитывая возможные потери предварительных напряжений при смятии торцов упорных планок в процессе выпрямления распорок σп
= 50МПа, назначаем предварительное напряжение σп
= 100МПа.
2.5 Расчет бокового смещения “Х” в месте изгиба уголков
Величина укорочения при сжатии на полудлине ветви:

0,5l + Δl = 1100 + 0.53 = 1100.53мм.
Боковое смещение:

Так как контролировать такой размер неудобно принимаем Х = 40мм.
При этом изменится напряжение:

0,5l + Δl =  . Δl = 0,72мм . Δl = 0,72мм
Предварительное напряжение:

При создании предварительного напряжения 4 уголка разгружают железобетонную колонну на величину:
N= (σp
– σп
)2Аp
= (134.8 - 50)10-3
·2·18.76·10-4
= 318.2кН.
2.6. Расчет сварных швов крепления планок-упоров к уголкам распорок
Толщина упорных планок принимается равной 15мм. Из условия полного использования прочности сечения уголка на сварные швы передается усилие.
Nш
= Ry
Ay
= 220·9.38·10-1
= 206.4 кН.
Так как из условия размещения сварных швов ширины d=25см упорных планок оказалось недостаточной, принимаем d=30см.
Усилие Nш
с уголка и с дополнительной планки, приваренной в плоскости полки уголка, передается на упорную планку через угловые швы №1 и №2.
Суммарная длина угловых сварных швов №1 и №2:
 4 4
где кf
= 1.2·t = 1.2·0.6 ≈ 7мм.
Расчетная длина шва №2 приходящегося на 1 уголок:
lш2
= 0.5(26-1) = 12.5м
Требуемая длина шва №1: lш1
= lw
- lш2
= 23,4 – 12.5 + 1 = 11,9 cм.
Принимаем шов длиной 12см.
Высота дополнительной планки определяется из условия равнопрочного стыкового шва крепления дополнительной планки к уголку и углового шва №2.
Усилие в шве №2: Nш2
= βf
kf
Rwf
lw
= 0.7·0,7·10-2
·180·103
·12.5·10-2
= 110,3кН
Определяем высоту дополнительной планки из условия работы шва встык на срез:


Рис 13 – К расчету сварных швов.
Список литературы:
1. СНиП 2.01.07-85* Нагрузки и воздействия / Минстрой России. - М.: ГП ЦПП, 1996.-44 с.
2. СНиП 2.03.01-84* Бетонные и железобетонные конструкции / Минстрой России. - М.: ГП ЦПП, 1996. - 76 с.
3. СНиП-II-23-81* Сальные конструкции/ Минстрой России. - М.: ГП ЦПП, 1988. - 94 с.
|