Реферат: Определение среднестатистических показателей
|
Название: Определение среднестатистических показателей Раздел: Рефераты по социологии Тип: реферат | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Задача 17. Определите среднюю урожайность картофеля в регионе по данным о: а) посевной площади и валовом сборе; б) посевной площади и урожайности; в) валовом сборе и урожайности. Объясните, как определена форма средней величины.
а) при определении средней урожайности картофеля в регионе по данным о посевной площади и валовом сборе используем формулу средней арифметической
w (x*f) – валовый сбор; fi – площадь. Х ср =(20550+14840+9810 )/ (139,80+102,34+63,29)= 148 б) по данным по посевной площади и урожайности используем формулу средней арифметической взвешенной:
xi –урожайность по области; fi – посевная площадь по области. Х ср =(139,80*147+102,34*145+63,29*155)/(139,80+102,34+63,29)= 148 в) по данным о валовом сборе и урожайности используем среднюю гармоническую взвешенную:
хi – урожайность; w – валовый сбор. Х ср =(20550+14840+9810 )/(20550/147+14840/145+9810/155) = 148 Задача 27. В целях изучения затрат времени на изготовление одной детали рабочими завода проведена 10%-ная случайная бесповторная выборка, в результате которой получено следующее распределение деталей по затратам времени:
1. На основании этих данных вычислите: средние затраты времени на изготовление одной детали, дисперсию, среднее квадратическое отклонение и коэффициент вариации. 2.С вероятностью 0,954 определить: а) предельную ошибку выборочной средней и возможные границы, в которых ожидаются средние затраты времени на изготовление одной детали на заводе; б) необходимую численность выборочной совокупности, чтобы предельная ошибка выборки при определении средних затрат времени не превышала 1 минуты. Решение: Для расчетов составим таблицу.
1) средние затраты времени на изготовление одной детали рассчитаем по формуле средней арифметической взвешенной, предварительно выбрав середину интервала веса:
Средние затраты времени на изготовление одной детали составили 25,3 мин. 2) дисперсию и среднее квадратическое отклонение рассчитаем по формулам: - дисперсия σ2 = ((xi - xср )2 * fi ) / Σ fi σ2 = 1331/100 =13,31 - среднее квадратическое отклонение σ= √σ2 = √ 13,31 = 3,65 3) коэффициент вариации рассчитаем по формуле ν = σ / хср *100% ν = 3,65/ 25,3 * 100 = 14 (%) ν = 14 % Коэффициент вариации показывает однородность выборки. Если он ниже 35%, выборка однородная, как и в данном случае. 4) Рассчитаем с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидаются средние затраты времени на изготовление одной детали на заводе. Используем для расчета формулу средней ошибки выборочной средней μ х = √ σ2 х /n (1-n/N), где σ2 х – дисперсия изучаемого признака, n- численность выборки, N - число единиц в генеральной совокупности, n/N = 0,1 (десятипроцентное). μ х = √ σ2 х /n (1-n/N) = √13,31/ (100*(1-0,1)) = 0,3 Предельная ошибка выборки рассчитывается по формуле ∆ х = t * μ х , где t – коэффициент доверия, при вероятности 0,954 равен 2 ∆ х = t * μ х = 2*0,3= 0,6 Итак, средние затраты времени на изготовление одной детали находится в пределах хср ±∆ х, или 25,3 ± 0,6 или от 24,7 до 25,9 мин. б) необходимую численность выборочной совокупности, чтобы
n= ( 22 *13,312 *1000) / ( 12 * 1000+22 *13,312 ) = 414 Численность выборочной совокупности, где предельная ошибка выборки при определении средних затрат времени не превышает 1 минуты составит 414 деталей. Задача 37. Имеются данные о среднедушевых доходах населения области за 1993-2002 гг. (тыс. руб.) в сопоставимых ценах:
Требуется выявить основную тенденцию среднедушевых доходов населения области 1993-2002 гг.: 1) методом сглаживания рядов динамики с помощью скользящей трехзвенной средней; 2) методом аналитического выравнивания ряда динамики по уравнению прямой; 3) Используя результаты п.2, дайте прогноз на 2003 год. 4) Охарактеризуйте за 1993-2002 гг. среднегодовой абсолютный прирост и темп прироста доходов. Решение. 1) выявим тенденцию методом сглаживания рядов динамики с помощью скользящей трехзвенной средней по формуле:
2) выявим тенденцию методом аналитического выравнивания ряда динамики по уравнению прямой вида:
Произведем необходимые вычисления в таблице, обозначив время t .
Решим систему уравнений вида:
а∑t+ b ∑t2 = ∑у*t
10 *а +b*55 = 1300 a*55+b*385 =7857 Рассчитаем параметры а, bпо формулам b= а = b =(10*7857-55*1300)/(10*385-55*55)= 8,5697 а = 130-8,5697*5,5 = 82,8667 Рассчитанное уравнение регрессии имеет вид Уt = 82,8667+8,5697*t Для проверки его правильности рассчитаем выравненные значения у. ∑ Представим графически полученные выше расчеты. Прогноз на 2003 год составит: У11 = 82,8667+8,5697*11=177 4) Среднегодовой абсолютный прирост за 1993-2002 гг. рассчитаем по формуле: ∆ср = (Уn-У1 ) / (n-1) ∆ср = (164-100)/9= 7 Среднегодовой темп роста рассчитаем по формуле n -1________ Тр (ср) =√ Yi /Y1 *100% 10 -1________ Тр (ср) =√ 164 /100 *100% = 105,1 Задача 47. Имеются следующие данные:
Рассчитайте: а) индекс физического объема реализации; б) индекс цен и индекс товарооборота. Разложите общую сумму прироста товарооборота по факторам. Сделайте выводы. Вычислим: а) индекс физического объема реализации по формуле
Уpq = (0,5*1500+6300*1,2+2500*2,45)/(1200*0,5+4200*1,2+2000*2,45)= =14435/10540=1,3695 Физический объем реализации увеличился на 36,95 %. б) Индекс цен рассчитаем по формуле Y р = ∑ р0q1*iр / ∑ р0q1 Y р = (0,5*1500*1,01+6300*1,2*0,85+2500*2,45*0,97)/(1500*0,5+6300*1,2+2500*2,45) =13125/14435 = 0,909, или 90,9% В среднем цены снизились на 9,1 %. Индекс товарооборота рассчитаем по формуле
= (0,5*1500*1,01+6300*1,2*0,85+2500*2,45*0,97)/(1200*0,5+4200*1,2+2000*2,45)= = 13125/10540=1,245, или 124,5 % Товарооборот по трем видам увеличился на 24,5 %. Прирост товарооборота всего составил: 13125-10540 = 2585 Изменение за счет увеличения физического объема: 14435-10540=3895 Изменение за счет снижения цен: 13125-14435 = -1310 ИТОГО: 3895-1310 = 2585 Задача 57. Имеются следующие данные о реализации сельскохозяйственных продуктов на колхозных рынках двух городов в сентябре месяце:
1. Для города «А» определите: 1) индекс товарооборота; 2) общий индекс цен на проданные товары (среднее изменение цен); 3) общий индекс физического объема товарооборота (количества Покажите взаимосвязь исчисленных индексов. 2. Для двух городов вместе (по картофелю) вычислите: индекс цен переменного состава (изменение средней цены); индекс цен постоянного состава (среднее изменение цен); индекс структурных сдвигов. Решение: Произведем дополнительные расчеты и представим в таблице
1.1) Индекс товарооборота для города «А» рассчитаем по формуле
Товарооборот по обоим видам в связи с увеличением цен увеличился на 44,1%. 2) общий индекс цен на проданные товары (среднее изменение цен) рассчитаем по формуле Y р = ∑ р1q1 / ∑ р0q1 Y р =1320 /804,4=1,641, или 164,1% В среднем цены увеличились на 64,1 %. 3) общий индекс физического объема товарооборота (количества
В среднем объем снизился на 12,2 %. Взаимосвязь индексов исчисляется: Y рq = Y р * Yq Y рq = 1,641*0,878=1,441 2. Для двух городов вместе (по картофелю) вычислим: Индекс цен переменного состава (изменение средней цены) рассчитаем по формуле Yпер.сост. = ∑ р1 q 1 : ∑ р0 q 0 ∑q1 ∑q0 Yпер.сост. = ((2,5*162+2*300)/(162+300))/ ((1,2*180+0,7*282)/(180+282))=2,431 Индекс цен постоянного состава (среднее изменение цен); Yпост.сост. = ∑ р1 q 1 : ∑ р0 q 1 ∑q1 ∑q1 Yпост.сост. = ((2,5*162+2*300)/(162+300))/ ((1,2*162+0,7*300)/(162+300))=2,485 Индекс структурных сдвигов рассчитаем по формуле Y стр.сдв. = ∑ р0 q 1 : ∑ р0 q 0 ∑q1 ∑q0 Yстр.сост. =((1,2*162+0,7*300)/(162+300))/ ((1,2*180+0,7*282)/(180+282))=0,978 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
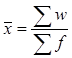
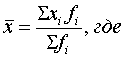
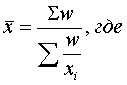
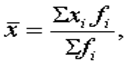
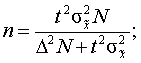
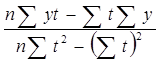
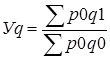 = 1350/1312,5=1,029, или 102,9 %
= 1350/1312,5=1,029, или 102,9 %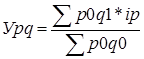
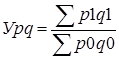 = 1320/916=1,441, или 144,1 %
= 1320/916=1,441, или 144,1 %