Введение
Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Основы этого раздела науки были заложены великими математиками. Назову, например, Ферма, Бернулли, Паскаля. Позднее развитие теории вероятностей определились в работах многих ученых. Большой вклад в теорию вероятностей внесли ученые нашей страны: П.Л.Чебышев, А.М.Ляпунов, А.А.Марков, А.Н.Колмогоров. Вероятностные и статистические методы в настоящее время глубоко проникли в приложения. Они используются в физике, технике, экономке, биологии и медицине. Особенно возросла их роль в связи с развитием вычислительной техники.
Например, для изучения физических явлений производят наблюдения или опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов. Например, повторяя измерения одной и той же величины одним и тем же прибором при сохранении определенных условий (температура, влажность и т.п.), мы получаем результаты, которые хоть немного, но все же отличаются друг от друга. Даже многократные измерения не дают возможности точно предсказать результат следующего измерения. В этом смысле говорят, что результат измерения есть величина случайная. Еще более наглядным примером случайной величины может служить номер выигрышного билета в лотерее. Можно привести много других примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей. Таким образом, теория вероятностей занимается математическим анализом случайных событий и связанных с ними случайных величин.
1. Случайные величины
Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, являются число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д.
Таким образом, случайной величиной называется величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.
Случайные величины можно разделить на две категории.
Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счетное количество значений.
Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.
2. Равномерное распределение
Пусть сегмент оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина  могущая принять любое значение из сегмента могущая принять любое значение из сегмента  . Поэтому . Поэтому 
Если, далее,  и и 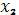 ( (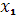 < < ) - две любые отметки на шкале, то согласно условию имеем ) - две любые отметки на шкале, то согласно условию имеем 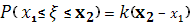
Где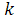 - коэффициент пропорциональности, не зависящий от - коэффициент пропорциональности, не зависящий от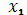 и и , а разность , а разность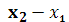 , - длина сегмента , - длина сегмента  . Так как при . Так как при 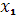 =a и =a и 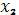 =b имеем =b имеем , то , то 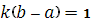 , откуда , откуда  . .
Таким образом
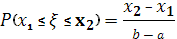 (1) (1)
Теперь легко найти функцию F(x) распределения вероятностей случайной величины  . Если . Если  , то , то 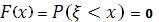
так как не принимает значений, меньших a.
Пусть теперь не принимает значений, меньших a.
Пусть теперь  . По аксиоме сложения вероятностей . По аксиоме сложения вероятностей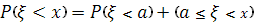 . Согласно формуле (1), в которой принимаем . Согласно формуле (1), в которой принимаем 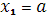 , , 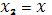 имеем имеем 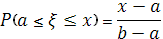
Так как , то при , то при 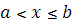 получаем получаем 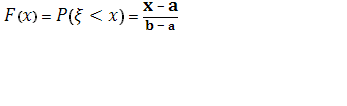
Наконец, если  , то , то 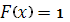 , так как значения , так как значения  лежит на сегменте лежит на сегменте и, следовательно, не превосходят b
. Итак, приходим к следующей функции распределения: и, следовательно, не превосходят b
. Итак, приходим к следующей функции распределения:
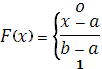
График функции  представлен на рис. 1. представлен на рис. 1.
Плотность распределения вероятностей найдем по формуле. Если 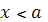 или или  , то , то 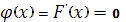 . Если . Если 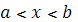 , то , то 
Таким образом,
 (2) (2)
График функции 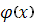 изображен на рис. 2. Заметим, что в точках a
и b
функция изображен на рис. 2. Заметим, что в точках a
и b
функция 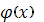 терпит разрыв. терпит разрыв.

Величина, плотность распределения которой задана формулой (2), называется равномерно распределенной случайной величиной.
3. Биномиальное распределение
Биномиальное распределение в теории вероятностей — распределение количества «успехов» в последовательности из n
независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна p
.
Пусть  — конечная последовательность независимых случайных величин с распределением Бернулли, то есть — конечная последовательность независимых случайных величин с распределением Бернулли, то есть 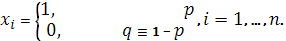
Построим случайную величину Y
:
 . .  . .
Тогда Y
, число единиц (успехов) в последовательности  , имеет биномиальное распределение с n
степенями свободы и вероятностью «успеха» p.
Пишем: , имеет биномиальное распределение с n
степенями свободы и вероятностью «успеха» p.
Пишем:  . Её функция плотности вероятности задаётся формулой: . Её функция плотности вероятности задаётся формулой:

где — биномиальный коэффициент. — биномиальный коэффициент.
Функция распределения биномиального распределения может быть записана в виде суммы:
 , ,
где  обозначает наибольшее целое, не превосходящее число y, или в виде неполной бета-функции: обозначает наибольшее целое, не превосходящее число y, или в виде неполной бета-функции:  . .
Производящая функция моментов биномиального распределения имеет вид:
 , ,
откуда
 , ,
 , ,
а дисперсия случайной величины.
 . .
Свойства биномиального распределения
Пусть  и и . Тогда . Тогда . .
Пусть  и и . Тогда . Тогда . .
Связь с другими распределениями:
Если n
= 1, то, очевидно, получаем распределение Бернулли.
Если n
большое, то в силу центральной предельной теоремы , где N(np,npq)
— нормальное распределение с математическим ожиданием np
и дисперсией npq
. , где N(np,npq)
— нормальное распределение с математическим ожиданием np
и дисперсией npq
.
Если n большое, а λ — фиксированное число, то , где P(λ) — распределение Пуассона с параметром λ. , где P(λ) — распределение Пуассона с параметром λ.
4. Закон Пуассона
Второй предел биноминального распределения, представляющий практический интерес, относится к случаю, когда при неограниченном увеличении числа испытаний математическое ожидание остается постоянным: 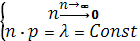
Если при  , , , то перейдя к противоположному событию, мы получим тот же случай. Полагая m << n
, получим при , то перейдя к противоположному событию, мы получим тот же случай. Полагая m << n
, получим при 
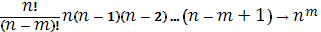
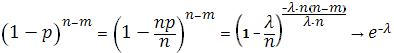
Следовательно,
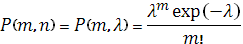
Полученное распределение вероятностей случайной величины называется законом Пуассона.
Распределение Пуассона имеет максимум вблизи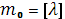
(знак [x]
обозначает целую часть числа x
, меньшую или равную x
).
Числовые характеристики распределения:
Математическое ожидание 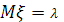
Дисперсия 
Распределение Пуассона играет важную роль для описания "редких" событий в физике, теории связи, теории надежности, теории массового обслуживания и т.д. – там, где в течение определенного времени может происходить случайное число каких-то событий ( радиоактивных распадов, телефонных вызовов, отказов оборудования, несчастных случаев и т.п.).
5.Нормальное распределение
Нормальное распределение – это наиболее важный вид распределения в статистике.
Нормально распределяются значения признака под воздействием множества различных причин, которые практически не взаимосвязаны друг с другом и влияние каждой из которых сравнительно мало, по сравнению с действием всех остальных факторов.
Нормальное распределение отражает вариацию значений признака у единиц однородной совокупности. Подобное распределение наблюдается преимущественно в естественно-научных испытаниях (измерение роста, веса).
В социально-экономических явлениях нормального распределения данные встречаются редко. Здесь всегда присутствуют причины существенным образом влияющие на уровень изучаемого признака (результат управленческого воздействия).
Тем не менее, гипотеза о нормальном распределении исходных данных лежит в основе методологии анализа взаимосвязей выборочного метода и многих других статистических методов.
При достаточно большом числе испытаний нормальная кривая служит пределом, к которому стремятся многие виды распределения, в том числе биномиальное и гипергеометрическое.
Говорят, что случайная величина  нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения  имеет вид имеет вид 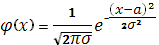 (3) (3)
где a
- любое действительное число, а  >0
. Смысл параметров a
и >0
. Смысл параметров a
и 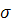 будет установлен в дальнейшем. Исходя из связи между плотностью распределения и функцией распределения будет установлен в дальнейшем. Исходя из связи между плотностью распределения и функцией распределения  , имеем , имеем 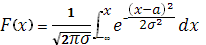
График функции 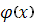 симметричен относительно прямой x=a. Несложные исследования показывают, что функция симметричен относительно прямой x=a. Несложные исследования показывают, что функция 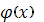 достигает максимума при x=a, а ее график имеет точки перегиба при достигает максимума при x=a, а ее график имеет точки перегиба при 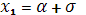 и и 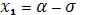 . При . При 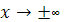 график функции асимптотически приближается к оси Ox. Можно показать, что при увеличении кривая плотности распределения становится более пологой. Наоборот, при уменьшении график плотности распределения сжимается к оси симметрии. При a=0
осью симметрии является ось Oy
. На рис. 3 изображены два графика функции y
= график функции асимптотически приближается к оси Ox. Можно показать, что при увеличении кривая плотности распределения становится более пологой. Наоборот, при уменьшении график плотности распределения сжимается к оси симметрии. При a=0
осью симметрии является ось Oy
. На рис. 3 изображены два графика функции y
=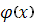 . График I соответствует значениям a
=0, . График I соответствует значениям a
=0,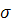 =1, а график II - значениям a
=0, =1, а график II - значениям a
=0, 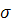 =1/2. =1/2.

Покажем, что функция 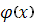 удовлетворяет условию, т.е. при любых a
и удовлетворяет условию, т.е. при любых a
и 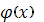 выполняется соотношение выполняется соотношение

В самом деле, сделаем в этом интеграле замену переменной, полагая  . Тогда . Тогда

В силу четности подинтегральной функции имеем

Следовательно,

Но,

В результате получим
 (4) (4)
Найдем вероятность  . По формуле имеем . По формуле имеем 
Сделаем в этом интеграле замену переменной, снова полагая 
Тогда 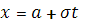 , , 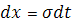 и и
 (5) (5)
Как мы знаем, интеграл  не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (5) вводится функция не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (5) вводится функция  (6) (6)
называемая интегралом вероятностей. Для этой функции составлены таблицы ее значений для различных значений аргумента (см. табл. II Приложения). Используя формулу (6) получим


Итак,
 (7) (7)
Легко показать, что функция Ф(х)
(интеграл вероятностей) обладает следующими свойствами.
1°.
2°.  ; при ; при  величина величина  практически равна 1/2 (см. табл. II). практически равна 1/2 (см. табл. II).
3°.  =-
т.е. интеграл вероятностей является нечетной функцией. =-
т.е. интеграл вероятностей является нечетной функцией.
График функции изображен на рис. 4.

Таким образом, если случайная величина  нормально распределена с параметрами a
и нормально распределена с параметрами a
и 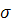 , то вероятность того, что случайная величина удовлетворяет неравенствам , то вероятность того, что случайная величина удовлетворяет неравенствам 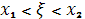 , определяется соотношением (7). , определяется соотношением (7).
Пусть  . Найдем вероятность того, что нормально распределенная случайная величина . Найдем вероятность того, что нормально распределенная случайная величина  отклонится от параметра a по абсолютной величине не более, чем на отклонится от параметра a по абсолютной величине не более, чем на 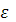 , т.е. , т.е.  . .
Так как неравенство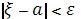 равносильно неравенствам равносильно неравенствам  то полагая в соотношении (7) то полагая в соотношении (7)  , , 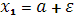 получим получим 
Вследствие того, что интеграл вероятностей - нечетная функция, имеем  (8) (8)
Пример 1. Пусть случайная величина  подчиняется нормальному закону распределения вероятностей с параметрами a=0, подчиняется нормальному закону распределения вероятностей с параметрами a=0, 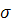 =2. =2.
Определить:
1) 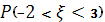 ; ;
2) 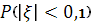 ; ;
Решение:
1) Используя формулу (7), имеем 
Из табл. II находим, что Ф(1)=0,34134
, Ф(1,5)=0,43319.
Следовательно 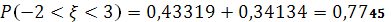 3 3
2) Так как a=0
, то  . По формуле (8) находим . По формуле (8) находим

Пример 2. В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы
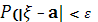 )=0,9973 )=0,9973
Решение: По формуле (8) имеем 
Следовательно, . Из табл. II находим, что этому значению  соответствует =3,откуда соответствует =3,откуда . .
Из последнего примера следует, что если случайная величина подчиняется нормальному закону распределения, то можно утверждать с вероятностью, равной 0,9973
, что случайная величина находится в интервале 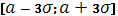 . Так как данная вероятность близка к единице, то можно считать, что значения нормально распределенной случайной величины практически не выходят за границы интервала . Так как данная вероятность близка к единице, то можно считать, что значения нормально распределенной случайной величины практически не выходят за границы интервала  Этот факт называют правилом трех сигм. Этот факт называют правилом трех сигм.
6.Условные законы распределения
Как было показано выше, зная совместный закон распределения можно легко найти законы распределения каждой случайной величины, входящей в систему.
Однако, на практике чаще стоит обратная задача – по известным законам распределения случайных величин найти их совместный закон распределения.
В общем случае эта задача является неразрешимой, т.к. закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами.
Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими.
Все это приводит к необходимости рассмотрения условных законов распределения.
Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение, называется условным законом распределения.
Условный закон распределения можно задавать как функцией распределения так и плотностью распределения.
Условная плотность распределения вычисляется по формулам:


Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины.
Приложение 1
Таблица I: Значения функции:
X
|
 |
X
|
 |
X
|
 |
X
|
 |
| 0.00 |
0.3989 |
1.00 |
0.2420 |
2.00 |
0.0540 |
3.00 |
0.0044 |
| 0.05 |
0.3984 |
1,05 |
0.2299 |
2,05 |
0.0488 |
3,05 |
0.0038 |
| 0.10 |
0.3970 |
1,10 |
0.2179 |
2,10 |
0.0440 |
3,1 |
0.0033 |
| 0.15 |
0.3945 |
1,15 |
0.2059 |
2,15 |
0.0396 |
3,15 |
0.0028 |
| 0.20 |
0.3910 |
1,20 |
0.1942 |
2,20 |
0.0355 |
3,2 |
0.0024 |
| 0.25 |
0.3867 |
1,25 |
0.1826 |
2,25 |
0.0317 |
3,25 |
0.0020 |
| 0.30 |
0.3814 |
1,30 |
0.1714 |
2,30 |
0.0283 |
3,3 |
0.0017 |
| 0.35 |
0.3752 |
1,35 |
0.1604 |
2,35 |
0.0252 |
3,35 |
0.0015 |
| 0.40 |
0.3683 |
1,40 |
0.1497 |
2,40 |
0.0224 |
3,4 |
0.0012 |
| 0.45 |
0.3605 |
1,45 |
0.1394 |
2,45 |
0.0198 |
3,45 |
0.0010 |
| 0.50 |
0.3521 |
1,50 |
0.1295 |
2,50 |
0.0175 |
3,5 |
0.0009 |
| 0.55 |
0.3429 |
1,55 |
0.1200 |
2,55 |
0.0154 |
3,55 |
0.0007 |
| 0.60 |
0.3332 |
1,60 |
0.1109 |
2,60 |
0.0136 |
3,6 |
0.0006 |
| 0.65 |
0.3230 |
1,65 |
0.1023 |
2,65 |
0.0119 |
3,65 |
0.0005 |
| 0.70 |
0.3123 |
1,70 |
0.0940 |
2,70 |
0.0104 |
3,7 |
0.0004 |
| 0.75 |
0.3011 |
1,75 |
0.0863 |
2,75 |
0.0091 |
3,75 |
0.0003 |
| 0.80 |
0.2897 |
1,80 |
0.0790 |
2,80 |
0.0079 |
3,8 |
0.0002 |
| 0.85 |
0.2780 |
1,85 |
0.0721 |
2,85 |
0.0069 |
3,85 |
0.0002 |
| 0.90 |
0.2661 |
1,90 |
0.0656 |
2,90 |
0.0060 |
3,9 |
0.0002 |
| 0.95 |
0.2541 |
1,95 |
0.0596 |
2,95 |
0.0051 |
3,95 |
0.0002 |
| 4.00 |
0.0001 |
Приложение 2
Таблица II: Значения функции
| х |
Ф(х) |
х |
Ф(х) |
х |
Ф(х) |
х |
Ф(х) |
| 0.00 |
0.00000 |
0.85 |
0.30234 |
1,70 |
0.45543 |
2,55 |
0.49461 |
| 0.05 |
0.01994 |
0.90 |
0.31594 |
1,75 |
0.45994 |
2,60 |
0.49534 |
| 0.10 |
0.03983 |
0.95 |
0.32894 |
1,80 |
0.46407 |
2,65 |
0.49598 |
| 0.15 |
0.05962 |
1.00 |
0.34134 |
1,85 |
0.46784 |
2,70 |
0.49653 |
| 0.20 |
0.07926 |
1,05 |
0.35314 |
1,90 |
0.47128 |
2,75 |
0.49702 |
| 0.25 |
0.09871 |
1,10 |
0.36433 |
1,95 |
0.47441 |
2,80 |
0.49744 |
| 0.30 |
0.11791 |
1,15 |
0.37493 |
2,00 |
0.47725 |
2,85 |
0.49781 |
| 0.35 |
0.13683 |
1,20 |
0.38493 |
2,05 |
0.47982 |
2,90 |
0.49813 |
| 0.40 |
0.15542 |
1,25 |
0.39435 |
2,10 |
0.48214 |
2,95 |
0.49841 |
| 0.45 |
0.17364 |
1,30 |
0.40320 |
2,15 |
0.48422 |
3.00 |
0.49865 |
| 0.50 |
0.19146 |
1,35 |
0.41149 |
2,20 |
0.48610 |
3,05 |
0.49931 |
| 0.55 |
0.20884 |
1,40 |
0.41924 |
2,25 |
0.48778 |
3,10 |
0.49966 |
| 0.60 |
0.22575 |
1,45 |
0.42647 |
2,30 |
0.48928 |
3,15 |
0.499841 |
| 0.65 |
0.24215 |
1,50 |
0.43319 |
2,35 |
0.49061 |
3,20 |
0.499928 |
| 0.70 |
0.25804 |
1,55 |
0.43943 |
2,40 |
0.49180 |
3,25 |
0.499968 |
| 0.75 |
0.27337 |
1,60 |
0.44520 |
2,45 |
0.49286 |
3,40 |
0.499997 |
| 0.80 |
0.28814 |
1,65 |
0.45053 |
2,50 |
0.49379 |
3,45 |
0.5 |
|