ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра прикладной математики
КУРСОВАЯ РАБОТА
по дисциплине: «Математическое моделирование»
на тему: «Применение теоремы о среднем для исследования
функции привлечения клиентов банка»
Выполнил: студент
группы ПМ-06-2
Сысоев А.С.
________________
«___»______2009 г.
Проверил: д.ф.-м.н., профессор
Блюмин С.Л.
________________
________________
«___»______2009 г.
Липецк – 2009
|
О Г Л А В Л Е Н И Е
ВВЕДЕНИЕ. 2
1.ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ.. 4
2.ЭЛАСТИЧНОСТЬ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ.. 6
3.АЛЬТЕРНАТИВНЫЕ ФОРМЫ ИЗМЕНЕНИЯ ВЕЛИЧИНЫ.. 8
4.ТЕОРЕМА О СРЕДНЕМ ЛАГРАНЖА.. 9
5.НЕКОТОРЫЕ НЕКЛАССИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ.. 11
ТЕОРЕМЫ ЛАГРАНЖА.. 11
6.ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ КОББА-ДУГЛАСА.. 14
7.ФУНКЦИЯ, ОПИСЫВАЮЩАЯ РЕЗУЛЬТАТЫ РАБОТЫ.. 17
СТРУКТУРЫ ПО ПРИВЛЕЧЕНИЮ КЛИЕНТОВ БАНКА.. 17
ЗАКЛЮЧЕНИЕ. РЕЗЮМЕ. 19
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ. 20
Моделирование процесса любой сферы деятельности, будь то экономика или производство, начинается с построения качественной модели. Мы исходим из того, что модель имеет право на существование, если она опирается на накопленные знания, надежные достоверные источники, отражает главные характеристики изучаемого объекта и дает новые знания о нем.
Результатом длительного сбора интересующей информации и тщательного ее анализа является построение именно качественной математической модели. Одним из возможных вариантов такой модели может служить производственная функция. В зависимости от числа факторов, входящих в модель, различают однофакторные и многофакторные производственные функции.
Построением и исследованием экономико-математических моделей, описывающих влияние факторов на результирующий показатель, и оценкой оказываемого этими факторами влияния занимается экономический факторный анализ [1].
Долгое время в экономическом анализе не было формулы, отражающей точную связь между изменениями экономического показателя и факторов, оказывающих на него влияние. Однако из математического анализа такая зависимость давно известна как формула конечных приращений (теорема о промежуточной точке) Лагранжа. Она устанавливает точное равенство между приращениями функции и аргумента. В контексте экономического факторного анализа теорема Лагранжа о среднем как раз и устанавливает связь между экономическим показателем и факторами.
В рамках университетского курса теорема Лагранжа изучается в привычной аддитивной форме, т.е. в виде зависимости между приращениями
функции и аргументов. Однако рассмотрение других «неклассических» форм изменения экономико-математических величин позволяет получить некоторые другие «неклассические» формы представления формулы конечных приращений Лагранжа.
1. ПРОИЗВОДСТВЕННЫЕ ФУНКЦИИ
В наиболее простом случае производство продукции (или благ) обусловлено только одним фактором. В этом случае п
роизводственная функция –
это функция, независимая переменная которой принимает значения используемого ресурса (фактора производства), а зависимая переменная – значения объемов выпускаемой продукции или услуг:
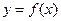 . .
В этой формуле y
есть функция одной переменной x
. В связи с этим производственная функция (ПФ) называется одноресурсной или однофакторной. Ее область определения – множество неотрицательных действительных чисел. Однако математическое обозначение 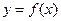 в контексте экономики не совсем корректно. Отклик может определяться и некоторым другим распределением ресурсов между структурными единицами экономики. В этом случае ПФ – статистически устойчивая связь между затратами ресурса и выпуском. Тогда более правильной является символика: в контексте экономики не совсем корректно. Отклик может определяться и некоторым другим распределением ресурсов между структурными единицами экономики. В этом случае ПФ – статистически устойчивая связь между затратами ресурса и выпуском. Тогда более правильной является символика:

где а
– некий параметр ПФ.
Производственная функция нескольких переменных
– это функция, независимые переменные которой принимают значения объемов затрачиваемых или используемых ресурсов (число переменных n
равно числу ресурсов), а значение функции имеет смысл величин объемов выпуска:
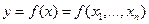 . .
В этой формуле 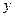 ( ( ) – скалярная, а х
– векторная величина, x
1
,…,х
n
-координаты вектора х
, то есть ) – скалярная, а х
– векторная величина, x
1
,…,х
n
-координаты вектора х
, то есть 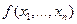 есть числовая функция нескольких переменных x
1
,…,х
n
. В связи с этим ПФ есть числовая функция нескольких переменных x
1
,…,х
n
. В связи с этим ПФ 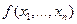 называют многоресурсной или многофакторной. Более правильной является такая символика называют многоресурсной или многофакторной. Более правильной является такая символика  где а
– вектор параметров ПФ. где а
– вектор параметров ПФ.
Считается, что производственная функция дифференцируема и обладает следующими свойствами [4]:
1. Если 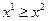 , то , то  . Это означает, что увеличение любого вида затрат не приводит к уменьшению выпуска продукции. . Это означает, что увеличение любого вида затрат не приводит к уменьшению выпуска продукции.
2. Если отсутствует хотя бы один необходимый фактор производства, т.е.  , то выпуск продукции (производство благ) невозможен: , то выпуск продукции (производство благ) невозможен:  . Так, например, при отсутствии основных фондов выпуск продукции равен нулю. . Так, например, при отсутствии основных фондов выпуск продукции равен нулю.
3. Функция 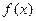 предполагается строго вогнутой, т.е. ее матрица Гессе Н
является отрицательно определенной. предполагается строго вогнутой, т.е. ее матрица Гессе Н
является отрицательно определенной.
Однако применяемые в экономике конкретные производственные функции не всегда обладают всеми указанными свойствами.
2. ЭЛАСТИЧНОСТЬ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ
Все экономические или технологические показатели можно разделить на абсолютные и относительные. Первые относятся к категории объёмных, так как при их вычислении используется непосредственная оценка. Вторые, относительные показатели, относятся к типу удельных и представляют собой отношения абсолютных (или других относительных) показателей, то есть количество единиц одного показателя на одну единицу другого. Относительными показателями являются не только соотношения разных показателей в один и тот же момент времени, но и одного и того же, но в разные моменты; это темпы роста (индексы) данного показателя. В экономическом анализе и принятии решений в одних случаях важны абсолютные показатели (например, общий объём прибыли или суммарный объём производства), в других – относительные (например, доход на душу населения или удельные показатели энергоёмкости).
Основная задача экономического факторного анализа заключается в получении факторного разложения приращения результирующего показателя в виде некоторой его зависимости от абсолютных приращений факторов модели.
Одним из примеров относительных показателей является коэффициент эластичности, который показывает относительное изменение исследуемого показателя под действием некоторого единичного относительного изменения фактора, от которого он зависит, при неизменных остальных влияющих на него факторах.
В общем случае, предельной (точечной) эластичностью [5] производственной функции 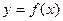 называется предел отношения относительных изменений показателя y
и переменной (фактора) x
. Обозначив эластичность изменения функции y
при изменении фактора x
через называется предел отношения относительных изменений показателя y
и переменной (фактора) x
. Обозначив эластичность изменения функции y
при изменении фактора x
через  , получаем: , получаем:
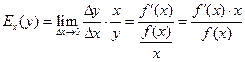 . .
3. АЛЬТЕРНАТИВНЫЕ ФОРМЫ ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
В классической математике изменение любой величины принято рассматривать в форме приращения, т.е. разности — со знаком или без (по модулю) в зависимости от ставящейся задачи. Но почему бы не рассмотреть изменение величины в такой форме, как отношение — например, конечного значения к начальному и т.д. [6]
Итак, пусть задана какая-то величина. Тогда, в качестве ее начального значения примем a
, в качестве конечного - b
. Изменение этой величины может быть охарактеризовано, по меньшей мере, тремя способами:
1) разность (отклонение, приращение):  ; ;
2) частное (индекс):  ; ;
3) относительное приращение: 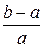 . .
Модель зависимости экономического показателя 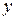 от влияющего на него фактора от влияющего на него фактора 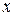 может быть представлена производственной функцией может быть представлена производственной функцией 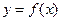 . Тогда, очевидно, что при изменении фактора . Тогда, очевидно, что при изменении фактора 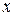 от от  до до 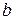 , изменяется и показатель , изменяется и показатель 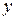 - от - от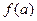 до до  . [6] . [6]
В классическом математическом анализе существует формула, определяющая зависимость изменения функции (экономического показателя 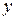 ) от изменения аргумента (влияющего фактора ) от изменения аргумента (влияющего фактора 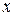 ). Эта формула широко известна как теорема о среднем Лагранжа, или формула конечных приращений. ). Эта формула широко известна как теорема о среднем Лагранжа, или формула конечных приращений.
4. ТЕОРЕМА О СРЕДНЕМ ЛАГРАНЖА
Теорема о среднем дифференциального исчисления (формула конечных приращений Лагранжа)
. Если функция  непрерывна на отрезке непрерывна на отрезке 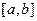 и дифференцируема во всех внутренних точках этого отрезка, то внутри и дифференцируема во всех внутренних точках этого отрезка, то внутри 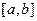 найдется точка найдется точка 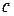 такая, что справедлива формула [3] такая, что справедлива формула [3]
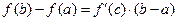 . (1) . (1)
Доказательство
. Рассмотрим на отрезке 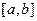 следующую вспомогательную функцию следующую вспомогательную функцию
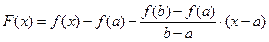 . (1.1) . (1.1)
Проверим, что для функции 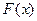 выполнены все условия теоремы Ролля. В самом деле, выполнены все условия теоремы Ролля. В самом деле, 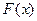 непрерывна на отрезке непрерывна на отрезке 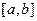 (как разность функции (как разность функции  и линейной функции) и во всех внутренних точках отрезка и линейной функции) и во всех внутренних точках отрезка 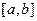 имеет производную, равную имеет производную, равную
 . .
Из формулы (1.1) очевидно, что  . .
Согласно теореме Ролля внутри отрезка 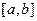 найдется точка найдется точка 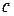 такая, что такая, что
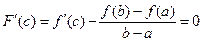 . (1.2) . (1.2)
Из равенства (1.2) вытекает формула Лагранжа (1).
Геометрическая интерпретация теоремы Лагранжа приведена на рис. 3. Заметим, что 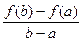 является угловым коэффициентом секущей, проходящей через точки является угловым коэффициентом секущей, проходящей через точки  , ,  кривой y
= f
(x
), а кривой y
= f
(x
), а 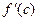 есть угловой коэффициент касательной к той же кривой, проходящий через точку есть угловой коэффициент касательной к той же кривой, проходящий через точку 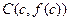 . .
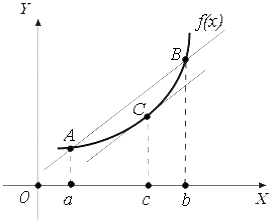
Рис. 3. Графическая интерпретация теоремы Лагранжа.
Из теоремы Лагранжа следует, что на кривой y
= f
(x
) между точками A
и B
найдется такая точка C
, касательная в которой параллельна секущей AB
.
Доказанная формула 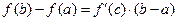 носит название формулы Лагранжа или формулы конечных приращений
. Она очевидно верна и для случая носит название формулы Лагранжа или формулы конечных приращений
. Она очевидно верна и для случая  . .
5. НЕКОТОРЫЕ НЕКЛАССИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ
ТЕОРЕМЫ ЛАГРАНЖА
В связи с предположением о существовании альтернативных форм изменения математической величины встает задача получения зависимостей, связывающих изменения функции и аргументов, подобно теореме Лагранжа о среднем для приращений. Получение таких зависимостей базируется на классической теореме Лагранжа.
Получим зависимость индекса функции от индекса аргумента. Пусть задана зависимость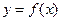 . Тогда . Тогда 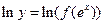 . Рассмотрим логарифм индекса аргумента . Рассмотрим логарифм индекса аргумента  . Аналогично для индекса функции . Аналогично для индекса функции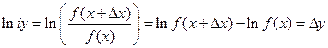
Теорема о среднем в знакомой нам всем форме имеет вид  . .
А теорема Лагранжа, в которой разности заменены частными (индексами)  . Имеем . Имеем  , где , где  - производная, выраженная через частные. - производная, выраженная через частные.
Классически производная определяется следующим образом  . .
Введем замену  , ,  . Предположим, что переменные . Предположим, что переменные  и и  положительны. Пусть положительны. Пусть  , ,  . При этом . При этом 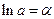 , ,  , ,  , ,  , ,  . Операция логарифмирования переводит частные в разности: . Операция логарифмирования переводит частные в разности: 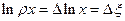 , , 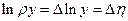 . .
Производная преобразованной функции имеет вид [3] 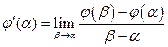 , причем , причем 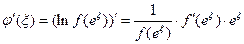 . .
После возврата к исходным переменным имеем
 , ,
тогда 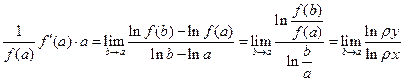 . .
После окончательного возврата к исходным переменным имеем 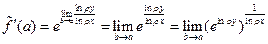   . Полученное выражение является определением производной, выраженной через частные. . Полученное выражение является определением производной, выраженной через частные.
Тогда теорема Лагранжа примет вид:
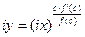 . (2) . (2)
Рассматривая различные формы изменения величины, указанные выше, можно получить еще семь разных зависимостей, представляющих собой формулу конечных приращений Лагранжа (подобно мультипликативной, индексной зависимости) [6]:
- зависимость индекса функции от приращения аргумента:
 , (3) , (3)
- зависимость индекса функции от относительного приращения аргумента:
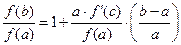 ,(4)
,(4)
- зависимость приращения функции от индекса аргумента:
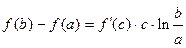 ,
(5) ,
(5)
- зависимость приращения функции от относительного приращения аргумента:
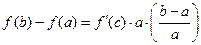 , (6)
, (6)
- зависимость относительного приращения функции от приращения аргумента:
 , (7)
, (7)
- зависимость относительного приращения функции от индекса аргумента:
 , (8) , (8)
- зависимость относительного приращения функции от относительного приращения аргумента:
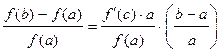 . (9)
. (9)
6. ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ КОББА-ДУГЛАСА
Трудно себе представить, что такой сложный объект как экономика целой страны можно было описать функцией, имеющей простое аналитическое выражение. В 1928 г. американские экономисты К.У. Кобб и П.Х. Дуглас для описания состояния экономики того периода предложили следующую функцию:
 (10) (10)
Функция Кобба-Дугласа есть частный случай многофакторной ПФ. Откликом этой модели является объем выпуска ресурсов, а факторами – трудовые ресурсы ( ) и производственные фонды ( ) и производственные фонды (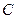 ). Параметры – A
и ). Параметры – A
и 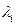 . В частности
. В частности 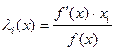 - частные эластичности факторов, коэффициенты пропорциональности между изменениями величины показателя (функции) и фактора (аргумента), влияющего на этот показатель в краткосрочном периоде времени.
- частные эластичности факторов, коэффициенты пропорциональности между изменениями величины показателя (функции) и фактора (аргумента), влияющего на этот показатель в краткосрочном периоде времени.
До настоящего времени функция Кобба-Дугласа наряду с некоторыми другими широко используется для приближения производственных функций различных объектов. В более общем случае функцией Кобба-Дугласа называют функцию:
 . .
Одним из вариантов построения ПФ Кобба-Дугласа является рассмотрение ее как уравнения множественной регрессии.
Уравнение множественной регрессии имеет вид:
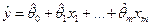 , (11) , (11)
где 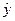 - выход (результирующий показатель), - выход (результирующий показатель),  - факторы, - факторы,  - коэффициента уравнения, которые находятся по формуле: - коэффициента уравнения, которые находятся по формуле: 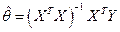 . .
При логарифмировании выражения (10) получаем: 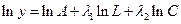 или или
 . (12) . (12)
Сравнивая (11) и (12), приходим к выводу, что (12) – типичное уравнение множественной регрессии, в котором в качестве выхода имеем логарифм результирующего показателя, а в качестве входов – логарифмы значений 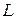 (трудовые ресурсы) и (трудовые ресурсы) и  (производственные фонды) [7]. (производственные фонды) [7].
Так как модель (10) не является линейной зависимостью, то для её построения нельзя применить метод наименьших квадратов (МНК). Но, если линеаризовать (12), то, возможно, используя МНК, рассчитать коэффициенты множественной регрессии (по сути, частные эластичности степенной ПФ).
Проверка качества построенной зависимости включает в себя следующие этапы [2]:
- проверку статистической значимости коэффициентов уравнения (на основе t-статистики),
- проверку общего качества уравнения регрессии (используя коэффициент детерминации 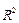 ), ),
- проверку свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполнимости предпосылок МНК).
Если после проведенной проверки нет оснований отвергать построенную линейную зависимость, то возможен переход обратно к нелинейному уравнению степенной ПФ (10). Такой переход основан на применении действий, обратных логарифмированию.
7. ФУНКЦИЯ, ОПИСЫВАЮЩАЯ РЕЗУЛЬТАТЫ РАБОТЫ
СТРУКТУРЫ ПО ПРИВЛЕЧЕНИЮ КЛИЕНТОВ БАНКА
В отделе, занимающемся работой по привлечению клиентов, одного из крупных Липецких банков была получена модель, описывающая выполнение плана по проработке клиентов текущего квартала и некоторыми контрольными показателями предыдущего квартала. Такими показателями являлись величины среднедневных остатков, объем оборотов, полученных в результате эквайринговых операций, оборот средств в иностранной валюте и доходы, полученные от инкассации.
Полученная зависимость – аддитивная форма ПФ Кобба-Дугласа – построена как уравнение множественной регрессии и является достаточно качественной для описания указанного экономического процесса.
ПФ результатов привлечения клиентов банка имеет вид:
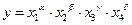 , (13) , (13)
где  - РКО (расчетно-кассовое обслуживание, контрольный показатель – величины среднедневных остатков в национальной валюте), - РКО (расчетно-кассовое обслуживание, контрольный показатель – величины среднедневных остатков в национальной валюте),
 - ВЭД (внешнеэкономическая деятельность, контрольный показатель – величины среднедневных остатков в иностранной валюте), - ВЭД (внешнеэкономическая деятельность, контрольный показатель – величины среднедневных остатков в иностранной валюте),
 - ЭКВГ (эквайринговые операции, контрольный показатель – объемы денежных средств, полученных от эквайринговых операций), - ЭКВГ (эквайринговые операции, контрольный показатель – объемы денежных средств, полученных от эквайринговых операций),
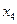 - ИНКАСС (инкассация, контрольный показатель – объемы денежных средств, полученных от предоставления услуг инкассаторов). - ИНКАСС (инкассация, контрольный показатель – объемы денежных средств, полученных от предоставления услуг инкассаторов).
Построение такой модели позволяет значительно упростить планирование выполнения нормативов, устанавливаемых головным отделением банка.
Модель (13) построена на основе методов математической статистики с использованием операций логарифмирования и обратных к ним. Это говорит о стохастическом характере
модели.
Сбор информации идет по окончании отчетного периода отдела банка (месячный отчет), следовательно, мы каждый месяц имеем новые значения вектора входной информации. Значит, модель (13) – дискретная
. По структуре модель является статической
.
Параметры модели 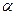 , , 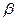 , ,  и и 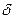 , по своей сути – частные эластичности факторов, вычисляемые по формулам , по своей сути – частные эластичности факторов, вычисляемые по формулам 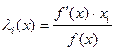 (при условии, что известна промежуточная точка
(при условии, что известна промежуточная точка 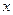 ). Следовательно, можно сделать вывод, что модель (13) линейна по параметрам
. ). Следовательно, можно сделать вывод, что модель (13) линейна по параметрам
.
В работе рассмотрены основные понятия, касающиеся производственных функций, в частности, рассмотрен один из относительных показателей, характеризующих ПФ – эластичность. Сделано предположение о существования неких форм изменения математической величины, отличных от приращения, а именно индекса и относительного приращения. В связи с этим решена задача получения зависимостей для изменения указанных форм изменения значений функции от изменений аргументов. Полученные зависимости представляют собой неклассические формы записи теоремы о среднем (формулы конечных приращений) Лагранжа. С использованием аппарата математической статистики и эконометрик построена модель, описывающая результаты работы банковской структуры, занимающейся работой по привлечению новых клиентов.
Использование формул, полученных в пункте «Некоторые неклассические представления теоремы Лагранжа» значительно упрощает расчет и планирование банком уменьшения или увеличения проработка какого-либо конкретного контрольного показателя для управления общим планом проработки клиентов.
Например, теорема Лагранжа для индексов показателя и факторов для описанной модели примет вид:
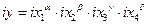 . .
Получение нужной формы записи теоремы о среднем для рассмотренной модели (производственной функции) производится аналогично.
1. Блюмин С. Л., Суханов В. Ф., Чеботарёв С. В. Экономический факторный анализ: Монография. – Липецк: ЛЭГИ, 2004. – 148 с.
2. Бородич С.А. Вводный курс эконометрики: Учебное пособие – Мн.: БГУ, 2000. – 354 с.
3. Математический анализ: учеб. / В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов; под ред. А. Н. Тихонова. – 3-е изд., перераб. и доп.: в 2 ч. Ч. 1. – М.: ТК Велби, Изд-во Проспект, 2006. – 672 с.
4. Минюк С.А. Математические методы и модели в экономике: Учеб. пособие / Минюк С.А., Ровба Е.А., Кузьмич К.К. – Мн.: ТетраСистемс, 2002. – 432 с.
5. Солодовников А. С., Бабайцев В. А., Браилов А. В., Шандра И. Г. Математика в экономике: Учеб., Ч. 2. М.: Финансы и статистика, 2001. – 376 с.
6. Сысоев А.С. Об одной теореме классического математического анализа / VI Всероссийская школа-семинар молодых ученых «Управление большими системами»: Сборник трудов. – Т1. – Ижевск: ООО Информационно-издательский центр «Бон Анца», 2009. – 400 с.
7. Сысоев А.С., Блюмин С.Л. Построение производственной функции Кобба-Дугласа как эмпирического уравнения множественной регрессии // Сборник тезисов докладов Студенческой научно-технической конференции Липецкого государственного технического университета. – Липецк: ЛГТУ, 2009 г.
|