Лабораторная работа: Исследование движения тел в диссипативной среде 2

Министерство Образования РФ

Санкт-Петербург

Государственный Электротехнический Университет “ЛЭТИ”

Кафедра физики

Исследование движения тел в диссипативной среде

Лабораторная работа N1

Санкт-Петербург

2004

Исследуемые закономерности

Сила сопротивления движению в вязкой среде. В вязкой среде на движущееся тело действует сила сопротивления, направленная против скорости тела. Эта сила обусловлена вязким трением между слоями среды и пропорциональна скорости тела

,

где v – скорость движения тела, r – коэффициент сопротивления, зависящий от формы, размеров тела и от вязкости среды h.

Для шара радиуса R коэффициент сопротивления определяется формулой Стокса

При движении тела в вязкой среде происходит рассеяние (диссипация) его кинетической энергии. Слой жидкости, находящийся в непосредственной близости от поверхности движущегося тела, имеет ту же скорость, что и тело, по мере удаления скорость частиц жидкости уменьшается. В этом состоит явление вязкого трения, в результате которого энергия тела передается слоям окружающей среды в направлении, перпендикулярном движению тела.

Слой жидкости, находящийся в непосредственной близости от поверхности движущегося тела, имеет ту же скорость, что и тело, по мере удаления скорость частиц жидкости уменьшается. В этом состоит явление вязкого трения, в результате которого энергия тела передается слоям окружающей среды в направлении, перпендикулярном движению тела.

Движение тела в диссипативной среде. Движение тела массой m под действием постоянной силы F при наличии сопротивления среды описывается следующим уравнением:

.

В данной работе тело движется под действием силы тяжести, уменьшенной в результате действия выталкивающей силы Архимеда, т.е.

,

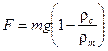где r_с и r_т – плотности среды и тела, соответственно. Таким образом, уравнение движения преобразуется к виду

.

Если начальная скорость движения тела равна нулю, то равна нулю и сила сопротивления, поэтому начальное ускорение

.

С увеличением скорости сила сопротивления возрастает, ускорение уменьшается, обращаясь в нуль. Дальше тело движется равномерно с установившейся скоростью v _¥ .Аналитическое решение уравнения движения при нулевой начальной скорости выражается формулой

,

где t - время релаксации. Соответствующая зависимость скорости движения тела в диссипативной среде от времени представлена на рис. 2.

где h – высота расположения тела над дном сосуда

Передача энергии жидкой среде, окружающей движущееся тело, происходит за счет совершения работы против сил трения. Энергия при этом превращается в тепло, идет процесс диссипации энергии. Скорость диссипации энергии (мощность потерь) в установившемся режиме

.

Учитывая, что m / t = r , получим уравнение баланса энергии на участке установившегося движения

Рис. 2

.

Указания по выполнению наблюдений

1. Масштабной линейкой измерить расстояние Dh между средней и нижней меткой на боковой поверхности сосуда.
2. На аналитических весах взвесить поочередно 5 шариков, и записать массу каждого шарика в таблицу Протокола наблюдений.
3. Поочередно опуская шарики в жидкость через впускной патрубок, измерить секундомером время прохождения каждым шариком расстояния между двумя метками на боковой поверхности сосуда. Результаты записать в таблицу Протокола наблюдений.
4. На панели макета установки указаны значения плотности жидкости в сосуде и плотности материала шариков. Эти данные также следует записать в Протокол наблюдений.

Задание на подготовку к работе

1. Выполните индивидуальное домашнее задание №2
2. Изучите описание лабораторной работы.
3. Выведите формулу для определения коэффициента сопротивления r , полагая что известно значение установившейся скорости v _¥ . Выведите также формулу погрешности Dr .
4. Выведите формулу для определения коэффициента вязкости h на основе рассчитанного коэффициент сопротивления r , массы и плотности материала шариков.
5. Подготовьте бланк Протокола наблюдений, основываясь на содержании раздела «Указания по проведению наблюдений». Разработайте и занесите в бланк Протокола наблюдений таблицу результатов наблюдений.

Задание по обработке результатов

1. По данным таблицы результатов наблюдений определите значения установившихся скоростей шариков. Рассчитайте значения коэффициентов сопротивления r для каждого опыта.
2. Определите коэффициент вязкости h исследуемой жидкости. Найдите его среднее значения и погрешность полученного результата.
3. Промежуточные вычисления и окончательные результаты, полученные в п. 1, 2 сведите в таблицу.
4. Для одного из опытов определите мощность рассеяния и проверьте баланс энергии на участке установившегося движения.
5. Также для одного из опытов найдите время релаксации t, постройте графики скорости и ускорения от времени.

Результаты, полученные в п. 3 и 4, следует округлить, основываясь на значениях погрешностей величин, рассчитанных ранее.

Министерство Образования РФ

Санкт-Петербург

Государственный Электротехнический Университет “ЛЭТИ”

Кафедра физики

ОТЧЕТ

по лабораторно-практической работе № 1

ИССЛЕДОВАНИЕ

ДВИЖЕНИЯ ТЕЛ В ДИССИПАТИВНОЙ СРЕДЕ

Выполнил Чистяков А.О.

Факультет РТ

Группа № 4121

Преподаватель Дедык А.И.

«Выполнено» «____» ___________

Подпись преподавателя __________

ПРОТОКОЛ НАБЛЮДЕНИЙ

ЛАБОРАТОРНАЯ РАБОТА №1

ИССЛЕДОВАНИЕ

ДВИЖЕНИЯ ТЕЛ В ДИССИПАТИВНОЙ СРЕДЕ

Таблица 1

Измеряемая величина	Номер наблюдения
	1	2	3	4	5
	206
	136	119	90	89	80
t (сек)	5,45	5,55	7,1	7,15	7,75
	0,038	0,037	0,029	0,029	0,027

Выполнил Чистяков А.О.

Факультет РТ

Группа № 4121

«1» октября 2004

Преподаватель Дедык А.И.

Обработка результатов

1.По полученным данным рассчитываем скорость движения V_∞ для каждого шарика.

Формула для расчета скорости движения , где

Δh – расстояние между метками,

t – время прохождения шариком расстояния Δh между метками в сосуде.

1.1 Рассчитываем диаметр и радиус каждого шарика.

Пусть – объем шарика, в – диаметр шарика, R – радиус шарика, тогда

теперь приравниваем и получаем формулы для расчета диаметра и радиуса шариков;

1.2 Вычислим коэффициент вязкости исследуемой жидкости, для каждого из опытов

2. Упорядочим ; проверим на промахи; найдем и ;

N	1	2	3	4	5
	1,095	1,162	1,163	1,173	1,175
	119	89	90	80	136
t (сек)	5,55	7,15	7,1	7,75	5,45
	206

R– размах выборки

U_{p 1 n} =0,64; N=5; P≈95%

Из этого видно что промах поэтому

исключаем его из таблицы. Теперь таблица

выглядит так:

N	1	2	3	4
	1,162	1,163	1,173	1,175
	89	90	80	136
t (сек)	7,15	7,1	7,75	5,45
	2,5	2,5	2,4	2,8
	206

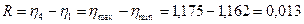
2.1 Теперь находим среднее значение

2.2 Находим среднеквадратическое отклонение результатов измерения

2.3 Найдем средний квадрат отклонения

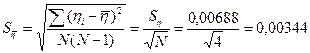
2.4 Высчитаем случайную погрешность результатов измерений

=0,72; =3,2 ;N=4; P≈95%

I.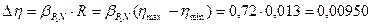

II.

2.5 Производим вывод выражений для частных производных от функции

rdf

2.6 По каждому набору совместно измеренных значений аргументов и их приборных погрешностей рассчитаем приборную погрешность функции

2.7 Вычислить среднюю приборную погрешность функции

2.8 Вычисляем полную погрешность функции

2.9 Запишем результат измерения и округлим его

3. Рассчитайте значения коэффициентов сопротивления r для каждого опыта

Для шара радиуса R коэффициент сопротивления определяется формулой Стокса

4. Определим время релаксации. Предположим, что скорость прохождения шарика между слоями равна постоянной скорости (скорости равномерного падения шарика), то есть

ν_i =ν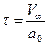_¥ ; где

Время релаксации t_i очень мало, поэтому шарики до прохождения первой отметки успевают принять постоянную скорость ν_¥ , т.е. их движение является установившимся на пути от верхней метки к нижней.

5. Определим мощность рассеяния для каждого шарика

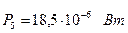
6. Графики

См. в конце на миллиметровке

7. Сведем все данные в таблицу

	113	114				112		120			117
	0.5*
t (сек)	5.86	5.87				5.85		5.37			5.45
	0.5*
	200
	0.5*
	0,03413	0,03407				0,03419		0,03724			0,03670
	1,161	1,169				1,1531		1,1092			1,1055	1,1396
	0,003918
	1,162		1,163				1,173			1,175
	0,001				0,01				0,002
	-0,006			-0,005			0,005			0,006		SDi = 0
(Di )2	36∙ 10-6			25∙ 10-6			25∙ 10-6			36∙ 10-6		S(Dfi )2 =122 ∙ 10-6
	0,03555			0,03550			0,03657			0,03393

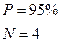
8. Упорядочим ; проверим на промахи; найдем и ;

N	1	2	3	4	5
	0,0262	0,0269	0,0271	0,028	0,0314
	80	89	90	119	136
t (сек)	7,75	7,15	7,1	5,55	5,45
	206

R– размах выборки

U_{p 1 n} =0,64; N=5; P≈95%

Из этого видно что промах поэтому исключаем его из таблицы. Теперь таблица выглядит так:

N	1	2	3	4
	0,0262	0,0269	0,0271	0,028
	80	89	90	119
t (сек)	7,75	7,15	7,1	5,55
	206

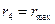
2.1 Теперь находим среднее значение

2.2 Находим среднеквадратическое отклонение результатов измерения

2.3 Найдем средний квадрат отклонения

2.4 Высчитаем случайную погрешность результатов измерений

=0,72; =3,2 ;N=4; P≈95%

I.

II.

2.5 Производим вывод выражений для частных производных от функции

2.6 По каждому набору совместно измеренных значений аргументов и их приборных погрешностей рассчитаем приборную погрешность функции

2.7 Вычислить среднюю приборную погрешность функции

2.8 Вычисляем полную погрешность функции

2.9 Запишем результат измерения и округлим его

Вывод: Коэффициент вязкости () полученный и рассчитанный в ходе лабораторных измерений отличается от стандартного значения, в основном из-за погрешностей, допущенных в ходе измерения массы шарика и времени прохождения им между двумя отметками. Для более точного измерения нам необходим электронный секундомер.