Контрольная работа: Решение задачи с помощью программ Mathcad и Matlab Моделирование движения

Контрольная работа

Решение задачи с помощью программ Mathcad и MatLab

Содержание

Задание

1. Теоретический расчет формул

2. Программа в Matchad

3. Программа в Matlab

Выводы по работе

Задание

Легкая заряженная частица падает вертикально вниз (под влиянием силы тяжести) на одноименно заряженную пластину (начальная скорость обеспечивает движение вниз независимо от соотношения силы тяжести и силы отталкивания). Промоделировать движение частиц, считая поле, созданное пластиной однородным.

Исходные данные:

a) m=10^(-3);

b) q=10^(-9);

c) qp=10^-6);

d) r₀ =1;

e) ε₀ =8,85*10^(-12);

f) ε=1;

g) g=9,8.

1. Теоретический расчет формул

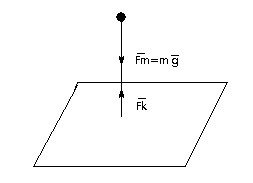
Рис. 1. Частица падает на пластину

Данная частица меняет свою высоту над пластиной и скорость движения в 2 случаях:

1. Частица падает на пластину под влиянием силы тяжести. Высота rменяется по закону: r =r0+ν₀₁ *t+(g*t^2)/2 . Так как ν₀₁ =0, то r=r0 – (g*t^2)/2. Подлетая к пластине на эту частицу действует отталкивающая сила, равная силе Кулона F_k =(q_пл *q)/(4*π*ε₀ *ε*r^2). В какой-то момент t₀ скорость частицы будет равна 0, т.е. она «повиснет в воздухе», ее результирующая сила также равна 0: F=F_k +F_m =0. => (q_пл *q)/(4*π*ε₀ *ε*r^2)=mg =>

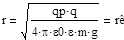
r - - минимальное значение высоты,на которое падает частица

Скорость меняется по закону:

ν(t)=ν0+dr/dt=2*r0/t–g*t

2. Частица отталкивается от пластины под влиянием силы Кулона. Высота меняется по закону:

r =rк+ν₀₂ *t+(а*t^2)/2. Так как ν₀₂ =0, получим:

.

Скорость менятся по закону: ν(t)=dr/dt

2. Программа в Mathcad

Исходные данные:

Результаты расчетов:

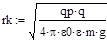
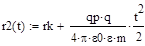
Задано:

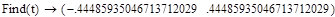
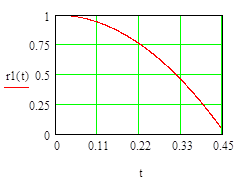
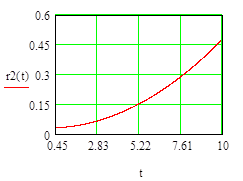
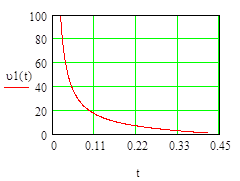
3. Программа в Matlab

m=10^(-3);

q=10^(-9);

qp=10^(-6);

r0=1;

e0=8.85*10^(-12);

e=1;

g=9.8;

rk=sqrt((qp*q)/4*pi*e0*e*m*g);

t1=[0:0.08:0.48];

r1=r0-(g*t1.^2)./2

subplot(2,2,1);plot(t1,r1)

grid on

xlabel('t')

ylabel('r1')

v1=r0./t1-g.*t1

subplot(2,2,2);plot(t1,v1)

grid on

xlabel('t')

ylabel('v1')

t2=[0.5:1:6.5];

r2=rk+((qp*q)/(4*pi*e0*e*m)).*(t2.^2)./2

subplot(2,2,3);plot(t2,r2)

grid on

xlabel('t')

ylabel('r2')

v2=((qp*q)/(4*pi*e0*e*m)).*t2

subplot(2,2,4);plot(t2,v2)

grid on

xlabel('t')

ylabel('v2')

Результат:

Выводы по работе

Данная задача была решена с помощью двух программ: Mathcad и MatLab. Были построены зависимости высоты, на которой находится точка, от времени и скорости движения этой частицы от времени. Были построены 4 графика: первые 2 – это случай, когда частица падает вниз, а 2 других – частица оттолкнулась от данной пластины. В первом случае высота rуменьшается под действием силы тяжести от некоторого значения r₀ до какого-то конечного значения r_k . Скорость также уменьшается, так как на нее действует сила Кулона. Она «тормозит» данную частицу. При каком-то значении t₀ сила Кулона становится равной силе тяжести, а затем и больше нее по модулю, поэтому частица отталкивается и летит вверх по той же траектории (в идеальном случае). Значение rувеличивается, скорость также увеличивается.