Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Филиал государственного образовательного учреждения высшего профессионального образования
ВСЕРОССИЙСКОГО ЗАОЧНОГО
ФИНАНСОВО – ЭКОНОМИЧЕСКОГО ИНСТИТУТА
в г. Брянске
ЛАБОРАТОРНАЯ РАБОТА
по дисциплине
ЭКОНОМЕТРИКА
| ВЫПОЛНИЛ(А) |
Зятева М.В.
|
| СТУДЕНТ(КА) |
3 курса, «день»
|
| СПЕЦИАЛЬНОСТЬ |
Финансы и кредит
|
| № ЗАЧ. КНИЖКИ |
08ффб00876
|
| ПРЕПОДАВАТЕЛЬ |
Малашенко В.М.
|
Брянск — 2011
ВАРИАНТ 6
Имеются данные о продаже квартир на вторичном рынке жилья в Санкт-Петербурге на 01.05.2000 г. .
Таблица 6
| № п/п
|
Y
|
X
1
|
X
2
|
X
3
|
X
4
|
Х
5
|
X
6
|
X
7
|
| 1 |
13,0 |
1 |
1 |
37,0 |
21,5 |
6,5 |
0 |
20 |
| 2 |
16,5 |
1 |
1 |
60,0 |
27,0 |
22,4 |
0 |
10 |
| ……………………………………………………………………………………. |
| 76 |
43,0 |
4 |
0 |
110,0 |
79,5 |
10,0 |
0 |
5 |
Принятые в таблице обозначения:
· Y
— цена квартиры, тыс. долл.;
· X
1
— число комнат в квартире;
· X
2
— район города (1 — центральные, 0 — периферийные);
· X
3
— общая площадь квартиры (м2
);
· X
4
— жилая площадь квартиры (м2
);
· X
5
— площадь кухни (м2
);
· X
6
— тип дома (1 — кирпичный, 0 — другой);
· X
7
— расстояние от метро, минут пешком.
Требуется:
1. Составить матрицу парных коэффициентов корреляции между всеми исследуемыми переменными и выявить коллинеарные факторы.
2. Построить уравнение регрессии, не содержащее коллинеарных факторов. Проверить статистическую значимость уравнения и его коэффициентов.
3. Построить уравнение регрессии, содержащее только статистически значимые и информативные факторы. Проверить статистическую значимость уравнения и его коэффициентов.
Пункты 4 — 6 относятся к уравнению регрессии, построенному при выполнении пункта 3.
4. Оценить качество и точность уравнения регрессии.
5. Дать экономическую интерпретацию коэффициентов уравнения регрессии и сравнительную оценку силы влияния факторов на результативную переменную Y
.
6. Рассчитать прогнозное значение результативной переменной Y
, если прогнозные значения факторов составят 75 % от своих максимальных значений. Построить доверительный интервал прогноза фактического значения Y
c надежностью 80 %.
Решение.
Для решения задачи используется табличный процессор EXCEL.
1. С помощью надстройки «Анализ данных
… Корреляция
» строим матрицу парных коэффициентов корреляции междувсеми исследуемыми переменными (меню «Сервис
» ® «Анализ данных
…» ® «Корреляция
»). На рис. 1
изображена панель корреляционного анализа с заполненными полями[1]
. Результаты корреляционного анализа приведены в прил. 2
и перенесены в табл. 1
.

р
ис. 1. Панель корреляционного анализа
Таблица 1
Матрица парных коэффициентов корреляции
| № п/п
|
Y
|
X1
|
X2
|
X3
|
X4
|
Х5
|
X6
|
X7
|
| № п/п |
1 |
| Y |
0,659028 |
1 |
| X1 |
0,963382 |
0,701543 |
1 |
| X2 |
-0,31659 |
-0,04533 |
-0,15567 |
1 |
| X3 |
0,749439 |
0,902307 |
0,800467 |
-0,00025 |
1 |
| X4 |
0,811817 |
0,886429 |
0,849104 |
-0,04782 |
0,968772 |
1 |
| Х5 |
0,160024 |
0,530689 |
0,251822 |
0,137106 |
0,612691 |
0,437911 |
1 |
| X6 |
-0,22163 |
-0,18695 |
-0,26421 |
-0,13562 |
-0,25952 |
-0,29348 |
-0,05625 |
1 |
| X7 |
-0,13427 |
-0,07244 |
-0,11142 |
-0,00122 |
-0,02316 |
-0,08252 |
0,192753 |
0,215595 |
1 |
Для построения уравнения регрессии значения используемых переменных (Y
,X
2
, X
3
, X
4
, X
5
, X
6
) скопируем на чистый рабочий лист (прил. 3)
. Уравнение регрессии строим с помощью надстройки «Анализ данных… Регрессия
»(меню «Сервис»
® «Анализ данных…
» ® «Регрессия
»). Панель регрессионного анализа с заполненными полями изображена на рис. 2
.
Результаты регрессионного анализа приведены в прил. 4
. Уравнение регрессии имеет вид
Y=0,66+0,96х-0,32х+0,75х+0,81х+0,16х-0,22х-0,14х
Уравнение регрессии признается статистически значимым, так как вероятность его случайного формирования в том виде, в котором оно получено, составляет 1,11×10-23
что существенно ниже принятого уровня значимости a=0,05.

р
ис.
2. Панель регрессионного анализа модели
Y
(Х,
X
2
,
X
3
,
X
4
,
X
5
,
X
6,
,Х)
3. По результатам проверки статистической значимости коэффициентов уравнения регрессии, проведенной в предыдущем пункте, строим новую регрессионную модель, содержащую только информативные факторы, к которым относятся:
· факторы, коэффициенты при которых статистически значимы;
· факторы, у коэффициентов которых t
‑статистика превышает по модулю единицу (другими словами, абсолютная величина коэффициента больше его стандартной ошибки).
Для построения уравнения регрессии скопируем на чистый рабочий лист значения используемых переменных (прил. 5)
и проведем регрессионный анализ (рис. 3
). Его результаты приведены в прил. 6
и перенесены в табл. 3
. Уравнение регрессии имеет вид:
Y=1,9-1,59х-1,08х+0,26х+0,22х+0,05х+1,57х-0,13х

р
ис. 3. Панель регрессионного анализа модели
Y
(Х,
X
2
,
X
3
,
X
4
,
X
6
,Х)
4. Оценим качество и точность последнего уравнения регрессии, используя некоторые статистические характеристики, полученные в ходе регрессионного анализа (см.
«Регрессионную статистику
»):
· множественный коэффициент детерминации

показывает, что регрессионная модель объясняет 83 % вариации цены квартиры Y
.
· стандартная ошибка регрессии
 тыс. руб. тыс. руб.
показывает, что предсказанные уравнением регрессии значения годовой прибыли Y
отличаются от фактических значений в среднем на 237,6 тыс. руб.
Средняя относительная ошибка аппроксимации определяется по приближенной формуле:
 , ,
где  тыс. руб. — среднее значение цены квартиры (определено с помощью встроенной функции «СРЗНАЧ
»; прил. 1
). тыс. руб. — среднее значение цены квартиры (определено с помощью встроенной функции «СРЗНАЧ
»; прил. 1
).
Е
отн
показывает, что предсказанные уравнением регрессии значения годовой прибыли Y
отличаются от фактических значений в среднем на 16,7 %. Модель имеет удовлетворительную точность (при  — точность модели высокая, при — точность модели высокая, при  — хорошая, при — хорошая, при  — удовлетворительная, при — удовлетворительная, при 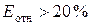 — неудовлетворительная). — неудовлетворительная).
5. Для экономической интерпретации коэффициентов уравнения регрессии сведем в таблицу средние значения и стандартные отклонения переменныхв исходных данных (табл. 4
)
. Средние значения были определены с помощью встроенной функции «СРЗНАЧ
», стандартные отклонения — с помощью встроенной функции «СТАНДОТКЛОН
» (см. прил. 1
).
| Переменная
|
Y
|
X
2
|
X
3
|
X
4
|
X
6
|
| Среднее |
25,09
|
0,395
|
71,05
|
45,40
|
0,382
|
| Стандартное отклонение |
12,08
|
0,492
|
30,28
|
21,80
|
0,489
|
1) Фактор
X
2
(район города)
Средний коэффициент эластичности фактораX
2
имеет значение
 . .
Он показывает, что с изменением района города цена меняется на 0,02 %.
2) Фактор
X
3
(общая площадь квартиры)
Средний коэффициент эластичности фактораX
3
имеет значение
 . .
Он показывает, что при увеличении общей площади квартиры на 1м цена квартиры увеличивается в среднем на 0,74%.
3) Фактор
X
4
(Жилая площадь квартиры)
Средний коэффициент эластичности фактораX
4
имеет значение
 . .
Он показывает, что при увеличении жилой площади квартиры на 1м цена квартиры увеличивается в среднем на 0,4 %.
|