| Расчет гидродинамической системы
1 ПОСТАНОВКА ЗАДАЧИ
Определить расход и потерю давления в гидравлической системе. По трубам (гидравлически гладким) движется жидкость при давлении 0,4 МПа и температуре 300 К. Размеры элементов системы приведены в табл.1. Расходная характеристика нагнетательного элемента, является зависимостью величины расхода от перепада давлений на элементе и задана зависимостью  . .
Рис.1. Схема гидравлической системы. Таблица.1. Размеры элементов системы
| №
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
| L, м
|
1,0
|
1,5
|
0,5
|
1,0
|
2,0
|
1,0
|
1,5
|
1,5
|
0,8
|
1,0
|
1,8
|
0,7
|
| d, м
|
0,02
|
0,02
|
0,02
|
0,016
|
0,016
|
0,025
|
0,02
|
0,02
|
0,02
|
0,025
|
0,02
|
0,015
|
| R, м
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
0,7
|
-
|
-
|
2 ПОСЛЕДОВАТЕЛЬНОСТЬ РасчетА гидродинамической системы
Необходимо определить расход в гидравлической системе, при известном перепаде давления DР.
Для решения применяется графоаналитический метод. При решении задачи, изменяем величину расхода, определяя соответствующие величины перепада давления, и строим график зависимости ΔР=f
(G
). Используя величину перепада давления, находим, используя график, соответствующий расход G
.
2.1 Считая, что давление в системе практически не изменяется, из уравнения состояния идеального газа определим плотность жидкости: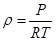
2.2 Используя формулу Сазерленда, определим динамическую и кинематическую вязкость воздуха:
 ; ;  . .
2.3 Зададим расход в системе G. И предположим, что в трубопроводе в параллельной и боковой ветви расходы соответственно равны  и и  , где k
–коэффициент разделения потока. , где k
–коэффициент разделения потока.
2.4 Выразим коэффициенты гидравлического сопротивления для всех элементов в параллельных участках. Для участка параллельной ветви это гидравлические сопротивления трения труб 7, 8 а также местные гидравлические сопротивления прямых проходов приточного тройника и вытяжного тройника и повороты потока. Коэффициенты гидравлического сопротивления трения выражаются через величину расхода в канале (k
*
G
или (1-k
)*G
), а также гидравлический диаметр канала. Определяем суммарные потери давления для каждой ветви по формуле Дарси-Вейсбаха. Так как все геометрические размеры системы известны, то величина потерь давления является функцией заданной величины расхода и неизвестного коэффициента разделения потока k
. Найдем корень уравнения, обеспечивающий равенство потерь давлений в параллельных каналах, определим коэффициент разделения потока.
2.5 Определим коэффициенты гидравлических потерь и сами потери для неразветвленной части системы: потери на трение в трубах, а также местные потери при повороте потока. Определим суммарные потери давления в гидравлической системе.
2.6 Изменяя величину расхода, произведем расчеты. Результаты расчетов сведём в таблицу.
2.7 По результатам расчетов построим графики ΔP(G), ΔP(Gv
) рис.2.
2.8 Определяем точку пересечения, которая и будет определять искомые результаты.
3 РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
Таблица 2. Падение давления на различных элементах системы
| G, м^3/с
|
ΔP1,
Па
|
ΔP2
, Па
|
ΔP3
, Па
|
ΔP4
, Па
|
ΔP5
, Па
|
ΔP6
, Па
|
ΔP9
, Па
|
ΔP1
0
, Па
|
ΔP11
, Па
|
| 0.0004
|
6.6
|
9.9
|
3.3
|
19.2
|
38.4
|
2.3
|
5.3
|
2.3
|
11.9
|
| 0.0008
|
22.3
|
33.5
|
11.1
|
64.5
|
129.1
|
7.7
|
17.9
|
6.4
|
40.
|
| 0.0012
|
45.4
|
68.2
|
22.7
|
131.3
|
262.6
|
15.7
|
36.4
|
11.9
|
81.9
|
| 0.0016
|
75.2
|
112.9
|
37.6
|
217.2
|
434.5
|
26
|
60.2
|
18.7
|
135.5
|
| 0.002
|
111.2
|
166.8
|
55.6
|
321
|
642
|
38.5
|
88.9
|
26.4
|
202
|
| 0.0024
|
153
|
229
|
76
|
441
|
883
|
53
|
122
|
35
|
275
|
| G, м^3/с
|
ΔPb
, Па
|
ΔP21
, Па
|
ΔP45
, Па
|
k
|
| 0.0004
|
9.2
|
10.7
|
26.3
|
0,633
|
| 0.0008
|
33.2
|
43.1
|
105.3
|
0.656
|
| 0.0012
|
68.1
|
97.1
|
237
|
0.657
|
| 0.0016
|
113.4
|
172.6
|
421.4
|
0.658
|
| 0.002
|
168.3
|
269.7
|
658.5
|
0.659
|
| 0.0024
|
232
|
948
|
388
|
0.659
|

Рис.2. График зависимостей потерь давления в системе и перепада давления на нагнетательном элементе от величины расхода.
В системе установится расход 0.002 m^3/c, и падение давления 3812 Па.
По результатам расчета параметров гидравлической системы расчитаем площади поперечных сечений для всех участков, местное сопротивление, коэффициенты. сопротивления трения для гладких труб.
Исходные данными при этом являются:
 
  
  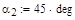
  
 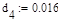 
 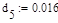 
 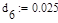
 
 
 
 
 
 

 Давление Давление
 Температура Температура
 Газовая постоянная Газовая постоянная
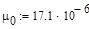 Вязкость при T=273 K Вязкость при T=273 K
 Константа Сазерленда Константа Сазерленда
Придерживаясь вышеуказанной последовательности, находим площади поперечных сечений для всех участков:


Найдём плотность потока вязкость при Т=300К ,
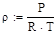 
 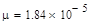
  Вязкость при Т=300 Вязкость при Т=300
Зададим расход:

 Скорости в n-тых участках Скорости в n-тых участках
 число Рейнольдса в n-тых участках число Рейнольдса в n-тых участках
 
Найдём коэффициенты. сопротивления трения для гладких труб:


 Проверим условие (Ro/d)>3.При выполнении условия, сопротивление изогнутого участка найдём по формуле: Проверим условие (Ro/d)>3.При выполнении условия, сопротивление изогнутого участка найдём по формуле:
 
Находим местные сопротивления для:
1. Приточный тройник
Выразим расход в боковой и прямой ветвях.


Местное сопротивление бокового ответвления приточного тройника :

Местное сопротивление бокового ответвления приточного тройника формула, где к - коэффициент разделения потока.

Местное сопротивление прямого протока приточного тройника:

Определим коэффициент

Местное сопротивление прямого протока приточного тройника определяем по формуле:

2. Вытяжной тройник
Местное сопротивление бокового ответвления вытяжного тройника:
Определим коэффициент А
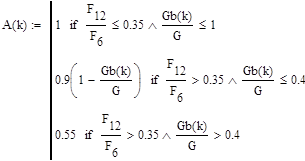
Местное сопротивление бокового ответвления вытяжного тройника формула:

Местное сопротивление прямого протока вытяжного тройника :
Определим коэффициент K':

Местное сопротивление прямого протока вытяжного тройника:

3. Местные сопротивления колен:
 
 
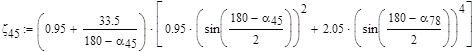 
4. Местные сопротивления на резких расширениях и сужениях канала:

Найдём падение давления в параллельных участках :
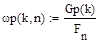
Скорость в прямой ветви в n-тых участках

Рейнольдс в прямой ветви в n-тых участках


Скорость в боковой ветви в n-тых участках:


Рейнольс в боковой ветви в n-тых участках
Падение давления в прямой ветви
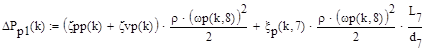
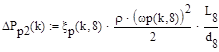

Падение давления в боковой ветви

Из условия  = = найдем к - коэффициент разделения: найдем к - коэффициент разделения:



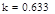 коэффициент разделения при данном расходе коэффициент разделения при данном расходе
Падение давления в параллельных участках
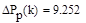

Падение давления на всей системе.
местные потери давления

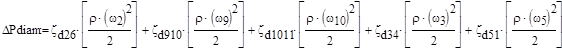

  
Определение равновесного состояния падения давления и расхода.
Вектор X - значения расхода, при которых были вычислены Y n-тые (падение давления)

Создадим интерполяционную функцию P(G) по точкам Y






Найдем расход при котором установится равновесие.



Определим падение давления при данном расходе

Ответ : В системе установится расход 0.002 m^3/c, и падение давления 3812 Па.
Список литературы
1. Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. Пер. с нем. – М.: Мир, 2005.- 512с.
2. Хоровиц П., Хилл У. Азбука схемотехники. –М.:Мир, 2001.-598с.
3. Тули М. Справочное пособие по цифровой электронике: Пер. с англ. – М.: Энергоатомиздат, 1999.- 176с.
4. Карлащук В.И. Электронная лаборатория на IBM-PC.- М.: Солон, 2006.- 512с.
5. Костиков В.Г. Источники питания электронных средств. Схемотехника и конструирование: Учебник для вузов.-2-е изд.—М.: Горячая линия - Телеком, 2008.- 344с.: ил.
|